基于吸收态马尔可夫链的概率与期望问题
楼思远
(杭州第十四中学,浙江 杭州 310006)

然而,有些问题从上述常规的角度出发很难找到突破口,如2019年全国数学高考Ⅰ卷理科试题的第21题(概率递推)、2023年全国数学新高考Ⅰ卷的第21题(期望递推)等,这类问题以概率论与统计学中著名的马尔可夫链模型为背景,需通过分析建立各个状态之间的递推关系,然后结合数列的相关知识与技巧才能顺利求解.因此,对师生而言,了解并掌握马尔可夫链模型是很有必要的.本文主要介绍马尔可夫链中有关吸收态模型的概念,并探讨以其为背景命制的相关问题的解答思路与技巧.
马尔可夫链是一组具有马尔可夫性质的离散随机变量的集合,具体定义如下:
按照系统的发展,时间离散化为n=0,1,2,….对每一个n,系统的状态用随机变量Xn表示,记ai=P(Xn=i)为i时刻的状态概率,pij=P(Xn+1=j|Xn=i)为从Xn=i过渡到Xn+1=j的转移概率,若Xn+1状态下的条件概率仅依赖前一状态Xn的取值及其转移概率,而与Xn-1,Xn-2,…的取值无关(无后效性),即
P(Xn+1|…Xn-2Xn-1Xn)=P(Xn+1|Xn),
则称序列X={Xn:n>0}为马尔可夫链.
马尔可夫链是描述随机动态过程的重要模型之一,它包含了吸收态这一重要模型,利用这个模型可快速求解中学阶段一些复杂的概率与期望问题.
1 吸收态模型的定义
定义[1]称转移概率为pij=1的状态i为吸收状态.若一个有k种状态的马尔可夫链至少包含一个吸收状态,且从任意非吸收状态出发,经过有限次转移都能以大于0的概率到达某个吸收状态,则称之为吸收态(一旦进入吸收态,则不会再逃离这一状态).

下面通过两道例题来说明上述模型的具体应用.
(2023年浙江省杭州市高三年级第二次教学质量检测数学试卷第21题改编)
分析赌徒输光或者赌金达到预期的B元,赌徒才会停止赌博,因此这二者为吸收态,而其余情况皆为非吸收态,非吸收态最终将到达吸收态.同时,只有目前赌徒剩余的赌金会影响到下一次赌金的所有状态时,才满足吸收态模型.
解根据分析,作出状态转移图如图1所示,由图列出状态转移方程:
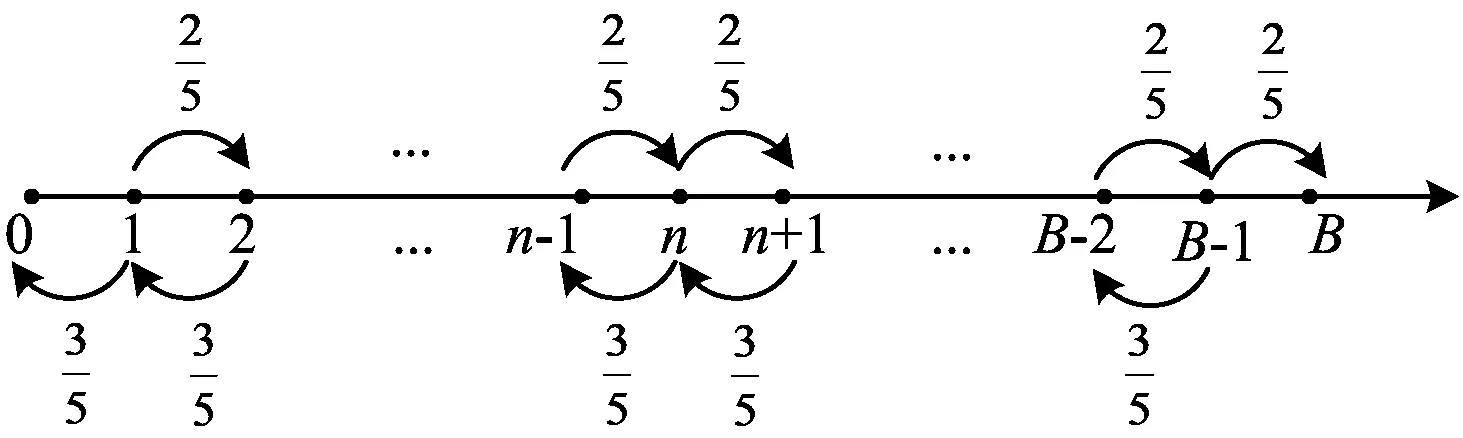
图1

注意到p(0)=1,p(B)=0,由特征根法可得
例2一只蚂蚁在单位立方体上以每秒一个单位的速度沿棱运动,它从任一顶点开始运动.假设每次蚂蚁到达顶点后转向各方向继续运动的概率相同(允许向后转折返走动),则其第一次重返起点所需时间的数学期望为多少?
(2023年浙江省数学夏令营测试卷第19题)
分析画出单位立方体如图2所示,不妨设蚂蚁从点A出发,求其第一次返回点A所需时间的期望.根据立方体的对称性,经过分析可知:从起点A(记为A类)出发将等可能地走到点B1,B2,B3三者之一,将这三点记为B类;从B类出发将回到A类,或者等可能地走到点C1,C2,C3三者之一,将这三点记为C类;从C类出发将等可能地回到B类各点,或者到达点D(记为D类);从D类出发将等可能地回到C类各点.显然A类为吸收态,其余各类皆为非吸收态,非吸收态最终将到达吸收态.同时,只有蚂蚁目前所处的位置会影响到下一次的位置状态,满足吸收态模型.

图2
解根据分析,令E1,E2,E3和E4分别表示从A类、B类、C类和D类出发重返A类所需时间的期望.作出状态转移图如图3所示,由图列出状态转移方程:

图3
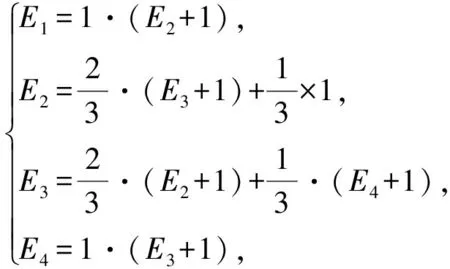
解得E1=8,故蚂蚁第一次重返起点所需时间的数学期望为8秒.
上述两个问题最终归结为在吸收态马尔可夫链模型下求解.该模型的主要解题步骤为:寻找前后状态的转移关系,作出状态转移图,利用全概率公式列出状态转移方程,建立对应的递推关系.其中,明确题目中概率或期望的含义,厘清前后状态的转移关系是解决问题的关键.
2 模型的拓展应用
例3如图4,在平面直角坐标系内有一个正方形,它包含了25个整点.一个粒子从原点(0,0)出发,每过一秒钟,它都以相同的概率移动到最接近其当前位置的8个整点中的一个,即粒子从(x,y)等概率地移动到(x,y+1),(x+1,y+1),(x+1,y),(x+1,y-1),(x,y-1),(x-1,y-1),(x-1,y),(x-1,y+1)其中之一,当粒子碰到正方形边缘上的整点时,马上停止移动.试问:当粒子停止移动时,它位于4个角(点A,B,C,D)之一的概率是多少?

图4
解根据对称性以及转移状态的概率情况,把这25个整点分为5类:
a类:(0,0);b类:(-1,0),(0,-1),(1,0),(0,1);c类:(-1,-1),(-1,1),(1,-1),(1,1);d类:A,B,C,D;e类:正方体边缘除去A,B,C,D的整点.并记P1为a→d的概率,P2为b→d的概率,P3为c→d的概率,P4为d→d的概率,P5为e→d的概率.作出状态转移图(如图5)并列出状态转移方程:

图5

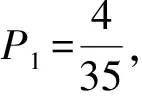
评注对整点进行归类,设定相应的概率表示是解题的关键,其中P4和P5对应的状态为吸收态.
例4一只蚂蚱在直角坐标平面内位于y≥0的区域上跳来跳去,寻找位于水平线y=24上的河流.蚂蚱每跳一次,就随机选择一个与坐标轴平行的方向,并向该方向移动一个单位.当蚂蚱在y=0的某一点时,它会以相同的可能性选择3个方向中的一个跳跃.若蚂蚱从点(0,21)开始寻找,一旦到达河边的某一点就会停止.试问:蚂蚱到达河边所需跳跃次数的期望是多少?
解令E(y0)表示当蚂蚱从水平线y=y0的某个位置出发,最终到达河边的跳跃次数的期望值,作出状态转移图(如图6)并列出状态转移方程:
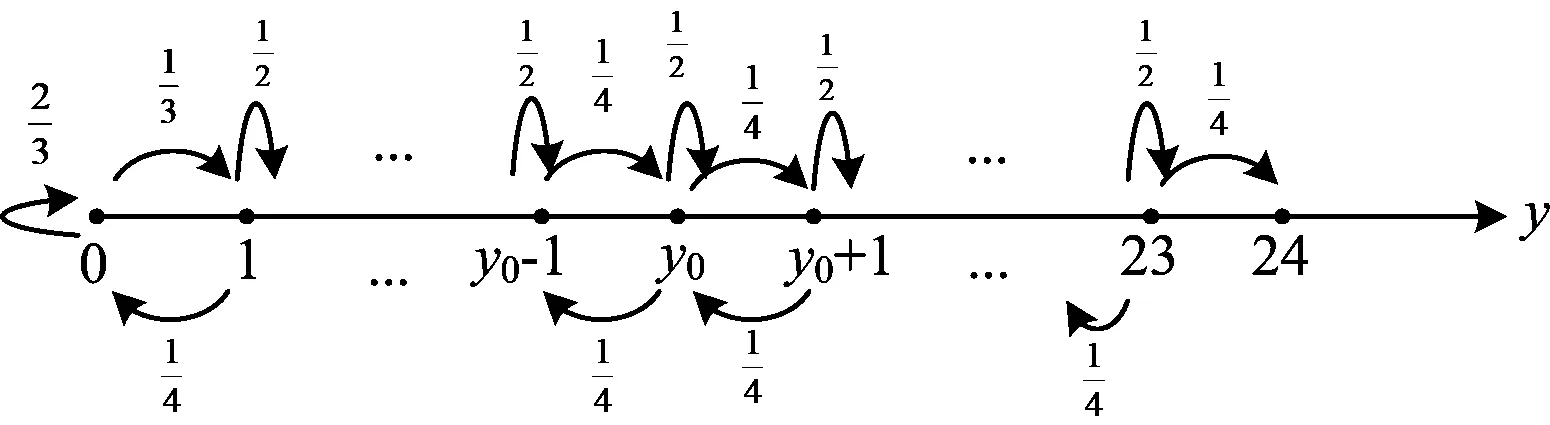
图6
化简得
注意到E(24)=0,代入上式迭代得E(21)=273,故蚂蚱到达河边所需跳跃次数的期望是273次.
评注对前后状态的关系讨论是关键,其中E(24)对应的状态为吸收态.
例5设A1A2A3…A12为一个正十二边形(如图7),有3只兔子最初分别位于顶点A4,A8和A12处,每过1分钟,3只兔子同时随机、独立地跳到与其当前位置相邻的两个顶点中的一个.一旦有2只兔子跳到了同一个顶点,则3只兔子同时停止跳跃.试问:当兔子停止跳跃时,跳跃时间的分钟数的期望是多少?
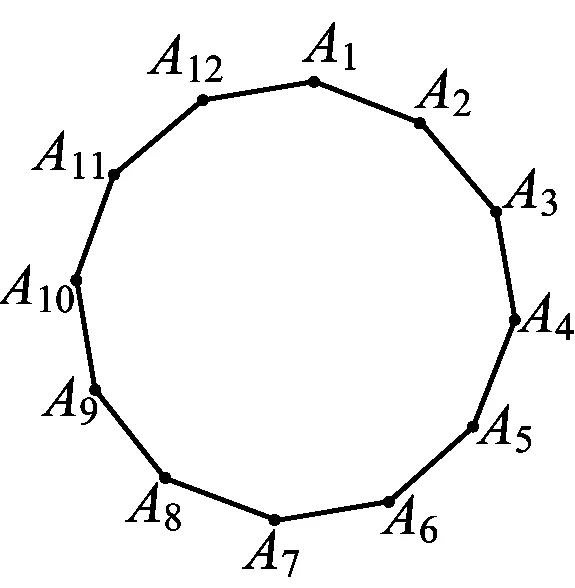
图7
解在停止跳跃前,如果不考虑顺序,那么3只兔子之间的距离状态(指不包含第3只兔子的距离)只有(4,4,4),(2,4,6),(2,2,8)这3种情况;而在停止跳跃时,距离状态只能是(0,x,y)(其中x,y∈N+)这一种情况.分别记a类:(4,4,4);b类:(2,4,6);c类:(2,2,8);d类:(0,x,y).并记E1为a→d的分钟数期望,E2为b→d的分钟数期望,E3为c→d的分钟数期望,E4为d→d的分钟数期望.作出状态转移图(如图8)并列出状态转移方程:

图8
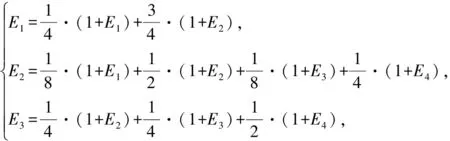
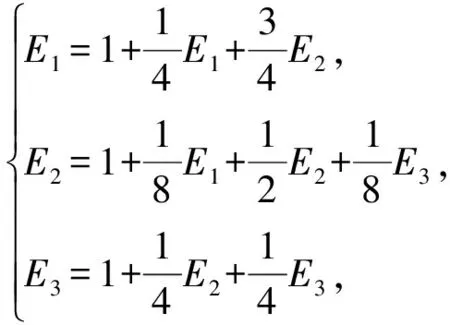

评注定义兔子之间的距离状态是此题的本质与核心,其中E4对应的状态为吸收态.
例6袋中共有m+n个小球,其中红球m个,蓝球n个,除了颜色之外各球完全相同.现每次从袋中随机取出1个小球,若为红球则放回袋中;若为蓝球则不放回,直到取出所有的蓝球为止,求取球次数的期望.
解当袋中有s(其中s≤n)个蓝球时,记最终取完所有蓝球的取球次数期望为Es.注意到红球个数m始终保持不变,作出状态转移图(如图9)并列出状态转移方程:

图9


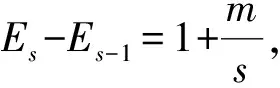
评注从蓝球个数的变化状态入手进行讨论,其中E0对应的状态为吸收态.
3 研究模型的意义
在人类发展的历史上,马尔可夫链是第一个从理论上被提出并加以研究的随机过程模型,它包含了丰富的数学理论,与其他数学分支相互影响与渗透.很多数学问题都可以通过建立马尔可夫过程概率模型,然后运用概率论及随机过程的理论与方法进行研究.另外,随着研究的深入和时代的发展,马尔可夫链在经济学、生物学、物理学、化学、军事学、天文学等跨学科领域都引起了连锁反应,衍生出一系列新课题、新理论和新学科.当前马尔可夫链的理论研究,方兴未艾.
从中学数学教学的角度看,一方面,概率统计与学生实际生活的联系最为直接和紧密,该板块强调理论联系实际,重视基本概念与数学建模的有机结合,要求学生在掌握相关概念和公式的基础上,建立初步的概率模型的意识以及解决实际问题的能力.因此,概率统计知识是数学模型的重要载体.近年来,高考概率统计试题对于数学模型的考查变得更加精细与完善.因此,研究吸收态等典型的数学模型是非常有意义的.另一方面,马尔可夫链模型也是高中阶段开展数学项目化学习的良好素材.一些与生活息息相关的问题,如预测股票涨跌、天气变化、银行贷款等,都可以结合马尔可夫链模型来解决.这些问题兼顾趣味性与挑战性,充满了生活气息,对学生有十足的吸引力,同时里面涉及许多的知识点,如矩阵乘法、递推数列、线性方程组等,更是开阔学生视野、提升数学素养的极佳附着点与生长点.

