中学数学探究性作业设计的基本策略

吴光潮

(广州市黄埔区教育研究院,广东 广州 510799)

《义务教育数学课程标准(2022年版)》(以下简称《课标》)指出,初中学业水平考试(以下简称“中考”)命题原则要坚持素养立意,凸显育人导向,以核心素养为导向的考试命题,要关注数学的本质,关注通性通法,综合考查“四基”“四能”与核心素养.适当提高应用性、探究性和综合性试题的比例,题目设置要注重创设真实情境,提出有意义的问题,实现对核心素养导向的义务教育数学课程学业质量的全面考查[1].在落实“双减”、提质增效的当下,“做好初中数学探究性作业设计,落实作业改革”是推进课程改革的重要一环.本文系统梳理了中学数学探究性作业设计的基本策略,以助力教师开展数学探究性作业的设计及实施,实现“教考一致”,落实学科育人的课改精神.

1 探究性作业的基本内涵

“探究性作业”普遍认同的定义源自“探究性学习”.人民教育出版社科研部的任长松认为,探究性学习是指学生围绕一定的问题、文本或材料,在教师的帮助和支持下,自主寻求或建构答案、意义、理解与信息的学习活动或过程.这与《课标》倡导“实施促进学生发展的教学活动”的理念高度契合:引导学生在真实的情境中发现问题和提出问题,利用观察、猜测、实验、计算、推理、验证、数据分析、直观想象等方法分析问题和解决问题.基于此,笔者将其进行如下界定:探究性作业指在探究性问题驱动下,以培养数学关键能力、核心素养为导向,学生基于自身知识基础与思维方式展开自主探究,呈现整个发现、提出、分析、解决问题的探究过程的数学作业.探究性作业有助于学生在“做”“思考”“实验”“探究”等一系列的活动中发现和解决问题,体现思维的问题性、深刻性、灵活性、批判性和独创性;有助于学生在呈现个性化思考的过程中获得高阶思维(分析、综合、评价、创造),培养和发展学生的逻辑推理、数学抽象、直观想象、数学建模、数学运算、数据分析等核心素养,从而发展实践能力和创新能力.

数学探究性作业有实践性、学生主体性、过程性、知能并重性等主要特点.相比传统作业,探究性作业更强调“做中学”,突出实践的作用,体现了作业的实践性,有利于提升学生学以致用的能力;探究性作业更强调“选择性”和“开放性”,学生自主选择工具、知识和完成方式等,突出学生个体差异化发展,体现了作业的学生主体性,有利于因材施教,落实课改精神;探究性作业更强调“自主构建的完成过程”,作业的完成过程和评价过程是作业设计的重要环节,突出学生知识与能力形成的过程,体现了作业的详细、客观、公平的过程性;探究性作业更强调“四基”“四能”,在完成探究性作业的过程中,学生基于“四基”逐渐养成观察、猜想、验证、分析、推理、解决问题的逻辑思维习惯,从而培养和发展“四能”,提升综合运用知识的能力,体现了作业的知能并重性,有利于发展学生的数学核心素养.

2 探究性作业的基本类型

数学探究性作业按不同的分类标准会有不同的类别.本文从内容角度将其简单分为知识探究型作业和学术研究型作业两大基本类型.

2.1 知识探究型作业

知识探究型作业从完成方式上又细分为阅读型、猜想型、综合型、实验型、实践型.实际上,知识探究型作业可以从完成方式的角度同时融合多种类型.

2.1.1 阅读型作业

数学阅读型作业提供了一份数学文字材料或图表信息,让学生在阅读中探索、发现,获取信息,运用规律,相互交流,考查学生的概括、归纳﹑整合能力.

例1问题情境:小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉,为了确定售价,小莹帮妈妈调查了附近A,B,C,D,E这5家花卉店近期该种盆栽花卉的售价与日销售量情况,记录如表1所示:

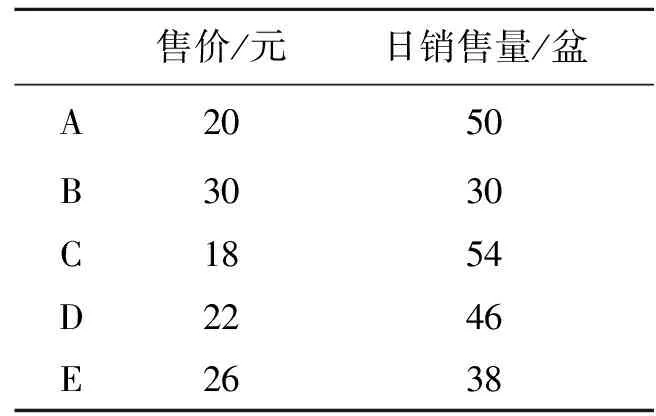
表1 盆栽花卉售价与日销售量情况

1)数据整理:请将表1中的调查数据按照一定顺序重新整理,填写在表2中.

表2 重新整理后的售价与日销售量情况

2)模型建立:分析数据的变化规律,找出日销售量与售价间的关系.

3)拓广应用:根据以上信息,小莹妈妈在销售该种花卉时,①要想每天获得400元的利润,应如何定价?②售价定为多少时,每天能够获得最大利润?

(2023年山东省临沂市数学中考试题第23题)

评注题目引导学生经历“生活情境(指定情境)→获取数据(直接给出)→数据整理→模型建立→拓广应用”的过程,渗透数学建模思想.其中“按照一定顺序重新整理”“分析数据的变化规律”等信息的提取和理解是关键,促使学生联系“描点法”作函数图象的基本活动经验,通过列表、作图、观察,利用几何直观观察“点列”,判断并建立一次函数模型从而解决问题.

2.1.2 猜想型作业

数学猜想型作业能充分激发学生的观察力、想象力、推理类比能力等,在初中数学实施猜想型作业比完整的探究作业更精短、灵活,可以为综合的探究性作业铺路奠基.

例21)观察分析:在一次数学综合实践活动中,教师向学生展示了如图1～3所示的3幅图形,请你结合自己所学的知识,观察图中阴影部分构成的图案,写出3个图案都具有的2个共同特征:______,______;

图1

图3

2)动手操作:请在图4中设计一个新的图案,使其满足你在1)中发现的共同特征.

(2023年山东省枣庄市数学中考试题第18题)

评注题目呈现了3个具有“轴对称”“中心对称”“面积相等”特征的图形,引导学生观察、归纳、猜想.

2.1.3 综合型作业

数学综合型作业是指综合运用横向或纵向多维度的知识、方法,以培养和发展学生“四基”“四能”为主要目的、纯数学情境的题目.

例3如图5,二次函数y=-x2+4x的图象与x轴的正半轴交于点A,经过点A的直线与该函数图象交于点B(1,3),与y轴交于点C.

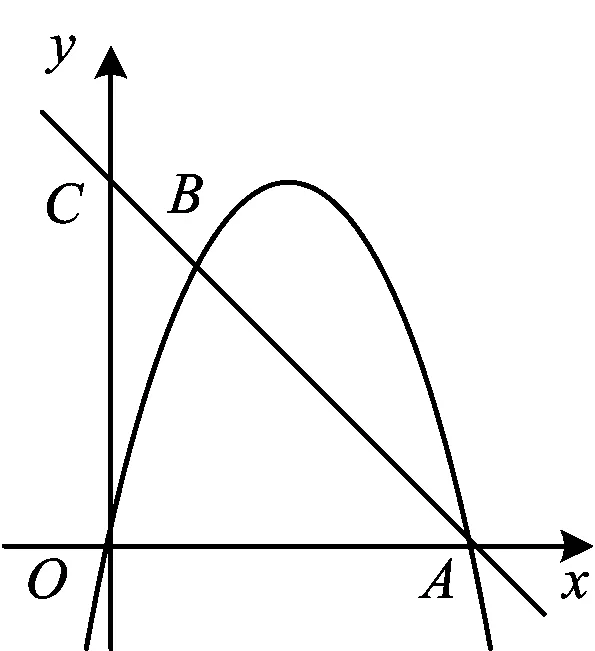
图5

1)求直线AB的函数表达式及点C的坐标.

2)如图6和图7,点P是第一象限内二次函数图象上的一个动点,过点P作直线PE⊥x轴于点E,与直线AB交于点D,设点P的横坐标为m.

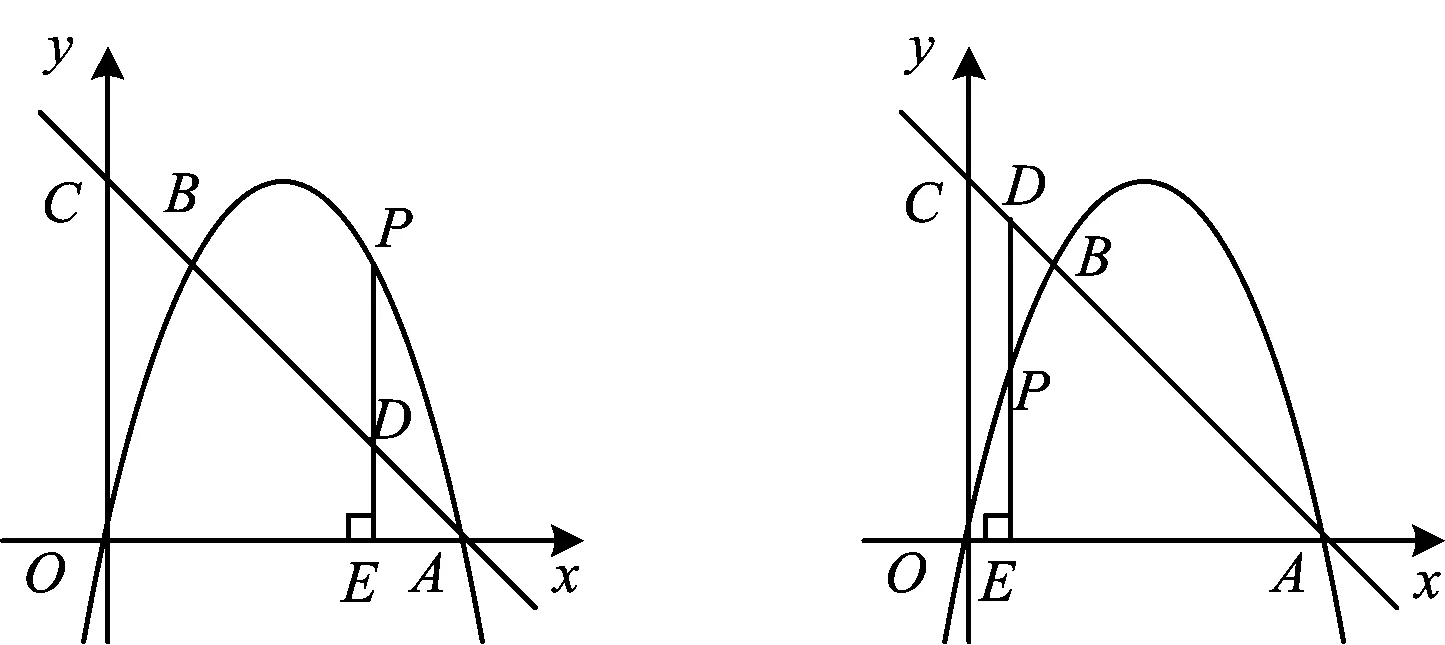
图6

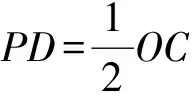
②如图8,当点P在直线AB上方时,联结OP,过点B作BQ⊥x轴于点Q,BQ与OP交于点F,联结DF,设四边形FQED的面积为S,求S关于m的函数表达式,并求出S的最大值.

图8

(2023年山西省数学中考试题第23题)

评注此题属于二次函数综合题,将二次函数的性质、一次函数的性质、特殊四边形的判定和性质等知识综合考查,运用分类讨论思想是解题关键,属于中考压轴题.综合型探究性作业多指此类具有综合性,有一定挑战性和思维含量的纯数学情境问题.

2.1.4 实验型作业

数学实验型作业是指以动手实验为情境特征和探究基础的作业.实验探究型作业凸显“做中学”,使学生通过实验去发现、提出问题,从而在分析、探究、解决问题的过程中,巩固数学知识、形成关键能力、发展核心素养.

例4如图9,将矩形纸片ABCD对折,使AD与BC重合,展平纸片,得到折痕EF;折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AM,点B,E的对应点分别为点B′,E′,展平纸片,联结AB′,BB′,BE′.请完成:

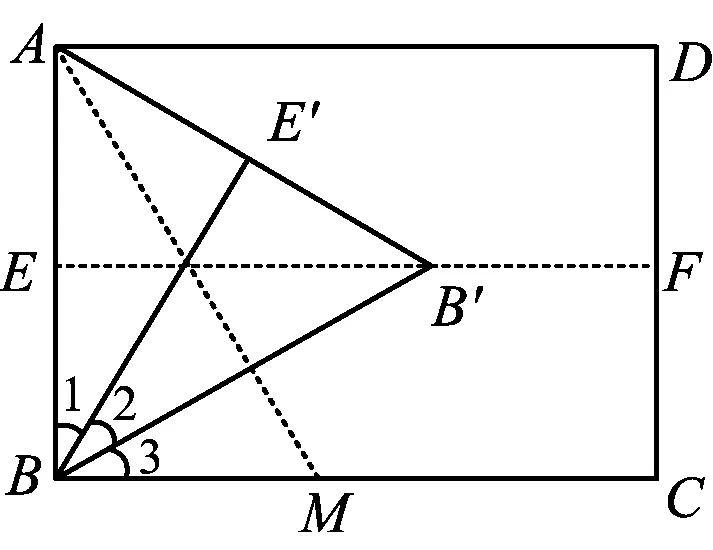
图9

1)观察图9中的∠1,∠2和∠3,试猜想这3个角的大小关系;

2)证明1)中的猜想.

3)类比操作:如图10,N为矩形纸片ABCD的边AD上的一点,联结BN,在AB上取一点P;折叠纸片,使点B,P重合,展平纸片,得到折痕;折叠纸片,使点B,P分别落在EF,BN上,得到折痕l,点B,P的对应点分别为点B′,P′,展平纸片,联结P′B′,BB′.请证明BB′是∠NBC的一条三等分线.

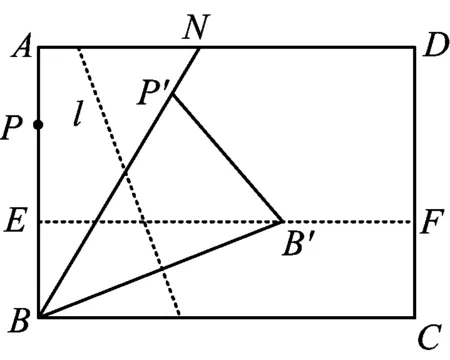
图10

(2023年广西壮族自治区数学中考试题第26题节选)

评注此题以折纸这个操作简单、富有数学趣味的动手实验活动为情境载体,开展数学探究,探索数学奥秘.大量解决问题的点、线、角的关系等关键条件都隐含在折纸过程中,综合考查学生问题解决的必备知识,以及几何直观和空间想象等核心素养,对学生发现问题、提出问题能力的培养具有重要作用.

2.1.5 实践型作业

数学实践型作业将自主探究、实践体验、合作交流的学习方式与更广泛的社会实践有机结合,形成体现丰富多彩的学习环境的相关作业,如调查型作业、体验型作业等.

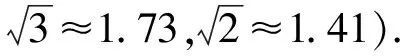
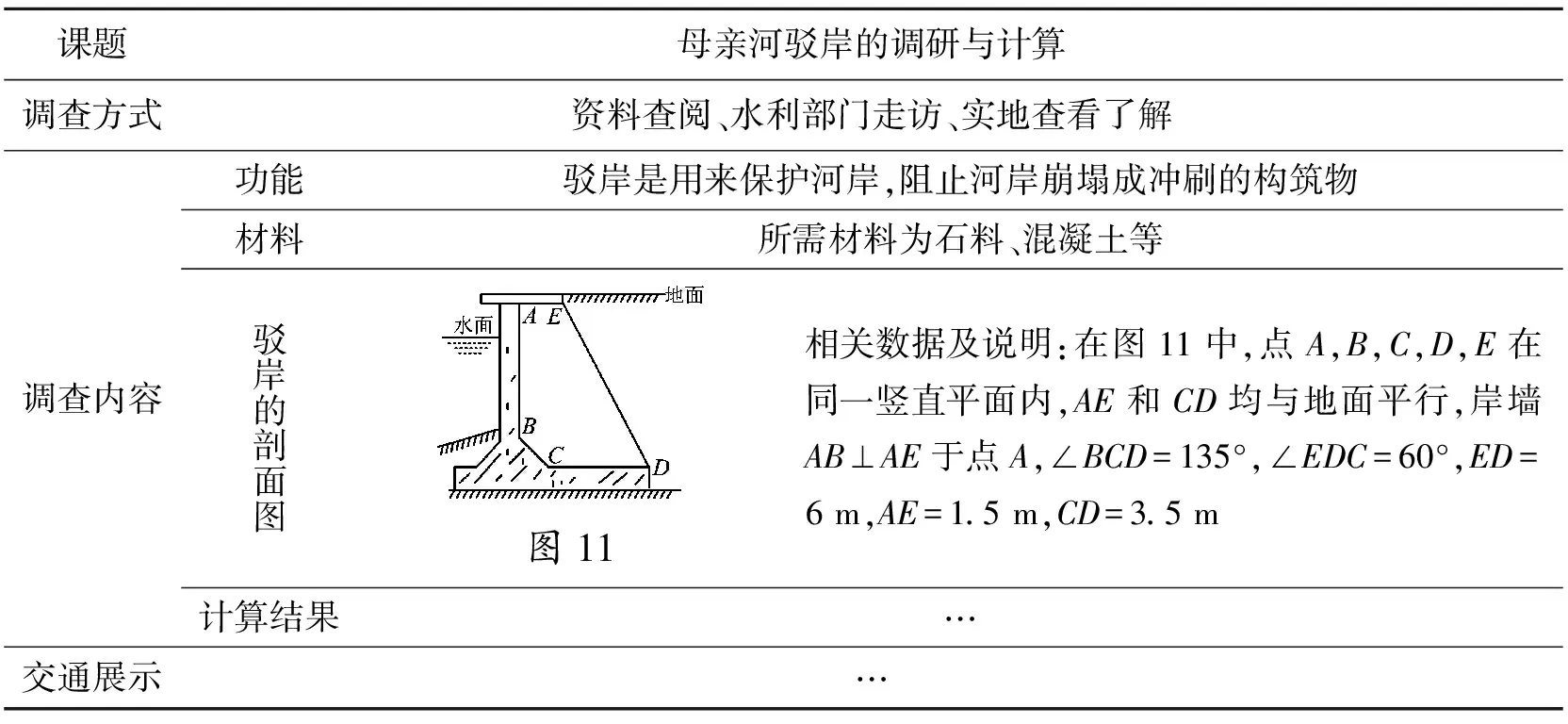
表3 活动报告

(2023年山西省数学中考试题第20题)

评注此题以“综合与实践”主题中实践调查课题活动为背景,创设真实情境,并以活动报告的形式呈现解决问题的主要信息,同时渗透了学术调查的部分元素,体现了项目化学习的理念和学科育人的课程思政功能.

2.2 学术研究型作业

学生在学习过程中对某个数学内容或相关问题产生浓厚兴趣,教师可从中选择代表性的主题作为短程、中程或长程项目化作业,引导学生去探索研究,写出研究报告等成果.例如,“综合与实践”类主题,可以调查当地水资源的利用和污染状况并提出建议.

3 探究性作业的设计原则

在素养导向、以生为本的当下,作业设计理念既要关注知识、能力的考查,也要关注素养立意,彰显育人本质.基于此,数学探究性作业需要遵循以下3个基本原则.

1)设计分层,注重面向全体学生.

数学探究性作业的完成过程要注重面向全体学生,有层次性,体现对个性差异的关注.由于探究性作业相比常规作业,多具有开放性、综合性、探究性、难度较大等特点,尤其对学习基础不扎实的学生“不太友好”.但探究性作业作为学科育人的一种方式,必须坚持以“学生的发展”为核心,面向全体,尊重个体差异,让优等生、学困生都有收获.层次性指作业探究过程有层次,完成方式和路径多样,如问题解决能逐层进阶、一题多解、举一反三、一题多变等.

2)情境科学性,凸显问题探究价值.

数学探究性作业的问题情境要科学设置,能真实探究,促进学生的学习方式从“被学”向“自学”转变.情境科学是指问题嵌套在真实的情境中,问题是学生未知的,能激发学生的好奇心与探究欲;解决问题的工具和条件隐含在情境中,需要学生进行批判性选择和转化;问题解决的方法不唯一,甚至最终答案也不唯一.问题情境要能引导学生从多个角度对有关问题做出思考和价值判断,并能进行自主探究,从而使得情境对培养学生的参与意识、决策能力、创新意识以及科学精神、人文精神具有积极意义.探究性作业是探究式教学的延伸,可以促进教师教学方式、学生学习方式的进一步转变,并形成良性循环,最终有效提升学生的探究意识和探究能力.

3)注重开放性,强化作业育人功能.

数学探究性作业要注重作业的开放性,以强化高阶认知能力的培养.探究性作业的探究性与开放性紧密联系.开放性作业设计可以是任务本身具有开放性,学生通过经历发现问题、提出问题、分析问题、解决问题的过程,多角度、全方位地分析探索;可以是问题解决方法或任务完成过程具有开放性,切入口较宽,不能靠机械记忆、套用模式来寻求解决问题的方案,而需要运用多种思维方式;可以是答案不唯一,解法灵活多样;也可以是多种开放的结合.开放性的作业更能有效激发学生的探究意识,以及独立思考与合作探究的能力,有利于认知目标分类学体系中理解、应用、分析、综合、评价、创造等高阶认知能力的培养.

4 探究性作业的设计策略及案例分析

4.1 设计数学探究性作业的基本策略

基于中学数学探究性作业的内涵、特点、类型及设计原则,可结合设计框架(如图12)设计探究性作业[2].

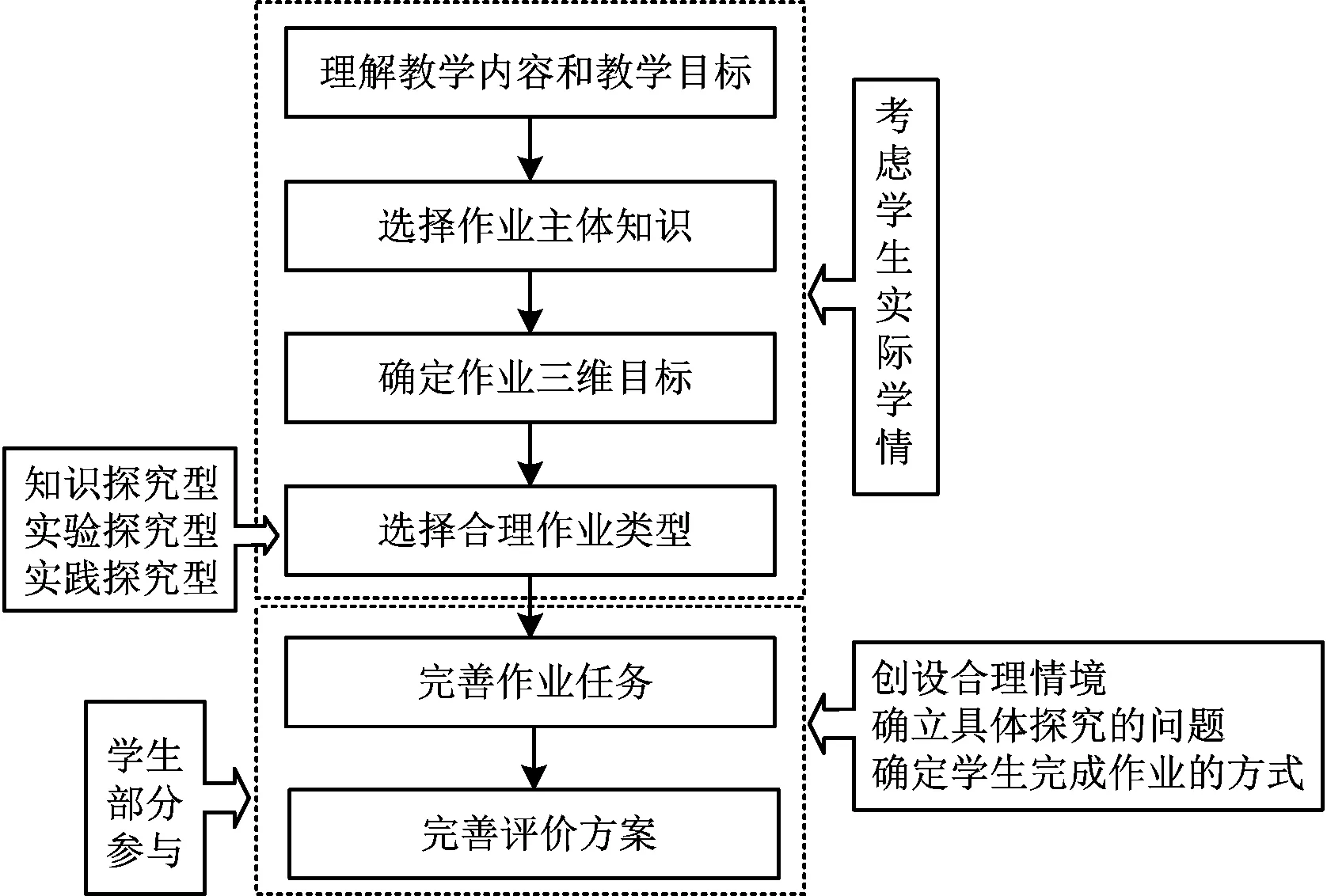
图12 探究性数学作业的设计框架

首先,明确设计方向与类型.即在深刻理解《课标》、透彻分析教材、准确把握学情、明确素养导向的教学目标的基础上,确定探究性作业的方向、类型,明确作业设计所蕴含的核心素养.

其次,设置作业情境与任务.通过整合优化教材中原有的探究性作业、改编教材或中考试题中的作业素材、联系社会生产生活实际等方式进行作业情境与任务设计,着力设计能激发求知欲的情境与任务,以激活、强化学生在情境与任务中运用特定必备知识、关键能力、核心素养和具体目标行为解决问题的能力;将作业蕴含的核心素养表现特征具体化,并融入作业的探究过程设计中,促使学生在作业探究过程中有充分的展现空间.

最后,强化内容审查与改进.对情境的趣味性、综合性与实践性进行优化,包括情境对学生主动性学习、综合性学习、问题解决能力培养等方面的促进效果;解决作业情境创设中的常见问题,如情境创设缺乏真实性、情境创设“穿靴戴帽”(情境任务与作业目标联系不紧密,只是物理意义上的拼装)、情境创设中的伦理问题等,确保情境真实(现实存在能重复或模拟的,反映真实生活对学生学习的要求)、复杂(需要进行判断、分析、探索、整合与创新,以展现必备知识、关键能力,反映现实生活的复杂性)、有效(能有效激发学生的目标行为,促进深度学习发生,使学习表现得到准确评价);对探究过程、完成形式等载体进一步打磨,也可结合评价量表、量规等工具对评价方案进行完善.

4.2 数学探究性作业的案例赏析

图13

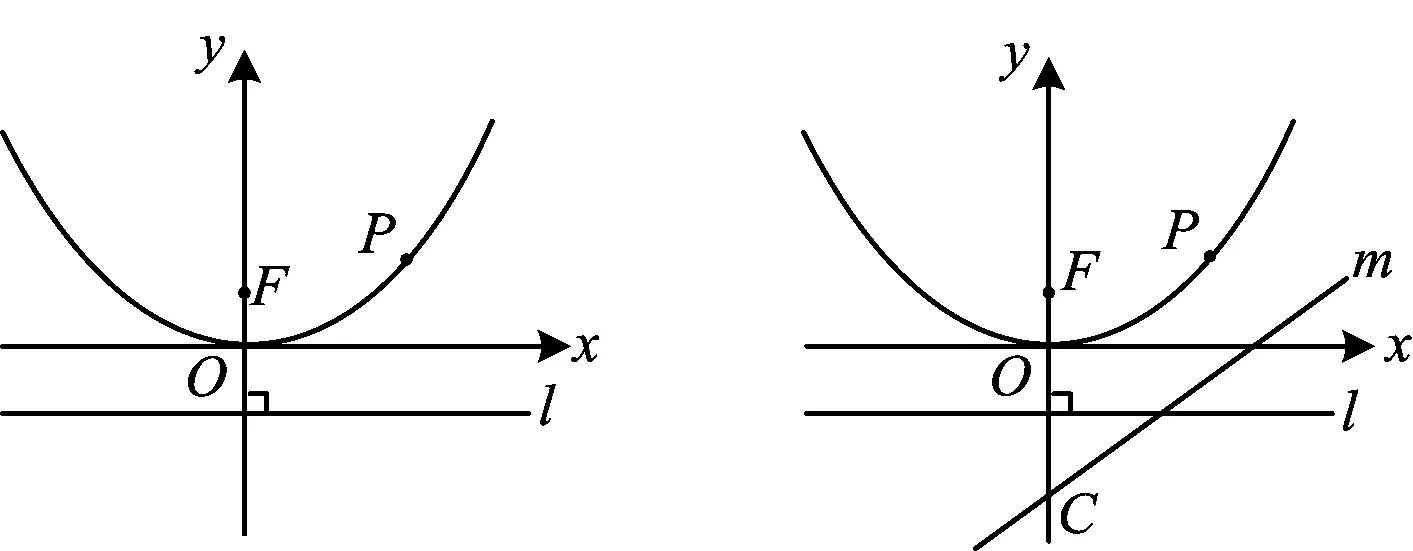
图14

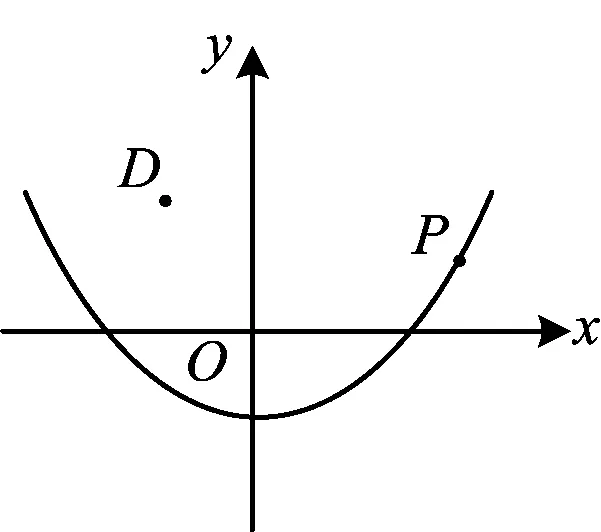
图16

(2023年湖北省鄂州市数学中考试题第23题)

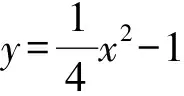
数学探究性作业能促进教与学方式的转变,加强“教考一致”,落实学科育人.数学教学要以学生发展为中心,数学教师要积极开展数学探究性作业的设计与实践,在作业设计中增加探究性作业的实践性、综合性、探究性、开放性,从而更好地发挥作业的育人功能,促进学校教育教学质量的提升.