化静为动,巧用“等腰翻折体”突破立体几何题
潘一力, 顾予恒
(杭州第二中学钱江学校,浙江 杭州 311215)
引入空间向量后的立体几何问题,走上了代数化的道路,这对许多空间想象能力较弱的学生来说无疑是个福音.对于题目中给出的常规几何结构,如三线垂直、线面垂直、面面垂直,学生都能驾轻就熟地建立起空间直角坐标系.许多以往觉得困难的立体几何问题,只要通过程序化的运算就能解决.
立体几何研究的对象是各种几何体,其中一些因具有某些特征而被称为模型,如全等体、鳖臑体、阳马体、墙角体等[1].有一个几何体模型备受命题者青睐,那就是“等腰翻折体”模型.综观2023年全国数学高考试题,新课标Ⅱ卷第20题和乙卷理科第19题都考查了这个模型.笔者通过梳理近几年高考试题以及各省市模考题,探究如何根据题干给出的条件,挖掘“等腰翻折体”,从而快速且模式化地解决问题.
1 初识“等腰翻折体”模型
一般的几何体既可以看成是静态的切割体(即从长方体中切割得到的),也可以看成是动态的翻折体(由平面图形翻折得到的)[2].


图1
1)证明:PO⊥平面ABC;
2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.
(2018年全国数学高考Ⅱ卷第20题)
分析仔细解读此题的条件,发现这个三棱锥里隐藏了4个等腰三角形,其中△ABC和△APC这两个等腰三角形有一条公共的底边AC.这个三棱锥可以看成是由两个同底的等腰三角形沿着底边翻折而成,它既具有翻折的动态特点,又具有等腰的几何特征.
一般地,将两个等腰三角形组成的四边形沿三角形的公共底边翻折形成的三棱锥,我们称之为“等腰翻折体”.如图2,三棱锥P-ABC就是由四边形PBAC沿边BC翻折而成,可以记为P-BC-A.

图2
2 初探“等腰翻折体”模型的性质
性质1PB=PC,AB=AC.
性质2取BC的中点O,联结PO,AO,则BC⊥平面POA.
性质3以O为坐标原点、OA为x轴、OC为y轴、过点O且垂直于底面ABC的直线为z轴建立空间直角坐标系,则点P在平面xOz内.
性质4若PO=a,则点P落在以O为圆心、a为半径的圆上,其位置由二面角P-BC-A决定.记∠POA=θ,点P坐标为(acosθ,0,asinθ).
3 挖掘隐藏的“等腰翻折体”模型
类型1以角度为载体.
例2如图3,在四面体A-BCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
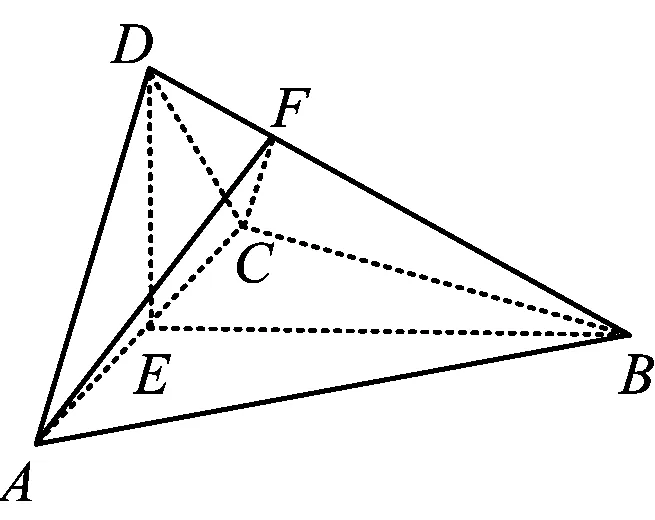
图3
1)证明:平面BED⊥平面ACD;
2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求三棱锥F-ABC的体积.
(2022年全国数学高考乙卷文科理科第18题)
分析由AD=CD,∠ADB=∠BDC,DB=DB,知△ADB≌△CDB,故BA=BC,△ABC是一个等腰三角形.又由条件知△ADC是等腰三角形,且两个三角形共用了一条边AC,于是找到了等腰翻折体D-AC-B.要注意根据题干条件,四面体A-BCD并没有唯一确定,可视为△ADC在翻折过程中的任意位置所形成的三棱锥D-ABC都符合条件.
第1)小题只是定性的研究,由性质2知AC⊥平面BED,从而平面BED⊥平面ACD.
第2)小题长度条件的加入,使得问题从定性研究转为定量求解.相当于△ADC恰好翻折到BD=2的位置,此时三棱锥D-ABC也唯一确定了.

评注此题的几何解法充分挖掘了等腰翻折体的“翻折”过程,注意到图形动态变化的特点.长度与角度等定量条件的加入,使得图形唯一确定,从而才能求体积的确定值.
同样的类型也出现在2023年浙江省杭州市高三数学二模试卷中,这里用空间向量的方法来解决.
例3如图4,在三棱锥S-ABC中,底面△ABC为等腰直角三角形,∠SAB=∠SCB=∠ABC=90°.

图4
1)求证:AC⊥SB;

(2023年浙江省杭州市高三数学二模试题第19题)
分析易知SA=SC,从而S-AC-B是一个等腰翻折体.仅凭题干条件,三棱锥S-ABC依然是不确定的几何体.


所以
AC⊥SB.


评注此题是用坐标法解决问题,利用性质4来设点是成功的重要一步.
例4如图5,在三棱锥D-ABC中,AB=BC=CD=DA,∠ABC=90°,E,F,O分别是棱BC,DA,AC的中点,记直线EF与平面BOD所成角为θ,则θ的取值范围是

图5
( )
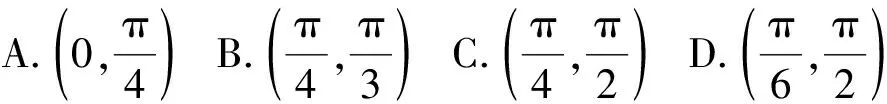
(2021年1月浙江省高中学业水平考试数学试题第18题)
分析注意到AB=BC=CD=DA,因此,这是一个等腰翻折体.以动态视角来看,这个几何体可以看成是一个正方形沿着对角线AC翻折得到,因此,题中点D的位置是不确定的.随着翻折角度的变化,θ也跟着变化.


因为cosα∈(-1,1),所以
即
故选C.
评注此题限制条件的“不足”,让几何体变得不唯一确定,于是从静态求值转变为动态求范围,经历翻折问题一般化的过程.


图6
1)证明:EF∥平面ADO;
2)证明:平面ADO⊥平面BEF;
3)求二面角D-AO-C的大小.
(2023年全国数学高考乙卷理科试题第19题)
分析由BF⊥AO易得F为AC的中点,从而OF是BC的中垂线,故BF=FC.由PB=PC,我们找到了等腰翻折体P-BC-F.


评注由于等腰翻折体建系的优势,点P的坐标只包含两个未知数,利用方程的思想,就可以求出点的坐标.有了所有点的坐标,后续证明面面垂直或求二面角就易如反掌.
类型2以多面体为载体.
例6如图7,在三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点.

图7
1)证明:BC⊥DA;

(2023年全国数学高考Ⅱ卷第20题)
分析由△ADC≌△ADB知AC=AB,可找到等腰翻折体A-BC-D.
若设DA=1,则由题目条件知等腰翻折体的每条边长都可求,不难发现这个等腰翻折体形成的二面角恰好为直二面角,可以建立如图7所示的空间直角坐标系,后面的解答过程不再赘述(略).
类型3以四棱锥为载体.

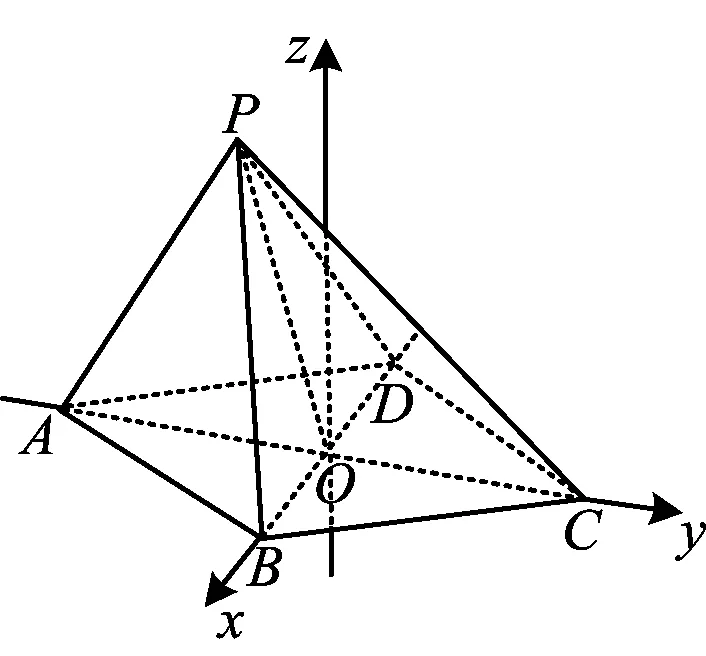
图8
1)证明:平面PAC⊥平面ABCD;
2)若PA⊥PC,求平面PAB与平面PBC夹角的余弦值.
(2023年广东省深圳市数学一模试题第19题)
分析由PD=PB和菱形ABCD易得等腰翻折体P-BD-A.由BD⊥平面PAC,得平面PAC⊥平面ABCD.

类型4以斜棱柱为载体.


图9
1)证明:A1A=A1C;

(2023年广东省深圳市数学二模试题第19题)
分析例8从结论倒推,由于第1)小题要证A1A=A1C,结合题干条件AB=BC易知这个斜棱柱里藏着一个等腰翻折体A1-AC-B.
第1)小题简证:不妨取AC的中点O,联结A1O和OB.由等腰翻折体性质2知AC⊥平面A1OB,因此,可以反过来通过证明AC⊥平面A1OB来说明A1A=A1C.显然由于AC⊥OB,AC⊥A1B,可得AC⊥平面A1OB.

类型5以棱台为载体.
例9如图10,在正三棱台ABC-DEF中,M,N分别为棱AB,BC的中点,AB=2DE.

图10
1)证明:四边形MNFD为矩形;
2)若四边形MNFD为正方形,求直线BC与平面ACFD所成角的正弦值.
(2023年山东省济南市数学二模试题第19题)
分析许多学生卡在了第1)小题,不知道如何证明MN⊥MD.事实上,如果能够在这个正棱台中发现等腰翻折体,问题就迎刃而解了.
将正三棱台ABC-DEF补成正三棱锥,如图10所示.由于PA=PC,AB=BC,易得等腰翻折体P-AC-B,取AC的中点O,由等腰翻折体性质2知AC⊥平面POB,故AC⊥PB.由于MD∥PB,MN∥AC,因此MN⊥MD.
对于第2)小题,若MNFD为正方形,则正三棱锥P-ABC就变成正四面体,线面角呼之欲出.
例10如图11,在三棱台ABC-A1B1C1中,A1C1=4,AC=6,D为线段AC上靠近C的三等分点.
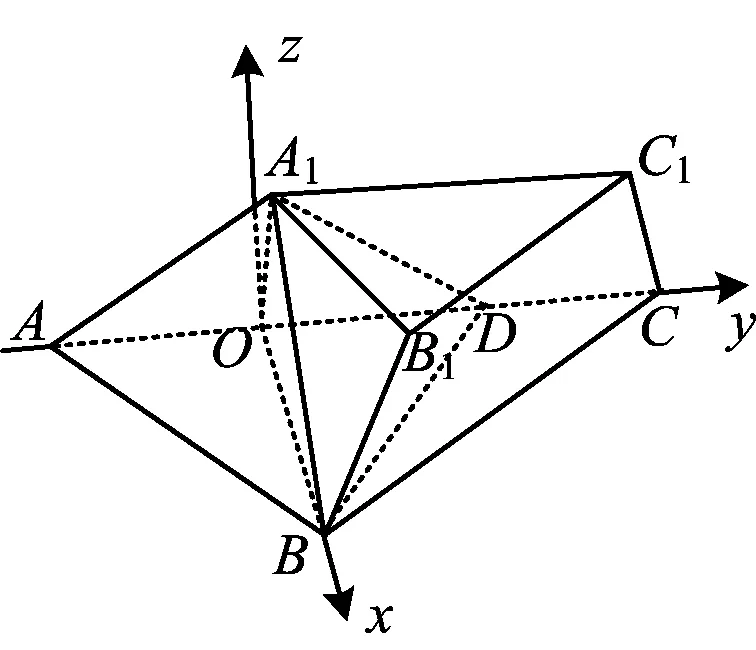
图11


(Z20名校联盟2023届高三第三次数学联考试题第20题)


4 利用“等腰翻折体”解决立体几何问题的基本步骤
第1步,理清题干条件,找到“等腰翻折体”.
值得关注的题干条件包括线段长度相同、角度相同、等边三角形、等腰三角形、直角三角形斜中线、菱形等.若遇台体,则可尝试补全为锥体再找是否存在等腰三角形,也可关注台体底面图形的边长和夹角,在内部找等腰三角形.
第2步,以“等腰翻折体”公共底边的中点为原点建立空间直角坐标系.
这样建系的好处是等腰翻折体的顶点在坐标平面内,点的坐标越简单,后续向量的坐标运算越简便.
第3步,求出“等腰翻折体”顶点的坐标(几何法、代数法),代数求解问题.
几何法需要找到等腰翻折体的二面角大小,通常情况下是由这两个等腰三角形顶点在翻折后连成的线段长度决定的.代数法本质上就是方程思想.由于等腰翻折体的建系方式使得一个顶点落在坐标平面内,因此,点的坐标只含两个未知数,利用两个条件转化为两个方程求解即可.
5 结束语
等腰翻折体在近几年的高考试题和模拟题中出现的频次很高,是一个值得引起教师和学生重视的基本模型.它变化多端,不仅存在于三棱锥,也深藏于四棱锥、斜棱柱和棱台之中.两个同底的等腰三角形的结构不仅会以长度相等的形式给出,也可以以角度相等的形式出现.
“化静为动”是利用等腰翻折体解决立体几何问题的核心.在静态的图形中找到动态的等腰翻折体,从而成功地建立空间直角坐标系,为定性证明和定量求值做好铺垫.熟悉基础模型,可以帮助学生突破建系和设点的难度.
《普通高中数学课程标准(2017年版2020年修订)》中指出,在空间向量与立体几何的教学中,要鼓励学生灵活运用向量法与综合几何法,从不同角度解决立体几何问题,通过对比体会向量法的优势.而本文阐述的利用等腰翻折体模型的解题方法充分体现了向量法的优势.对于学生而言,理解起来并不困难,是一个易于掌握的“模式化”解题方法.

