核心素养导向下的单元章末复习教学与思考——以人教A版“空间直线、平面的垂直”复习课为例

蒋亚军, 任伟芳

(1.宁波市第四中学,浙江 宁波 315016;2.宁波市教育局教研室,浙江 宁波 315100)

2023年6月,宁波市教育局教研室组织了以“新课标新教学下的高中数学章末单元复习课研讨”为主题的课堂教学比赛活动,课题为“空间直线、平面的垂直”的复习课,共有17位选手以同课异构的形式进行角逐.笔者依据单元整体教学的理念,结合授课内容特点和学生认知水平,构建了一节以鳖臑模型中寻找垂直的历程为线索、展现数学思想方法和研究思路的课堂.笔者执教的“借助鳖臑模型整合空间垂直——以‘空间直线、平面的垂直’复习课为例”得到了评委老师和学生的一致好评,荣获一等奖.现将笔者参赛的教学设计和课后反思整理成文,与同行分享,不当之处敬请批评指正.

1 教材分析

“空间直线、平面的垂直”是人教A版《普通高中教科书·数学》(以下统称“高中《数学》”)(必修第二册)第八章“立体几何初步”中最后一个单元的内容.因此,这节复习课不仅能够综合提升线线垂直、线面垂直及面面垂直学习的效果,还承担了垂直这一单元小结课的功能,对进一步完善学生的立体几何知识体系起着重要的作用.类比空间直线、平面的平行关系的研究,得到空间直线、平面的垂直关系的研究思路,体会研究几何对象的基本方法,感受研究空间位置关系“直观感知→操作确认→推理论证→度量计算”的一般研究思路.

2 教学目标

从知识层面看,学生学习了线面垂直、面面垂直的判定定理和性质定理,了解了异面直线所成角、线面角和二面角的定义和求法;从方法层面看,学生能够类比空间直线、平面平行关系的研究思路和路径,对空间直线、平面垂直关系进行研究;从单元层面看,通过对几何对象的研究方法及空间位置关系的研究思路的学习体会,学生能够提升认识和探索空间图形的能力.课堂中形成了本节课的知识网络和素养落实结构图,如图1所示.

基于以上分析,确立本节复习课的教学目标为:

1)通过直观感知生活中的垂直现象,利用推理论证并应用线面垂直、面面垂直的判定定理和性质定理,理解这些定理之间的逻辑关系,利用定义会找异面直线所成角、线面角和二面角;

2)体会“直观感知→操作确认→推理论证→度量计算”的研究思路;

3)落实数学抽象、直观想象、逻辑推理、数学建模等核心素养.

3 教学重点与难点

教学重点:通过鳖臑模型回顾线面垂直、面面垂直的判定定理和性质定理.

教学难点:利用鳖臑模型发现线线角、线面角、二面角之间的数量关系.

4 教学过程

4.1 折纸游戏抽象模型

课堂引入分为两个环节:一是折纸游戏,事前准备好纸片,教师边演示边讲解,学生完成鳖臑的制作;二是用PPT投影高中《数学》(必修第二册)第158页的例8、第160页的例10和第163页的练习7,引导学生从3个熟悉的例题、习题中抽象出鳖臑模型.

师:这些都是我们熟悉的教材上的例题和习题,观察题目中的图形(如图2),它们有什么共同特征?

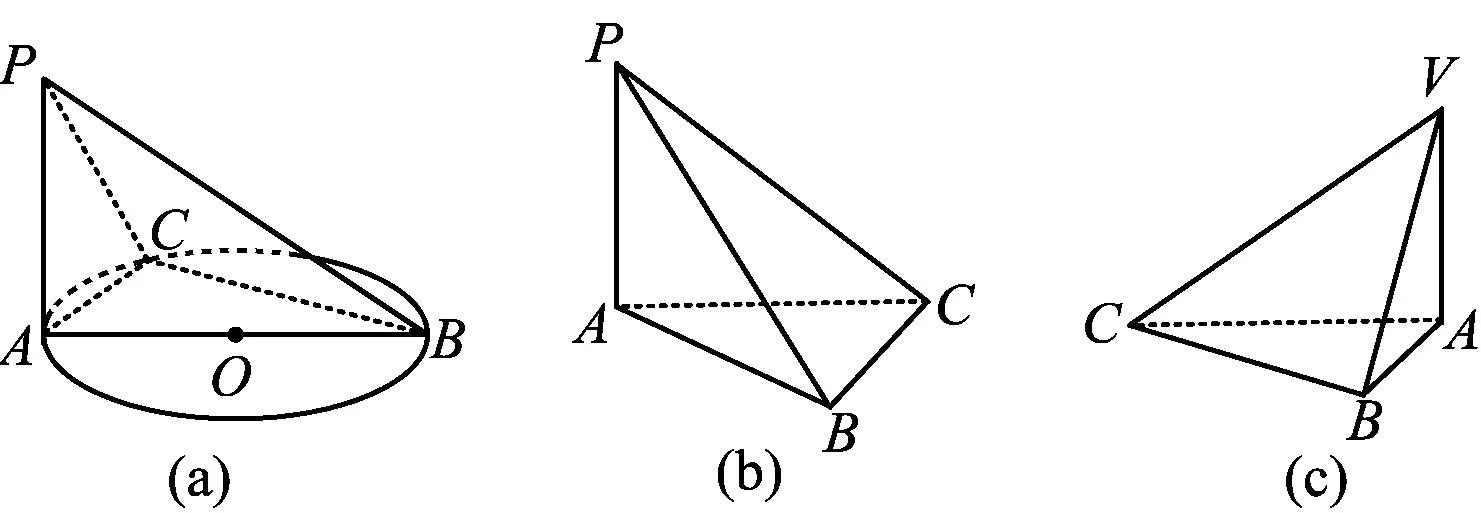
图2

生1:都是由4个直角三角形组成的三棱锥.

师:很好,这种底面是直角三角形,有一条侧棱垂直于底面,垂足不是直角顶点的三棱锥称为鳖(biē)臑(nào).

早在公元一世纪左右,我国古代的数学名著《九章算术·商功》指出:斜解立方,得两堑堵.斜解堑堵,其一为阳马,其一为鳖臑.阳马居二,鳖臑居一,不易之率也.

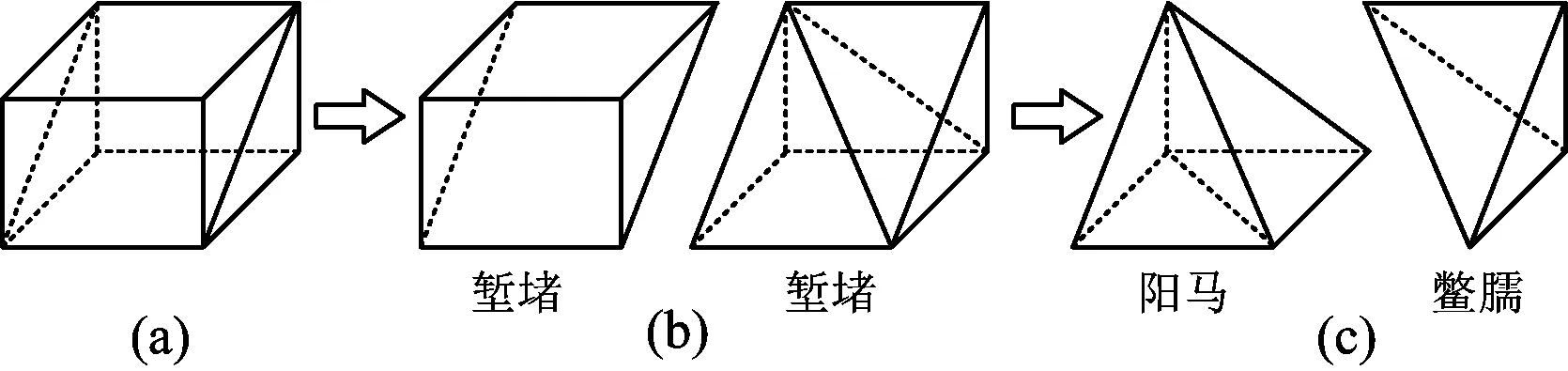
图3

鳖臑不仅可以由长方体切割得到,也可以把它补形成长方体.本节课以鳖臑为载体,回顾整理空间直线、平面的垂直关系.

设计意图从传统文化折纸游戏引入,激发学生的兴趣,学生参与度高.折出鳖臑后有两个方面的意图:一方面,使学生感受到数学是有趣的、好玩的;另一方面,抓住学生的好奇心,使学生产生“鳖臑有什么用?”的疑问,为本节课的学习提供顺其自然的需求.通过展示学生熟悉的例题和习题,引导学生观察3个图形,归纳总结共同特征,并抽象得到鳖臑模型.借助数学名著《九章算术·商功》介绍鳖臑的由来,配合动画演示,激发学生的学习兴趣和民族自豪感,能够体会“既可以通过长方体切割得到鳖臑,又可以将鳖臑补形回到长方体”.

4.2 鳖臑的判定

问题1如图4,在三棱锥A-BCD中,AB⊥BC,AB⊥DC,BC⊥DC,你能发现哪些线面垂直?哪些面面垂直?为什么?

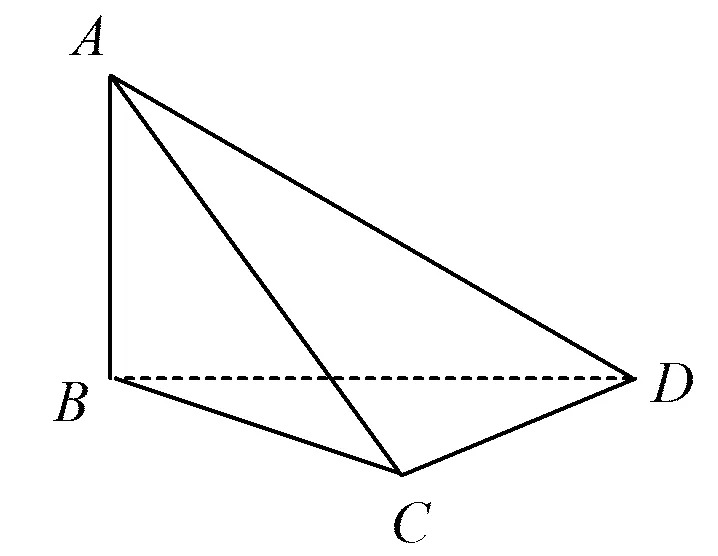
图4

追问1三棱锥A-BCD是一个鳖臑吗?

追问2如果选定AB⊥平面BCD,你能添加条件让它还是鳖臑吗?

追问3如果平面ABC⊥平面BCD,平面ABD⊥平面BCD,可以判定它是鳖臑吗?

设计意图问题1的设置可以帮助学生回顾线面垂直、面面垂直的判定定理和性质定理.学生边回答,教师边板书符号和图形语言,最后呈现线线垂直、线面垂直及面面垂直之间相互转化的框架图.为接轨新高考模式下的结构不良题型,设置开放性问题(追问2),在PPT屏幕上展示各种垂直条件让学生选择,然后再加以证明.学生在AB⊥平面BCD的前提下,容易想到添加条件“BC⊥CD”“AC⊥CD”或“平面ABC⊥平面ACD”.问题的解决体现了执果索因的思想,有利于落实学生逻辑推理的核心素养,形成知识的网络结构图.追问3可以通过直观演示直角三角板任意转动,发现不能保证BC⊥CD,故不能判定为鳖臑.

4.3 鳖臑的性质

问题2在判定三棱锥A-BCD是一个鳖臑后,你能得到哪些关于垂直方面的结论呢?

学生小组讨论后,得到以下结论:

异面直线垂直(1组):AB⊥CD;

线面垂直(2组):AB⊥平面BCD,DC⊥平面ABC;

面面垂直(3组):平面ABC⊥平面BCD,平面ABD⊥平面BCD,平面ACD⊥平面ABC;

相交垂直(4组):AB⊥BC,AB⊥BD,DC⊥BC,DC⊥AC.

4.4 鳖臑的应用

图5

(2008年浙江省数学高考理科试题第14题)

问题4如图6,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

1)求证:PA⊥BD;

2)求证:平面BDE⊥平面PAC;

3)当PA∥DE时,求三棱锥E-BCD的体积.

(2017年北京市数学高考文科试题第18题)

设计意图选择以鳖臑为模型的高考真题,使学生有熟悉感.问题3主要体现补形的思想,降低思维难度,使学生能快速完成解答.在问题4中若能找到鳖臑模型,则利用鳖臑的性质可以快速解决选择题、填空题,但解答题还是需要严格证明.其中第3)小题的解决可以直接应用体积公式,也可以通过比例关系将鳖臑补成长方体.

4.5 鳖臑再探究

问题5鳖臑模型不仅包含垂直关系,还包含数量关系——空间角和距离.如图7,请你找出直线AD与平面BCD所成的角,以及二面角A-CD-B的平面角.

图7

追问4当二面角A-CD-B为45°时,直线AD与平面BCD所成角的取值范围是多少?

追问5当直线AD与平面BCD所成角为45°时,二面角A-CD-B的取值范围是多少?

追问6设∠ADB=θ(线面角),∠ADC=θ1(线线角),∠BDC=θ2(射影角),∠ACB=φ(二面角).这些角的三角函数有什么关系呢?

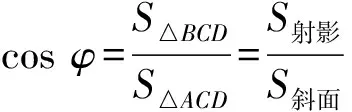
4.6 小结提升

师:请结合本节课的学习,回答下面的问题:1)本节课复习了哪些知识?2)按照怎样的路径对鳖臑进行研究?3)学习过程包含哪些数学思想方法以及核心素养?

学生总结出以下结论:

1)知识内容:借助鳖臑模型回顾了直线、平面的3种垂直关系的相互转化;

2)研究路径:定义→判定→性质→应用;

3)思想方法:模型思想、转化思想、建模思想、执果索因;

4)核心素养:数学抽象、直观想象、逻辑推理、数学运算.

师:最后用一首打油诗小结.鳖臑模型在手,三种垂直都有;线面垂直沟通,推理验证直观.

5 教学反思

1)单元复习课要制定以素养为导向的教学目标.

鳖臑不仅包含了立体几何中点、线、面的各种位置关系,有着丰富的垂直关系作为定性判断的依据,是讨论空间直线、平面的垂直关系及其相互转化的非常好的载体;还包含了立体几何千变万化的空间角,为破解定量计算以及揭示几何体基本结构与本质规律带来可能.在鳖臑的判定环节,出现了线面垂直、面面垂直的判定定理和性质定理,形成垂直关系相互转化的结构图,把零碎的知识串联起来.这样处理的效果要比直接给出定理再进行应用要好,更有利于学生理解和掌握,也关注到了文字语言、符号语言和图形语言的相互转化.在鳖臑的应用和再探究环节,精选问题,渗透切割与补形的数学思想,通过一题多解,学生能熟练地应用鳖臑模型来解决数学问题.在问题设置上接轨新高考出现的新题型——结构不良试题,具有开放性,有利于学生思维的发散,形成从直观感知到严格证明的科学研究思路.

2)单元复习课要整体关联知识方法和核心素养.

复习课的定位应该是“基础知识的掌握、基本技能的提高、基本思想方法的落实、基本活动经验的积累”[1].单元内容一般由基础知识、思想方法和核心素养加以串联.单元结构化教学要注重知识结构的“明线”和思想方法与核心素养的“暗线”[2].本节课的“明线”是围绕鳖臑展开的,从抽象出鳖臑模型开始,沿着定义、判定、性质、应用一步步展开,这也是研究几何对象的基本方法.类比平行关系的学习,沿用从简单到复杂的思路,既要掌握线面垂直、面面垂直的判定定理和性质定理,又要通过定义异面直线所成角、线面角和二面角来刻画空间图形的关系.为后续的定量计算以及空间向量的学习做铺垫,体会研究几何对象的基本方法,感受研究空间位置关系“直观感知→操作确认→推理论证→度量计算”的一般研究思路.本节课的“暗线”从数学思想和核心素养两个方面展开.从教材中的例题和习题抽象出鳖臑模型,体现了模型思想,鳖臑的判定的证明过程中有执果索因思想的体现,开放性问题的设置以及切割与补形的统一突出了转化与化归的思想,落实了数学抽象、直观想象、逻辑推理和数学运算等核心素养.

3)单元复习课要引导学生感悟数学文化的价值.

《普通高中数学课程标准(2017年版2020年修订)》指出,数学课程内容要培育数学核心素养,继承与弘扬中华优秀传统文化,坚定文化自信;要注重数学文化的渗透,不断引导学生感悟数学的科学价值、应用价值、文化价值和审美价值.中华优秀传统数学文化走进高中数学课堂强调古为今用,提升学生数学学习的文化内涵,促进核心素养的综合发展.本节课创设适合的教学问题情境,引入“鳖臑”模型,启发学生思考,引导学生把握数学内容的本质,体会古代数学家对人类的贡献.本节课围绕鳖臑模型,把本单元的知识有效地整合在一起,既有定性的判断,又有定量的计算.采用传统文化——折纸游戏引入,吸引了学生的注意,借助学生已有的知识储备,促进学生积极主动地参与本节课的学习,突出学生的主体地位,关注学生基本活动经验的积累.对我国古代数学名著《九章算术·商功》的介绍,一方面,体现了古代数学家的成就,有利于增强学生的民族自豪感;另一方面,体现了数学源于生活,又服务于生活,要做一个生活的有心人,用数学的眼光观察现实世界.这样的设计,既丰富了课堂的数学文化,又激发了学生的学习兴趣.

总之,单元整体教学视角下的章末复习课的研究与实施,需要在教学实践中不断探索和创新.学生的学习是一种特殊形式的探究,是在教师的指导下有目的、有计划、系统性地进行知识建构,学生在较短的时间内学习数学知识的过程[3].教师要遵循知识的整体性、情境的贯穿性、思维的连续性、逻辑的连贯性和方法的系统性,通过设置符合学情的问题,引导学生体悟数学对象的研究思路和研究方法,促进学生在学习活动中提高必备品质和关键能力,逐步形成正确的价值观,从而实现由“学会”到“会学”再到“乐学”的转变.