α-螺旋蛋白中三分量高阶非线性薛定谔方程的怪波解

王梦雅,陈婷婷,王立洪

（宁波大学 数学与统计学院,浙江 宁波 315211）

1973 年,乌克兰生物学家Davydov[1-2]提出生物能量和生物信息传递的孤子理论,用数学模型研究α-螺旋蛋白分子中激发产生的激子和分子链位移变换的运动规律.α-螺旋是蛋白质二级结构的主要类型之一[3-5],由肽基团(H-N-C=O)组成,均匀地分布在三个氢键上,形成螺旋结构[6-7].一般来说,在Davydov 模型的低阶连续近似下,α-螺旋蛋白中沿着氢键连接的分子动力学可推导出非线性薛定谔方程,如文献[8]中的公式(2.17)、[9]中的公式(3.1).过去对α-螺旋蛋白的动力学行为进行了大量研究,特别是使用简化为单一分子链的单分量模型[10].单一分子链沿着氢键的动力学是在连续极限下考虑的,但忽略了与相邻氢键之间的耦合.实际上,在α-螺旋蛋白模型中,相邻氢键之间的耦合起着重要作用,因此,需要考虑三个螺旋氢键对生物能量传递机制的影响.为更贴切地描述α-螺旋蛋白由三个螺旋氢键组成分子链的形式,文献[11]分析了α-螺旋蛋白分子三个肽通道组成的结构,通过改进的Davydov 哈密顿函数来描述蛋白质分子中的孤子传输机制;文献[12-13]确定了可积分的三分量耦合模型;文献[7,14]考虑了可积耦合的三分量非线性薛定谔方程来描述生物能量沿蛋白质分子链以孤子和呼吸子方式传输的模式;文献[15]利用Hirota 双线性法讨论了三分量非线性薛定谔方程的怪波(rogue wave)传播模式.此外,研究者还在Davydov 模型中引入连续近似中的高阶项[8].文献[16-17]在Davydov-Scott 模型中研究了α-螺旋蛋白中含高阶项的孤子动力学,阐明了Davydov 孤子的稳定性和动态特性.本文将运用三分量高阶非线性薛定谔模型(也称三耦合Hirota 方程)[16-17]研究α-螺旋蛋白中能量输运的怪波模式.考虑α-螺旋蛋白分子动力学高阶项和相互耦合动力学特性后,文献[16-17]给出的方程为

式中: i 为虚数单位;qj=qj(x,t),j=1,2,3为第j个氢键中分子激发的振幅;参数γ是实数;波函数qj加下标t和x分别表示其对时间变量t和空间变量x的偏导数;上标*表示复数共轭.

显然,函数qj(j=1,2,3)都为0,即生物能量不发生输运时,是动力学方程(1)的解.生物能量以孤波方式输运时的解由文献[16]给出;文献[17]讨论了动力学方程(1)孤波的弹性碰撞和非弹性碰撞.本文将考虑周期孤波输运能量的极限状态,采用退化达布(Darboux)变换导出动力学方程(1)的怪波解,讨论极限状态下能量输运的波形演化及其高峰和低谷的极值轨迹.

1 Lax 对表示与达布变换

根据文献[7,16],动力学方程(1)可转换为谱问题[18],其Lax 对(Lax pair)为

式中:λ是复的谱参数;列向量φ=(φ1,φ2,φ3,φ4)T是由势函数φj(j=1,2,3,4)组成的特征函数,这里,上标T 表示转置.

取Lax 对的x部分如下:

其中,0 和I3分别表示零矩阵和三阶单位矩阵,q=(q1,q2,q3),上标†表示Hermitian 转置.

取Lax 对的t部分如下:

则由零曲率方程Ut-Vx+[U,V]=0或协调性条件φxt=φtx可导出动力学方程(1).这里,矩阵交换子[M,N]≡MN-NM.

因此,函数q是动力学方程(1)的解,等价于零曲率方程成立,也等价于Lax 对(2)的特征函数φ满足协调性条件.

即用q[1]替换U0中的q.同时,Vj(j=0,1,2,3)中的U0和q也做相同的替换获得,从而获得V[1].此时,若U[1]和V[1]满足零曲率方程,或等价地,Lax 对

另一方面,考虑作用于Lax 对(2)的规范变换[19]

其中,I4是四阶单位矩阵,S=(sij)4×4,则

满足谱问题

和零曲率方程

于是,引入达布变换T,使得U[1]和V[1]同时满足零曲率方程和Lax 对形式不变,即

从而,由式(9)和(10)关于谱参数λ的各阶系数恒等可得方程组:

这里,式(12)给出了由动力学方程(1)的一组解q通过一次达布变换得到一组新解[1]q的计算公式.接下来将利用某个已知的解q=q[0]和λ及其关联的特征函数φ=φ[0]来构造达布变换中的S矩阵,特别是元素s12,s13,s14的表达式.

当q=q[0]时,记特征函数φj=(φ1j,φ2j,φ3j,φ4j)T是动力学方程(1)在谱参数λ=λj下的解.由λj及其关联的φj构造矩阵Σj和Hj,

则对于任意谱参数λ1∊C R,取

直接计算可以验证,当S=S1时,方程(11a)～(11f)均成立.需要特别指出的是,H1矩阵中的第一列是q=q[0]时动力学方程(1)在λ=λ1时的特征函数,其他几列通常都不是特征函数,而是与第一列复正交的向量.

由式(14)可得S1H1=H1Σ1,或

于是,达布变换中的S1矩阵可以通过方程(15)完全确定.这里,特别地考察待定参数s12,s13,s14所在的的第一列,于是可得线性方程组

简记线性方程组(16)的常数项为

则利用克莱姆法则,由式(12)和(16)可得定理1.

定理1设是动力学方程(1)的解,当q=q[0]时,φ1是Lax 对(2)中谱参数λ=λ1∊C R 关联的特征函数,则一次达布变换的表达式

定理1 给出了从种子解q[0]出发,利用给定谱参数λ1所关联的特征函数φ1构造一次达布变换获得新解q[1]的公式.因此,有了Lax 对的表示形式,动力学方程(1)可以从一组解对 (φ[0],q[0];λ),通过一次达布变换构造另一组解对 (φ[1],q[1];λ,λ1).接着,若以 (φ[1],q[1];λ,λ1)为种子,用新的谱参数λ2(≠λ1),第二次使用达布变换可以构造出另一新解对 (φ[2],q[2];λ,λ1,λ2).将第一次达布变换和第二次达布变换复合,称之为二重达布变换.以此类推,不妨记n重达布变换后的解对为 (φ[n],q[n];λ,λ1,…,λn),其中λj(j=1,2,…,n)互不相等.

利用定理1,可以从种子解0 解出发,生成动力学方程(1)的孤子解(soliton)和退化孤子解(positon)[20],也可以从平面波解出发,生成呼吸子解[21]和退化呼吸子解.本文将以平面波解作为种子解,借助退化的达布变换构造动力学方程(1)的怪波解.

2 怪波的激发条件

在下文中,将取定种子解[0]q为平面波解,即

其中ρj=ajx+bjt,aj,bj,cj∊R,bj满足色散关系:

此时,利用规范变换可将Lax 对(2)变量分离,并进一步给出与种子解关联的特征函数及怪波激发的条件.

则由规范变换φ=Rψ,可得变量已分离的Lax 对

其中多项式系数分别为

由式(24)容易验证,[Λ,Ω]=0,即矩阵Λ,Ω可交换.

设uj(j=1,2,3,4)是矩阵Ω的特征值,则由式(24)可得,矩阵Λ的特征值vj满足

且uj和vj具有相同的特征向量ηj,

其中θj=exp(ujx+vjt)ηj,j=1,2,3,4,则Ψ与exp(Ωx) exp(Λx)等价,都是式(22)的基解矩阵.因此,

是谱参数λ和种子解(j=1,2,3)关联的特征函数,其中,ξ是四维的常数列向量.

两组Lax 对(2)和(22),它们的特征函数通过可逆变换R建立了联系,而它们各自达布变换待求的矩阵S的元素也可以通过可逆变换R建立联系.由于,可得定理2.

定理2若X=S满足线性方程组

则X′=S满足线性方程组

其中,函数H(∙)和β(∙)分别由式(13)和(17)定义.

证明考察线性方程组

用H、β和R来表示这两个线性方程组,可知定理2 成立.证毕.

由于R矩阵的性质和H与β函数构造的矩阵的特点,定理2 给出了Lax 对(22)在其达布变换中求解的s1j与Lax对(2)在其达布变换中求解的之间的比例关系,即,j=2,3,4.因此,接下来将集中讨论Lax 对(22)中特征函数ψ的构造及其s1j的表示.

为了获得呼吸波传播的极限波形态,即怪波解,也称为Peregrine 孤子[22-23]或(准)有理解,本文考虑共振条件,即特征值uj(j=1,2,3,4)趋向同一值而形成四重根的条件.并且利用在规范变换(21)中引入的平移参数u0,将矩阵Ω的特征多项式

的四重根平移到零点.于是,可获得x部分关于怪波激发的条件:

同时,利用平移参数v0将矩阵Λ的特征值平移至零点.于是,可得其中一组怪波激发的条件:

和谱参数λ激发怪波的临界值:

当激发条件式(27)和(28)同时成立时,色散关系式(20)可整理为

3 基础特征函数与退化达布变换

在满足激发条件式(27)的情况下,当λ=λ0时,矩阵Ω,Λ相似于退化的若当块.现考虑λ0引入微扰量,取

考察λ1关联的特征函数.此时,由式(25),对Lax对(22)的特征函数ψ=Ψξ关于∊泰勒展开可得

令常数向量ξ分别为

计算可得一组幂级数的多项分裂(multisection)构成的特征函数:

其 中,φ4j+k=Ψ4j+k ξk(k=0,1,2,3;j=0,1,2,…)是 由关于x,t的多项式组成的向量.

本文称

为Lax 对(2)构造怪波解的基础特征函数组.分别将基础特征函数Rψj作为φ,用于达布变换生成动力学方程(1)的新解.对于新解,考虑λ1→λ0时的极限,即∊→0时动力学方程(1)的极限状态.此时根据定理2 和罗必塔法则,原定理1 可退化为定理3.

定理3设φk=Rψk(k=1,2,3)由式(21)和(32)定义,是动力学方程(1)对应谱参数λ1=λ0+c1∊4和种子解q[0]关联的基础特征函数,则下列用行列式形式表出的函数是动力学方程(1)的一阶怪波解:

证明当极限∊→0时,由罗必塔法则可得,或等价地直接提取分子分母矩阵中每个元素关于∊最低次幂的系数可得.

定理3 考虑了极限情况下的解.在此(准)有理解(34)的表达式中,ψk关联的为有理函数,而因子exp(iρj)来源于定理2 指出的R0.需要说明的是,当k=0 时,也可以根据定理3计算一次达布变换,获得的解依旧为平面波解.

4 怪波的波形演化与极值轨迹

怪波也称为极端波、异常波.为了展示在极限状态下,α-螺旋蛋白的生物能量和生物信息传递动力学性质,本节利用定理3 给出k=1,2,3时一阶怪波解的表达式,讨论参数在不同数值下,尤其是a1为零和不为零时,怪波解各个分量的波形演化和波峰波谷轨迹.

4.1 参数k=1 时的怪波

当k=1 时,三分量高阶非线性薛定谔方程的一阶怪波解为

固定某个时刻t,考察各个分量关于空间变量x的驻点,可得各个分量关于时刻t的极值轨迹.

谷值轨迹为

显然,在t=0时,波形分别在x=(2c1)-1和x=处达到无量纲化的最大值和最小值0.即当t=0 时,有一个三倍于平均振幅的波峰极值出现,且两侧会出现对称的波谷极值.这种剧烈的生物能量传递信号对α-螺旋蛋白的三个氢键的动力学影响有待实验观测和研究.当t→±∞时,波形趋向为一峰二谷形状的孤波,且峰值和谷值都趋向于渐近平面高度

种子解中参数a1是x的系数,a1是否为常数0对波形有显著影响.当a1=0 时,方程(28)可获得孤波解.例如,取a1=0,c1=γ=1,的波形演化如图1 所示,区域[-2,2]× [-4 0,40]是波形的主体部分,其他区域已衰减到渐近平面的邻域.

图1 一阶怪波解各个分量的波形演化(a1=0,c1=γ=1)

其极值轨迹如图1(a)中虚线所示,其中红色虚线是波峰轨迹线,蓝色虚线是波谷轨迹线.观察峰值和谷值的表达式可知,当t=0 时,波形达到了最大值和最小值,分别为3,0,0.

当a1≠0 时,方程(35)可获得时间-空间双局域的怪波解.例如,取a1=1,c1=γ=1时,波函数的波形演化如图2 所示,其中虚线是t时刻极值的轨迹线.两条极值轨迹的表达式是

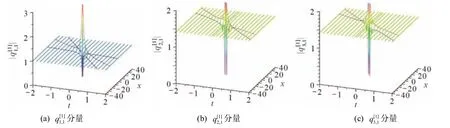
图2 一阶怪波解各个分量的波形演化(a1=1,c1=γ=1)

4.2 参数k=2 时的怪波

当k=2 时,三分量高阶非线性薛定谔方程的一阶怪波解为

其中,

这里,

鉴于k=2 的时候波函数的极值轨迹线是四次多项式的根,在一般情况下,极值轨迹的显式表达式过于繁长,为免赘述,仅在示例中用三维虚线表出.

当a1=0,c1=γ=1时,波函数的波形演化如图3 所示,其中虚线是波峰和波谷所在的极值轨迹线.图示区域[-5,15]× [-3 00,100]是波形的主体部分,其余区域的波形已逐渐衰减到渐近平面的邻域.

图3 一阶怪波解各个分量的波形演化(a1=0,c1=γ=1)

当a1=1,c1=γ=1时,波函数的波形演化如图4 所示,其中虚线是波峰和波谷所在的极值轨迹线.图示区域[-2,2]× [-30,30]是波形的主体部分,其余区域的波形已快速衰减到渐近平面的邻域.

图4 一阶怪波解各个分量的波形演化(a1=1,c1=γ=1)

4.3 参数k=3 时的怪波

当k=3 时,三分量高阶非线性薛定谔方程的一阶怪波解为

其中,

这里,

k=3时,波函数的极值轨迹线是六次多项式的根,在一般情况下,极值轨迹没有显式的根式表达式,文中同样地仅在示例中用三维虚线表出.

当a1=0,c1=γ=1时,波函数的波形演化如图5 所示,其中虚线是波峰和波谷所在的极值轨迹线.图示区域[-5,25]× [-5 00,100]是波形的主体部分,其余区域的波形已逐渐衰减到渐近平面的邻域.

图5 一阶怪波解各个分量的波形演化(a1=0,c1=γ=1)

当a1=1,c1=γ=1时,波函数的波形演化如图6 所示,其中虚线是波峰和波谷所在的极值轨迹线.图示区域[-2,2]× [-3 0,30]是波形的主体部分,其余区域的波形已快速衰减到渐近平面的邻域.

图6 一阶怪波解各个分量的波形演化(a1=1,c1=γ=1)

在上述分别以k=1,2,3给出的示例图中,对比a1=0和a1≠ 0的两种情况可知,a1是否为零对于波形的局域性有显著的影响.当a1≠ 0时,波峰将迅速衰减到渐近水平,波峰观察的窗口期较短.当a1=0时,其波峰衰减速度缓慢,有较长的观察时间.

文中波形不同于文献[16-17]展现的孤波,文献[16-17]的2-孤子在不同参数下展现了两孤波之间的弹性碰撞和非弹性碰撞,长时间内波高恒定的孤波容易被观察到,且孤波碰撞的强相互作用区域容易被预测,本文讨论的怪波的波高不定,波峰振幅巨大,是一种极限形态,这给α-螺旋蛋白激发孤波传递生物能量和生物信息提供了一种新的理论形态.

5 结论

本文研究了α-螺旋蛋白中生物能量沿蛋白质分子链以孤波方式传输的三分量高阶非线性薛定谔方程的控制模型,讨论了该模型中三个相互耦合的波函数在极限状态下激发极限波的形态,即怪波解.基于控制模型Lax 对表示的谱问题,文中给出了以下三点发现:

(1)利用规范变换得到了三分量高阶非线性薛定谔方程的达布变换,该变换借助谱参数为某个任意给定的值及其所关联的特征函数,构造线性方程组,并利用克莱姆法则,通过行列式形式表出.

(2)通过Lax 对的变量分离和平移参数的引入,给出了怪波激发的一组代数条件,其中包括谱参数的临界值.通过对谱参数临界值的微扰,利用幂级数的多项分裂构造怪波解的基础特征函数,并由此导出了退化的达布变换.

(3)平面波解通过退化的达布变换获得三分量高阶非线性薛定谔方程的怪波解.在不同的参数下,用三维图形示例怪波解的波形演化及其极值轨迹,其中包括时间-空间双局域的怪波.极值轨迹表明了多个耦合分量之间能量分布和传输模式的不同.

本文方法和分析结果为三分量高阶非线性薛定谔方程控制的α-螺旋蛋白中生物能量传输的怪波激发实验研究提供了理论支持,促进了对怪波产生机制和形成效果的理解.特别地,当参数γ等于0 时,控制模型退化为光学中重要的Manakov系统,在光通信的研究中也具有重要的实际意义.