基于犹豫模糊集的水质评价方法
曹 磊,戴俊杰,毛小燕*,蒋 吉,刘锋琴
(1.宁波大学 信息科学与工程学院,浙江 宁波 315211;2.宁波大学科学技术学院 信息工程学院,浙江 宁波 315300;3.慈溪市水利局,浙江 宁波 315399)
随着人类社会经济的飞速发展,水环境污染以及水生态退化等问题日益明显,严重违反了可持续发展理念,背离了习近平同志“绿水青山就是金山银山”的重要论断.因此加强水环境治理已经成为各省政府的当务之急,而其中对水质的评价是所有事项中的重中之重,只有对水质观测数据进行合理有效的评价才能引导制定科学有益的防治对策.从这方面来说,水质综合评价的合理性将直接影响管理者的决策[1-2].
目前,国内外常见的水质评价方法有单因子评价、神经网络评价、模糊综合评价等.单因子评价是指采用目标水体中所有参与综合评价的水质指标,选取其中最差的水质单项指标所属的类别作为该目标水体的类别[3],其对水质的要求过于保护,无法客观地反映水体的综合状态.人工神经网络(Artificial Neural Networks)是一种模仿动物神经网络行为特征,通过调节内部大量节点参数及其权重信息从而实现其拟合函数、处理信息等功能的算法.早在20 世纪末,就已经有学者将模型结构运用到水质评价任务中[4-5].虽然神经网络具有很好的客观性,精度也相较于其他方法要高,但其训练过程需要大量带标签样本数据,且特征选取会极大地影响最终模型的效果.近几年也有学者对神经网络予以改进,用于水质评价研究[6-7],但也不能达到令人十分满意的效果.由于水质评价是一个多指标影响的复杂过程,且对污染程度的分级界限较为模糊,传统方法很难刻画这种不确定性,而模糊集理论为解决此类不确定性问题提供了新思路.模糊综合评价[8]关键在于隶属函数和指标权重的确定,常通过构造高斯隶属函数[9]或梯形隶属函数[10]来确定监测数据与各等级间的隶属度,有效地解决了评价标准边界模糊问题;而权重的确立方法主要有熵权赋值法[11]、超标倍数法[12]及层次分析法[13].在实际应用中,决策者在确定各属性隶属度值时,常会遇到多个数值之间难以取舍的问题.为处理这类情况,Torra 等[14-15]提出了犹豫模糊集概念,其允许选定多个数值作为隶属度,能够更真实地体现决策者犹豫不决的心理.因此本文也首次将犹豫模糊集应用到水质评价领域.
本文采用一种基于犹豫模糊集的水质评价模型,并提出一种新的基于线性插值的悲观补齐方案,根据距离测度来评价水质等级.通过浙江省部分水库的实际算例,进行稳定性和有效性检验,以期丰富水质评价方法,为水资源监管提供客观科学依据.
1 指标筛选
研究数据来源于浙江省生态环境厅公布的地表水水质自动检测数据.根据国家《地表水环境质量标准》(GB 3838—2002)规定,基本的水质评价指标有24 项.但由于指标过多且存在对评价结果参考意义较小的指标,因此需先对指标进行筛选和处理.
挑选慈溪市7 处水体,采集共计10 个月的监测样本,并收集相应的水质等级数据.水体成分和外界环境因素(下文称为特征)具体包含: 水温、pH值、溶解氧、高锰酸盐、总磷、总氮、硫化物等;对应的水质等级分别为1 级至6 级,等级越低表示水质越好,其中,6级表示水质指标严重超标,又称劣V 类,即超出地表水环境质量标准规定的五类水质.首先初步剔除那些存在缺失值以及无任何参考价值的特征(如气温、水温等),接着计算每个特征与水体等级之间的相关系数.水质特征及等级具体结果见表1.
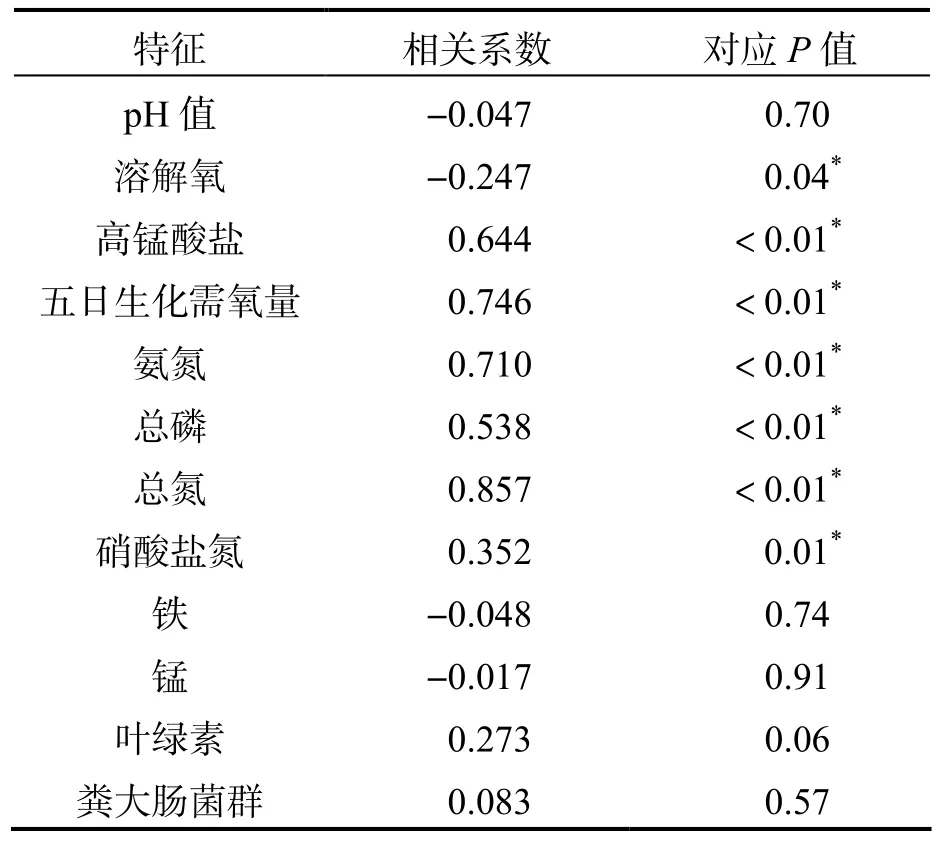
表1 水质特征与水质等级的相关分析
通过相关性分析筛选出7 项显著相关特征.特征与水质等级之间存在相关性,各特征之间也同样存在高度相关性,比如“溶解氧”与“五日生化需氧量”以及“氨氮”与“总氮”.为避免选择的特征之间相关性过高,通过查阅相关文献,并结合《浙江省水资源公报》分析各水库近年来的水质状况,最终选取溶解氧(DO)、高锰酸盐指数(CODMn)、总磷(TP)和氨氮含量(NH3-N) 4 项监测数据作为本文水质评价指标,并且以《地表水环境质量标准》(GB 3838—2002)作为评价依据(表2).
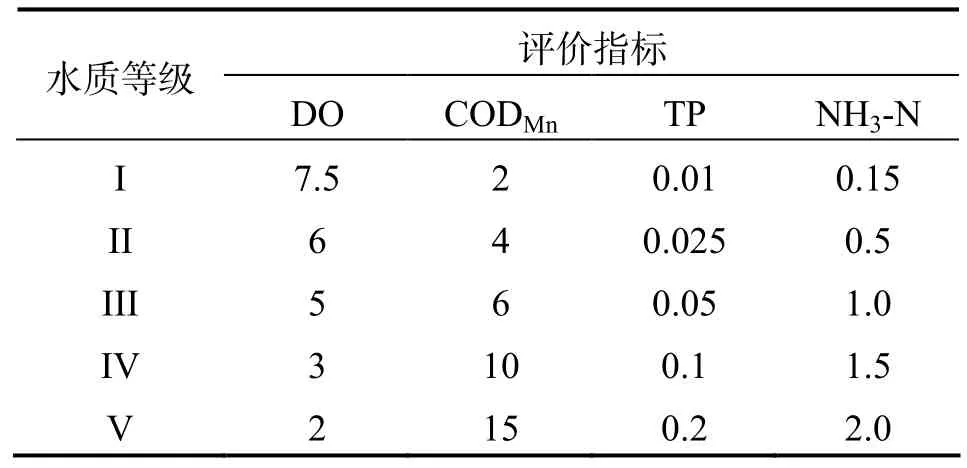
表2 地表水环境质量标准 mg·L–1
2 评价方法
首先构建水质的犹豫模糊标准评价矩阵,在《地表水环境质量标准》(GB 3838—2002)基础上,采用专家打分值建立犹豫模糊矩阵,再通过犹豫模糊指数熵来计算各指标间权重,采用升维补齐方式统一犹豫模糊数的维度,最后使用加权犹豫模糊兰氏距离测度方法计算参评水域犹豫模糊矩阵与标准评价矩阵各等级的距离,最终根据距离最小原则划定水质等级,从而得出水质评价结论.
2.1 水质评价标准矩阵的建立
犹豫模糊集定义: 设论域X={x1,x2,…,xn},则X上的犹豫模糊集(Hesitant Fuzzy Set,HFS)定义为,其中hM(x)为犹豫模糊数,是[0,1]中一些数值的集合,表示集合X中的任一元素x对集合M的隶属度.特别地,如果各犹豫模糊数有且仅有一个隶属度值,那么犹豫模糊集退化为普通的模糊集.
水质评价指标的属性集合X={溶解氧,高锰酸盐指数,总磷,氨氮},并设置5 个不同等级,即等级属性集合为G={优,良,一般,较差,差}.邀请3 名水环境评价方面专家组成水质评价小组,参照表2 规定的各水质指标值,对溶解氧、高锰酸盐指数等评价指标进行打分,分值在0~1,且分值越高代表水质等级越高.最后对评价小组的分值进行合并,形成水质评价标准矩阵.由于不同专家可能有不同的专业知识、背景和偏好,导致分值可能存在差异;但每位专家的意见都需被考虑,因此水质评价标准矩阵中的每个指标值用犹豫模糊数表示为专家打分值组成的集合(表3).
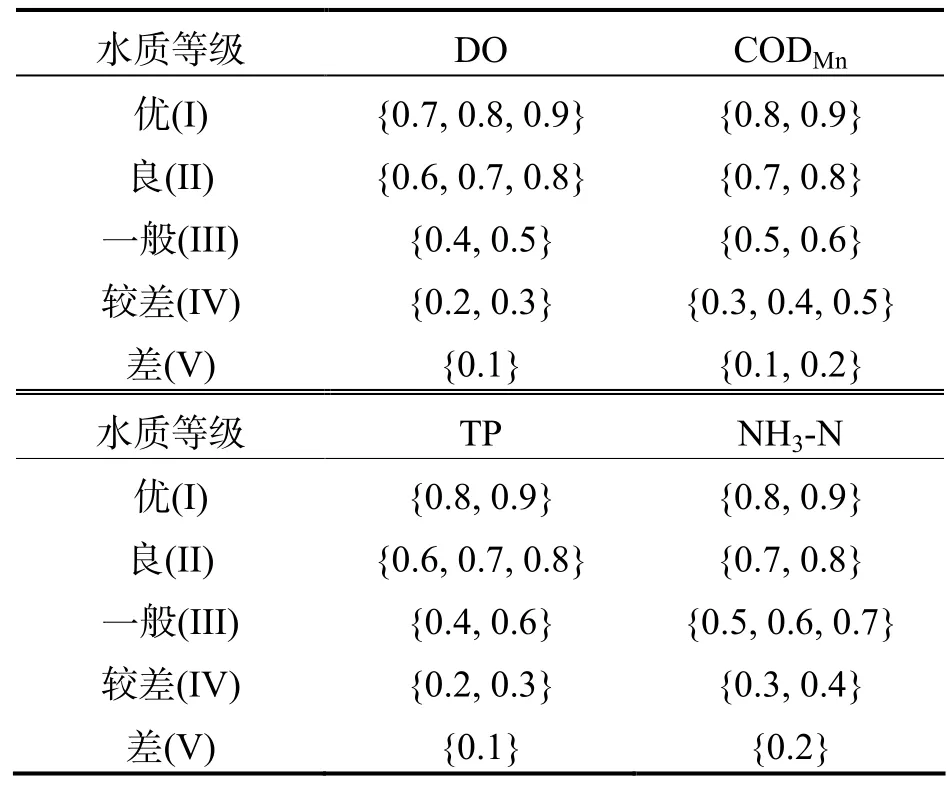
表3 水质评价标准矩阵
2.2 指标权重计算
在指标权重信息未知的条件下,通常需要人为主观给出.本文通过实际数据信息构造犹豫模糊指数熵的方式来确定指标权重,避免了过多人为主观因素的影响.
定义一组犹豫模糊数:
根据定义计算犹豫模糊指数熵,运用信息熵最小化原则计算确定属性权重:
2.3 距离测度计算
对于任意集合X={x1,x2,…,xn}上的犹豫模糊集M和N,距离测度d(M,N)需满足以下性质:
常用距离测度的方式有多种,如豪斯道夫距离测度、海明距离测度、兰氏距离测度[17].本文水质评价中,不同专家对参评水库打分可能会出现一定差异性,如当遇到评价指标存在偏倚较大的数据,就会导致最终的评价结果偏离真实情况.因此本文将采用兰氏距离进行测度分析,因其是无量纲,并且是采用比值方式来衡量数据之间的距离,减少了极端值的影响,能有效避免上述问题对评价结果的影响.
在进行距离测度计算时,常会遇到犹豫模糊评价矩阵与水质评价标准矩阵在各指标下隶属度不等长的情况,导致无法直接进行距离度量.此时通常都会采用升维或降维的方式将犹豫模糊数长度统一,但降维方式会丢失过多的专家打分信息,因此这里选择采用升维补齐方案,将长度略短的犹豫模糊数补齐至更长的犹豫模糊数.补齐数据的方式也有多种,如对情境乐观的乐观补齐法,可选用犹豫数中最大的隶属度进行补齐;偏向于规避风险的悲观补齐法,可挑选犹豫数中最小的隶属度进行补齐[18].本文认为虽然补齐方式可以很大程度上保留专家们的可靠评价,但是无论是乐观补齐法还是悲观补齐法都未能较好地权衡所有专家之间的意见,鉴于水质评价是一个需要严格把关的问题,因此悲观倾向是能够被采纳的.
所以本文提出基于线性插值的悲观补齐法,它能很好地全面考虑各个专家之间的态度.具体操作如下: 设定一组犹豫模糊数和升维大小d,其中lxi≤d.为保证补齐方法偏向于悲观,从hM(xi)中选取最小的两个隶属度,且,并且在两者之间按照一维线性插值法插入共d-个隶属度,从而达到补齐的效果.
在水质评价的实际运用中,经常会出现不同参评水库有着相同犹豫模糊数的情况.例如一个6名专家组成的评价小组对甲、乙水库的某项水质指标等级进行打分,假设其中专家小组对甲水库的评分情况为4 名专家评分是0.8,另外2 名专家评分是0.6,用犹豫模糊数{0.6,0.8}表示评分值;专家小组对乙水库评分情况为3 名专家评分是0.8,另外3 名专家评分是0.6,用犹豫模糊数{0.6,0.8}表示评分值.虽然甲、乙水库的评价结果完全相同,但显然不符合实际的评分情况.因此,需引入加权犹豫模糊数概念,对犹豫模糊数中每个隶属度值都进行加权处理,且权重大小能反映出每个隶属度的重要程度.但加权的犹豫模糊数也分为专家权重已知和未知两种情形.在专家权重已知情况下,构造加权犹豫模糊数,设专家e1,e2,…,ep对应的权 重向 量wq=(w1,w2,…,wp)T,其 中,wk≥ 0,且
构造加权犹豫模糊数为:
但在绝大多数情况下,专家权重是未知的,此时则令每位专家权重都相同,结合加权犹豫模糊数概念,可给出加权犹豫模糊兰氏距离公式.
假设任意xi∊X的权重为wi,其中i=1,2,…,n,并满足wi∊ [0,1],,则加权犹豫模糊兰氏距离[19]:
由此运用加权犹豫模糊兰氏距离测度方法计算犹豫模糊矩阵与标准评价矩阵的距离,并根据距离最小原则可以得出最终结论.
3 实际应用
使用上述方法对浙江省部分水库水体进行水质评价,并对评价结果进行有效性检验,最后再与其他评价方法进行对比检验.
3.1 算例
出于保护水资源的战略选择,现对浙江省内5处(编号为A、B、C、D、E)水体进行各自的水质量评价.为保证评价结果的可靠性和专业性,邀请8 名水环境评价方面的专家,并根据5 处水体的各自情况分别进行打分评价,整理得到各水体的犹豫模糊评价矩阵,其相关数据见表4.
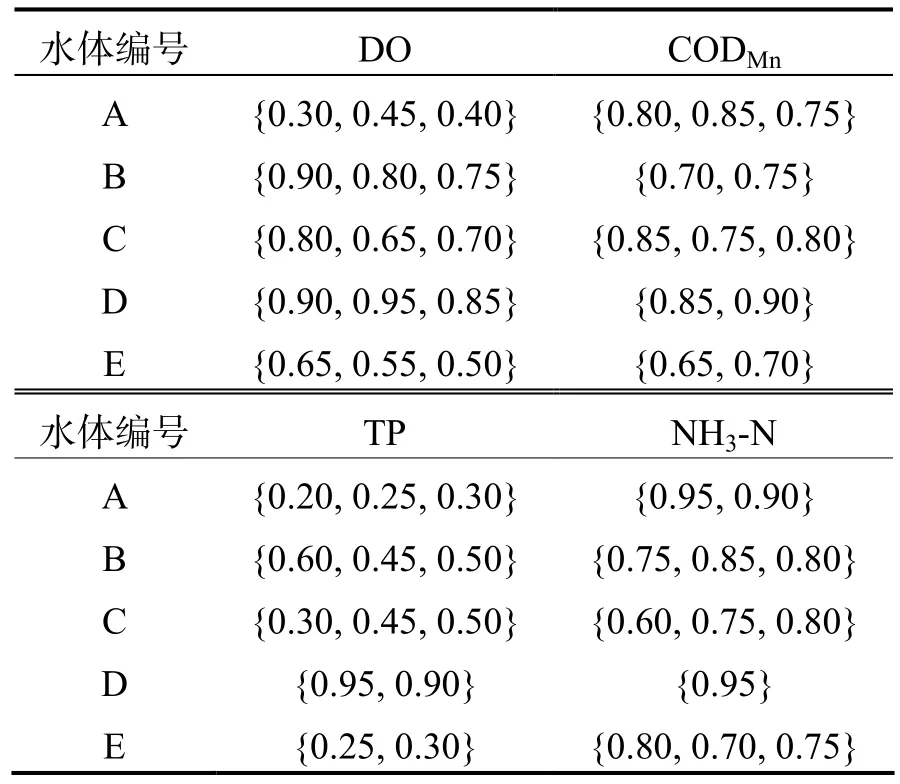
表4 犹豫模糊评价矩阵
根据表4 的犹豫模糊评价矩阵,利用式(1)计算出各水体指标的犹豫模糊指数熵.其中,以水体A 为例:
在得到水体A 在DO 指标上的犹豫模糊指数熵后,同理可构建出各水体相关指数的犹豫模糊指数熵矩阵,其相关数据见表5.

表5 犹豫模糊指数熵矩阵
接着可进一步计算出每个水体在单个指标上的平均模糊熵.再以表5 中DO 指标为例:
其中,E1表示第1 个指标DO 的平均指数熵.同理可得其余3 项指标的平均指数熵分别为E2=0.683(CODMn),E3=0.754(TP),E4=0.534(NH3-N).
通过每个指标模糊熵在总体上的占比,可以得到各个指标的具体权重数值.同样,以DO 指标为例,并依照式(2)可得:
同理可得,w2=0.24(CODMn),w3=0.19(TP),w4=0.36(NH3-N).
由于5 处水体的犹豫模糊评价矩阵与水质评价标准矩阵在各指标下的隶属度不等长,导致无法直接进行距离测度计算,因此需要分别对表3 和表4 进行升维处理.升维后的矩阵数据分别见表6和表7.
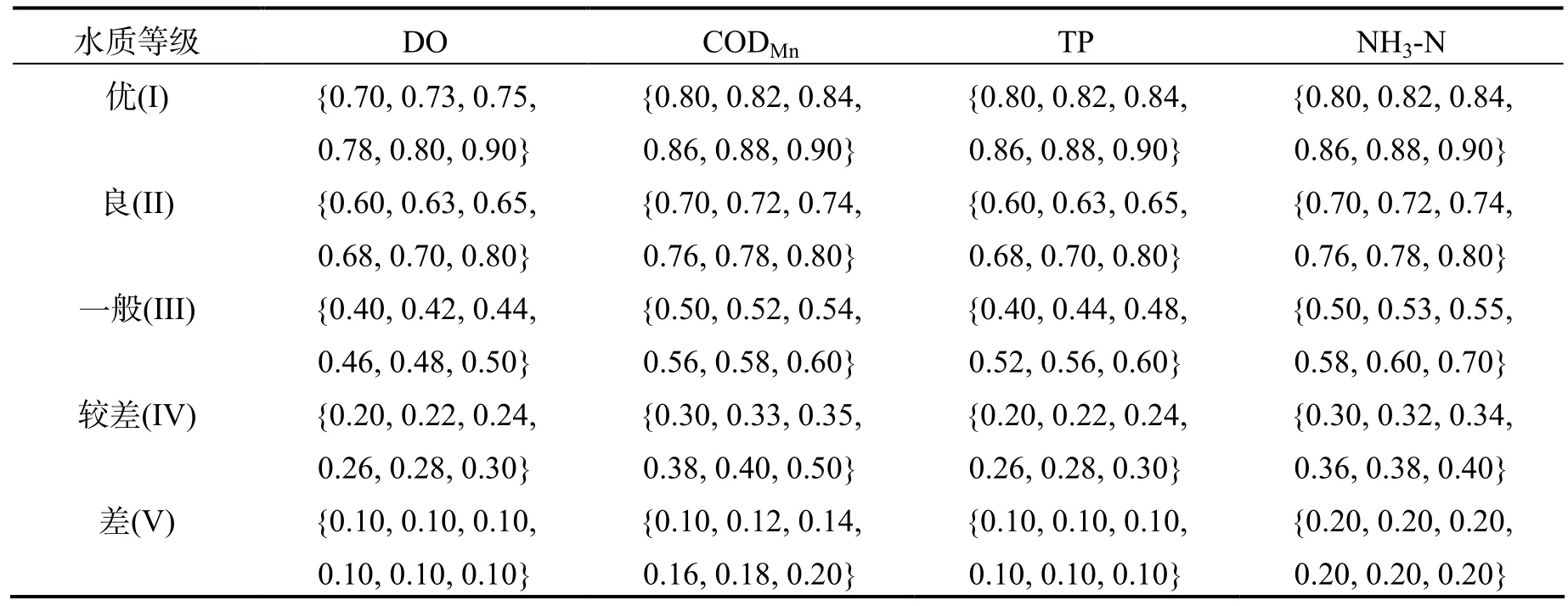
表6 升维后的水质评价标准矩阵

表7 升维后的犹豫模糊评价矩阵
最后根据式(3)计算各水体与各评价等级之间的距离测度,其结果见表8.由最小距离原则,本文将测度最小的等级作为该水体的等级评价,最终各水体的水质评价结果见表9.从表9 可以看出本文评价结果与官方评价结果基本一致,仅A 水体的评价等级与官方出现差异,但对于A 水体来说,从表8 可以看出,距离“良(II)”等级的距离为0.239 6,距离“一般(III)”等级的距离为0.223 0,两者相差仅0.016 6,因此不论从后续改进还是总体准确性来说,本文方法都具备较好的可靠性.

表8 各水体与各评价等级之间的距离测度

表9 各水体的水质评价结果
3.2 稳定性分析
为验证本文评价方法的稳定性,现将上述5 个水体另外相邻3 d 的监测数据和对应的官方评价等级依次进行上述步骤处理,最终得到本文的评价等级,结果见表10.
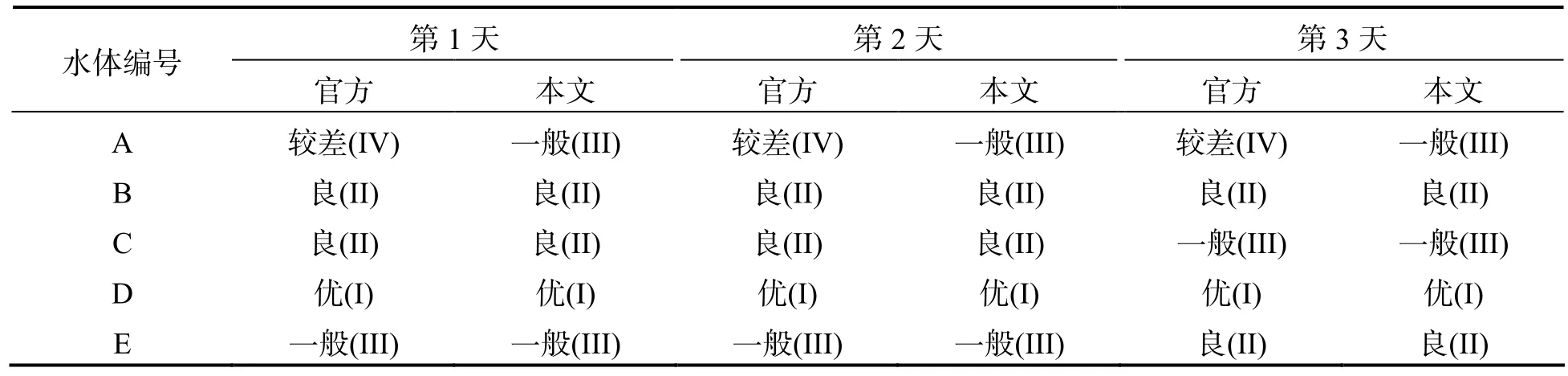
表10 各水体连续3 d 的水质评价结果
从表10 可以明显看出,水体在相邻时间点的水质变化不明显,并且本文的评价等级与官方评价等级基本一致,还能在不同时候保持两者的高度一致性,这也同样说明了本文方法的稳定性.
3.3 有效性分析
采用水质评价领域常用的BP 神经网络和模糊综合评价方法来验证本文方法的有效性,其最终对比结果见表11.

表11 不同方法水质评价结果
根据表11 的对比结果可以看出,BP 神经网络在水质评价中的结果与官方之间存在一定差异,并且神经网络的训练需要大量带标签数据,同时网络输出值也并非是离散值,而是连续值.因此如果取舍不恰当,容易造成最终结果的偏差.而模糊综合评价则与官方评价出入较大,因其仅考虑一位专家的评价,虽简单方便,但也容易导致大量极端值的出现,从而导致结果可信度的缺失.综上所述,本文方法还是具有一定的优越性.
4 结论
水体环境监测是重要的民生大事,是关乎推动建设美丽社会开展的极大事宜,科学全面的水质量评价是其中的重要环节.本文通过筛选有效的水质评价指标,建立水体质量评价体系,并采用线性插值的悲观补齐方案和兰氏距离测度方法,提出一种针对水体质量评价的方法,通过自身和对比检验验证了其稳定性和有效性,以期为日后的水质评价提供一定的参考.

