压电集成石墨烯增强功能梯度多孔板的等几何建模与分析

刘庆运, 刘康仁, 张红一, 刘 涛,2

(1. 安徽工业大学 机械工程学院,安徽 马鞍山 243002; 2. 上海大学 机电工程与自动化学院,上海 200072)

将压电材料与梁、板、壳等基体结构相结合所形成的压电智能结构常被应用于航空航天等领域[1]。目前,常见压电智能结构的基体材料大多以金属材料[2]、聚合物材料[3]、功能梯度材料[4]和正交铺设的层合材料[5]为主。近年来,科学技术,尤其是新一代航空航天技术的飞速发展也对航空航天装备在高性能、轻量化、长寿命等方面提出了更高的要求。在压电智能结构中,压电材料的尺寸和重量相对于基体材料可以忽略不计。因此,基体结构的材料选择和几何设计成为了压电智能结构轻量化设计的主要方向。多孔材料[6-7](例如金属泡沫材料),因具有质量轻、强度高等优点,为压电结构基体材料的选择提供了一种新的可能。另外,多孔材料中的孔隙常被设计为沿某一或多个方向上呈梯度分布,所形成的功能梯度多孔材料的力学性能在特定方向上也呈连续梯度分布,具有良好的抗冲击性能[8]。因此,以功能梯度多孔材料作为压电智能结构的基体材料,可以保证结构在具有较高刚度的同时有效地降低结构的质量。但研究表明,基体材料内部孔隙的不断增大会导致结构的刚度不断减小[9]。

碳纳米材料,如一维碳纳米管(carbon nanotubes, CNTs)[10-11]和二维石墨烯纳米片(graphene platelets, GPLs)[12-13],具有低密度、高强度及优异的抗疲劳特性等优点,使其成为复合材料理想的增强体。试验表明相比于CNTs,GPLs具有更大的比表面积,可以更有效地与基体材料结合,大幅度增强复合材料的机械性能[14-15]。目前,已有部分学者对石墨烯增强功能梯度多孔梁、板、壳结构的建模方法进行了研究。为书写方便,本文将石墨烯增强功能梯度多孔材料简写为GPLs-FGP,压电集成石墨烯增强功能梯度多孔材料简写为P-GPLs-FGP。Kitipornchai等[16-17]利用Timoshenko梁理论建立了GPLs-FGP梁的线性和非线性理论模型,并研究了梁的振动和屈曲行为。基于经典理论(classical theory, CT)。Li等[18]构建了GPLs-FGP壳结构的热弹性屈曲模型。针对GPLs-FGP板结构,Gao等[19-20]分析了Winkler-Pasternak弹性基础上GPLs-FGP板的非线性振动响应。采用伽辽金法,Teng等[21]基于CT探索了GPLs-FGP薄板的非线性强迫振动响应,Xu等[22]则基于一阶剪切变形理论(first-order shear deformation theory, FSDT)提出了一种热屈曲解析解模型。Arshid等[23-24]采用广义微分求积法建立了GPLs-FGP板的热屈曲数值分析模型。Yang等[25-26]利用无网格法和Chebyshev-Ritz法分析了GPLs-FGP板的屈曲和自由振动问题。相对而言,有限单元法仍是GPLs-FGP结构数值法建模的主要手段之一,利用有限单元法,Li等[27]分析了GPLs-FGP圆柱壳在径向载荷作用下的静力学响应;Genao等[28]基于高阶剪切变形理论(higher-order shear deformation theory, HSDT)建立了机-热载荷下GPLs-FGP微尺度板的非线性有限元模型;Nguyen等[29]则基于HSDT和一种多边形有限单元法对GPLs-FGP板的自由振动进行了分析。此外,Li等[30]和Nguyen等[31]先后利用等几何分析(Isogeometric analysis, IGA)方法建立了GPLs-FGP板的数值分析模型,并研究了板的固有频率、静态弯曲和屈曲响应。在他们的研究中,Li等采用的是FSDT和Reddy’HSDT,而Nguyen等采用的是一种仅包含3自由度的HSDT,但该理论要求基函数至少C3连续。

上述研究工作表明将少量的GPLs填充到多孔材料中,所形成的石墨烯增强的功能梯度多孔材料可以在保留多孔材料轻质性的同时,有效地解决因孔隙增加所引起的结构刚度减小问题。因此,GPLs-FGP材料成为了压电智能结构基体材料的重要选择之一。Al-Furjan等[32]建立了微尺度P-GPLs-FGP圆柱壳结构的解析解模型。Moradi-Dastjerdi等[33]结合HSDT和无网格方法分析了弹性基础上P-GPLs-FGP板的屈曲响应。Nguyen等[34-35]则基于HSDT和IGA方法建立了P-GPLs-FGP板的线性和非线性模型,并对板的静力学、动力学和主动振动控制问题进行了研究。

由上述文献可知,目前板、壳结构的数值建模方法大多采用CT,FSDT和HSDT。其中,CT仅包含3个未知变量,计算效率相对较高,但其忽略了横向剪切变形,只适用于分析尺寸较薄的结构。FSDT包含5个未知变量,其考虑了横向剪切变形,但在结构较薄时会因无法满足Kirchhoff假设而出现剪切自锁的现象,因此仅适用于中等厚度板、壳结构的分析。HSDT相对较为准确,但其未知变量一般大于等于5个,且离散化过程较为复杂。此外,在压电智能结构中,压电材料的机电耦合特性使得结构的建模和分析变得更为复杂。因此,建立数值分析模型时所选择的板、壳理论直接影响着结构分析的准确性和高效性。

值得注意的是,Thai等[36-37]提出了一种简化一阶剪切变形理论(simple first-order shear deformation theory, S-FSDT),该理论由一阶剪切变形理论推导而来,在分析薄板时,S-FSDT自动退化为经典理论,从而满足Kirchhoff假设。在分析中等厚度板时,该理论既考虑了剪切变形且仅含有4个未知变量,具有较高的计算精度和计算效率,但其要求位移场插值函数满足C1连续性。作为一种新兴的数值方法,IGA方法的基本思想是将计算机辅助设计(computer aided design,CAD)的NURBS基函数直接作为有限元分析的形函数,利用样条的控制节点作为计算网格节点,从而在表达上使CAD与CAE获得统一。因此,IGA方法具有几何精确、精度高、鲁棒性好、无需传统的网格划分过程等优点。此外,NURBS的高阶连续性恰好可以满足S-FSDT的C1连续性这一要求。

根据上述分析,本文首先结合IGA方法和S-FSDT建立了集成电层的石墨烯增强功能梯度多孔板的数值分析模型,在结构基体材料中孔隙与石墨烯的都具有非均匀对称分布、非均匀非对称分布和均匀分布3种分布形式;其次,通过与已有文献进行对比验证了本文模型的准确性和有效性;最后,利用该模型详细分析了孔隙分布形式、孔隙系数、石墨烯分布模式、石墨烯质量分数以及板的宽厚比和边界条件对结构自由振动和静态弯曲响应的影响。

1 P-GPLs-FGP板的等几何分析模型

如图1所示,P-GPLs-FGP板的长度为a,宽度为b,中间层是厚度为hc的GPLs-FGP板,上、下层是厚度为hp的压电层,结构的总厚度h=hc+2hp。

图1 压电集成石墨烯增强功能梯度多孔板Fig.1 Piezoelectric integrated graphene platelets reinforced functionally graded porous plate

1.1 GPLs-FGP材料的有效属性

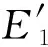
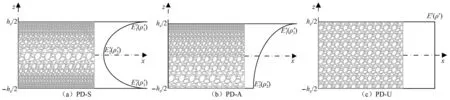
图2 孔隙分布方式Fig.2 Types of porosity distribution

中间层GPLs-FGP板的弹性模量、剪切模量和密度可表示为

(1)

式中:E*,ν*和ρ*分别为无孔隙时复合材料的有效弹性模量、泊松比和密度;e0为孔隙系数;em为密度系数,分别表示为

(2)

(3)

φ(z)为孔隙分布函数,对应图2所示的3种孔隙分布形式,表示为

(4)

根据高斯随机场(Gaussian random field, GRF)理论,多孔材料的弹性模量与密度之间存在如下关系

(5)

将式(1)代入式(5),得到

(6)

同样根据闭胞体GRF理论[38],GPLs-FGP材料的泊松比ν(z)可表示为

ν(z)=0.221p′+ν*(0.342p′2-1.121p′+1)

(7)

式中,ν*为不含孔隙时石墨烯增强基体材料的泊松比。

(8)

根据改进Halpin-Tsai微观力学模型,无孔隙时石墨烯增强功能梯度材料的弹性模量E*为

其中,

(10)

式中:wGPL,lGPL和tGPL分别为石墨烯纳米片的平均宽度、长度和厚度;EGPL和Em分别为石墨烯和基体的弹性模量。

与孔隙分布类似,石墨烯同样具有三种分布模式,非均匀对称分布GPL-S、非均匀非对称分布GPL-A和均匀分布GPL-U,如图3所示。不同分布模式下,石墨烯沿厚度方向的体积分数为

图3 石墨烯分布模式Fig.3 Dispersion patterns of GPLs

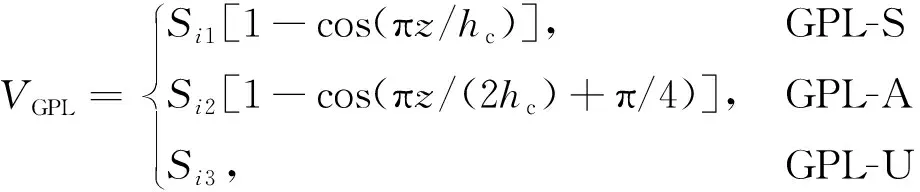
(11)

式中,Si1,Si2和Si3为石墨烯体积分数的最大值,i=1,2,3分别为PD-S,PD-A和PD-U 3种孔隙分布形式。每一种孔隙分布都可以与3种不同的石墨烯分布模式相结合,因此,本文共有9种不同的组合形式。Si1,Si2和Si3可以根据石墨烯的体积分数VGPL和质量分数WGPL的关系(见式(12))计算得到。

(12)

假设不同孔隙分布和石墨烯分布模式下,GPLs-FGP板的质量M相等,则M可定义为

(13)

根据式(5),可以得到孔隙均匀分布时(PD-U)的孔隙系数

(14)

最后,根据复合材料混合定律,石墨烯增强复合材料的密度和泊松比可表示为

ρ*=ρGPLVGPL+ρmVm

(15)

ν*=νGPLVGPL+νmVm

(16)

式中:ρGPL,νGPL和VGPL分别为石墨烯的密度、泊松比和体积分数;ρm,νm和Vm= 1-VGPL分别为基体的密度、泊松比和体积分数。

1.2 简化一阶剪切变形理论

根据一阶剪切变形理论,可得到板的位移场为

(17)

式中:u0,v0,w0分别为x,y,z方向上的中面位移;βx和βy分别为中面法线绕y轴和x轴的转角。

在分析薄板时,一阶剪切变形理论会因无法满足Kirchhoff假设出现剪切自锁现象。本文采用的简化一阶剪切变形理论是由一阶剪切变形理论推导而来。首先将式(17)中的挠度w0分解为弯曲挠度wb和剪切挠度ws两项,即w0=wb+ws;其次,将转角变量分别由弯曲挠度对坐标的导数表示,即βx=-∂wb/∂x,βy=-∂wb/∂y。因此,简化一阶剪切变形理论的位移模式可表示为

(18)

在分析薄板时,剪切挠度ws可以忽略,从而满足Kirchhoff假设,有效消除剪切自锁现象。在分析中等厚度板时,简化一阶剪切变形理论既考虑了剪切变形,又仅包含4个未知变量(u0,v0,wb,ws),可以在保证精确性的同时提高计算效率。

式(18)可改写为

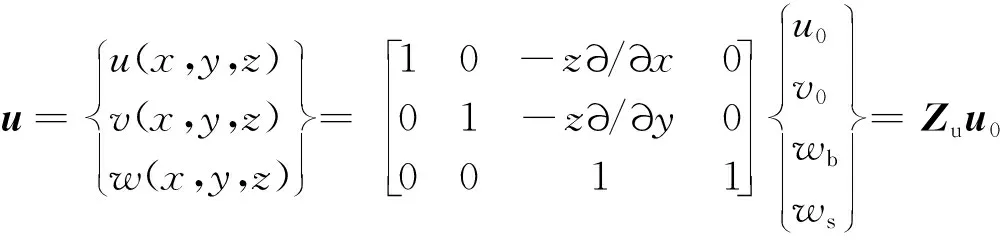
(19)

其中,

(20)

根据几何方程,应变-位移关系可表示为

(21)

式中,

(22)

广义应变S为

(23)

式中,

(24)

1.3 本构方程

对于上、下层的压电材料,其本构方程为

(25)

式中:σ和ε为应力和应变向量;Q为弹性系数矩阵;E为电场强度向量;D为电位移向量;e和g分别为压电应力常数矩阵和介电常数矩阵。

弹性系数矩阵Q的定义为

(26)

其中,

(27)

压电应力常数矩阵和介电常数矩阵分别为

(28)

(29)

本文仅考虑外部电场沿z轴方向的作用,并假设压电层的每一个单元只有一个电自由度,因此,电场可表示为

E=-∇φ=Bφφ

(30)

其中,

(31)

1.4 等几何分析

二维NUBRS样条基函数是由两个一维B样条基函数的张量积组成,可表示为

(32)

式中:wi,j为权因子;Bi,p(ξ)和Bj,q(η)分别为ξ方向上的p阶和η方向上的q阶B样条基函数。

利用NURBS基函数,板的机械位移场可表示为

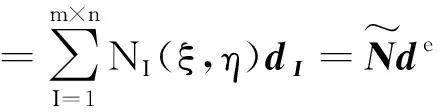
(33)

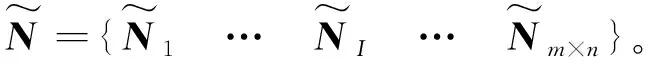
(34)

将式(34)代入式(24),广义应变S可改写为

(35)

其中,

(36)

(37)

(38)

1.5 控制方程

利用哈密顿变分原理(见式(39)),可推导出板结构的弱形式。

(39)

式中:t1和t2为起始和结束时间;L为总能量,包括动能T、势能U和外力所做的功Wext。式(39)可展开为

(40)

将式(19)、式(25)和式(33)代入式(40),并对单元进行组装,得到P-GPLs-FGP板的运动控制方程为

(41)

式中:Muu为质量矩阵;Kuu为机械刚度矩阵;Kφφ为压电材料自适应刚度矩阵;Kuφ和Kφu为机电耦合刚度矩阵;f为机械载荷;fφ为压电层表面的电荷面密度等效控制电量。其具体表达式为

(42)

其中,

(43)

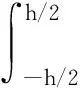
(44)

(45)

(46)

(47)

2 算例分析

本章,首先通过分析GPLs-FGP板的固有频率和P-GPLs-FGP板在机-电载荷作用下的静态弯曲响应,对本文等几何分析模型的有效性和准确性进行验证。在此基础上,分析了孔隙系数、孔隙分布形式、石墨烯质量分数、石墨烯分布方式、宽厚比和边界条件对P-GPLs-FGP板的固有频率和静态弯曲响应的影响。本文所有数值算例的NURBS基函数阶次均为p=q=3,网格密度均采用17×17。为方便起见,机械边界条件简写为:简支(S),固支(C),自由(F)。如未特殊说明,板的材料参数如表1所示。

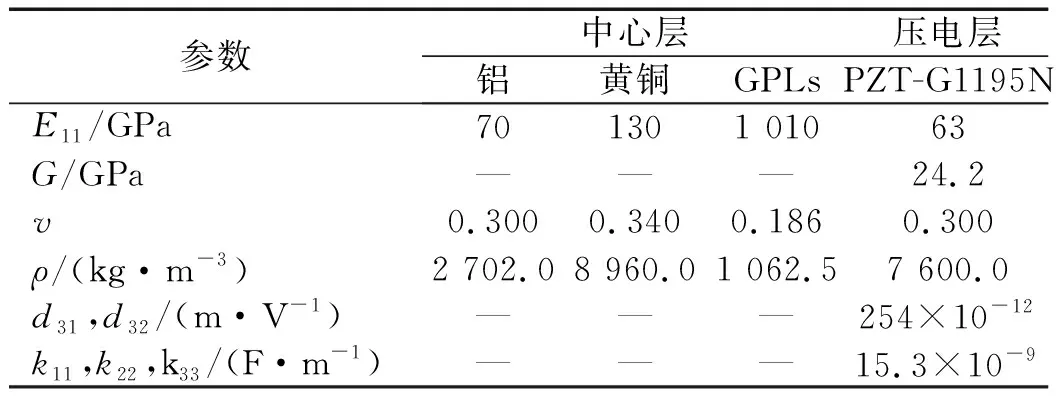
表1 材料参数Tab.1 Material parameters

2.1 验证性分析

2.1.1 GPLs-FGP板的固有频率分析

一个四边简支板(SSSS)的尺寸为a=b=1 m,h=0.005a,hp=0.1h,hc=0.8h。上、下层为铝,中心层为铝基GPLs-FGP材料,孔隙和石墨烯都为均匀分布(PD-U, GPL-U)。石墨烯与孔隙的参数为lGPL=2.5×10-6m,wGPL=1.5×10-6m,tGPL=1.5×10-9m,WGPL=1.0%,e0=0.5。表2为板的第1、第5、第11和第21阶固有频率。可以看出,本文结果与Li等的解析解结果和Nguyen等基于HSDT的等几何分析结果较为接近,这验证了本文方法对于石墨烯增强功能梯度多孔板固有频率分析的有效性和准确性。

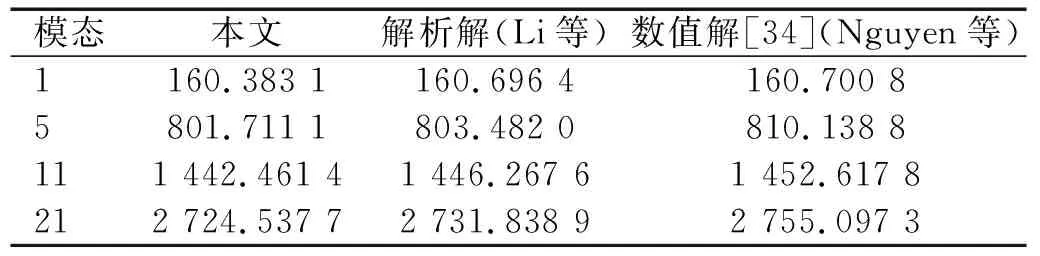
表2 GPLs-FGP板的固有频率Tab.2 Natural frequency of the GPLs-FGP plate

2.1.2 P-GPLs-FGP板的静态弯曲分析

一个悬臂P-GPLs-FGP板的尺寸为a×b×h=400 mm×400 mm×5 mm,中间层的基体材料为黄铜,上、下压电层为PZT-G1195N,厚度hp=0.1 mm。石墨烯纳米片的尺寸和质量参数与2.1.1节相同,且e0=0.2。表3给出了不同孔隙和石墨烯分布形式下,板在q0=-100 N/m2均布机械载荷和电载荷作用下的中心线末端挠度。对比可知,同样是基于IGA框架,本文采用简化一阶剪切变形理论的结果与Nguyen等采用高阶剪切变形理论的结果较为吻合。

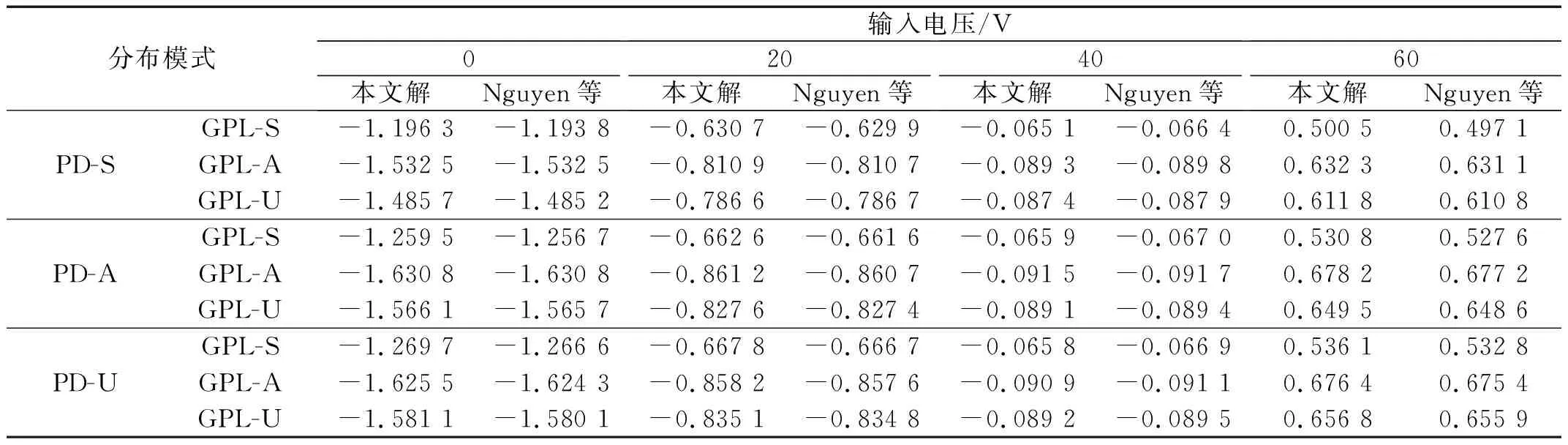
表3 机电载荷作用下悬臂P-GPLs-FGP板的末端挠度Tab.3 Tip deflection of the cantilevered P-GPLs-FGP plate subjected to the electro-mechanical loads 单位:10-4m

2.2 自由振动分析

一个P-GPLs-FGP板的尺寸为:a=b=400 mm,中心层是厚度为hc的铝基GPLs-FGP板,上、下层是厚度为0.1 mm的PZT-G1195N。表4为WGPL=1.0 %,e0=0.2时,孔隙分布形式、石墨烯分布方式、基体的宽厚比和电学条件对四边简支板的固有频率的影响。电学边界条件分为短路和开路两种,当电场强度为零而电位移不为零时,电学边界条件为短路;当电位移为零而电场强度不为零时,电学边界条件为开路。结果表明:①对于每一种孔隙分布,石墨烯为非均匀对称分布(GPL-S)时板的固有频率的最大,因此GPL-S型石墨烯分布方式对板的增强效果最好;②对于每一种石墨烯分布,板在孔隙非均匀对称分布(PD-S)时的固有频率最高;③开路边界状态下板的频率略高于短路状态;④随着宽厚比的增大,板的固有频率逐渐减小。表5给出了hc=20 mm、PD-S和GPL-S分布时孔隙系数和石墨烯质量分数对四边简支和四边固支板前六阶固有频率的影响。可以看出,石墨烯质量分数的增大会引起板固有频率的增大,而孔隙系数的增大使得板的固有频率先减小后增大,且CCCC板的固有频率高于SSSS板的固有频率。图4为四边简支板的前六阶固有振型。为进一步验证石墨烯质量分数WGPL与孔隙数e0对板固有频率的影响,图5为e0=0和e0=0.2时,石墨烯质量分数对不同孔隙和石墨烯分布形式下板固有频率的影响。由图5可知:①板内部不含孔隙(e0=0)和含孔隙(e0=0.2)时,固有频率与石墨烯质量分数都近似呈线性关系,且固有频率随石墨烯质量分数增大而增大;②对于每一种孔隙分布,GPL-S型石墨烯分布方式对固有频率的增强效果最好。图6为WGPL=0 %和WGPL=1.0 %时,孔隙系数对不同孔隙和石墨烯分布形式下板的固有频率的影响。可以看出:①PD-A和PD-U型孔隙分布时板的固有频率随孔隙系数增大而减小;②PD-S孔隙分布时固有频率先随孔隙系数的增大小幅度地减小,但当孔隙系数增大至一定程度时,固有频率随孔隙系数增大而增大。造成这种现象的原因是,孔隙系数的增大会同时减小基体的刚度和质量,当孔隙系数增大到一定程度时,质量的减小速率大于刚度的减小速率,使得固有频率呈现增大的趋势,该结论也与Gao等的结论一致。

表4 e0=0.2,WGPL=1.0%时P-GPLs-FGP板的固有频率Tab.4 Natural frequency of the P-GPLs-FGP plate with e0= 0.2,WGPL=1.0% 单位:Hz

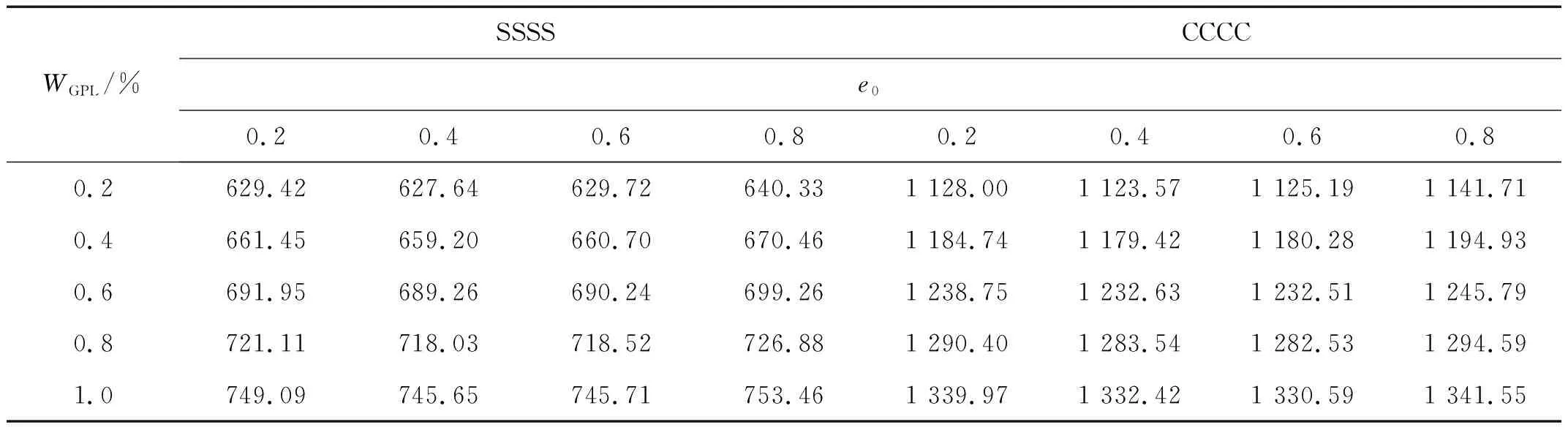
表5 石墨烯质量分数和孔隙系数对P-GPLs-FGP板固有频率的影响Tab.5 Effects of GPLs weight fraction and porosity coefficients on natural frequencies of the P-GPLs-FGP plate 单位:Hz

图4 四边简支板的前六阶固有振型Fig.4 First six mode shapes of the SSSS plate

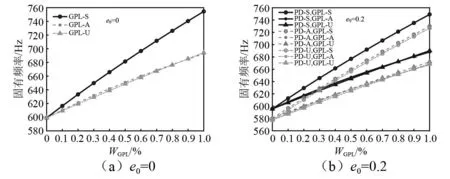
图5 石墨烯质量分数对固有频率的影响Fig.5 Effect of GPLs weight fraction on the natural frequency

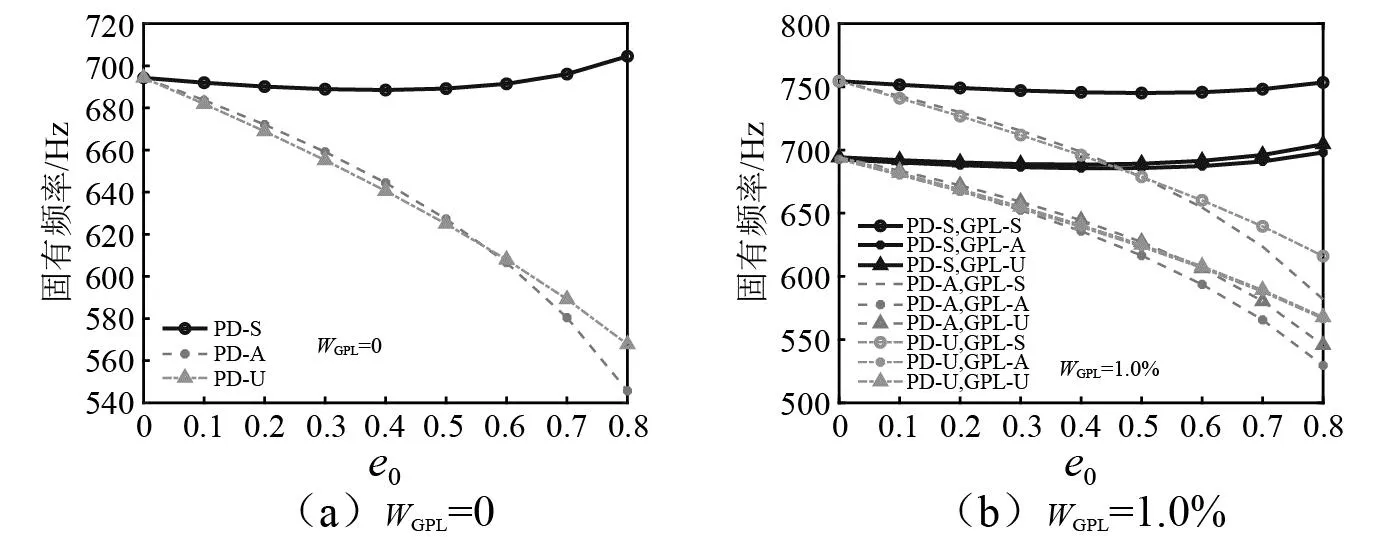
图6 孔隙系数对固有频率的影响Fig.6 Effect of porosity coefficient on the natural frequency

综合图5和图6可知,孔隙和石墨烯均为非均匀对称分布(PD-S,GPL-S)时板的固有频率最大。这是因为对称分布时基体的上下面石墨烯密度大,孔隙体积小,使得石墨烯和基体充分结合,发挥其高刚度特性,增强板的承载能力。

图7为不同边界条件下,不含孔隙系数(e0=0)和石墨烯(WGPL=0)时(纯铝板)与含孔隙(e0=0.2)和石墨烯(WGPL=1.0 %)时在不同的分布形式下板固有频率的变化趋势。同样可以看出,不同边界条件下,孔隙和石墨烯为非均匀对称分布形式时板的固有频率最大。而且因为固支条件对结构的约束性更强,因此CCCC板的固有频率>SCSC板的固有频率>SSSS板的固有频率>CFFF板的固有频率。

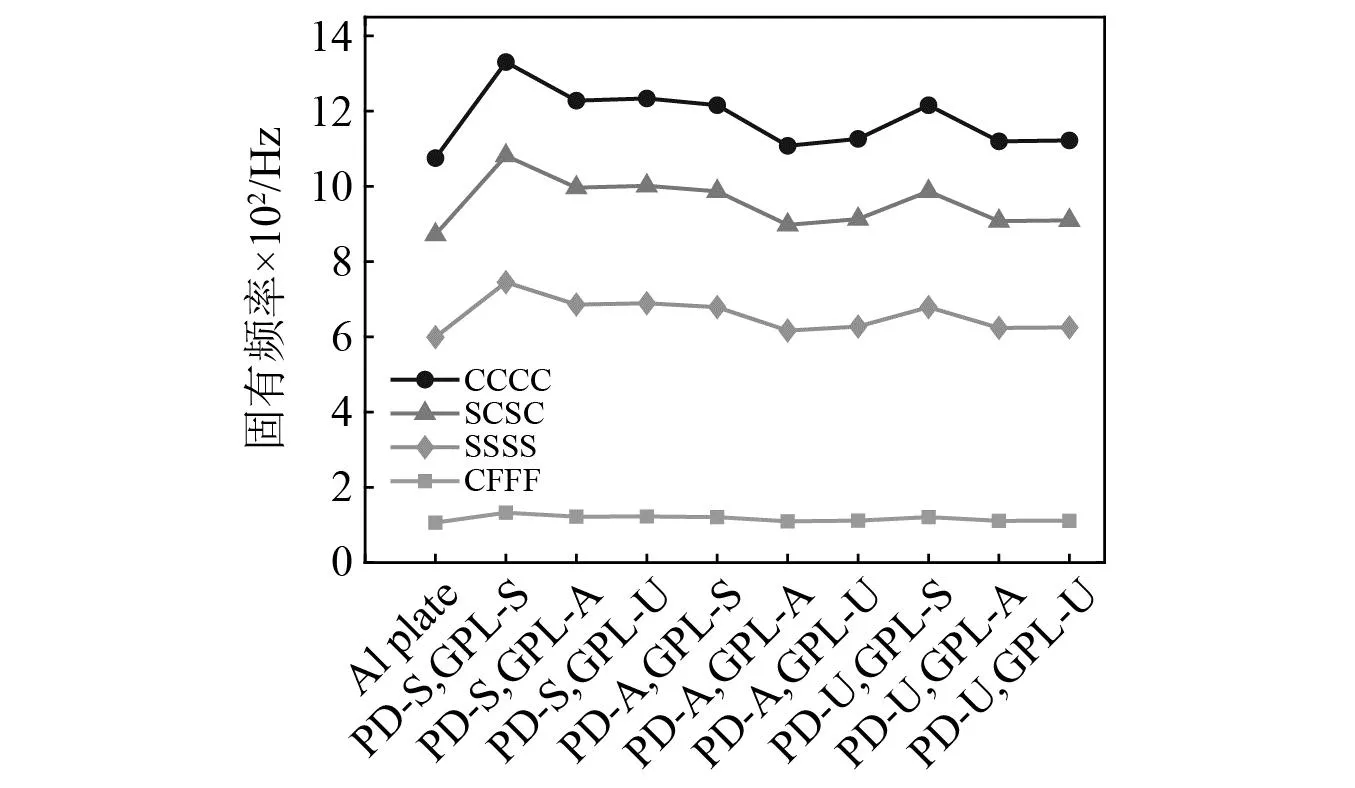
图7 不同机械边界条件下P-GPLs-FGP板的固有频率Fig.7 Natural Frequencies of P-GPLs-FGP plate with different mechanical boundary conditions

2.3 静态弯曲分析

假设WGPL=1.0 %,e0=0.5,图8所示为不同孔隙和石墨分布形式下悬臂板和四边简支板在机械载荷q0=-100 N/m2和电载荷UE=5 V下的挠度。可以看出:①不同载荷下PD-S和GPL-S型分布组合时板的挠度最小;②对于每一种孔隙分布,石墨烯GPL-S型分布对板的刚度增强效果最好,GPL-U型其次,GPL-A型最差;③对于每一种石墨烯分布,孔隙PD-S型分布时刚度最大,其次分别为PD-U和PD-A型分布。

图8 不同载荷下孔隙和石墨分布形式对挠度的影响Fig.8 Effect of distribution types of porosity and GPLs on the deflection under different loads

为进一步研究孔隙系数和石墨烯质量分数对板静态弯曲响应的影响,图9和图10分别为机-电载荷下板的挠度随孔隙系数和石墨烯质量分数的变化趋势。可以看出:①孔隙的增大导致板的刚度减小,因此挠度增大;②通过在基体中添加微量的石墨烯,能有效地增强板的刚度,石墨烯质量分数越大,板的刚度越大,挠度越小;③随孔隙系数和石墨烯质量分数增大,PD-S型和GPL-S型分布形式组合时板的刚度仍然最大,挠度最小。

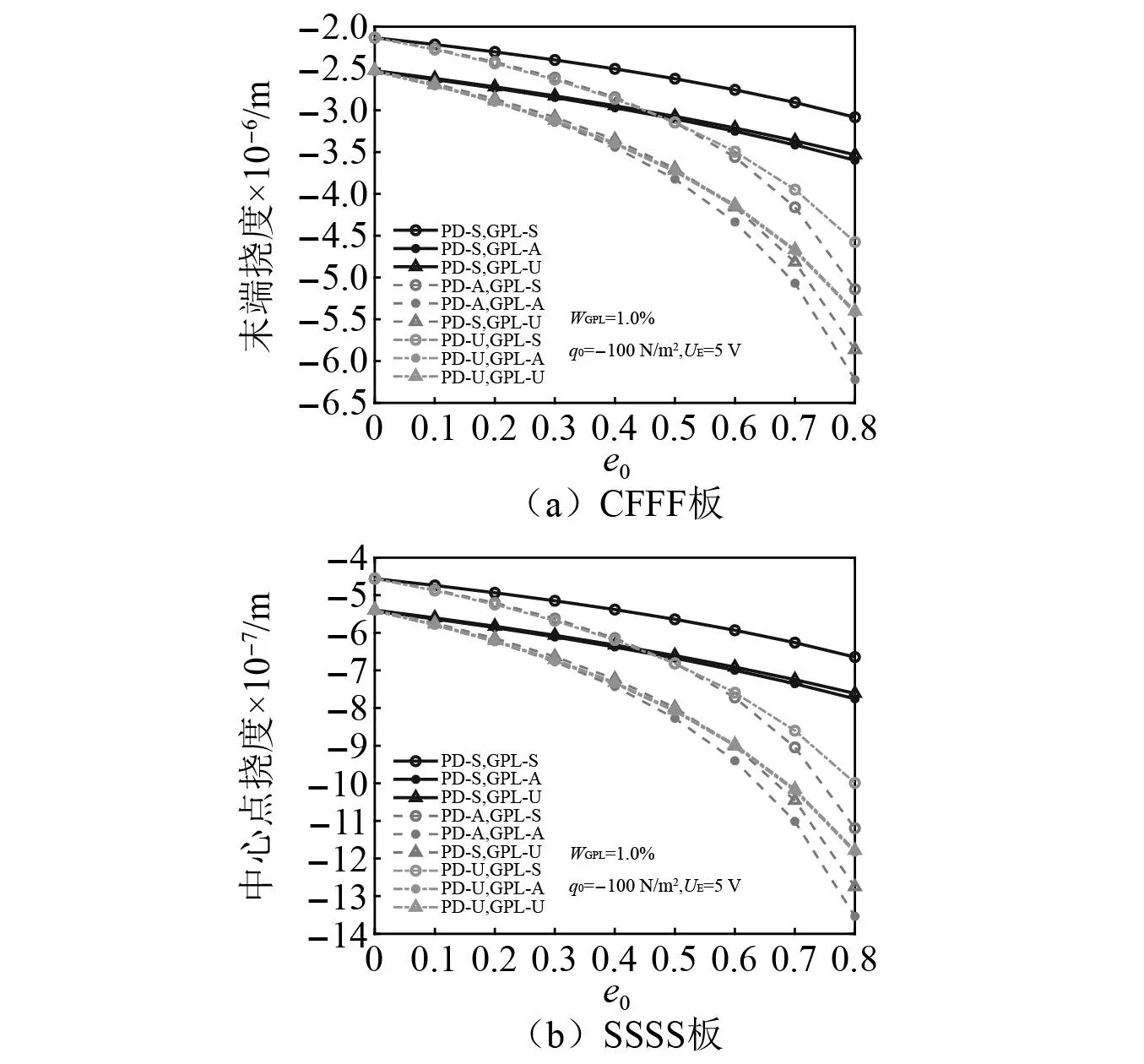
图9 孔隙系数对P-GPL-FGP板挠度的影响Fig.9 Effect of porosity coefficient on the deflection of P-GPL-FGP plates

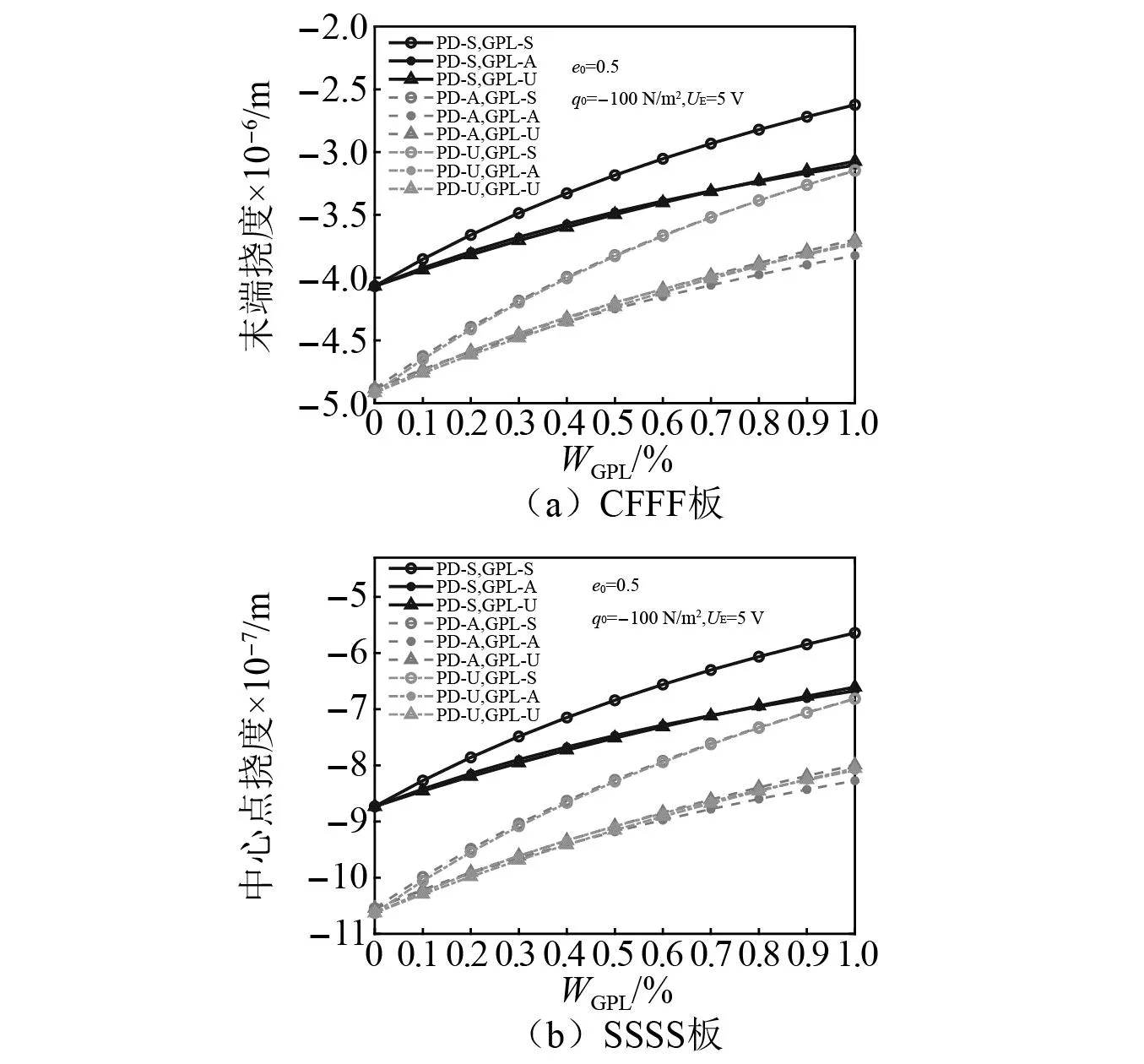
图10 石墨烯质量分数对P-GPL-FGP板挠度的影响Fig.10 Effect of GPLs weight fraction on the deflection of P-GPL-FGP plates

图11为板的宽厚比对P-GPLs-FGP板静态弯曲响应的影响。由图可知,宽厚比对板的挠度有明显影响,随宽厚比增大,板的整体刚度减小,挠度增大,宽厚比小于30时板的变形量较小且相对稳定。

图11 宽厚比对P-GPL-FGP板挠度的影响Fig.11 Effect of width-to-thickness ratio on the deflection of P-GPL-FGP plates

3 结 论

本文基于简化一阶剪切变形理论和等几何方法建立了P-GPLs-FGP板的等几何数值分析模型,研究了孔隙分布形式、石墨烯分布方式、孔隙系数、石墨烯质量分数以及结构的宽厚比对板的自由振动和静态弯曲响应的影响,得出下列结论:

(1) 与已有等几何分析框架下的高阶剪切变形理论结果相比,该模型能够较准确地反映板的自由振动和静态弯曲响应。

(2) PD-A和PD-U分布时固有频率随孔隙增大而减小,PD-S分布时板的固有频率先随孔隙系数的增大小幅度地减小,但当孔隙系数增大至一定程度时,固有频率随孔隙系数增大而增大;石墨烯质量分数增大,板的固有频率增大。

(3) 孔隙系数增大,板的刚度减小,挠度增大;石墨烯质量分数增大,板的刚度增大,挠度减小。

(4) 石墨烯GPL-S型分布对板刚度的增强效果最好;孔隙PD-S型分布时板的刚度最大。因此,PD-S型和GPL-S型分布形式组合时板的刚度最大。