传递矩阵法在计算输流管路高频振动时的稳定性改进

曹银行, 柳贡民, 胡 志

(1. 哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001; 2. 哈尔滨工程大学 烟台研究生院,山东 烟台 264006)

在管路系统的流固耦合振动特性研究中,建立合适的数学模型和配套的计算方法是关键[1]。目前为止,常采用的计算模型包括基于一维梁及流体平面波理论的4方程模型[2-4]、8方程模型[5-6]和14方程模型[7-9]等。计算方法则分为时域方法和频域方法[10]。其中频域传递矩阵法(transfer matrix method, TMM)只需要将每个管路元件作为一个整体单独处理,不需要根据其结构尺寸进行空间离散,涉及的自由度少[11]。此外,TMM还具有易于编程,计算效率高等优点。

多篇文献提及,基于14方程模型和TMM计算大跨度管路高频振动响应时存在数值不稳定的现象,认为这严重限制了TMM的使用,有必要加以改进[12-13]。De Jong的研究表明,直管14方程模型中,轴向、横向和扭转运动可以相互解耦,而计算失稳现象只存在于横向振动的计算中。有鉴于此,本文的研究只考虑管路在y-z平面内的横向运动,不考虑其在x-z平面内的横向运动以及轴向和扭转运动。

Riccati传递矩阵法(riccati transfer matrix method,RTMM)将传统TMM中状态向量的传递转变为Riccati矩阵的传递,将管路振动特性的求解从一个两点边值问题转化为一点初值问题,在降低计算矩阵维度的同时有效提高了数值解的稳定性[14]。但是RTMM可能会引入奇异频率和奇异截面两个病态问题[15];同时RTMM必须根据边界条件将状态向量分为已知元素和数目相等的互补元素以确保Riccati矩阵是一个方阵;最后RTMM在计算过程中需要先求得Riccati矩阵的初始值。RTMM很难处理复杂边界条件下的振动计算,如弹性支撑和多激励边界、柔性边界等。

全局传递矩阵法(global transfer matrix method, GTMM)是另一种常用的改善TMM计算稳定性的方法。为避免过大的“特征长度”,GTMM将大跨度的管路划分为若干个子单元,而全局矩阵由各子单元的平行处理得到。由于划分的子单元数目决定了全局矩阵的维度,并进而影响到GTMM的计算速度,De Jong提出了子单元划分的“条件数”标准。但其建立的传递矩阵和条件数推导过程在考虑流动和压力带来的离心力和科氏力的影响后会将变得非常困难。

综上所述,本文将重点讨论TMM的改进方法,以使其能够基于更先进的数学模型,稳定、快速地计算大跨度输流管路系统的横向振动。本文提出了基于无量纲化计算结果得到的子单元划分准则的GTMM、混合能传递矩阵法(hybrid energy transfer matrix method,HETMM)和结合变精度算法的传递矩阵法(hybrid energy transfer matrix method,VPA-TMM)等三种改进方法并指明了其各自的优缺点。

1 De Jong的子单元划分标准

De Jong采用的输流管路面内横向振动的频域方程与Timoshenko梁的弯曲方程一致

(1)

(2)

(3)

(4)

符号和下标的含义如表1所示。

表1 符号和下标的含义Tab.1 Meaning of symbols and subscripts

式(1)～式(4)的特征方程为

(5)

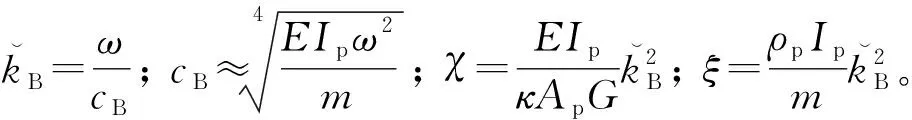
在低频段(ξ≪1;χ≪1),式(5)的特征值满足

(6)

式中,kB和kN分别为传播波和近场波。

直管传递矩阵的条件数与exp(kNL)处于同一数量级。在PC中,计算值分辨率为10-16,因此当kNL≥ln(1013)时,舍入误差变得很重要(大于0.1%)并使计算结果出现不稳定的现象。在计算频率上限不变的情况下,De Jong提出利用划分子单元的方法降低单段管路的“特征长度”,对于这些子单元,其条件数都要小于一个预定的值。即

划分后的子单元应利用GTMM平行处理。

2 无量纲模型得到的子单元划分标准和GTMM

本章采用较简单的拉普拉斯变换法获取传递矩阵,并从计算结果的角度建立新的子单元划分准则,而De Jong则从数值不稳定的原因出发,且实践证明是更保守的。最后本节还将给出GTMM的具体实现措施。式(7)～式(10)如下

(7)

(8)

(9)

(10)

2.1 基于拉普拉斯变换的传递矩阵推导

包含式(7)～式(10)中四个独立变量的时域状态向量可表示为

之后式(7)～式(10)可以写为矩阵方程的形式

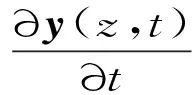
(11)

式中,B,C为4×4的系数矩阵。令y(z,0)=04×1,式(11)可以通过拉普拉斯变换ζ转换到频域进行求解

(12)

用U和V分别表示A-1B的特征值矩阵和特征向量矩阵,并令v(z,s)=V-1Φ(z,s),式(12)可以简化为

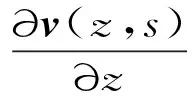
(13)

式(13)是一个一阶微分方程,其解可以由式(14)直接给出。

v(z,s)=E(z,s)v0(s)

(14)

其中,

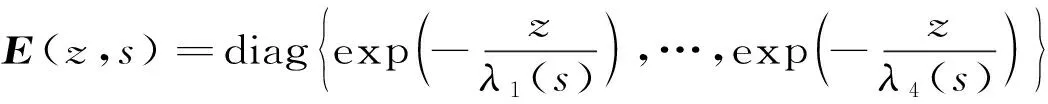
将v(z,s)=V-1Φ(z,s)代入式(14)可得

Φ(z,s)=VE(z,s)v0(s)

(15)

令z=0,则E(0,s)=I4×4,再代入式(15)可以得到v0(s)=V-1Φ(0,s)。进而式(14)可以转化为

Φ(0,s)=VE-1(z,s)V-1Φ(z,s)

(16)

式中,VE-1(z,s)V-1=T为横向振动的场传递矩阵。

基于拉普拉斯变换的传递矩阵推导避免了建立特征方程时的“消元”过程,因此更加简单,不易出错。同时它只需要处理一阶微分方程式(13)。

2.2 TMM的高频失稳现象

输流管路横向振动的TMM计算公式为

(17)

式中:Ds,De为具有相似形式的始末端边界条件矩阵;Fs,Fe分别为作用于管道两端的频域激励。

式(17)可以简化为

DoveΦove=Fove

(18)

式中,Dove,Φove,Fove分别为整体传递矩阵、整体状态向量和整体激励向量。通过求解式(18)可以得到Φove,其第一部分是管路始端的状态向量;任意一点的状态向量都进而可以通过式(16)得到。

如图1所示的Dundee管道为例,其参数如表2所示。 管路两端自由,内部流体被无质量的堵头封闭,所以流速等于0,初始压力也为0。

图1 Dundee管Fig.1 Dundee pipe

表2 Dundee管的材料与流体特性参数Tab.2 Material and fluid properties of dundee pipe

在B点施加一个单位力或力矩的脉冲激励,计算得到的B点横向振动和转动响应如图2和图3所示。TMM计算结果在高频段出现了明显的计算失稳现象,这是因为传递矩阵VE-1(z,s)V-1=T中也有类似于exp(kNL)的元素,即exp[z/λ(s)],同时也包含那些数值很小的元素,所以计算结果数值不稳定的原因和通过子单元划分构建全局矩阵的解决方法可以和De Jong的研究相同。

图2 B点的横向振动速度响应计算结果Fig.2 Calculated results of the transverse vibration velocity response at point B

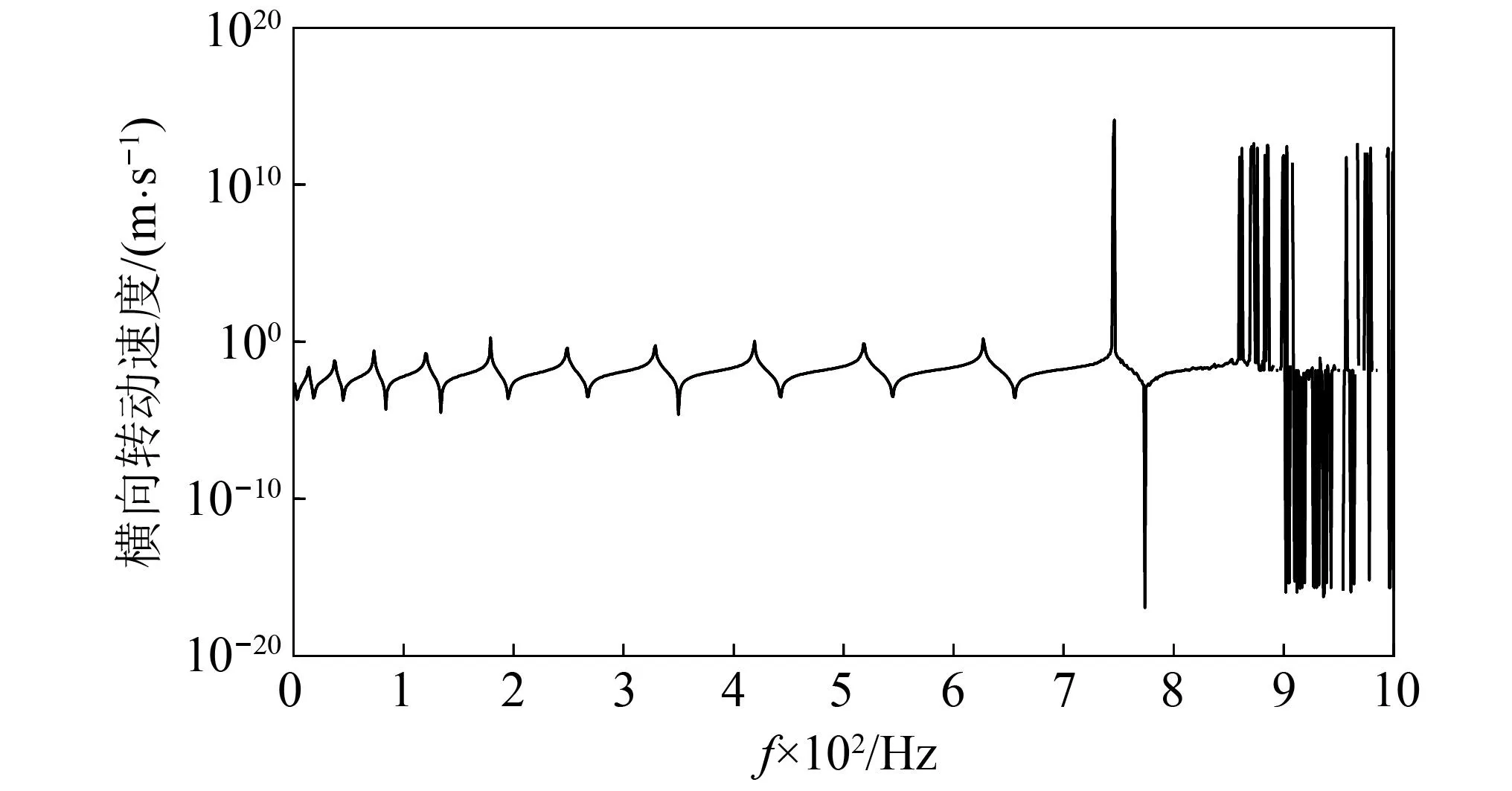
图3 B点的横向转动速度响应计算结果Fig.3 Calculated lateral torsional velocity response at point B

2.3 根据无量纲化计算结果得到的子单元划分标准

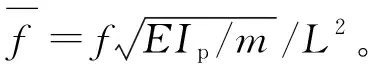
其中,μ为管路材料泊松比。用上述无量纲参数替换式(7)～式(10)中的相应项可得到无量纲的横向振动4方程模型

(19)

(20)

(21)

(22)

基于无量纲4方程模型的传递矩阵推导和输流管路横向振动计算与2.1节和2.2节相同,这里不做赘述。

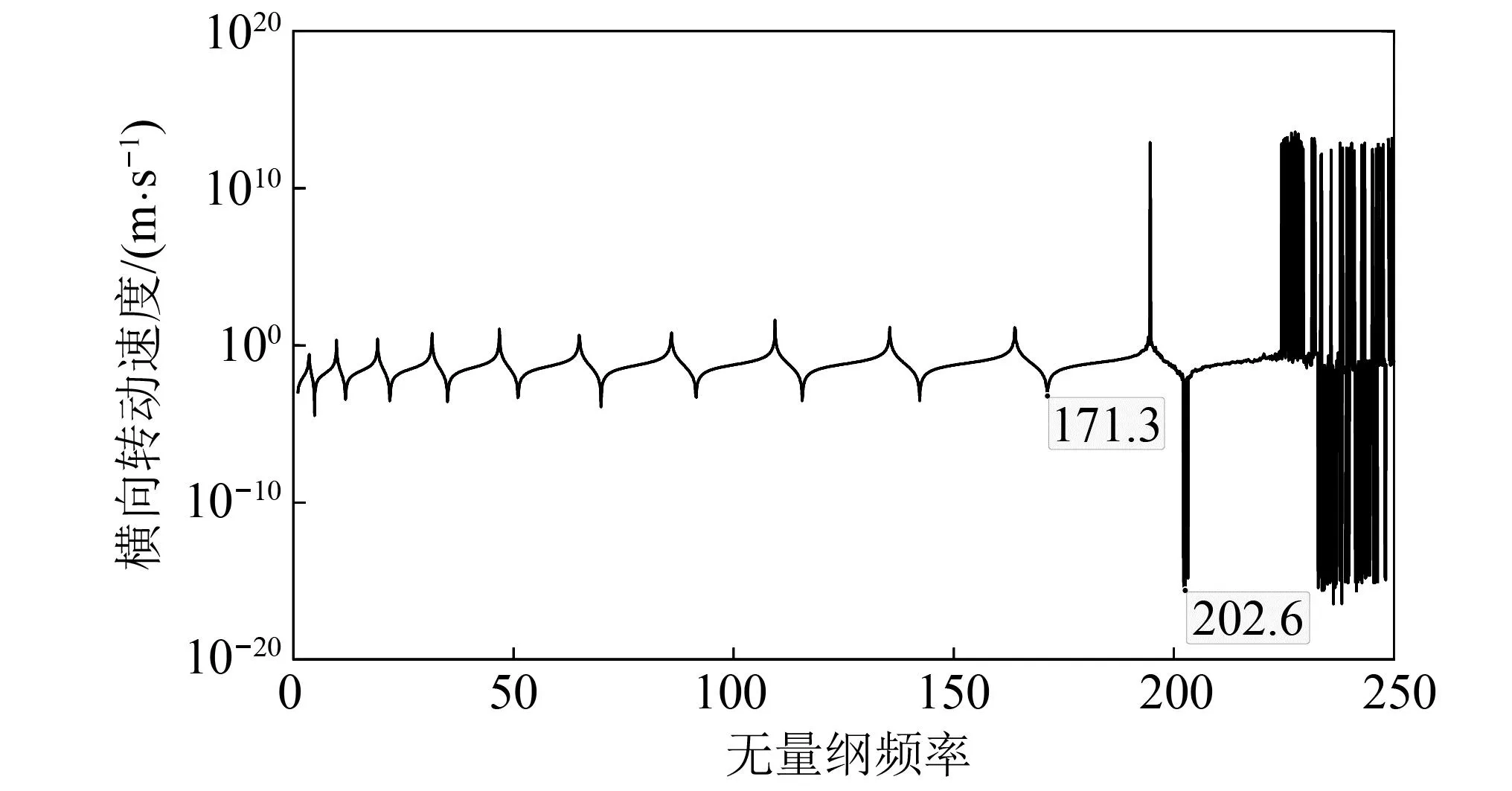
图4 B点的横向转动速度响应计算结果Fig.4 Calculated lateral torsional velocity response at point B

(23)

2.4 新的子单元划分标准的验证和GTMM的实现

图5 7.2 m管路分析模型Fig.5 7.2 m pipe analysis model

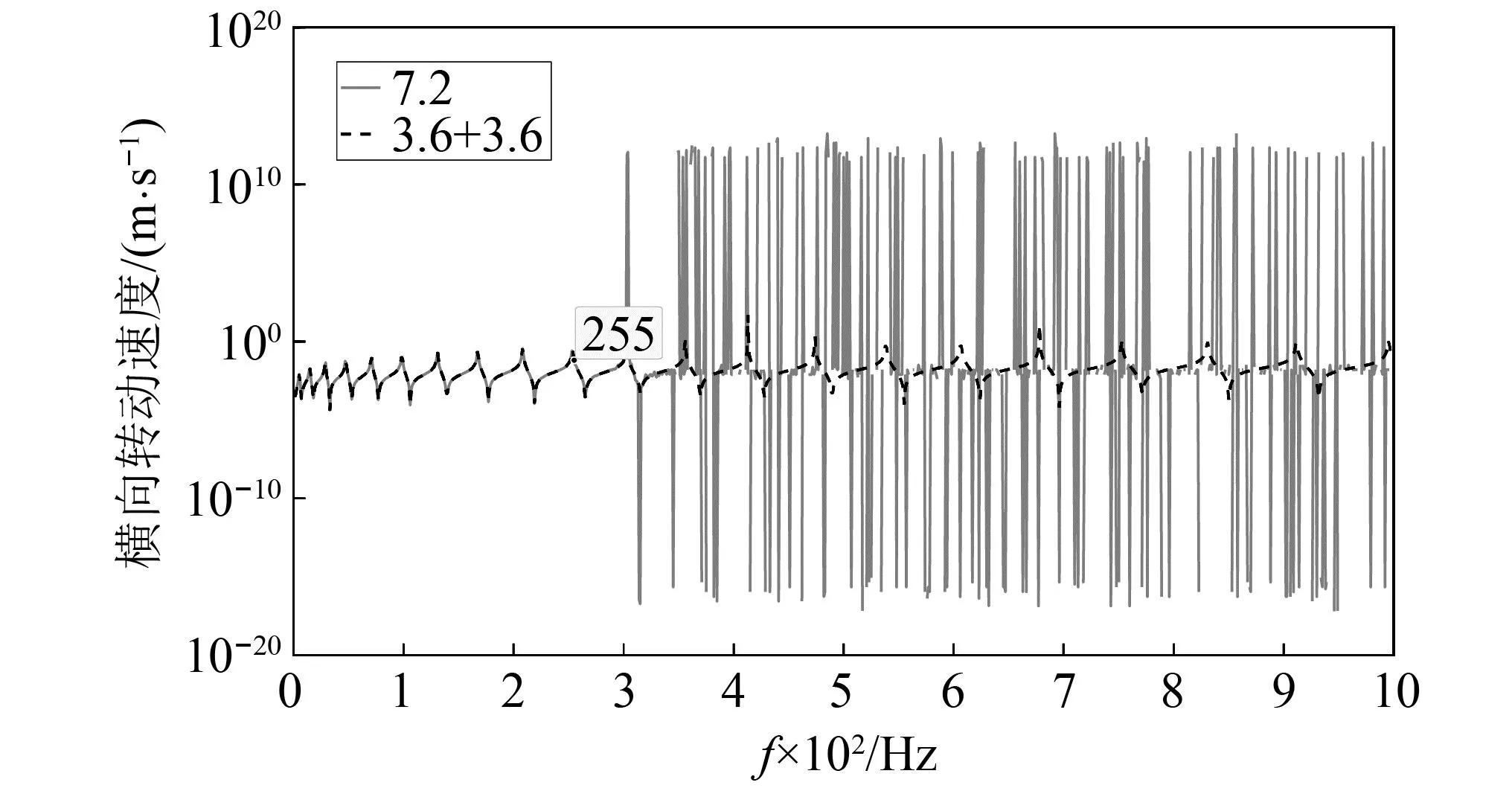
图6 E点的横向转动速度响应计算结果Fig.6 Calculated lateral torsional velocity response at point E

根据式(23)可知,只有最大的管道子单元长度取小于等于3.6 m的值时才能获得1～1 000 Hz内稳定的计算结果;7.2 m长的管道应先划分为两个子单元CE=DE=3.6 m再进行GTMM计算,全局矩阵的维度为12×12,即

直接利用TMM计算式(17)与二单元GTMM计算结果的对比见图6。如图6所示,基于子单元划分的GTMM明显保证了TMM在高频下的计算稳定性,同时也说明依据式(23)来划分大跨度的管路是有效可行的。

图5的算例中,流体速度和压力均等于0,式(1)～式(4)和式(7)～式(10)可视为等价的,但根据De Jong的研究,1～1 000 Hz内TMM计算稳定时管路子单元的最大划分长度为3.3 m,所以图5中的计算模型应划分为3个子单元并采用16×16的全局矩阵,这显然是更为保守和复杂的,计算所需时间也会因子单元数目的增加而增加。

3 管路振动计算的混合能传递矩阵法

高强等人建立了一种求解层状介质中波传播问题的稳定方法,并将其命名为混合能矩阵法[17-18]。本节首次在流体管路系统横向振动计算的TMM中引入混合能矩阵法的思想,给出了程式化的计算过程,解决了TMM高频响应计算失稳的问题。首先仍然利用拉普拉斯变换的方法来获取传递矩阵,但是这里取Φ′(z,s)=T′Φ′(0,s)。即

(24)

引入两个混合能向量[qi,pi-1]T,[qi-1,pi]T,它们分别结合了管道子单元一端的速度变量及其另一端的力(力矩)变量,并且根据式(24)可得

(25)

式中,G,Q可分别看作动柔度矩阵和动刚度矩阵,根据式(25)还可以得到

(26)

结合式(25)和式(26)则可以得到

(27)

其中,

Mi-1,i+1=Mi,i+1(I2×2+Gi-1,iQi,i+1)-1Mi-1,i

(28a)

(28b)

(28c)

Ni-1,i+1=Ni-1,i(I2×2+Qi,i+1Gi-1,i)-1Ni,i+1

(28d)

重复使用式(25)～式(28),可以得到当大跨度的管路被划分为n个子单元时,始末端混合能向量之间的关系满足

(29)

对于图1和图5中的计算模型,A(D)点和B(E)点的管路自由边界条件满足

将边界条件与式(29)结合可以得到

(30)

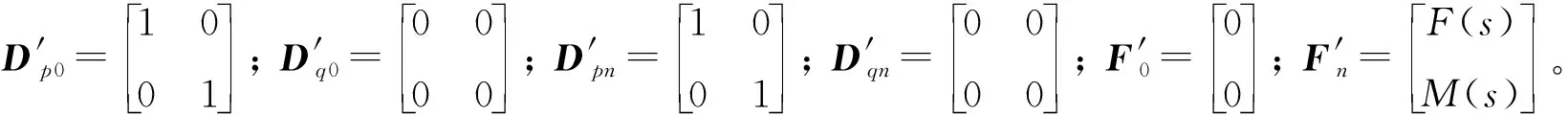
将Dundee管划分为2～4个子单元时HETMM的横向振动速度响应计算结果见图7。同时如图8所示,在最短的计算时间内,HETMM利用少量的子单元就可以得到在800 Hz之前与GTMM,RTMM和TMM一致,且在1～1 000 Hz内稳定的计算结果。

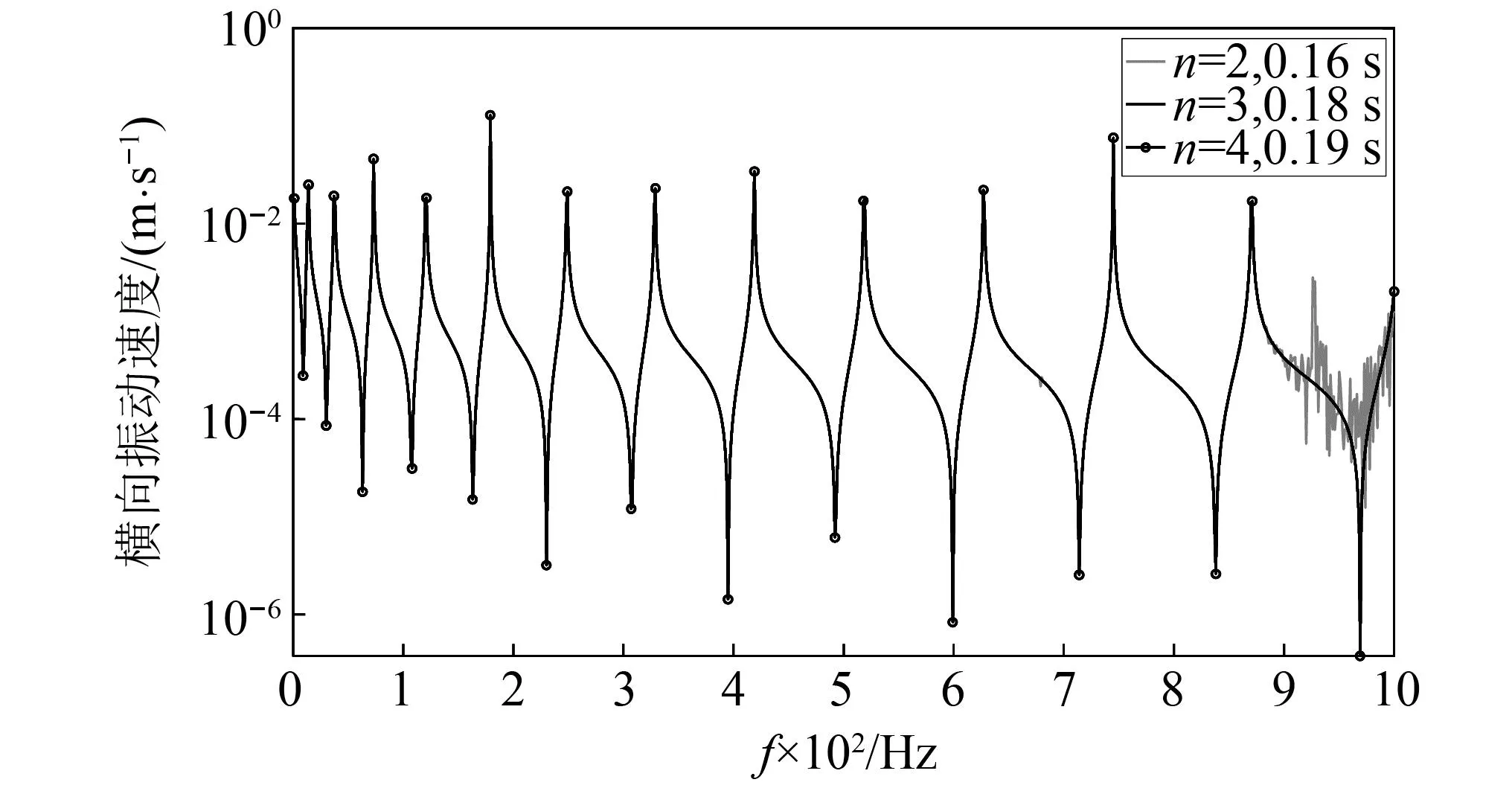
图7 B点的横向振动速度响应的HETMM计算结果Fig.7 HETMM calculation of the transverse vibration velocity response at point B

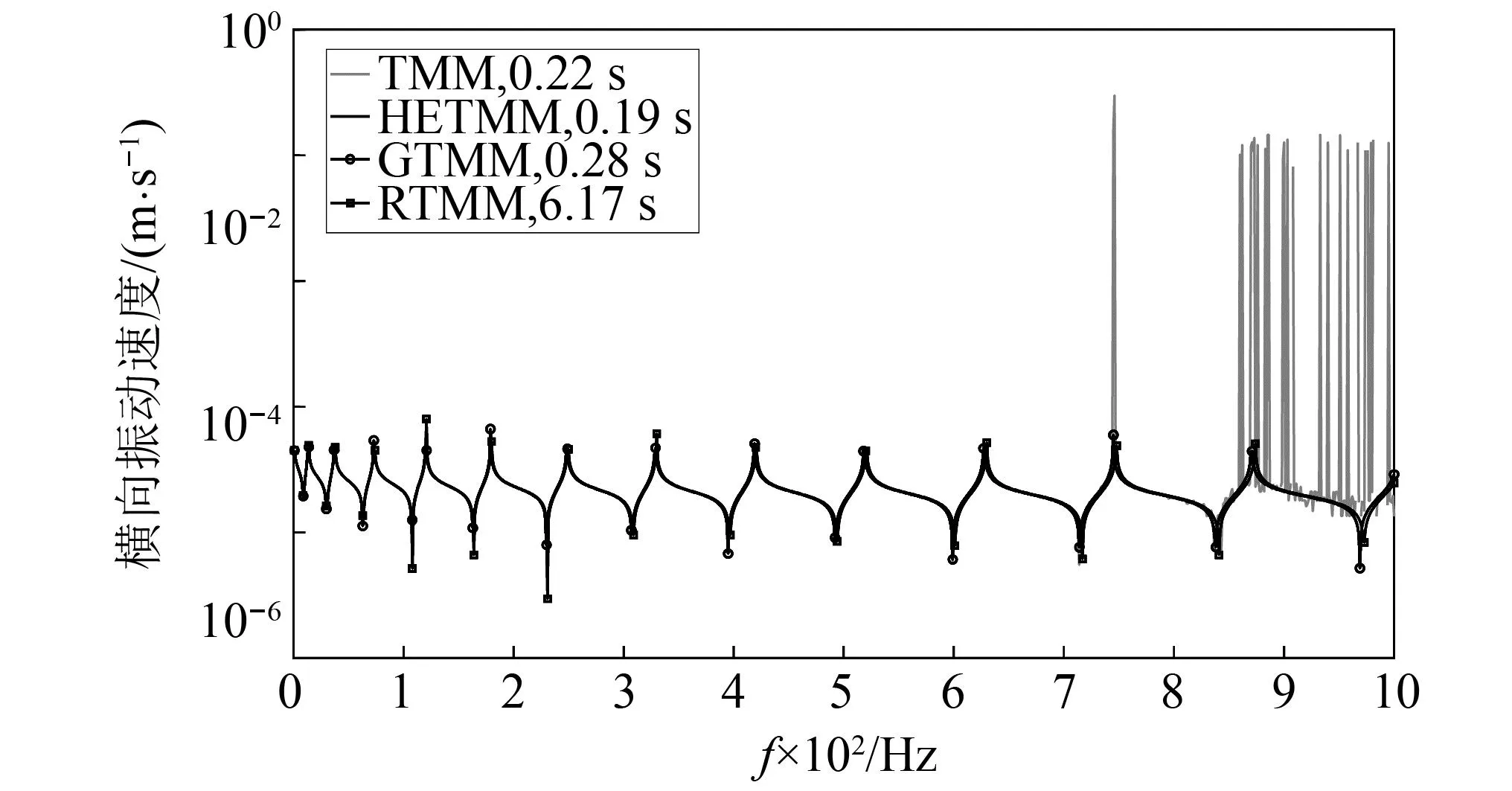
图8 B点的横向振动速度响应计算结果Fig.8 Calculation results of the transverse vibration velocity response at point B

4 结合高精度算法的传递矩阵法

De Jong的研究指出了TMM在高频段计算不稳定的根本原因是由于计算机使用大约16位小数来表示一个实数而引起的舍入误差问题。因此,TMM计算结果出现不稳定的现象是一个数学问题,而不是过大的“特征长度”这一物理问题。但是,无论De Jong本人还是后来的研究者都对长跨度的管道进行了一定程度的子单元划分,都可以看作是从物理角度而非从根本上来解决TMM计算数值不稳定的问题。

Symbolic Math Toolbox提供了sym和vpa两种方案,通过使用符号化或可变精度的数字来解决计算机的舍入误差问题。两种计算方案与计算机默认的双精度(16位小数,即前文所述PC的计算值分辨率10-16)方案对于sin(π)的计算结果与误差分析如表3所示。

表3 不同方案下对 sin(π) 的计算Tab.3 The calculation of sin(π) under different schemes

通过设置合理的字节数(这里选取为32字节),并以vpa格式输入TMM计算程序中的相关参数,不需要对2.1节和2.2节中传递矩阵和TMM整体方程的推导和计算过程进行任何修改就可以得到稳定的结果,如图9所示。

与GTMM和HETMM相比,最高可设置1 024位字节数的VPA-TMM可视为一种能够一劳永逸地解决TMM长跨度高频计算数值不稳定问题的改进方法,但其所需内存和计算时间也会大大增加。对于E点的振动响应计算,GTMM需要0.286 379 s,HETMM需要0.181 202 s。当利用vpa函数设置字节数为16～27时,VPA-TMM无法得到1～1 000 Hz内稳定的振动响应计算结果,而当设置28～35位字节时的计算时间如表4所示。

5 GTMM,HETMM与VPA-TMM的比较

GTMM,HETMM与VPA-TMM这三种方法都以传统TMM为基础,故而都能以与传统TMM相同或相似的方式方便统一地处理各种边界支撑和激励条件。关于它们的其它优缺点的讨论如下。

(1) 全局传递矩阵法GTMM

传统的TMM经过多年的发展已经形成了较为完善的计算和理论体系,各类常见的管路系统元件,如直管、弯管、管路支撑、分支管等的传递矩阵模型和各类常见的边界条件模型及其建立过程都可见于各种文献,并进而可以轻而易举地应用于GTMM。但随着管路系统跨度或元件数量的增加,全局矩阵的形式要不断更新。即使可以通过更好的子单元划分标准,矩阵维度和计算时长的增加也是不可避免的。

(2) 混合能量传递矩阵法HTEMM

HETMM计算矩阵的维度小,计算时间最短,管路系统子单元数量增加时,计算矩阵的形式也能保持不变,使得计算程序也几乎无变化,可以无成本地进行试算以确定合适的子单元划分数目。但作为本文新引进的一种管路系统动力学特性分析方法,HETMM的发展还不如传统的TMM成熟。HETMM需要对现有的传递矩阵和边界条件模型进行进一步的改造,这是它的缺点,同时也似乎是它的优点。

(3) 变精度算法与传递矩阵法相结合的方法VPA-TMM

VPA-TMM可以从根本上解决TMM高频段计算结果不稳定的问题,而且不需要改变传递矩阵的推导过程、形式和整体计算矩阵,但计算时间和成本明显增加。虽然可以通过设置合理的字节数在一定程度上减少计算时间,但幅度也非常有限。VPA-TMM不适合大型管路系统动力学特性计算或管路系统优化设计这种需要大量样本计算的情况。

关于3种方法的比较如表5所示。

表5 3种TMM改进方法的比较Tab.5 Comparison of 3 TMM improvement methods

6 结 论

本文提出了三种方法来解决TMM高频计算结果不稳定的问题,即基于无量纲模型计算结果得到的子单元划分标准的GTMM,HETMM和VPA-TMM。与RTMM相比,这三种方法都能程式化地处理各种边界支撑和激励条件,并且都是基于更全面地考虑了流体速度和压力影响的4方程模型和更简单的拉普拉斯变换方法来获取的传递矩阵。

在这三种方法中,HETMM系首次从层状介质中的波传播计算扩展到管路系统的振动分析领域,可以直接以较为成熟的TMM为基础。HETMM计算矩阵的维度和形式不随子单元数目的增加而改变,计算时间又是最短的。可以认为HETMM是这三种方法中最好的一种。