混流式喷水推进泵空化流动及其诱导振动特性的试验研究

龚 波, 张正川, 尹俊连, 许 锐, 李 宁, 王德忠

(1. 上海交通大学 机械与动力工程学院,上海 200240; 2. 中国船舶工业集团公司第七〇八研究所 喷水推进技术重点实验室,上海 200111)

空化流动是一种液体特有的复杂的流体动力学现象,包含了湍流、多相流、可压缩等一系列非定常流动特性[1]。空化现象对水力机械主要有三点影响:导致水力机械性能下降、增加水力机械振动噪声、破坏过流表面。同时空化还是排灌、水电、航空航天、舰艇等领域面临的关键性的技术难题[2-3]。

空化是一个极其复杂的科学问题,许多学者对其进行了研究。Parsons早在1896年就建立了第一个空化水洞,进行了螺旋桨空化现象的研究[4]。Brennen[5]在空化发展过程中按照空泡形态将空化程度划分为:初生空化、片状空化、云状空化和超空化。Zhang等[6]对具有尖锐前缘的超空化水翼进行了试验研究发现,空化尾流中出现两旋转方向相反的旋涡,上涡沿顺时针旋转,下涡为逆时针旋转。随着空化数的降低,空化涡街现象趋于明显;随着空化数的进一步降低,出现明显的云状空化附着于水翼的吸力面,并形成周期性脱落的空化云。Guennoun等[7]则采用了微型压力传感器和高速摄像机同步测量技术揭示了游离型空泡的形成机理和周期性水动力特性。刘韵晴等[8]对绕弹性水翼空化流激振动特性进行了试验研究,结果表明水翼在云状空化阶段下振动最为剧烈,大尺度空泡的周期性脱落导致结构的振动速度呈现周期性变化;云状空化阶段,在较大空化数下因回射流机制导致空泡的非定常脱落,在较小空化数下因水汽激波机制导致空泡的非定常脱落,不同脱落机制下结构振动特性存在显著差异。

推进装置的效率高低决定着船舰的机动性,推进装置的振动一方面会影响船舰的安全性;另外一方面还会导致船舰向外辐射噪声,向外辐射的噪声则会影响船舰的隐身性。喷水推进是高性能舰船常用的推进方式,喷水推进泵是喷水推进装置的核心部件。喷水推进泵是一个复杂的流固耦合振动系统[9-10]。非定常空化也是泵内的一种十分不利的流动现象,会导致泵的做功能力下降,效率的降低,并产生非定常激励,诱导泵体产生振动和噪声[11]。喷水推进泵发生非定常空化现象时对整个船舰极为不利。

受到船舰的安装空间限制,喷水推进泵的泵型通常采用轴流泵或者导叶式混流泵。已经有不少国内外学者进行了喷水推进泵非定常空化流动相关研究,且主要以试验的方式来研究轴流泵内的空化流动现象。Dreyer等[13]的PIV试验研究结果表明由于旋转叶片的压力面对流体做功,导致压力面的压力远大于吸力面;在压力的推动下流体会由压力面经叶顶间隙泄露至吸力面;在剪切力的作用下叶顶泄漏流在叶片吸力面侧与主流卷吸形成叶顶泄漏涡。Wu等[14-15]的试验结果表明间隙涡和泄露涡结构十分复杂,叶顶剪切层和吸力面的低压区会诱导涡核处产生非常复杂的空化结构,流场的稳定性遭到破坏;吸力面叶片顶部的叶顶间隙涡和尾部的附着空化之间的相互干涉对性能断裂起关键作用[16]。国内的一些学者也对轴流泵内的空化流动现象的研究进行了跟进。张德胜等[17]通过试验和数值模拟的方式发现了轴流泵在不同空化数下,叶片吸力面圆周截面空化面积系数从轮毂到轮缘先增大,在叶片中部达到最大值,然后迅速减小;在叶顶区由于受到间隙效应的影响,叶顶区空化面积迅速增大。沈熙等[18]对不同流量下轴流泵叶顶间隙涡和叶顶泄露涡进行了研究,发现小流量工况下更易发生空化初生,且叶顶空化形态更不稳定。

分析近年来关于喷水推进泵的研究可知,当前大部分研究着眼于轴流泵内空化流动的结构特征描述及空化流动结构对空化性能的影响,而较少有研究揭示非定常空化流动对混流式喷水推进泵的非稳态激励作用以及非定常空化诱导产生的振动特性。

非定常空化流动诱导的振动信号本质上是一种非稳态信号[19]。希尔伯特黄变换(Hilbert-Huang transform, HHT)是一种针对非稳态信号有效的时频分析方法[20]。为研究非定常空化流动诱导的喷水推进泵振动特性,本文以一混流式喷水推进泵为模型引入了HHT处理不同空化流态时的喷水推进泵振动信号,分析不同空化流态特征下的振动信号特征,探索了不同空化流态下对振动特性的影响,为降低空化加剧的振动提供参考。

1 试验方法与数据采集

1.1 试验泵与试验装置

为了研究喷水推进泵非定常空化诱导的振动特性,在中国船舶及海洋工程设计研究院喷水推进国家重点实验室的闭式试验台上进行了模型泵试验。模型泵基本参数如表1所示。

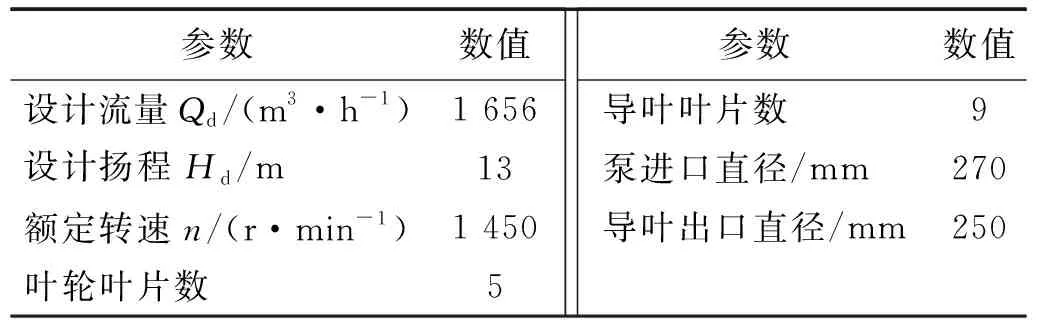
表1 测试泵的基本参数Tab.1 Main parameters of test pump

如图1(a)所示为模型泵三维示意图,模型泵的组成部件有:进口吸入管、导流帽、叶轮、导叶体、出流管。如图1(b)所示为模型泵试验现场测量布置。

图1 试验泵与试验布置Fig.1 The test pump and test rig

高速摄像是分析泵内空化流动结构演变的重要方式。通过在叶轮外壳开设有机玻璃可视窗口,采用高速摄像技术观察空化发展过程中的空化流动结构。具体的测试泵与相机布置方案见图1(b),拍摄方向与轴向成90°布置,相机镜头到观察窗的距离约为0.5 m,拍摄区域充满整个相机画幅。采用PCOS高速摄像机进行喷水推进泵叶顶空化图像采集,该摄像机在分辨率1 008 Px×1 008 Px下拍摄帧率可达4 467帧/s。为观察泵内的空化流场的瞬态特性,本试验中叶轮每转过2°拍摄一次,拍摄帧率设置为4 350帧/s。泵内非定常压力脉动信号由压力脉动传感器测得。在转轮室壁面上采用“齐壁式”安装方式安装PCB S112A22型高频压电式传感器进行压力脉动信号的采集。定义一个弦长系数λ(λ=s/c)表示叶片上的相对位置,式中:s为该位置距离叶片前缘的距离;c为弦长,为前缘(LE)到尾缘(TE)的距离。压力脉动传感器的安装位置位于叶轮上游约20 cm处和λ≈1/4,λ≈1/2,λ≈3/4的位置,将几个测点位置按照流体轴向流动的方向排序依次记作P1,P2,P3,P4;压力脉动的采样频率为51 200 Hz。非定常激励诱导的振动信号由振动加速度传感器测得;在叶轮和导叶的连接法兰上安装KISTLER 8688A50三轴加速度传感器,其中X向垂直于地面,Y向平行于泵轴,Z向平行于地面且垂直于泵轴;振动信号的采样频率为12 800 Hz。使用SIEMENS的LMS SCADA Ⅲ型多移动式数据采集系统,该系统支持32通道动态信号采集,每通道的采样频率最高可达102.4 kHz,最大数据传输率可达2.2 M采样点/s,总体动态范围优于180 dB。在测试时高速摄像系统与数字信号采集系统同时工作。数字采集系统同步采集压力脉动信号、振动信号,每采集一组数据进行实时分析,确保数据正确。

试验中其他辅助仪器有电机、扭矩仪、出口压力表、进口压力表、汽蚀筒、真空泵、调节阀、电磁流量计、增压泵、稳压筒、控制阀。其中流量计、进口压力传感器、出口压力传感器、扭矩仪的误差均为0.2%以内。

1.2 试验原理与试验方法

泵空化试验的原理是,在给定的转速和流量下,泵的必须汽蚀余量(net positive suction head required,NPSHr)是定值,而装置有效汽蚀余量,即可用的净正压头(net positive suction head available,NPSHa),会随装置参数而变化,通过调整装置的参数来改变泵内的空化流动状态。通过在叶轮外壳开设的有机玻璃可视窗口,采用高速摄像技术观察可视窗内空化发展过程中的空化流动结构的瞬态特性。试验中使用的有机玻璃窗口的折射率与清水相近,形状为外方内圆以减少由外壳与内壁之间光的二次折射引起的试验误差。

本试验采用了主动空化的方法迫使泵内发生空化。具体操作为从常压开始,通过使用真空泵降低喷水推进泵进口压力,来逐渐减小装置有效汽蚀余量,达到泵内逐步空化的目的。装置有效汽蚀余量是泵入口处流体单位质量的总能量和蒸发能量之间的差。当泵进口压力表显示进口压力稳定后,开始进行高速摄像试验和压力脉动信号、振动信号的同步采集。空化试验进行至泵扬程下5%结束。重复上述操作确定试验的可重复性,以获得准确的试验数据。通过对同步测得的瞬态流场、压力脉动和振动进行分析,建立起流场特征,非稳态激励,振动之间的联系。

2 HHT时频分析方法

HHT对获得的振动信号进行处理过程主要包括两步:首先是基于验模态分解(empirical modal decomposition, EMD)对原始信号进行分解,然后对EMD处理后的信号进行Hilbert变换。EMD方法与基于傅里叶变换的信号处理方法不同,它是直接针对数据的、自适应的和不需预先确定分解基函数的非平稳信号分析方法。EMD方法主要过程是通过提取信号的极值点信息,构建信号的包络,当前信号的包络即为该阶次的内蕴模式分量(intrinsic mode function, IMF),通过原始信号逐步减去包络信号,实现各阶的IMF提取,直到最后的信号再无极值,分解完成。EMD 是用波动上、下包络平均值确定“瞬时平衡位置”的方法,分解过程相当于对原始信号进行分频滤波,最终得到不同频段的特征信号。

EMD 分解方法是基于信号局部特征的时间尺度,把信号分解为若干个IMF之和。由于分解出的各个 IMF 突出了数据的局部特征,因此是一种新的时频分析方法,可以有效地提取出原信号的特征信息。另外,由于每个IMF 所包含的频率成分不仅与采样频率有关,而且更为重要的是它还随着信号本身的变化而变化。因此该方法具有自适应性、正交性与完备性及 IMF分量的调制特性等突出特点,在众多领域被广泛应用[21-22]。

HHT的主要步骤如下[23]:

步骤1通过 EMD 方法,信号x(t)被分解成一系列的IMF分量,可表示为

(1)

式中:imfi(t)为分解获得的第i个IMF;rn(t)为经分解得到的n个IMF后的信号残余分量,常常代表着信号的直流分量或信号的趋势。

步骤2对分解后的每一个IMF分量做Hilbert变换,假定IMF分量信号为X(t) ,则其Hilbert变换为

(2)

反变换为

(3)

得到解析信号

Z(t)=X(t)+jY(t)=a(t)ejφ(t)

(4)

式中,a(t)和θ(t)分别为信号X(t)的瞬时振幅和瞬时相位。

(5)

(6)

由瞬时相位可得信号的瞬时频率ω(t)

(7)

步骤3对每个IMF分量进行Hilbert变换,得到信号s(t)瞬时振幅在频率-时间平面上的分布,即

(8)

式中,ω(t),Ai(t)均为时间的函数,可以构成时间、频率、振幅的三维时频谱图,精确描述信号在时间段频率和振幅随时间的变化,为Hilbert时频谱,表示为H(ω,t)。

通过对Hilbert 时频谱在时间轴上进行积分可以进一步得到边际谱。定义Hilbert边际谱h(f)

(9)

边际谱反映了每一个频率点上的总幅值分布,从统计观点上来看,它表示了该频率上振幅(能量)在时间上的累加,能够反映各频率上的能量分布。

3 试验结果分析

本文的目的在于同步获取喷水推进泵内的非定常空化流动结构和压力脉动、振动信号,分析非定常空化流动诱导喷水推进泵振动特性。

3.1 空化性能试验结果

关于非定常空化可能出现的空化流动结构形式已经在翼型空化研究和轴流泵空化研究相关文献中有详细的描述,具体包括:一直存在于叶顶间隙内叶顶间隙空化(tip clearance cavitation, TCC);叶顶泄露流引起的叶顶分离涡(tip separation vortex, TSV);叶顶泄露流在叶片吸力面形成的叶顶泄露涡空化(tip leakage vortex cavitation, TLVC)。由试验观察可知,叶顶泄露空化涡随着空化程度的演变可以由丝带状,发展成片状、云状。根据试验测量结果计算随汽蚀余量变化过程中的扬程大小,绘制空化性能曲线如图2所示。由图2可知,当空化未发生时测得扬程为13.12 m,当汽蚀余量下降至7.1 m时扬程下降约5%,结束试验,过程中流量维持恒定不变。结合扬程变化情况和空化流动特征结构在空化性能曲线上选取A～E五个点代表不同的空化程度,如表2所示。

图2 设计工况下喷水推进泵空化性能曲线Fig.2 Cavitation performance curves of the model pump under design flowrate

表2 空化程度分类表Tab.2 Cavitation degree classification table

当空化处于空化性能曲线上的A,B时,扬程几乎没有下降,但此时已经具有一些不同特征的空化结构,这将在下文进行详细描述;当进口压力持续降低,汽蚀余量持续下降至C,D,E时,扬程分别下降约1%,3%和5%。

3.2 空化流场结果分析

如图3所示,为不同空化程度下的拍摄的叶顶流动结构。在叶片吸力侧和压力侧之间压差的作用下,高压侧流道经叶顶间隙泄露至低压侧,产生泄露流。因此,泄露流的运动方向与叶片的旋转方向相反。叶顶泄露流受到叶顶的剪切作用而涡度增加,形成泄露涡。叶顶区主要存在叶顶间隙空化与泄露涡空化两种不同的空化形式。随着空化程度从A发展至E,这两种空化形式又有所演变。在空化程度A时,泄露涡核心处因压力低而发生空化,形成泄露涡核心空化,主要呈现出丝带状。随着进口压的下降,细小的泄露涡核心空化丝逐渐连接成一整片的泄露涡空化;当汽蚀余量下降到B时,空化区的尾部在回流的高压流体的作用下被抬起。空化区尾部在泄露流的卷吸作用下具备相对较大的旋转速度而与整体断裂;当汽蚀余量继续下降至C时,泄露涡卷吸着吸力侧空化,形成大尺度云状空化涡,云状空化涡的尾缘开始发生小尺度的脱落,脱落的空化云在泄露流的卷吸作用下垂直向相邻叶片压力面运动,在流道中的逆压梯度的作用下脱落的小尺度的空化云未能运动到相邻叶片就被耗散在流道中;当汽蚀余量继续下降至D时,空化云尾部有大尺度的空泡脱落并运动至下一叶片压力面附近,形成大尺度的垂直空化涡(perpendicular cavitation vortexes, PCVs);当汽蚀余量继续下降至E时,稳定的大面积云状空化覆盖了叶片大部分表面,空化云尾部垂直空化涡尺度进一步增大,且空化云基本覆盖叶片吸力面叶顶区域。垂直空化涡的发展能够较好的反映空化流场的非定常性。

如图4所示为严重空化 时不同时刻空化流场图。由图4可以看出空化流场是非定常的,随着时间的推移,大尺度垂直空化涡从空化云尾部脱落,逐渐运动到相邻叶片的压力面,最后在叶片压力面附近崩溃。

图4 严重空化状态下空化流场的非定常演化Fig.4 Unsteady cavitation flow structure at severe cavitation state

3.3 压力脉动信号

通过压力脉动传感器测得监测点处的压力脉动。为消除监测点自身静压对压力脉动的影响,用压力系数Cp表示监测点压力脉动。压力系数表达式为

(10)

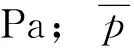
相比于P1和P2,P3和P4处流动更加复杂,压力脉动受到动静干涉和空化的影响较其他点的变化更为明显。如图5所示为P4点处压力脉动时域图,由图可知,压力脉动整体上呈周期性波动,周期为一个叶轮通道扫过传感器的时间,说明叶轮周期性旋转导致的动静干涉作用是影响压力脉动的主要因素。压力脉动波峰和波谷之间的差值也随着空化程度的加剧有所增加,可见空化是压力脉动增加的重要原因。另外一方面随着空化程度的加剧,压力脉动系数且呈现出越来越剧烈的不规则的波动。压力脉动波形图上的最小值随着空化程度的加剧而下降,反映了叶片吸力面的压力随着空化程度的加剧而进一步降低,这也是导致空化流动结构演变、空化云面积增大的重要原因。压力脉动波形图上波谷区持续的时间也随着空化程度的增大而增大,反映了空化区的面积随着空化程度的增大而增大。在压力脉动从最小值上升时,出现了周期性的冲击信号,带来了压力脉动迅速的增大后又回归正常值,这可能是空化云的尾缘与非空化区交界处产生的局部冲击,当这一区域略过传感器时导致了压力脉动信号的迅速上升。

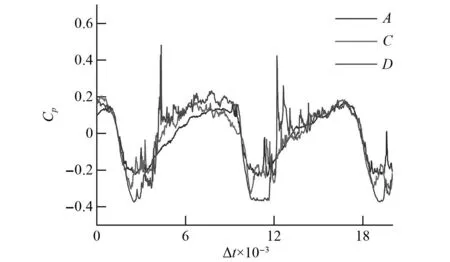
图5 不同空化程度下压力脉动时域图Fig.5 Time domain diagram of pressure fluctuation at point 4 under different cavitation levels

3.4 振动信号分析

3.4.1 时域分析

如图6所示为测点处X向上不同空化程度下的振动加速度时域对比图。由图6可知,随着空化程度的增加,振动加速度幅值呈现出增大趋势。Y向和Z向振动也呈现出与X向相似特征。可见空化会严重加剧喷水推进泵的振动。

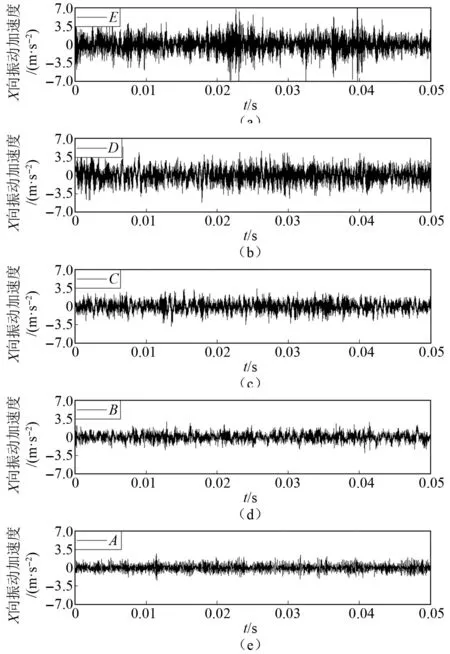
图6 振动信号时域分布图Fig.6 Time domain distribution of vibration signal

均方根是信号的二阶矩,常用来表征信号的平均能量,计算公式为

(11)

式中,Xk为信号的测量值,k=1,2,…,N。

图7为试验泵在不同汽蚀余量下的不同方向上的振动信号均方根随空化程度变化图。

由图7可知,不同方向上的振动强度整体上是随汽蚀余量的减少而增加,可见空化是促进了泵在各个方向上的振动。不同方向上,片状空化发展期间(A～B)及云状空化发展初期(B～C)振动总体能量增速相对缓慢。云状空化发展到一定程度(C)后,三个方向上的振动信号随空化程度的加剧而增速增大。流动产生的激励:一是会直接作用于转轮室上;二是作用在叶轮叶片上,再通过转子轴系的传递最终造成整个泵体的振动。安装于转轮室上的动态压力传感器可以很好地直接捕捉到转轮室内壁受到的径向的压力信号的脉动情况,结合图4可以分析得出,当空化云发展到C后,由空化产生的非平稳压力脉动信号显著增大,这可能是导致径向(X向和Z向)振动信号增速增大的主要原因。而轴向振动在扬程下降前,并未明显增长;在扬程下降1%过后,轴向振动信号的能量显著增大;空化程度达到临界空化后增速进一步变大。导致轴向振动能量变化的主要原因在于轴向的激励变化,轴向的激励与空化云的发展密切相关。刚开始增速较小的原因在于丝状、片状的空化涡对于轴向流动堵塞作用较小,而且此时少量空泡的破碎不会产生强烈的冲击力作用在叶片和转轮室上。空化云及小尺度的垂直空化涡产生后,在一定程度上堵塞了轴向流动,同时吸力面上空化云的聚集改变了叶片表面的压力,这些可能是造成轴向振动增大的主要原因。当大面积的云状空化结构产生后,空化体积的大程度的增长以及垂直空化涡的形成造成了叶轮通道内流体的大面积堵塞,从而产生了较大的非平衡力,同时大量的气泡的非定常演化会叶片表面和转轮室内壁面的形成较大的非定常激励,诱导了轴向的振动信号的迅速增大。

3.4.2 频域分析

通过快速傅里叶变换(fast Fourier transform,FFT)对时域里的振动信号进行处理,可以得到振动信号的频谱分布。傅里叶频谱描述了整个采样时间里出现过哪些频率及这些频率对应的幅值。将频率表示成轴频(fn)倍数得到如图8所示的频域分布图。临界空化是工程中最为关注的状态,图8(a)为未空化状态,图8(b)为临界空化状态下的振动信号频域分布。其中由图8(a)分析得知,当空化还未发生时,主频为轴频,离散峰值主要有轴频、叶频、2倍/3倍/4倍叶频;临界空化时,信号在整个频域区间上的振幅都有较大增幅,信号的主频为叶频,在轴频、3倍、5倍叶频处也存在明显的峰值。

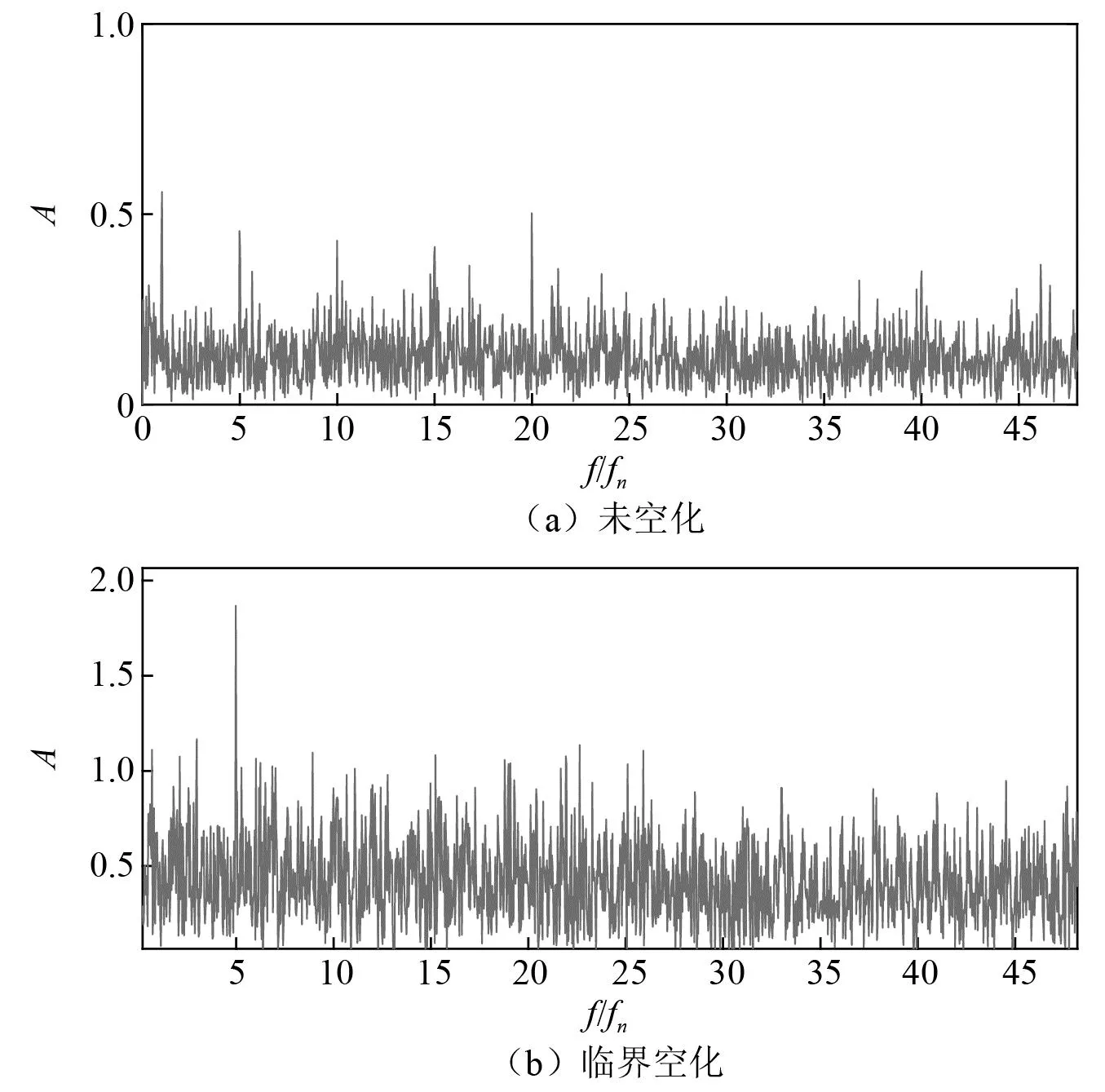
图8 振动信号频域分布Fig.8 Frequency domain distribution of vibration signals

非空化状态下,动静干涉作用是压力脉动的主要来源,压力脉动的主频为叶频。动静干涉作用也是非定常流动产生的重要因素,非定常流动产生的激励是喷水推进泵振动的重要激励源。同时非定常激励也会作用在于叶片上,带动叶片旋转,叶片受到的非定常激励也会传递至轴系上,造成轴系振动,并传递至泵体上。当泵发生空化时,叶频处的振动明显增强,这说明空化会在很大程度上加剧周期性压力波动的不稳定性,导致特征频率处产生较大的激励。另外一方面,空化流动结构复杂,这些流动结构也会随着时间演变,在不同的时刻x也会产生非稳态激励信号,加剧泵体在整个频域里的振动。

3.4.3 基于HHT的泵振动信号时频分析

空化状态下的流动是一种非稳态流动,空化结构在空间位置的产生、消失具有一定的瞬态特性,产生的激励也是非平稳激励。这意味着这种激励信号里包含一定的随机成分,频率在时间上具有一定的时变性。傅里叶变换是一种对全局处理方法,能得到信号在频域里的全局分布。但这意味着信号的傅里叶频谱特征中,无法判断某一频率的信号是长期还是短暂出现在信号整体中,因此FFT难以判断出信号的瞬态特性[24]。

HHT是基于信号的局部特征,自适应的筛选出模态函数分量,既能克服FFT只能得到信号某一段时间内的频率的均值信息而无法准确描述时频分布的缺点,也能避免小波分析中对小波基选择的困难而造成的自适应性低的问题。HHT变换主要包括EMD和Hilbert变换两个步骤。图9为X向未空化时的振动信号进行EMD分解后的各阶模态分量对应的时域分布图,为控制分解后的残差以保证分解得到后的各阶分量能充分反映原信号的信息,确定最终的分解模态数为9。

由上述频域分析可知,空化发生后,产生的空泡体积差异较大,对应不同的溃灭频率,会导致宽频范围内的冲击,并最终会导致振动信号在很宽的频域范围内均有所上升[25]。相比于其他模态,第一阶模态(imf1)涵盖了最宽的频域范围。为分析空化对整个宽频范围内的影响,选取imf1进行分析,根据式(1)计算不同程度下的imf1有效值可得到如图10所示的imf1能量随空化程度的变化情况。

图10 不同空化程度下的一阶模态均方根Fig.10 RMS of imf1 with different cavitation levels

由图10可知,随着空化程度的加剧,imf1的均方根值也随着增加。片状空化尾部会存在快速的小尺度脱落,引起水力激励的高频脉动分量[26],因此在泵内的片状空化产生及发展过程中(A～B),imf1的能量增幅达0.57倍。当片状空化发展到一定程度时破裂形成空穴界面波动的云状空化[27],云状空化阶段大尺度云空泡溃灭也会产生高频宽频的空泡溃灭脉冲。在喷水推进泵中,当空化发展到临界空化时,产生了大尺度的垂直空化涡运动到叶片压力面发生溃灭,产生高频脉冲,所以在空化初生到临界空化状态时,imf1的均方根也有较大增长,可见垂直空化的发展对喷水推进泵的振动有着重要影响。

根据式(7)计算出Hilbert谱在时间域上的积分,得到X向的振动信号的希尔伯特边际谱,如图11所示。其中y坐标轴表示该信号的某一频率在全部时间内的能量总和,横坐标表示的信号的频率。对比信号的Hilbert边际谱与信号的FFT频谱可知,二者存在很大的不同。Hilbert边际谱反映了振动信号的能量主要集中的低频部分,可见泵内流激振动主要还是集中在低频部分。振动信号的希尔伯特边际谱中轴频是主频,叶频是次主频,因此叶轮旋转是喷水推进泵产生振动的主要原因。高频部分信号的能量远小于低频部分。空化状态片状空化发展期及云状空化形成期(从A～C),高频部分(大于4倍叶频)有些增长,低频部分(低于4倍叶频)增幅相对较小。吸力面云状空化充分发展后,一方面改变了叶片表面的流体分布和压力分布,造成了吸力面的压力的下降和压力波动的增大;另一方面空化云尾缘出现低频脱落形成垂直空化涡,低频的脱落造成了压力的低频波动,而空泡的破碎又造成了冲击带来了高频成分,最终在B～D阶段造成了低频振动和高频振动均出现了较大增幅。片状空化发展期(A～B),主频幅值约增长了23.4%,次主频幅值增长了31%;垂直空化涡发展期(C～D)主频幅值增长了约64.7%,次主频幅值增长了87.6%。

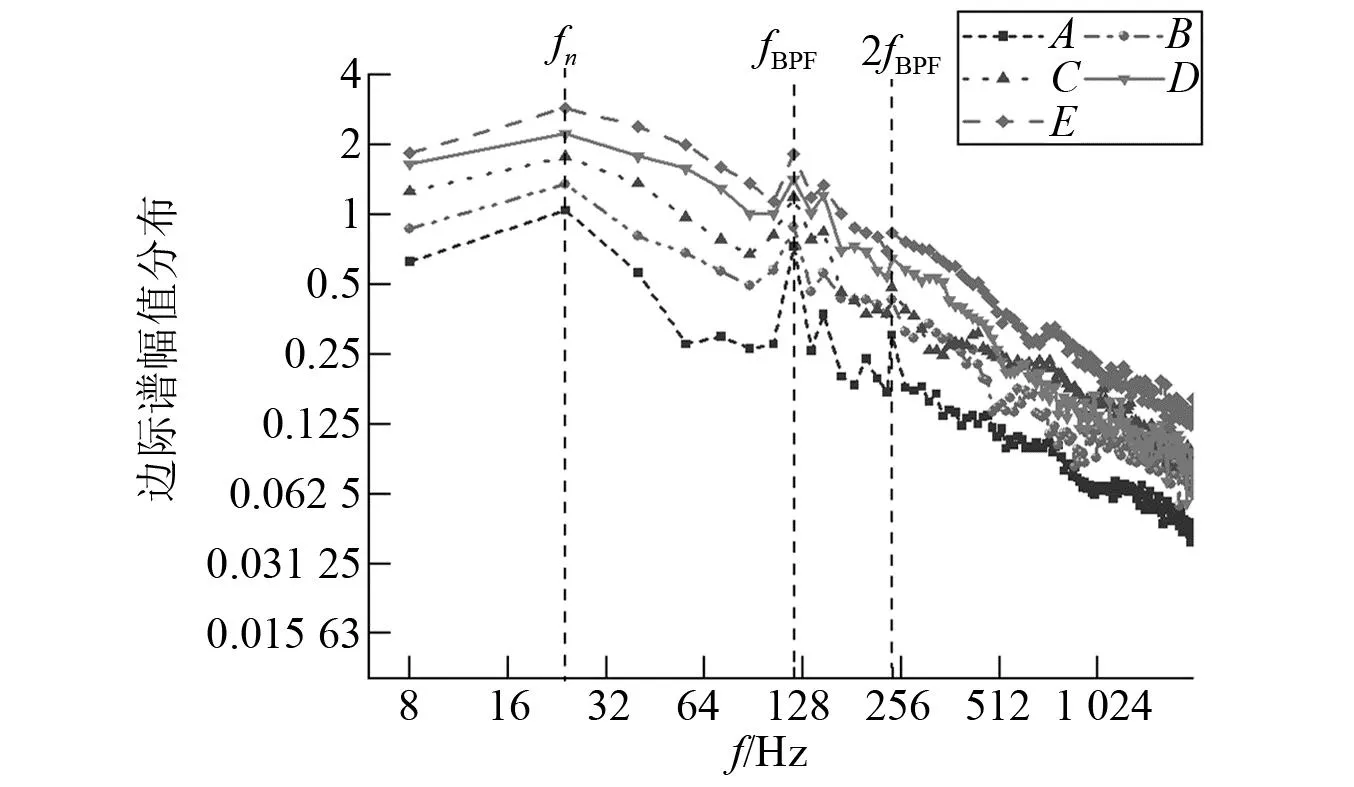
图11 X向振动信号边际谱Fig.11 Marginal spectra at direction of X under different cavitation levels

由希尔伯特边际谱可知空化会严重加剧喷水推进泵的振动,且相比于快速傅里叶频谱,希尔伯特边际谱的变化可以更好地反映泵内的空化流动情况。造成这种Hilbert边际谱与FFT频谱在分布上特征不同的根本原因在于空化流动诱导的振动信号本质上是非平稳信号,信号包含的频率随时间而改变。傅里叶变换后得到的频率是分布在整个时间尺度内的正弦或余弦分量,而边际谱中横坐标对应的频率和傅里叶变换所得的横坐标上的频率有所不同,Hilbert边际谱是幅值、频率和时间的非归一化联合加权分布。分配给每个单位时频分量的权重为 Hilbert 谱的局部幅值。相比于傅里叶频谱,Hilbert边际谱中包含了频率在时间上的加权平均,因此能反映信号的时频特性。通过HHT处理和分析喷水推进泵的振动信号,能够在一定程度上更好的认识喷水推进泵空化流动引起的非定常激励特性。

4 结 论

(1) 喷水推进泵会发生由于叶顶间隙涡导致的间隙空化和叶顶泄露涡导致的叶顶泄露空化;叶顶泄露涡空化会随着空化程度的加剧,呈现出丝状、片状、云状结构;随着空化程度的进一步加剧,云状空化尾部会脱落形成垂直空化涡向下一叶片的吸力面运动,将堵塞流道并造成压力面做功能力下降,并导致喷水推进泵性能的下降。

(2) 随着汽蚀余量的降低,云状空化发生前,压力脉动和振动都是缓慢增加;云状空化堵塞流道,造成压力脉动和振动的迅速增大;云状空化尾部大尺度的空泡团脱落造成的垂直空化云是低频振动迅速增大的主要原因。

(3) 通过Hilbert-Huang对振动信号进行时频域分析可知,流动诱导振动的能量主要集中在低频部分,空化会改变泵内的压力分布,空化云尾缘出现低频脱落形成垂直空化涡,低频的脱落造成了压力的低频波动,而空泡的破碎又造成了冲击带来了高频宽频成份;Hilbert边际谱中轴频和叶频处的振动幅值能较为准确的反映空化的发展程度。