基于高斯展开法的碟形声学黑洞宽频调谐减振机理研究

丁 媛, 施凯耀, 郑 玲

(重庆大学 机械与运载工程学院 机械传动国家重点实验室,重庆 400044)

声学黑洞[1]是利用薄壁结构几何参数或者材料特性参数的梯度变化,使波在结构中的传播速度逐渐减小,理想情况下波速减小至零从而不发生反射的现象。由于其在减振降噪[2-3]、能量回收[4-7]以及声波调控[8-10]方面的应用潜力,在过去的十几年中一直倍受关注。

Zeng等[11]研究了不同截面形状一维声学黑洞梁的能量聚集效应,分析了激励位置对声学黑洞不同频率段能量聚集的强化作用,提出了声学黑洞梁宽频振动控制的影响因素。黄薇等[12]对嵌入二维声学黑洞的薄板进行了能量聚集效应研究,试验证明了声学黑洞结构对聚集波动能量的科学性与有效性。Ji等[13]针对具有尖端截断的非完美一维声学黑洞梁,试验测试了声学黑洞梁的反射系数,通过在声学黑洞能量聚集区域引入阻尼层,弥补了尖端截断带来的聚能效应衰减问题。但以上嵌入式声学黑洞,存在局部结构强度弱化问题,影响其工程实用性。

Deng等[14-15]研究了带加强肋的声学黑洞(acoustic black holes,ABH)环型结构,研究表明,多个环形ABH可以有效降低中心激励源的振动传递,加强肋不仅改善了环形ABH的结构弱化,对降低振动传递也有显著效果。Zhou等[16]将两个ABH梁在ABH中心位置进行正向或反向重合,构建了复合ABH梁,有限元分析表明,复合ABH梁相比传统的单个嵌入式ABH梁,其振动抑制作用明显增强,且局部结构弱化问题得到有效改善。Gao等[17]在上述复合ABH梁基础上,在声学黑洞的两端嵌入了乙烯-醋酸乙烯酯(ethylene-vingl acetate,EVA)材料,改善了其低频振动控制的效果。

为了克服嵌入式声学黑洞存在的局部结构强度弱化问题,Ji等[18]设计了一种二维圆形ABH,将其附加在主体结构上以抑制主体结构的振动。Comsol有限元分析和试验表明,由于ABH和主体结构的耦合作用,其主体结构的振动得以有效抑制。本文设计一种新的二维碟形声学黑洞结构(dish-shaped acoustic black hole,DABH),将其附加在主体结构上,以实现对主体结构的减振。基于高斯展开法,建立其半解析分析模型,分析碟形声学黑洞与主体结构的耦合作用,揭示其宽频调谐减振机理,为拓展声学黑洞在宽频结构振动控制上的应用提供新的设计思路。

1 二维碟形声学黑洞耦合系统建模

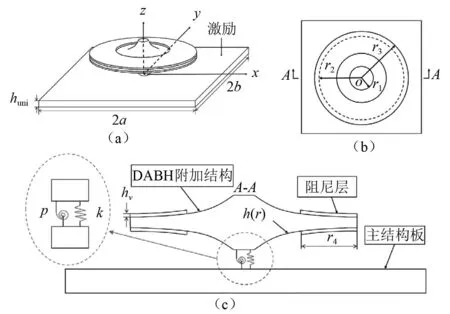
图1 DABH附加结构与耦合系统结构图Fig.1 DABH and its coupling system structure

实际情况中,DABH是通过螺栓或焊接安装到主结构板上,因此两个部件在连接点处具有相同的位移和旋转角度。一般处理边界条件的方法有人工弹簧法[19-20]和零空间法[21-22]。本文连接部分使用人工弹簧来模拟,平移弹簧刚度为k,旋转弹簧刚度为p,如图1(c)所示。

本文基于Rayleigh-Ritz法框架,选择高斯函数作为基函数,根据碟形声学黑洞板的形状确定高斯基函数的分布,建立碟形声学黑洞与主结构板耦合系统的半解析分析模型。采用Comsol软件,建立其有限元模型,验证其正确性。

1.1 二维基函数的选取

DABH和主板结构三个方向的位移可由一系列二维形函数线性叠加来表示

(1)

式中:w,u,v分别为z方向的面外位移以及x和y方向的面内位移;φi,ξi,χi为形函数向量;Wi,Ui,Vi为权重向量;i=1为主结构板;i=2为DABH。耦合系统的形函数向量ξ和权重系数向量q分别为

(2)

以面外位移w的形函数φi为例,描述其具体形式,面内位移u,v与之类似。φi可由克罗内克积表示

φi=φix(x)⊗φiy(y),i=1,2

(3)

式中:φix(x)为x方向的形函数;φiy(y)为y方向的形函数,即

(4)

(5)

式中:px,py分别为x方向和y方向的尺度因子,其决定了半解析模型的计算精度;qxj和qyk分别为x方向和y方向的平移因子;m为φix(x)中元素的个数;n为φiy(y)中元素的个数。结合式(3)和式(4),可以得到

(6)

由式(6)可知,形函数向量φi的维度为mn。其中,尺度因子和平移因子的选取需满足[23]

(7)

qxj=[-4+floor(-2px·a),ceil(2px·a)+4]

(8)

qyk=[-4+floor(-2py·b),ceil(2py·b)+4]

(9)

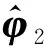
(10)

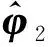
1.2 二维碟形声学黑洞耦合系统半解析模型

在Rayleigh-Ritz框架下,可建立耦合系统的拉格朗日方程,导出耦合系统的运动方程。主结构板和DABH的动能为

式中:ρi(i=1,2)为两者的密度;hi(x,y)(i=1,2)为两者的厚度。系统总动能为

(12)

式中,M为耦合系统的质量矩阵。

系统的势能由三部分组成,主结构板和DABH的势能以及连接处的弹性势能。主结构板和DABH的势能为

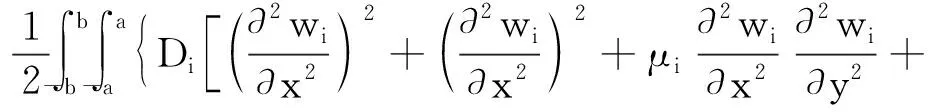
(13)

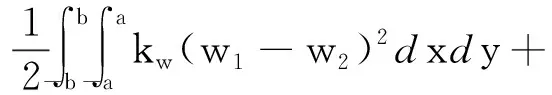
(14)

最终耦合系统的总势能为

(15)

式中,K为耦合系统的刚度矩阵。

对主结构板施加外力,系统的外力功可表示为

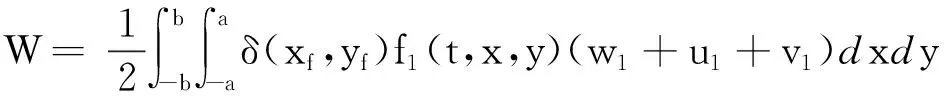
(16)

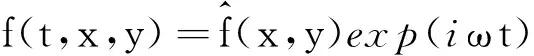
W=qTf

(17)

式中,f为外力在以高斯基函数为广义坐标下的力向量。

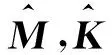
利用式(12)、式(15)和式(17),可建立拉格朗日函数

(18)

欧拉-拉格朗日方程为

(19)

由此得到耦合系统的运动方程

(20)

将q=Qexp(iωt)和f=Fexp(iωt)代入上式,可得运动方程的频域表达式

(21)

进一步,令F=0,式(21) 成为一个广义特征值问题,可求解出耦合系统的特征频率ωn和特征向量Qn。

1.3 模型验证

为了验证所建立的半解析模型的准确性,基于Comsol有限元分析软件,建立DABH与主结构板耦合系统的有限元分析模型,将半解析模型与有限元模型的计算结果进行对比。二维碟形声学黑洞耦合系统如图1所示,主结构板边界条件为自由边界,附加DABH与主结构板在中心处连接,相关的材料和几何参数如表1所示。主结构板和DABH采用同种材料,表中:ρ,E,μ及η分别为该材料密度、弹性模量、泊松比和阻尼系数;ρv,Ev,μv及ηv分别为铺设的阻尼材料的密度、弹性模量、泊松比和阻尼系数。弯曲波和纵波的平移弹簧系数设置为kw=1×1011N/m、ku=1×1014N/m,旋转弹簧系数为p=1×109N·m/rad。

表1 耦合系统的材料参数和几何参数Tab.1 Material parameters and geometric parameters of the coupling system

1.3.1 模态收敛性验证

图2为半解析模型与有限元模型的模态频率对比结果及其相对误差。半解析模型计算过程中,选取尺度因子为px=py=6。由图2可知,本文建立的半解析模型,其计算结果准确,与有限元模型结果的相对误差均在2%以内。

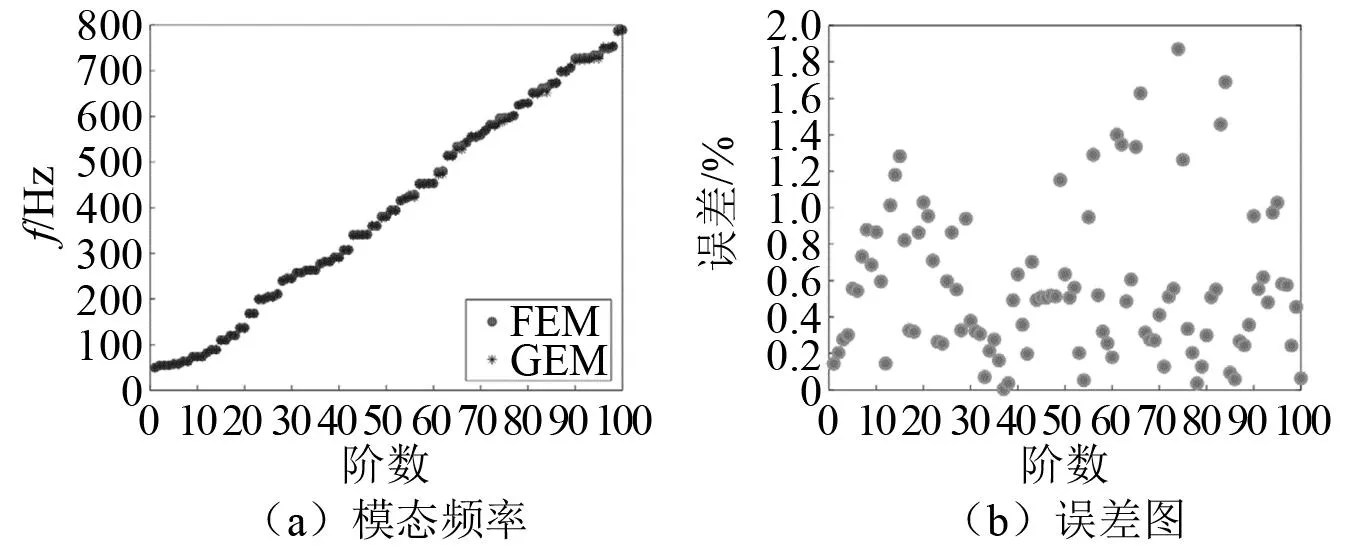
图2 声学黑洞板的模态分析结果Fig.2 The diagram of modal frequency error of the system

图3是耦合系统的模态振型图。其中:第一行为DABH高斯展开法计算结果;第二行为DABH有限元计算结果;第三行为主结构板高斯展开法计算结果;第四行为主结构板有限元计算结果。可以看出,半解析模型的第 2、第19、第31、第41 阶模态振型与有限元模态振型完全一致,验证了半解析建模方法的正确性。

图3 DABH与主结构板耦合系统的模态振型图Fig.3 Modal mode shape diagram of the coupling system of DABH and the host plate

1.3.2 强迫响应验证

对DABH与主结构板耦合系统施加正弦载荷,其作用点的坐标为(0.35,0.35),幅值为1 N(见图1(b))。计算主结构板的平均均方速度MSV

(22)

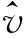
主结构板的平均均方速度,如图4所示。由图4可知,在 2 000 Hz 以内,半解析模型计算的平均均方速度(mean square velocity,MSV)与有限元模型的MSV基本吻合。

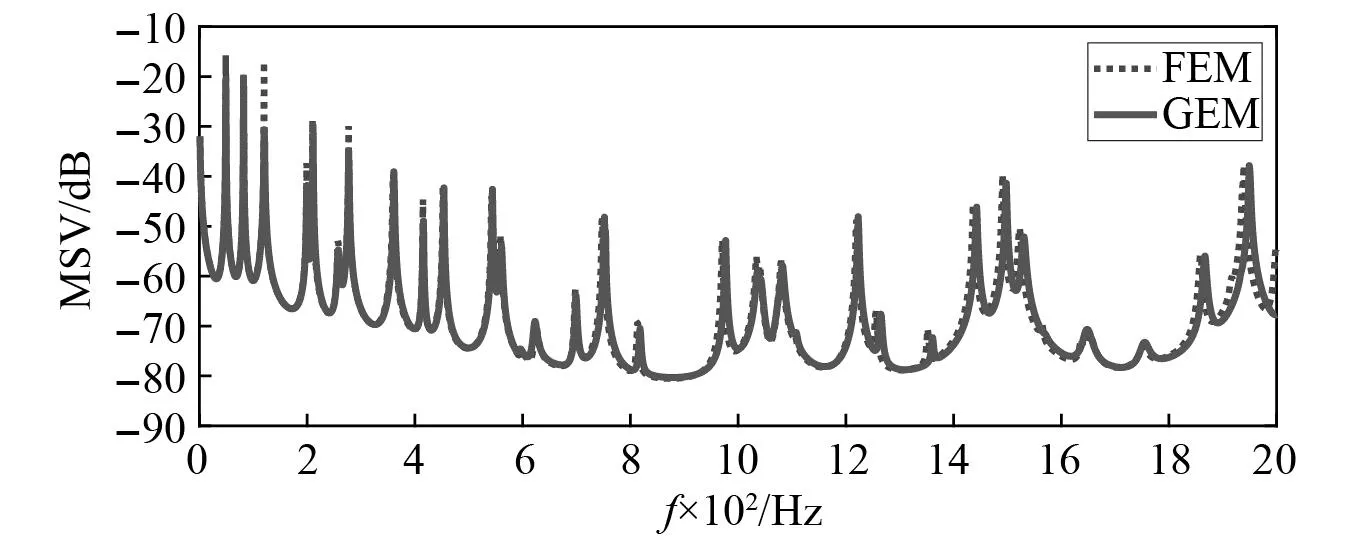
图4 耦合系统的平均均方速度Fig.4 Average mean squared velocity of the coupled system

1.3.3 计算效率验证

为了比较两种方法的计算效率,分别测试了有限元模型和半解析模型固有频率和强迫响应的计算时间。有限元模型前200阶固有频率的计算时间为1 599 s,0～2 kHz强迫响应计算时间为179 549 s,半解析模型前200阶固有频率的计算时间为427 s, 0～2 kHz强迫响应计算时间为3 463 s。结果表明,本文建立的半解析模型具有更高的计算效率,这为进一步参数优化和耦合机理分析,提供了计算手段。

2 宽频调谐减振机理

在DABH外缘粘贴阻尼层,有无DABH附加结构的主结构板强迫响应对比,如图5所示。由图5可知,DABH附加结构触发了主结构的宽频振动抑制。DABH作为一个动态吸振器,在268 Hz和580 Hz引起了峰值分裂,共振峰数量增加,单个峰幅值下降,表现出更显著的减振效果。对于其他共振峰,虽未出现峰值分裂,但出现了峰值偏移及幅值的明显降低,如370 Hz和425 Hz。上述现象产生的原因:一是由于附加结构的ABH能量聚集效应;二是DABH的动态吸振器(dynamic vibration absorber,DVA)效应。前者表现为某些共振峰值降低但未出现峰值分裂,后者表现为部分频率发生峰值分裂。此外,声学黑洞结构存在截止频率[25]

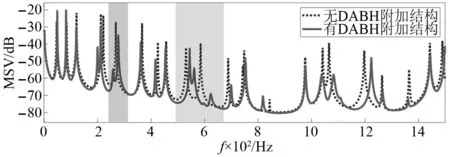
图5 有无DABH附加结构的主结构板的MSVFig.5 MSV of the host plate with or without DABH

(23)

声学黑洞效应不能被频率低于frABH的波触发。DABH的截止频率在200 Hz附近,从图5可以看到在200 Hz以下,DABH的减振效果并不明显,附加DABH的主结构板在高频表现出更显著的减振效果。

2.1 DABH结构的能量损耗及影响因素

2.1.1 DABH结构的减振作用

为了验证DABH的能量聚集效应,在DABH结构的中心施加振幅为1 N的简谐力。采用振动均方根速度(root mean square velocity,RMS velocity)对响应进行表征,RMS定义为

(24)

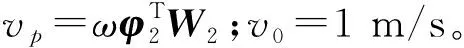
选取两个测试点,Rm1=0.17 m,位于幂律裁剪外围的均匀平台处,Rm2=0.025 m位于DABH中心的均匀平台处,如图6所示。此外,定义能量比为Γ=20lg(|vm1/vm2|),来表征声学黑洞的聚能效应。

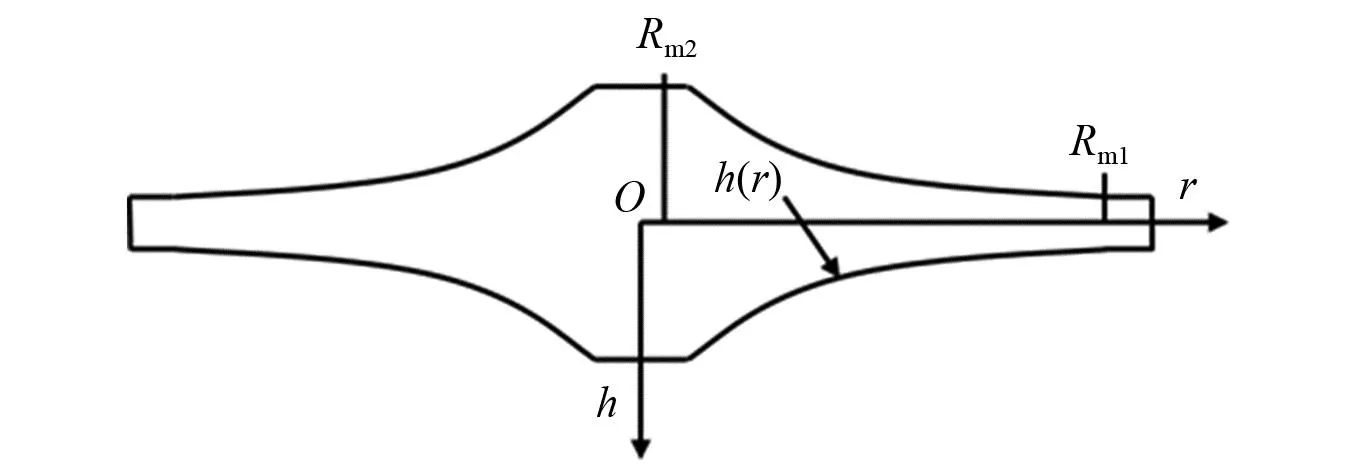
图6 点Rm1和Rm2位置示意图Fig.6 Schematic diagram of the location of points Rm1 and Rm2

为了验证ABH效应,将具有与DABH尺寸相同的圆形均匀板(uniform circular plate,UCP)的结果作为参考。由于板结构丰富的模态频率,我们仅分析0～2 kHz的振动响应。图7(a)和图7(b)分别为Rm1和Rm2处的结果对比。从中可知,与UCP相比,DABH在Rm1处的响应速度较大,毫无疑问这是由于ABH厚度幂律裁剪导致的波传播特性。理论上,Rm2处的速度响应相比UCP,其速度响应应该较小,但图7(b)表明,这种差异并不显著。表明Rm2与Rm1距离不远,仅靠弯曲波在ABH中的传递,并不能显著降低Rm2的振动响应,尚需通过某种耗散机制来进一步减少弯曲波在边界的反射。图7(c)为两点的能量比,可以看出,DABH相较于UCP的能量集中效应是十分明显的。

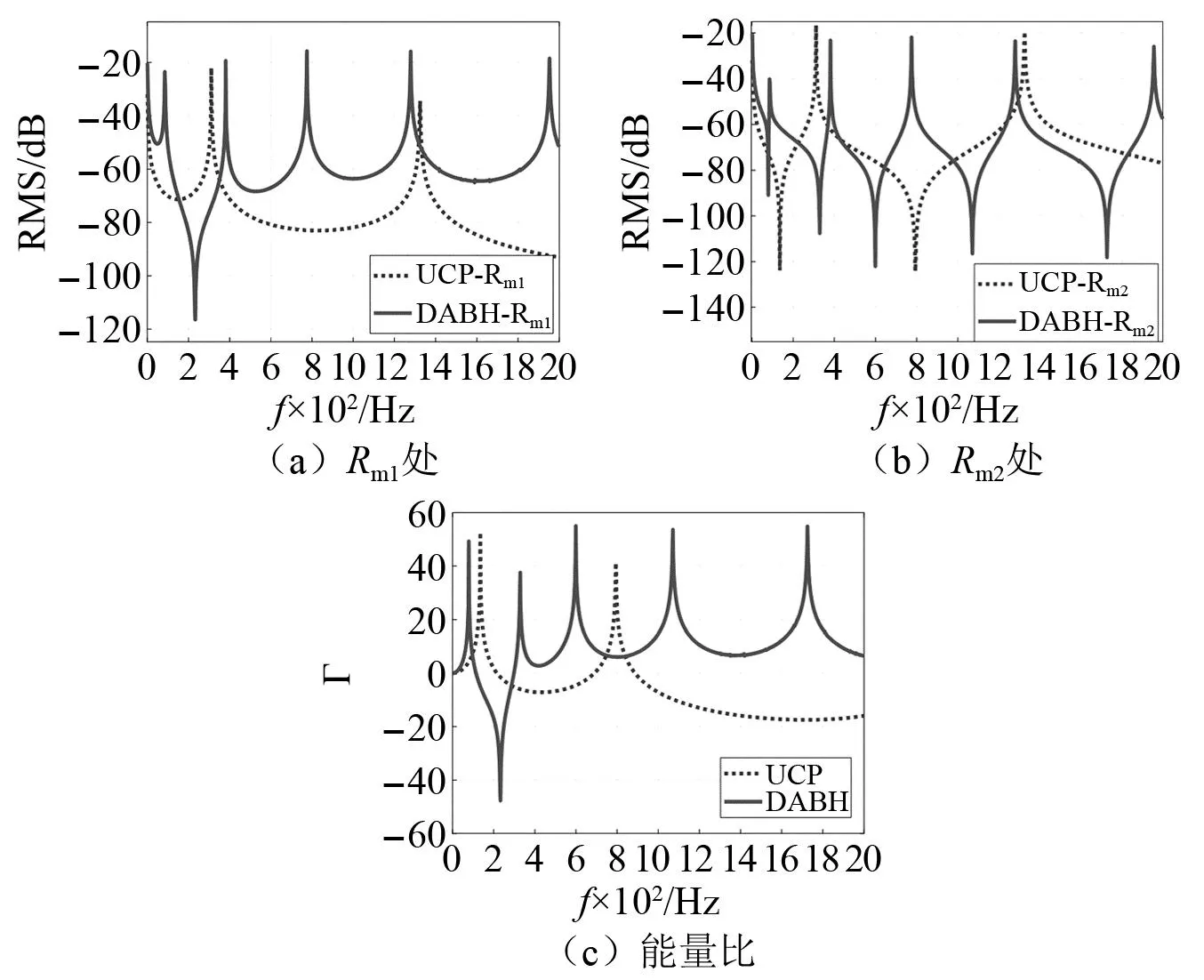
图7 DABH和UCP的振动均方根速度及能量比Fig.7 Vibration RMS velocity and energy ratio of DABH and UCP

为了耗散ABH在尖端部分的振动能量聚集,本文在尖端部分粘贴阻尼材料,以降低弯曲波在边界的反射,UCP也做同样处理。阻尼材料粘贴在DABH的r4区域,(见图1(c))。阻尼材料的几何和材料参数见表1。在DABH和UCP的中心施加振幅1 N的简谐力,比较两者的强迫响应MSV,图8(a)为强迫响应结果。可以看出,粘贴阻尼材料以后,DABH边缘的振动能量被有效耗散,共振频率处的幅值低于相同处理的UCP。图8(b)为0～1 500 Hz的模态频率和模态阻尼比,可见粘贴阻尼材料后,DABH的模态损耗因子远远超过UCP,这是由于DABH优越的能量聚集效应带来的高阻尼特性。此外,UCP仅有68个模态,而DABH则有132个模态,由于DABH模态密度增加,大大促进了DABH与主结构板耦合的几率。

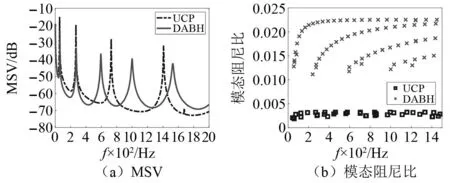
图8 粘贴阻尼材料的DABH和UCP的MSV和模态阻尼比Fig.8 MSV and modal damping ratio of DABH and UCP with damping material

将粘贴阻尼材料的DABH及UCP安装到相同的均匀方板上,连接位置与施加的激励与前述一致。图9为附加DABH及UCP的主结构板表面的MSV。可以看出, DABH触发了主结构板的宽带振动抑制。尽管附加UCP的主结构板,其部分共振峰也有所降低,但其作用与DABH相比是很小的。说明DABH作为附加结构,通过与主结构的耦合作用,利用其ABH效应以及DVA效应,实现了振动能量从主结构板到DABH的转移以及在DABH边缘尖端的振动能量耗散,达到了更好的减振效果。

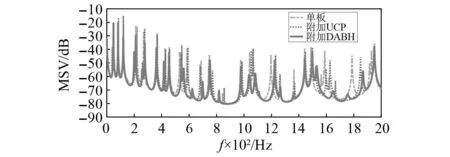
图9 附加DABH和UCP的主结构板的MSVFig.9 MSV of the host plate with DABH and UCP

2.1.2 DABH结构参数影响

从图1可知,影响DABH性能的主要参数有截断厚度he、衰减指数m、ABH半径rABH以及外延宽度r3-r2,不同参数的影响效果如图10所示。

图10 DABH结构参数对主结构板振动响应的影响Fig.10 Influence of DABH structural parameters on vibration response of the host plate

在一维ABH梁的研究中,已证明截断厚度对于ABH效应有较大的影响。非理想情况下,因为截断厚度的存在导致弯曲波从尖端反射,从而影响ABH效应。从图10(a),也可以看到DABH具有类似的效果,即随着截断厚度的减小,MSV的峰值也在不断降低,DABH的减振效果增强。

众所周知,ABH效应在剖面变化幂指数m≥2时成立。图10(b)是不同m值下DABH在5 kHz内的振动响应。可以看到,增加幂指数m对最终减振效果影响不大。

外延宽度是DABH边缘外伸的一段均匀厚度部分的宽度,即r3-r2。在图10(c)中,保持r2=0.15 m不变,通过改变r3,来获取不同的外延宽度。一维ABH的研究表明,一定的外延部分对于ABH效应的提升是有帮助的[26]。本文中DABH二维结构,也有类似的现象,即随着外延平台尺寸的增加,主结构板MSV的峰值显著降低,但降低的效果会随外延宽度的增加逐渐减弱。

假设外延宽度为零,通过改变ABH半径,来分析ABH半径的影响规律。从图10(d)中可以看到,随着ABH半径的增加,ABH减振效果增强。相比于最小的半径尺寸rABH=0.13 m,最大的半径尺寸rABH=0.17 m的主结构板MSV峰值降低了8 dB。此外,随着半径的增加,ABH效应也会向低频拓展。

除了DABH本身的参数以外,DABH的安装位置对主结构的减振性能也有影响。图11 是DABH不同安装位置的模态振型。图11(a)表明,当DABH位置处于主结构板节点位置时,其主结构板的MSV较高;图11(b)表明,当DABH处于主结构板的非节点位置时,其可以通过耦合,更多地从主结构板中吸收振动能量,并由阻尼材料进行耗散。因此,DABH安装在主结构板幅值越大的地方,对主结构板的有更好的减振效果。图12是不同安装位置的主结构板MSV,也可以观察到同样的现象。除了安装位置外,DABH的对称性也会影响减振效果[27]。

图11 DABH不同安装位置的系统模态振型(751 Hz)Fig.11 Modal shapes with different mounting positions (751 Hz)

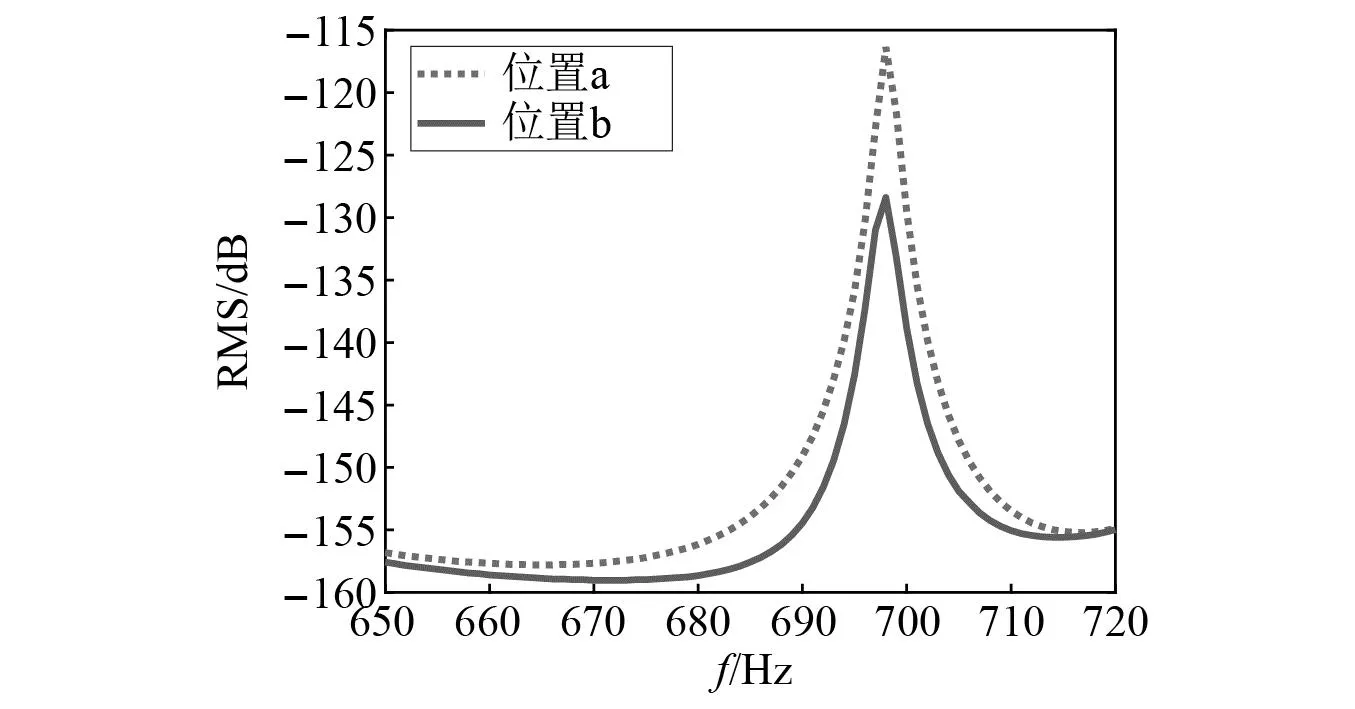
图12 不同安装位置的主结构板的振动响应Fig.12 Vibration response of the host plate in different mounting positions

2.2 模态振型对动态耦合效应的影响

图13是阻尼材料的阻尼系数设为0时,有无DABH的强迫响应结果。可以观察到,如果没有阻尼材料的耗散作用,其结构板峰值分裂现象更为明显,共振峰数量更多。相比图5,在1 040 Hz附近出现了新的峰值分裂。分析峰值分裂对应频率的DABH模态振型发现, DABH具有同心圆振型,如图14所示。这与Ji等的发现规律一致,即附加结构与主结构的强耦合仅在特定DVA模态发生。

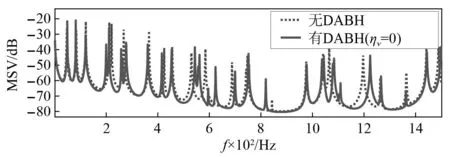
图13 有无DABH附加结构(ηv=0)的主结构板的强迫响应MSVFig.13 Forced response MSV of the host plate with or without DABH (ηv=0)

图14 DABH的同心圆振型Fig.14 Concentric circle modal shape

分析DABH模态振型可知, 在1 500 Hz范围内,共有四个同心圆模态,分别对应61.33 Hz,272.85 Hz,594.50 Hz,1 000.07 Hz。除最小的频率61.33 Hz外,其他三个固有频率均在图13中出现了峰值分裂。

图15是耦合系统以及组成部分的模态频率和模态阻尼比。将耦合系统的模态分为三类:第一类是DABH主导的模态,即耦合系统与DABH的模态频率以及模态阻尼比基本一致;第二类是主结构板主导的模态,即耦合系统的模态频率与主结构板的模态频率基本一致;第三类是产生明显耦合作用的模态,即耦合系统的模态频率与DABH以及主结构均不相同,出现了新的耦合模态,其模态阻尼比比主结构板的模态阻尼比要大。第三类的耦合模态频率中,包含了268 Hz, 580 Hz以及1 040 Hz附近频率,即图15中绿色虚线圈出的模态,它们分别对应了DABH的同心圆振型模态频率272.85 Hz, 594.50 Hz以及1 000.07 Hz, 实现了完美的DVA效应。尽管DABH有丰富的模态,但其与主结构板发生耦合的模态并不多,第一类和第二类的系统模态并未发生耦合,DABH以及主结构分别各自保持原有的模态特征,仅其中一个产生振动,另一个并不参与振动。

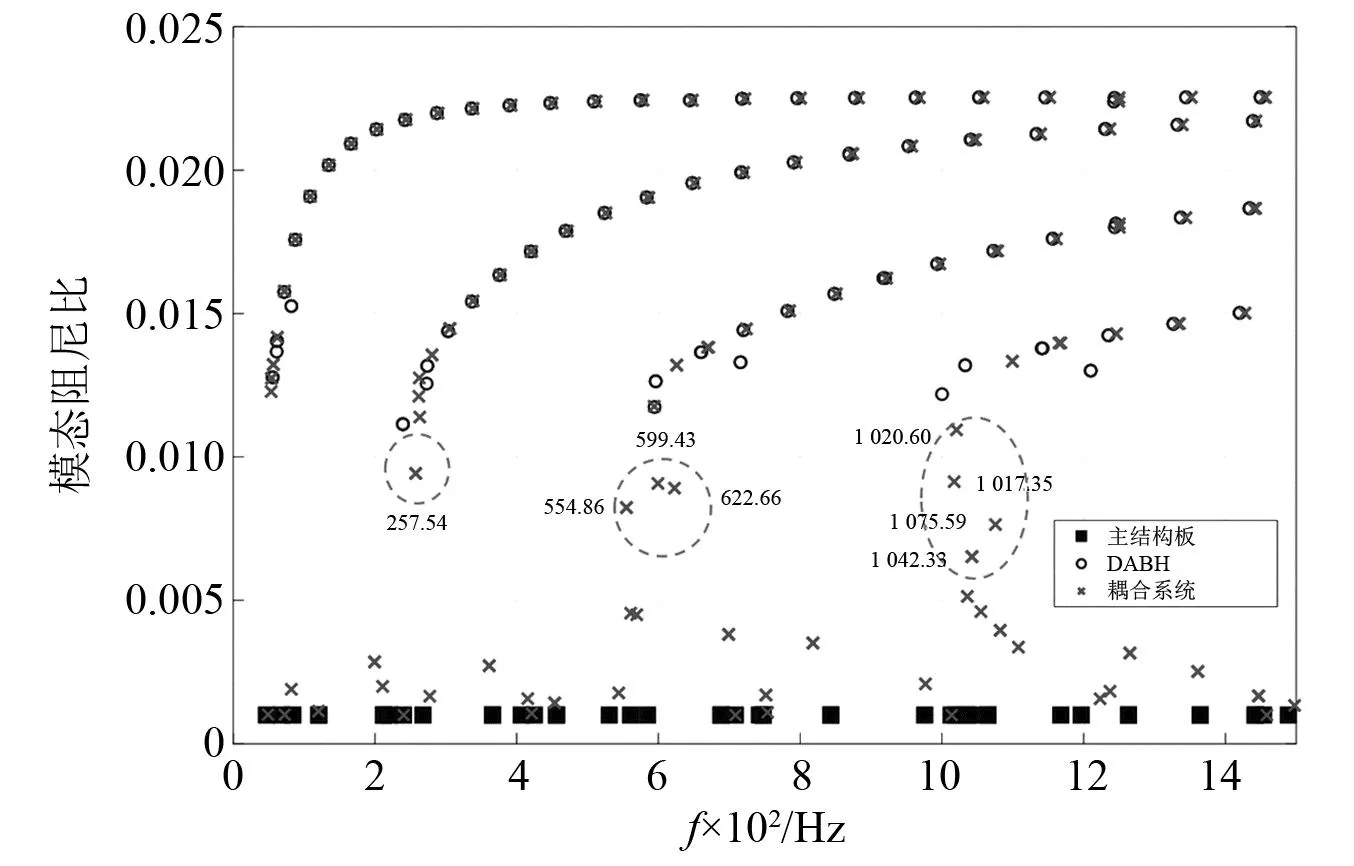
图15 耦合系统及其组成部分的模态阻尼比Fig.15 Modal damping ratios of coupled systems and different components

通过改变DABH结构参数,调整其模态频率,可实现对主结构板特定频率的减振。为了验证这一推论,改变DABH的固有频率,使之某阶固有频率与主结构板相近。为避免阻尼材料的干扰,假设阻尼材料损耗因子为0,仅通过改变阻尼的厚度来改变DABH的固有频率。当阻尼层厚度为3.3 mm, DABH第24阶固有频率为272.85 Hz,其振型为同心圆振型,如图16(b)所示,与主结构板的第11阶模态频率267.85 Hz相近。当阻尼层厚度为2.1 mm时,由于阻尼厚度的降低引起附加质量下降导致模态频率向高频移动,此时DABH的第3阶固有频率为66.67 Hz,其振型为同心圆振型,如图16(a)所示,与主结构的第2阶模态频率68.02 Hz相近,DABH的第33阶固有频率为371.03 Hz,其振型为非同心圆振型,如图16(c)所示,与主结构的第12阶模态频率366.04 Hz相近。图17(a)、图17(b)和图17(c)分别是66.67 Hz、272.85 Hz和371.03 Hz的强迫响应结果,可见,两个同心圆振型对应频率的峰值都发生了峰值分裂,展示了完美的DVA效应,而非同心圆振型对应的频率371.03 Hz,其峰值并未发生分裂。表明通过改变DABH结构参数,调整其模态频率,可实现对主结构板特定频率的减振。

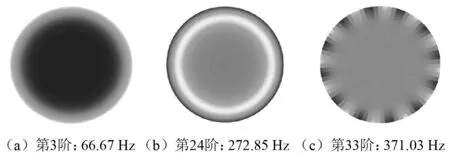
图16 DABH的模态振型Fig.16 Modal Shapes of DABH

图17 主结构板的振动响应MSVFig.17 MSV of the coupled structure

3 结 论

本文针对碟形声学黑洞与主结构板的耦合系统,在Rayleigh-Ritz法框架下,选择高斯函数作为基函数,建立了其半解析分析模型。研究了碟形声学黑洞结构参数以及连接位置对主结构板振动响应的影响规律,揭示了DABH宽频调谐减振机理。研究结论如下:

(1)利用Kirchhoff-Love薄板理论,考虑面内外位移,通过高斯基函数的选择、形函数筛选以及人工弹簧法,建立了基于高斯展开法的半解析模型。结果表明,半解析建模方法准确、高效,为机理分析和参数优化提供了计算手段。

(2)DABH具有优异的能量聚集效应。减少截断厚度、增大声学黑洞半径以及扩展延伸平台长度均能增强其ABH的能量聚集效应;在边缘尖端处粘贴阻尼材料以及将DABH安装在主结构板的振幅较大处,均可提升DABH对主结构板的减振作用。

(3)利用DABH丰富的模态,通过调整DABH的固有频率,可最大限度地实现DABH与主结构的模态耦合,使DABH起到完美的DVA调谐减振作用,有效降低主结构板某些特定频率的振动响应,达到宽频调谐减振的目的。