红砂岩粗粒土破碎性质及累积变形模型研究

龙 尧, 张同文, 李建平, 张家生, 肖源杰

(1. 湖南高速铁路职业技术学院 铁道工程学院,湖南 衡阳 421002; 2. 高铁及轨道交通智慧运维湖南省工程研究中心,湖南 衡阳 421002; 3. 中南大学 土木工程学院,长沙 410075)

路基土体的稳定影响着轨道整体平顺性和列车行驶的安全性,随着我国高铁建设的飞速发展,对路基土体沉降特性的相关研究需求日益增大。铁路路基的工后沉降主要由动力变形产生[1-2],尤其是在我国华南泛红砂岩地区,由于列车动力荷载的反复作用,铁路运营过程中红砂岩粗粒土路基会产生大量破碎,导致路基产生明显的工后沉降。研究红砂岩粗粒土在不同应力状态下的破碎特性及累积变形规律,对指导红砂岩粗粒土路基工程设计和施工能够提供一定的理论依据和工程应用基础。

路基土的累积变形受到较多因素影响,其中主要有动力作用次数、围压、动应力比、含水率以及颗粒破碎等内外因素。近几年来,不少学者针对动力作用下路基土的累积变形规律进行了研究,所构建的累积变形模型主要分为显式模型和隐式模型。尽管具有明确物理意义的隐式模型计算精度相较更高,但为了满足精度要求,大多数隐式模型需要采用足够小的步长来模拟每个装载和卸载循环的过程,容易导致模型因过度计算而失效,计算难度较高。相比隐式模型,显式模型基于试验或现场规律建立,模型参数主要由试验或现场数据拟合获取,尽管其通常不具备明确的物理意义,但显式模型所需参数较少且易于确定,因此工程应用广泛。Ren等[3]在对Monismith提出的指数模型与Hardin-Drnevich本构模型进行类比分析的基础上,提出了一种新的三参数累积应变显式模型,该模型考虑了动态偏应力、循环荷载施加次数、土壤物理状态的影响。Zhang等[4]通过长期循环(10 000次循环)三轴试验,研究了含水量、循环荷载次数、偏应力和围压对路基土累积永久应变演变的影响,在此基础上提出并验证了一种考虑了荷载循环次数、初始体积应力、八面体剪应力及饱和度的路基土累积变形显式模型。Lu等[5]对高液限红黏土开展了一系列的室内试验,确定了其物理和力学特性,考虑了动态偏应力、重复荷载次数和路基土材料特性的影响,建立了新的累积变形显式模型并通过数值计算进行了参数研究。王启云等[6]开展了高速列车荷载作用下的粗粒土累积变形试验研究,构建了包含降雨入渗量、加载频率以及动应力幅值参数的累积应变显式模型。Mei等[7]认为粗粒土的累积变形与动应力幅值、侧向应力状态有关,开展了粗粒土的动三轴试验,构建了含有加载次数、动力幅值以及围压参数的累积变形显式模型。石熊[8]采用室内路基足尺模型试验系统对III型板式无咋轨道进行了循环荷载试验,研究了路基在高速列车动力荷载下的动力累积变形规律,提出了包含动静应力比、静应力与静强度比、振动次数为参数的指数型累积变形显式模型。周文权等[9]采用力学测试与模拟(mechanical testing and simulation,MTS)作动器研究了重载铁路粗粒土基床层的累积变形发展规律,构建了考虑围压、动应力幅值以及含水率的粗粒土累积应变预测显式模型,该模型适用于对动应力小于临界动应力的工况进行累积变形预测。谢栎等[10]针对红黏土的累积变形特性,采用GDS动三轴仪进行了排水条件下的循环荷载试验,得到了考虑循环应力比、固结应力及围压影响的红黏土累积变形显式模型。龙尧等[11]针对粗粒土开展了大型三轴试验,根据粗粒土的动力特性,构建了含有循环应力比和围压参数的累积变形显式模型。Chen等[12]针对粗粒残积土在最佳含水量条件下的变形行为进行了大规模单调三轴试验与长期循环三轴试验,考虑循环应力比(cyclic stress ratio,CSR)与围压的影响,分析了颗粒破碎行为对残积土变形的影响,建立了残积土路基交通荷载诱发变形的经验预测显式模型,该模型考虑了循环应力比、现场围压以及交通荷载的数量。

从上述研究中可以得出,目前,路基土的累积变形模型的研究主要采用显式模型,其模型参数较少且易于获取,能够更好地满足工程实践的需求,在实际工程中具有更广泛的应用。同时,当前针对红砂岩粗粒土累积变形的研究较少,尤其缺乏对其动力破碎特性的研究,并且考虑颗粒破碎的累积变形显式模型相关研究几乎没有。因此,在体现颗粒破碎行为影响的基础上,满足工程实践需求,高效、便捷的红砂岩粗粒土累积变形显式预测模型亟待提出。本文针对铁路红砂岩粗粒土路基的颗粒破碎性质,开展室内大型动三轴试验研究,构建考虑颗粒破碎的粗粒土累积变形显式模型,并对模型进行修正。

1 试样制备及试验方案

1.1 试验仪器及制样

本文采用室内大型静动三轴试验仪进行红砂岩粗粒土破碎试验,试样采自湘北长沙某工地,采用孔隙率制样[13],为了研究粒径大小对颗粒破碎的影响规律,本文取3种单一粒径粗粒土,分别为D1=45.0-31.5 mm,D2=25.0-16.0 mm以及D3=16.0-7.1 mm,制样过程如图1所示。本文材料参数、试验仪器与文献[14]一致。

图1 制样过程Fig.1 Sample preparation process

1.2 试验方法

为了保证列车安全行驶,铁路路基不容许发生破坏变形,填料应力状态大部分情况下为动力稳定状态。关于试验过程土体应力状态取值,根据2023年龙尧等的研究成果,本文列车荷载取频率3 Hz,动偏应力取100 kPa,静偏应力取20 kPa,荷载频率取3 Hz,围压为80 kPa,荷载作用次数分别取5 000次,10 000次,20 000次,30 000次,40 000以及50 000次,对每次作用后的粗粒土进行筛分。动力试验后的筛分过程如图2所示。

图2 筛分试验Fig.2 Sieve after dynamic test

根据文献[15]的研究结果,采用25个颗粒和100个颗粒所得到的形状系数统计平均值差别不大,说明在精度要求不是非常严格的条件下,选取颗粒数大于25个,即可组成代表性样品并以此来初步判定红砂岩粗粒土颗粒整体形状平均值。本文为了研究颗粒破碎过程中的形状演化规律,在动力试验过程中,每个试件中随机选取30颗红砂岩颗粒,每个颗粒进行染色并标号,置于试件上部1/3高度,颗粒形状试验如图3所示。

图3 颗粒形状试验Fig.3 Particle shape test

2 试验结果及分析

2.1 动弹性模量变化分析

在传统工程设计中,动弹性模量被作为一个恒定的刚度指标,而实际上即使在动力加载条件下,随着应变的逐渐增加,土的刚度也会表现出显著的非线性软化[16]。因此分析粗粒土的动弹性模量变形十分必要。对于大应变变形,即当动剪应变幅大于10-3时,Seed等[17]提出将动应力幅值和弹性应变的比值定义为土体的动弹性模量Mr,如式(1)

(1)

式中:σd为动应力幅值,kPa;εa为某一振次下的最大动应变,%;εp为对应卸载后的最小动应变,%;εr为动弹性应变,%。动力加载条件下,不同大小粒径对应的动弹性应变、动弹性模量与加载次数之间的关系,如图4和图5所示。

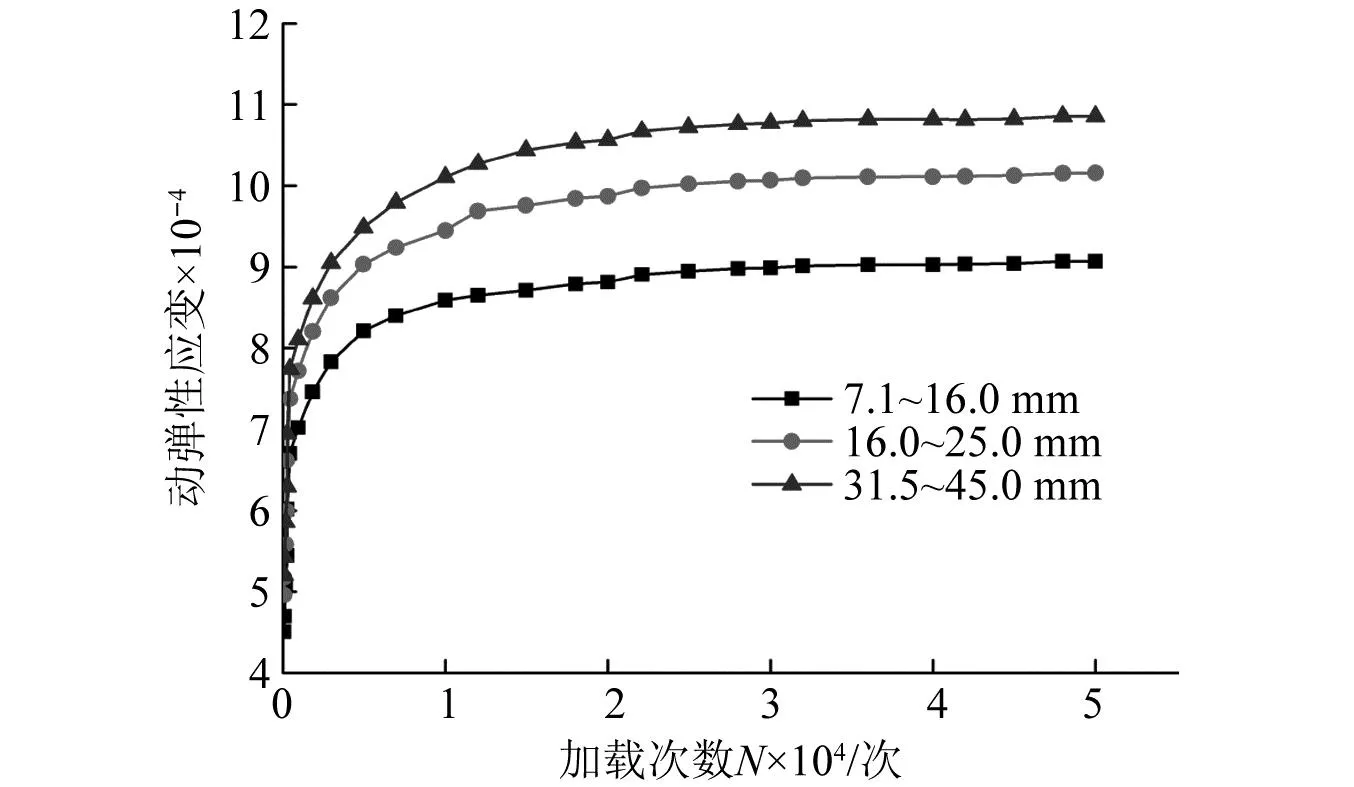
图4 动弹性应变随加载次数的变化趋势Fig.4 Variation trend of dynamic elastic strain with loading times

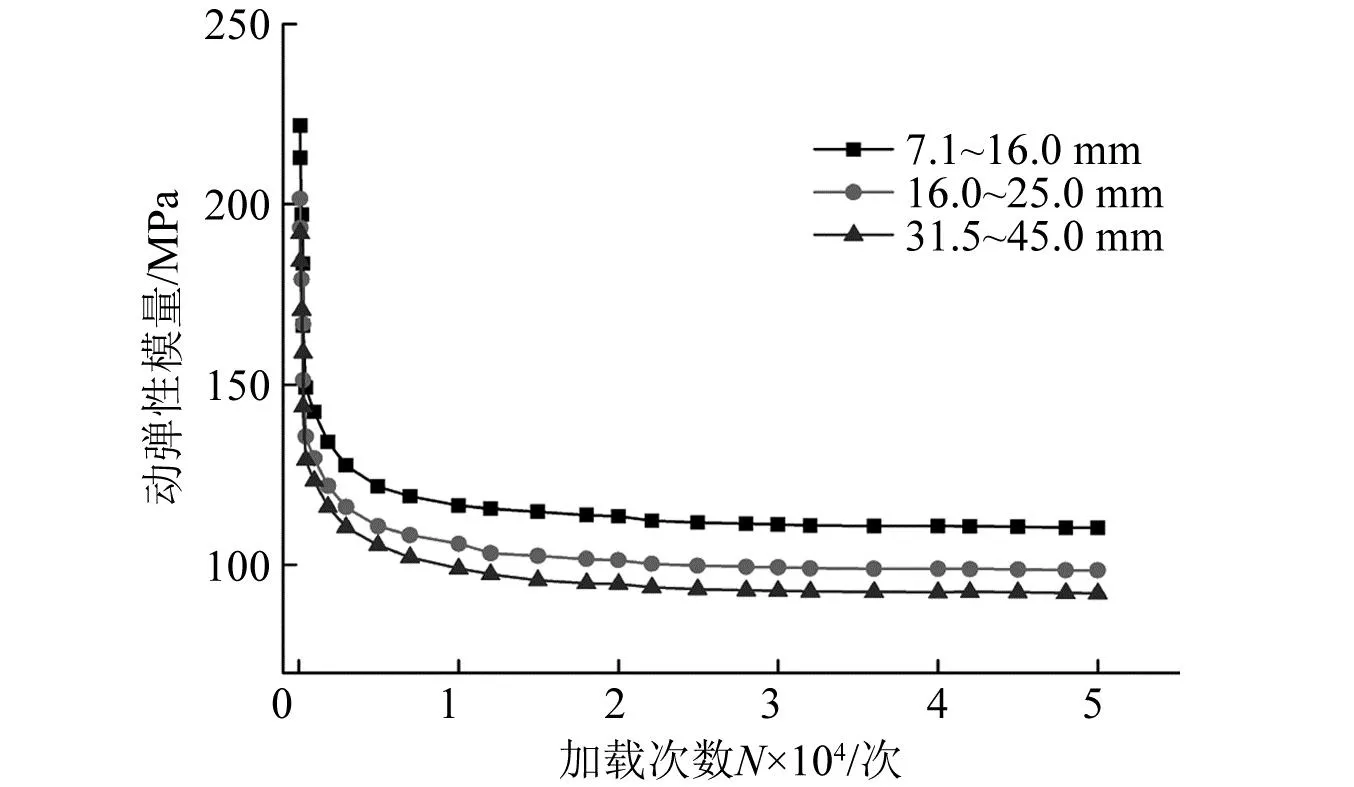
图5 动弹性模量与加载次数的关系Fig.5 The relationship between dynamic elastic modulus and loading times

不同粒径颗粒在相同外界应力水平下会产生不同的动弹性应变,图4揭示了粒径大小对粗粒土土体动弹性应变的影响。由图4可知,土体粒径越大,动弹性应变越大。这是因为红砂岩粗粒土粒径越大,颗粒破碎程度越显著,大粒径自身结构劣化越明显,大粒径试样变形越大,其回弹模量就较小,因此动幅值一定的条件下,颗粒粒径越大回弹应变越大。另外,随着加载次数的增大,不同粒径的动弹性应变先快速增大最后逐渐趋于稳定,说明土体强度在应变过程中不断增大并趋于某个定值。

从图5动弹性模量随着加载次数的增加不断减小,说明动力作用下粗粒土强度不断弱化,出现应变软化现象。在加载初期曲线减小幅度较大,超过20 000次以后动弹模逐渐趋于稳定,动应变基本完成。这也证明了土体强度随加载过程不断调整,最终趋于稳定。

2.2 颗粒破碎率与颗粒形状系数的关系

本文采用Marsal[18]提出的破碎率Br。通过动力三轴试验得到不同粒径颗粒加载次数与颗粒破碎率Br之间的关系如图6所示。

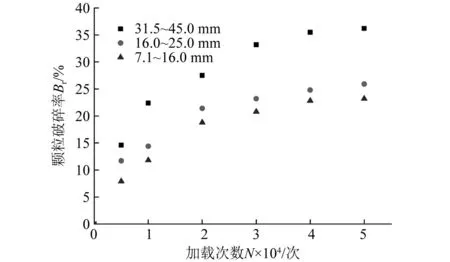
图6 颗粒破碎率Br与加载次数的关系曲线Fig.6 The relation curve of particle breakage rate Br and loading times

关于颗粒形状描述的系数较多,其中修正Blaschke系数[19]表示的是颗粒的外观轮廓与圆的接近程度。文中根据红砂岩实际的破碎情况以及计算的方便性,文中选择修正的Blaschke系数作为形状变化的度量,其计算方式为

(2)

式中:A为颗粒最大投影面积, mm2;p为颗粒最大投影边界长度之和,mm;Cb的取值范围为0～1,其值越趋近1说明形状越近似圆形。采用图像处理软件ImageJ对颗粒二维形状轮廓进行采集并分析,得出试验前、后每个颗粒形状修正Blaschke系数,通过前后差值除以试验前形状系数,得到形状系数变化率。加载次数与形状系数、形状系数变化率之间的关系如图7和图8所示。

图7 动力试验前后平均形状系数对比Fig.7 Comparison of mean shape coefficient before and after dynamic test

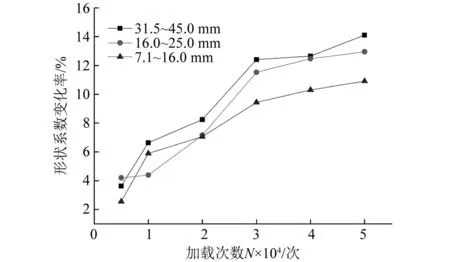
图8 加载次数与形状系数变化率的关系Fig.8 The relationship between loading times and the change rate of shape coefficient

由图7可知,不同粒径在试验后形状系数都会有所增加,增加幅度不同,系数值都趋近1,说明颗粒都是向圆形演变。此外,由图8可知,31.5～45.0 mm, 16.0～25.0 mm 和7.1～16.0 mm的颗粒形状系数变化趋势大致相同,在作用次数20 000次以前, 形状系数变化率增长较快;20 000次以后,形状系数变化率逐渐趋于稳定,与图6中颗粒破碎率的演化规律相类似。这是因为,形状系数的变化与颗粒破碎是息息相关的,颗粒破碎直接导致了颗粒形状的变化,而且颗粒在破碎过程有自适应性,即颗粒总是朝着不易破碎的形态转化。自然界的颗粒都有棱角,这些部位在外界荷载作用下容易产生应力集中现象,因此颗粒棱角在动力作用下会断裂并脱离母体,重新发展成一个新的颗粒体,并跟母体一样进行自适应变化。而圆形是相对较不容易破碎的一种形状,所以颗粒在破碎过程中会不断去棱角、研磨,朝着圆形去进化。在20 000次加载量之前,颗粒破碎程度较大,对应的形状变化也较大;加载20 000次之后,颗粒通过自适应调整,逐渐完成形状的调整,进化为不易破碎状态,即靠近或相似于球形,所以形状系数变化率增加量较小。

3 基于颗粒破碎的累积变形模型

Monismith等[20]在对路基变形进行研究时,认为累积动应变主要与荷载作用次数有关,其提出了两参数累积塑性变形,该模型在一定程度上表达了在循环荷载作用下的路基变形的趋势,该模型对处于失稳变形状态的路基有较好的预测性[21],但对于属于稳定状态的变形则描述性较差。Monismith提出的两参数模型如式(3)

εp=a×Nb

(3)

式中:εp为累积应变;N为加载次数;a,b为拟合参数,跟土的应力状态、类型和物理状态等因素有关。

土的应力状态是影响累计变形主要原因之一,Li等[22]引入了静强度参数并间接考虑土体类型及物理参数等,从半理论和半经验的角度分析了道路交通荷载作用下的土体累积变形,如式(4)

(4)

式中:qf为土体静强度,kPa;qd为动偏应力,kPa;a,b和c为拟合参数。而交通路基往往具有初始静荷载,即路面或者轨道板及轨道等。Chai等[23]进一步考虑初始静偏应力对土体永久变形的影响,如式(5)

(5)

式中:qs为初始静偏应力;a,b,c,d为拟合参数。

Hornych等[24]认为土体的累积变形分为两个部分:前100次由于荷载动力压密或是加载装置与土体接触不紧密引起的残余变形;100次以后为动力荷载作用下的累积变形,如式(6)

(6)

式中:εp1(100)为N=100次时的轴向累积变形;A和B为拟合系数,且B>0。由式(5)可得式(7)

(7)

从式(7)中可以得出,当N→+∞,A=εp(N)-εp1(100),即A值为最大累积应变减去前100次加载时的应变。

有文献[25]指出动偏应力qd、静偏应力qs、静强度qf对土的累积变形影响很大。动偏应力和静偏应力属于土的应力状态范围,静强度和颗粒破碎则属于物理状态。如果将颗粒破碎引入描述累积变形模型中,则能够更客观反映破碎状态演化过程,揭示颗粒破碎对粗颗粒土累积变形的影响机理。

从上述可知,系数A的主要影响因素为应力状态(qd,qs)和物理状态(qf,Br),用下述函数表示为

A=f1(qd/qf)·f2(qs/qf)·f3(Br)

(8)

参考孔祥辉等的研究,f1如式(9)

(9)

Chai等的研究表明f2如式(10)

f2(qs/qf)=1+qs/qf

(10)

观察式(7),当N越大,等式右侧越趋近于A值。所以当文中动三轴试验加载次数超过5 000次时,式(7)可以近似认为

A=εp(N)-ε100(N)

(11)

结合图6数据,可得到颗粒破碎与轴向累积应变A的关系,如图9所示。

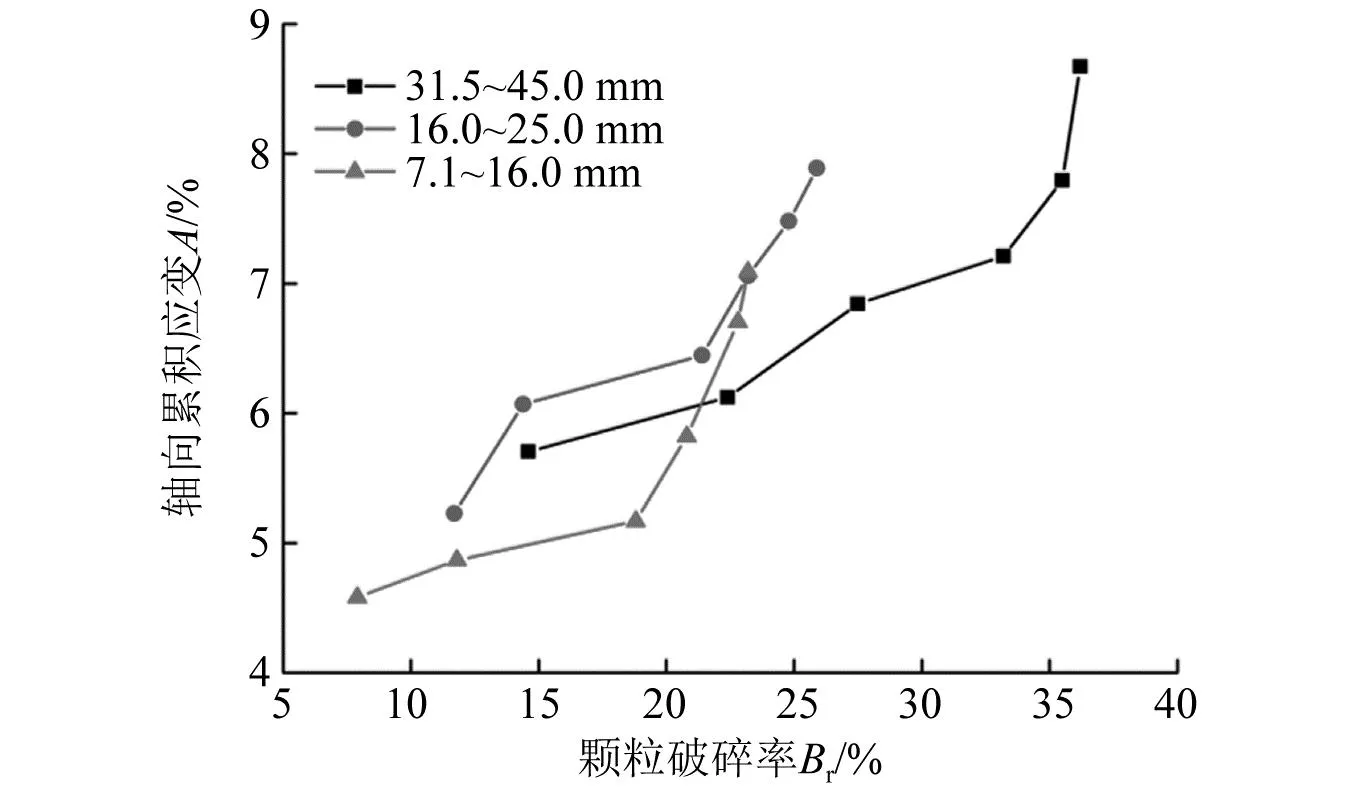
图9 颗粒破碎Br与轴向累积应变A的关系Fig.9 Relationship between particle breakage rate Br and axial accumulated strain A

从图9中可以看出颗粒破碎Br与轴向累积应变A的关系曲线形式,采用幂函数形式描述两者关系如式(12)

(12)

式中:a1,b1和c1为破碎拟合参数;Br为颗粒破碎率,%。采用式(12)对图9中数据进行拟合,可以得到不同粒径的拟合参数值,如表1所示。

表1 颗粒破碎与累积应变拟合参数Tab.1 Particle breakage and cumulative strain fitting parameters

对比式(12)和式(8),两式具有相容性,可以得到式(13)

A=a2·f3(Br)

(13)

结合式(7)～式(13),可以得到式(14)

(14)

在铁路荷载数以千万计的往复荷载作用下,前一百次的应变相对总应变是非常小。因此可以得到式(15)

εp(N)-εp1(100)≈εp(N)

(15)

由式(14)和式(15),可得式(16)

(16)

从式(16)中可以看出,考虑颗粒破碎的累计变形模型包括应力参数、物理参数以及拟合参数。其中qd和qs为设计参数,根据现场实际应力状态确定;qf和Br为物理状态参数,分别通过静三轴试验和级配筛分试验确定;a,b,c,d,f和g为拟合参数,通过试验数据拟合得到。参数类型及确定方式归纳如表2所示。

4 模型应用、修正及适用条件

4.1 累积应变模型的应用

对动三轴试验数据进行拟合计算,得到试验数据和拟合曲线的关系,如图10所示。从图10中可以看出,计算出来的拟合曲线与试验数据拟合度较好,拟合曲线反映了试验数据的曲线形态,前期加速变形和后期稳定变形阶段的形态描述准确,对其轴向累积应变发展全过程有较好的描述。拟合反算得到参数a,b,c,d,f和g,列入表3中。

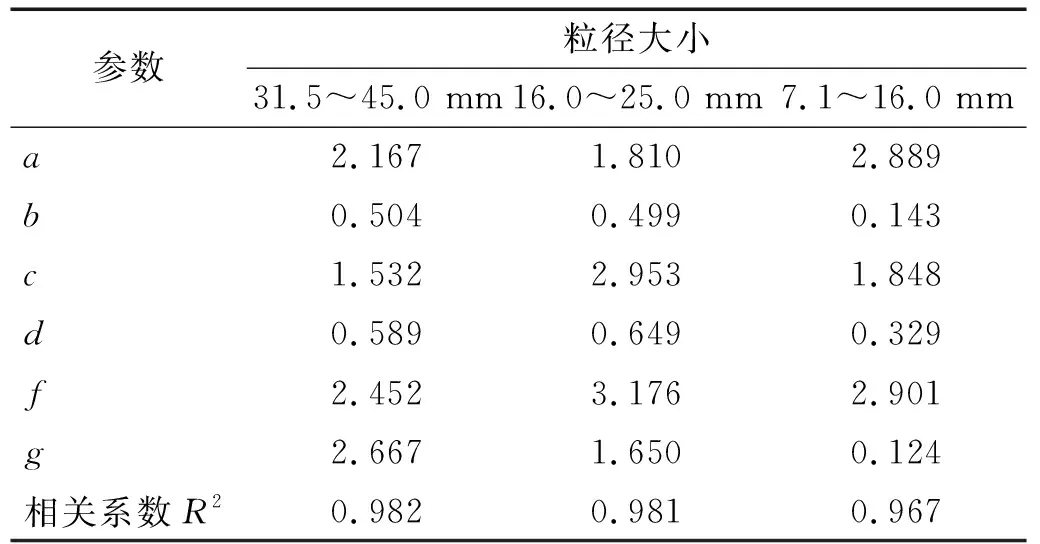
表3 累积变形拟合参数Tab.3 Cumulative deformation fitting parameter

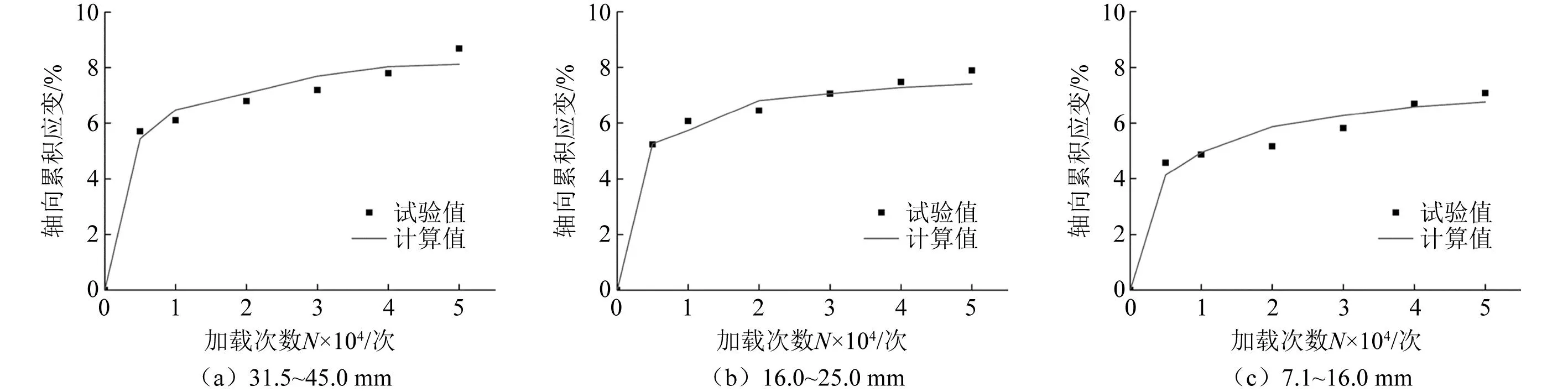
图10 不同粒径的加载次数与轴向累积应变的关系Fig.10 Relationship between loading times and axial cumulative strain with different particle size

4.2 累积应变模型修正

从参数表3可以看出,不同粒径大小同一参数值变化不大,为了方便参数的选取,增加工程适用性,对拟合参数采用拟合平均值对模型进行验算,参数选取如表4所示。累积变形模型初步拟合曲线如图11所示。

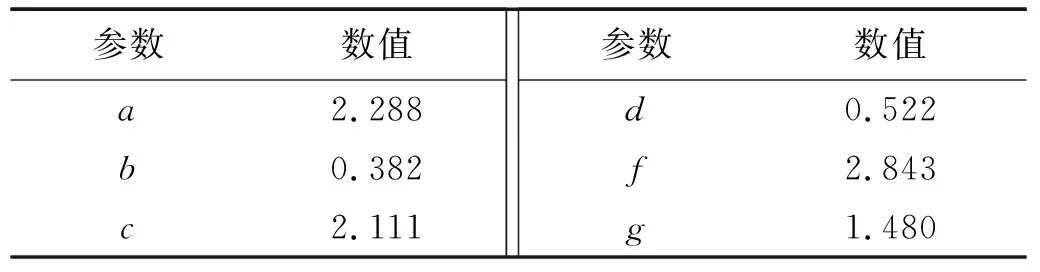
表4 累积应变模型参数选取Tab.4 Parameter selection of cumulative strain model

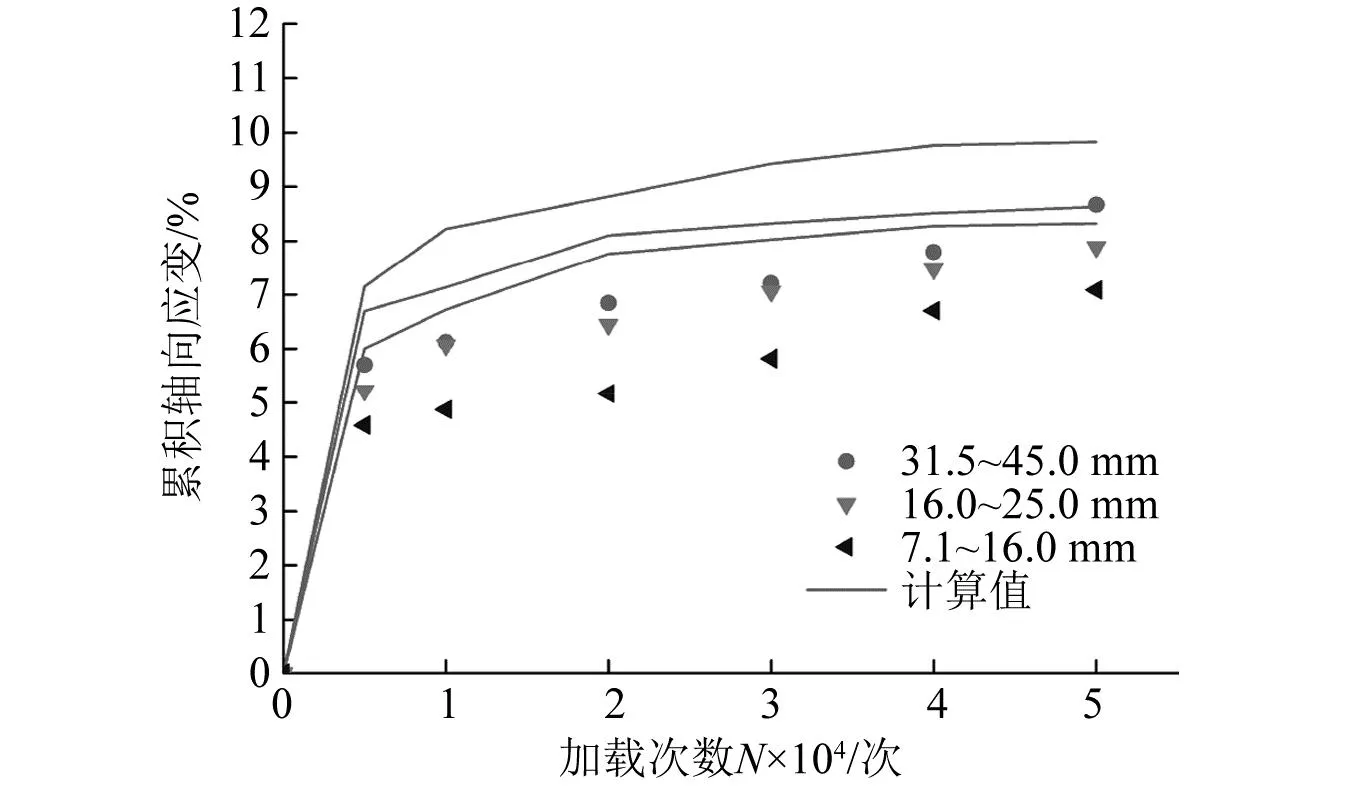
图11 累积变形模型初步拟合曲线Fig.11 Preliminary fitting curve of cumulative deformation model

从图11中可知,初步拟合曲线能够表达轴向累积变形的变化趋势,但是式(16)的计算数据偏差较大,对比计算数据和试验数据,计算值普遍大于试验值,因此需要对模型进行修正。分析图中计算曲线与试验曲线,试验数据约为计算数据的0.8倍。因此,引入修正系数ψ=0.8,由式(16)可得式(17)

(17)

采用修正累积变形模型式(17)并代入表4模型参数,对试验数据进行计算,可得计算曲线与试验曲线之间的关系,如图12所示。由图12可知,修正后的累积变形模型能够较好地预测红砂岩颗粒土在破碎条件下的前期加速阶段和后期稳定变形阶段动力轴向累积变形,31.5～45.0 mm和16.0～25.0 mm的粒径对应的计算曲线拟合度较高,虽然7.1～16.0 mm粒径计算曲线精确度有待提高,但是整体上预测了其累积变形趋势,总体计算精度明显提高。

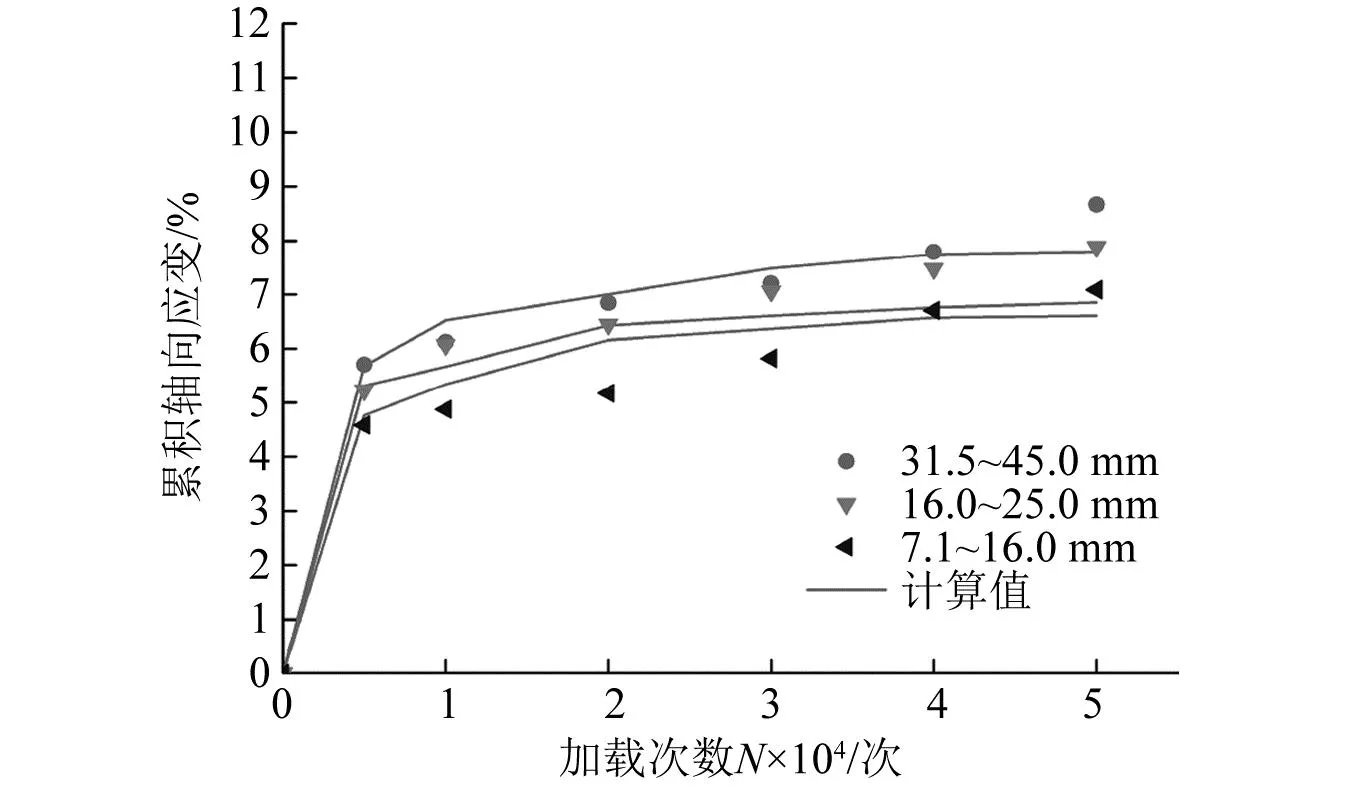
图12 修正后的累积变形模型计算曲线Fig.12 The calculation curve of the modified cumulative deformation model

为了分析颗粒破碎率对轴向累积应变的影响,文中采用式(17)计算模型,选取了加载次数20 000次时,单一分析颗粒破碎量增长条件下的累积应变变化趋势,如图13所示。由图13可知,当颗粒破碎率为0时,累积应变约为3%。这时累积应变主要是动力导致的剪缩作用产生,粗粒土颗粒该阶段主要体积变形,并没有破碎效应的影响。随着累计变形的发展,体积变形不足以消耗外界做功,这时颗粒破碎现象出现。随着颗粒破碎率的不断增加,累积应变也不断增加。基本上颗粒破碎出现后,累积应变与颗粒破碎率基本呈线性关系。说明颗粒破碎对累积变形的影响非常显著,颗粒破碎所产生的颗粒尺寸变化、土体结构重组、级配变化等结果最终都导致了土体的累积变形。

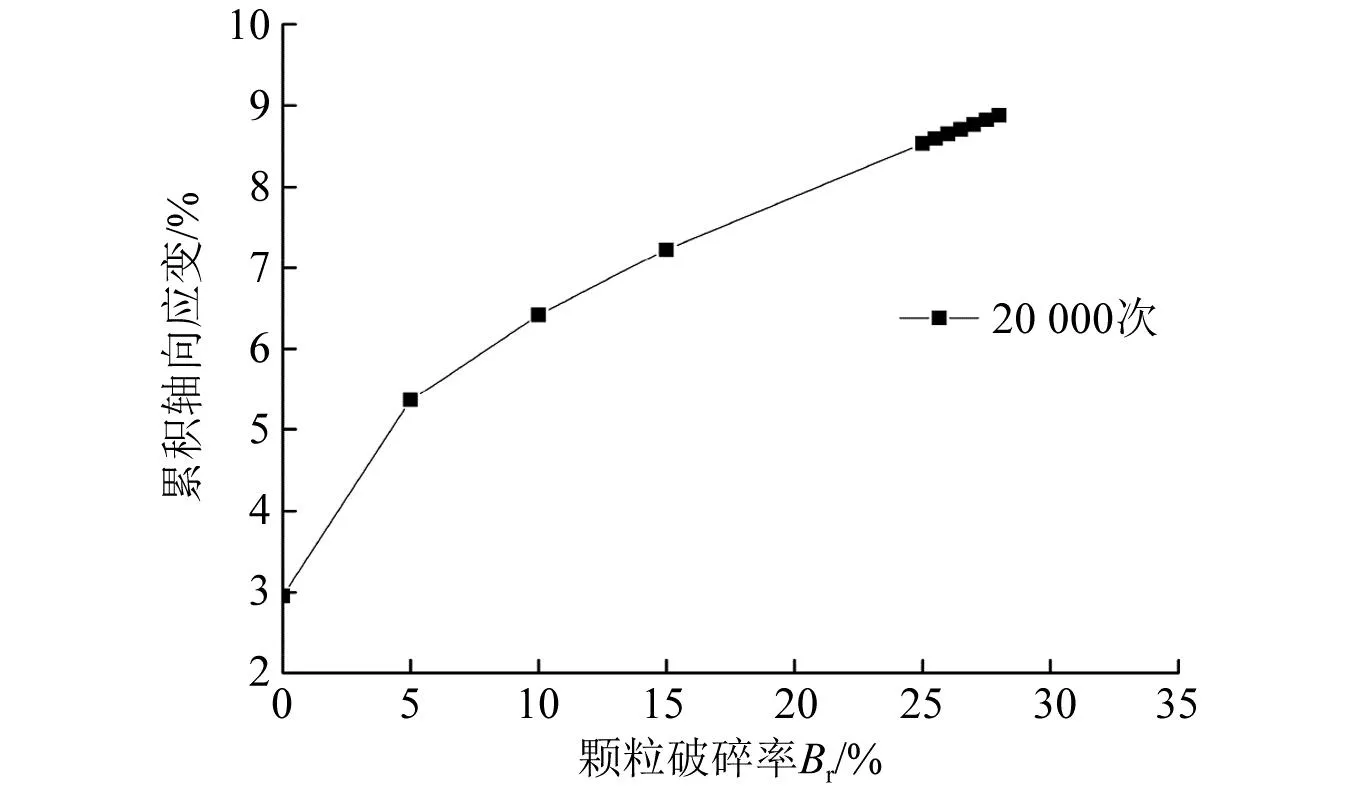
图13 颗粒破碎率与累积应变的关系Fig.13 Relationship between particle breakage rate and cumulative strain

4.3 模型适用条件分析

本模型的建立考虑了应力、物理状态以及拟合参数的影响,但本文仅对于稳定型累积变形具有较好的描述作用,未对破坏型累积变形曲线进行预测,因此有待于进一步研究失稳状态下的粗粒土累积变形研究。

此外,室内试验与工程实践现场的工况不可避免地存在差异,工程现场的累积变形受诸多因素影响,为提高模型对工程现场的预测精度,修正系数需要对比工程实践数据进行调整,以便对不同工况的累积变形进行精准描述。同时,由于本模型的参数较多,以及对于某粒径(工况)的拟合度需要提高,因此下一步研究工作需要将模型参数进一步简化,在修正系数和参数关系方面进行研究,提高工况普适性,增强工程适用性。

5 结 论

本文通过动力三轴试验研究了红砂岩的动力特性并得到了累计破碎变形模型。模型能够较好地描述破碎状态下的红砂岩粗粒土累积变形规律,具有较高的拟合度。拟合参数能够进行试验确定,使得模型具有较高的工程实践性,能对红砂岩粗粒土路基变形趋势的进行预测。主要结论如下:

(1) 粒径越大,动弹性应变越显著,动回弹模量越小。修正Blaschke形状系数变化率与颗粒破碎率的演化规律基本相同,颗粒破碎导致了颗粒形状变化,随着动荷载不断作用,形状系数接近于1,颗粒越趋于圆形。

(2) 根据红砂岩粗粒土路基的动力变形特性,构建了考虑颗粒破碎的累积变形模型。该模型为半理论半经验模型,其参数包含了应力状态参数、物理状态参数和拟合参数三种。

(3) 所构建的考虑颗粒破碎的累积变形模型能够较好地描述红砂岩粗粒土路基的动力累积变形趋势,对累积变形曲线的加速变形和稳定变形都有较好的预测。同时,对累积变形模型拟合参数进行了确定,便于在实际工程应用中计算红砂岩粗粒土路基变形时参数的选取,为考虑颗粒破碎的累积变形模型提供了预测基础。

(4) 对于模型预测值与试验值之间的精度问题,文中对该模型进行了修正,加入了修正系数ψ,使得该模型能更好预测红砂岩粗粒土的累积变形过程。此外,在特定作用次数下,颗粒破碎对累积应变的单一影响是非常显著的,颗粒破碎量与累积应变之间基本呈线性关系。