基于联合仿真的飞机着陆机场跑道桥动载特性研究

孟宪锋, 赵星燕, 江 辉, 吴松华, 曹铁志, 罗 萌, 孙永学

(1. 民航机场规划设计研究总院有限公司,北京 100029; 2. 民航机场工程技术研究中心,北京 100029; 3. 北京交通大学 土木建筑工程学院,北京 100044)

我国民用机场存在旺盛的建设需求,也面临一系列现实的建设障碍。一方面,既有公路、铁路网及河流等对大型枢纽机场的扩建形成限制;另一方面,山区、滨海等区域进行机场建设时,存在地貌限制、建设用地不足等问题。跑道桥的应用可以解决机场建设面临的地形限制,是解决上述问题的有效方案。

目前,滑行道桥在国内外应用较为广泛,跑道桥在国外也已有少数工程应用,如葡萄牙罗纳尔多国际机场、美国亚特兰大机场等,但我国跑道桥建设目前仍处于空白阶段。随着我国机场建设范围的不断扩展,跑道桥的规划设计引起了广泛关注。对于跑道桥的推广应用,飞机动载作用下桥梁的动力响应及其影响规律是面临的首要问题。

当前,各国学者对滑行道桥动力响应特性的研究已有一定开展。孙荣梅[1]通过数值模拟、理论分析与现场实测,分析了滑行道桥位移冲击系数与桥面平整度、飞机滑行速度等影响因素之间的关系,建立了滑行道桥冲击系数计算模型。张宇辉等[2]通过数值模拟和现场实测分析了滑行道桥的动力响应规律,研究表明桥梁动力响应在飞机主起落架通过跨中时达到最大值。孙荣梅等[3]以首都机场5号滑行道桥为研究对象,采用理论分析和现场实测的方法分析了机-桥耦合系统的振动特征。Moulds[4]通过对已建成的滑行道桥进行大量调研与分析,建议将滑行道桥冲击系数取为0.3。Qi等[5]通过数值模拟对截面形式相同、宽跨比不同的滑行道桥冲击系数展开研究,结果表明滑行道桥冲击系数随宽跨比的增大而增大。

在飞机着陆冲击作用下跑道桥的动力响应特性方面,相关研究非常薄弱,仅有罗昆升等[6]通过数值模拟分析了飞机在公路桥梁上着陆对桥梁动力响应的影响,研究发现飞机对着陆跨的作用最大,且桥梁下表面混凝土会出现局部开裂的现象。此外,国外不同机场对于跑道桥动力系数的取值各不相同,葡萄牙罗纳尔多国际机场分别将频遇、罕遇、偶然作用下跑道桥的动力系数取为1.5,2.0,3.0,美国亚特兰大机场在进行第五跑道桥建设时将动力系数取为1.4[7]。Reis等[8]指出Boeing 747-400着陆时跑道桥动力系数可达1.8,飞行员着陆操作不当造成异常冲击作用时甚至高达4.0。Moulds通过对既有跑道桥进行分析指出,跑道桥承受的冲击作用较大,极有可能超过飞机自质量的100%,但考虑到缓冲系统减振及燃料消耗,建议将跑道桥动力系数取为1.6。

在规范标准方面,我国JTG D60—2015《公路桥涵设计通用规范》[9]规定公路桥梁冲击系数是关于桥梁基频的函数,其范围在0.05～0.45;我国TB 10002—2017《铁路桥涵设计规范》[10]规定铁路桥梁动力系数取值与桥梁跨度相关。目前尚未有规范对机场桥梁的动力系数取值做出明确规定,且飞机着陆于跑道桥瞬间的直接冲击作用在作用机理上显著不同于车辆车轮与路面或钢轨之间动态接触作用的放大效应。而且,既有研究给出的跑道桥冲击系数建议取值相差较大,难以应用于我国跑道桥的建设。综上所述,有必要对该类桥梁的动力响应进行专门研究。

为研究飞机着陆滑跑过程中机场桥梁的动载特性,本文分别在多体动力学仿真软件与有限元软件中建立了精细的飞机模型和桥梁模型,两者联合实现机-桥耦合模型的建立,模拟了飞机在桥梁上着陆滑跑的全过程,分析了飞机着陆参数对桥梁动力响应的影响,给出了动力系数的主要分布范围,可供我国民航机场跑道桥的设计及相关规范修编参考。

1 机-桥耦合模型建立及验证

国内外关于飞机着陆桥梁动力过程模拟的研究十分薄弱。罗昆升等建立了简化的三自由度飞机模型,运用有限元软件LS-DYNA分析了飞机在预应力公路桥梁上着陆对桥梁动力响应的影响。但以上简化的三自由度飞机模型往往忽略了飞机缓冲系统的非线性特征,并且无法准确考虑飞机着陆姿态对桥梁动力响应的影响。

近些年来,基于有限元软件与多体动力学软件的联合仿真建模方法得到了学者们的青睐,该方法可通过动力学仿真软件建立精细的车辆模型和飞机模型,解决了以往研究中无法考虑车辆和飞机非线性特征及准确模拟飞机着陆姿态的不足。但该方法目前主要应用于车-桥耦合[11-16],为精确考虑飞机与桥梁之间的相互作用,本文首次将其应用于机-桥耦合模型的建立。联合仿真的一般流程如图1所示。

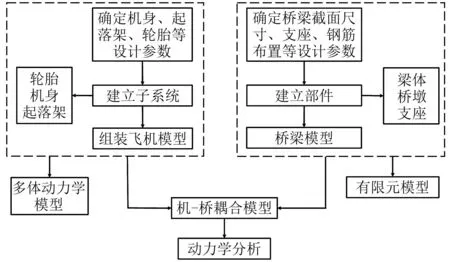
图1 联合仿真流程图Fig.1 Flowchart of co-simulation

1.1 桥梁模型

以某拟供C类飞机使用的机场跑道桥为研究对象,桥梁结构形式为预应力混凝土连续梁桥,跨径组合为(21+3×30+21)m,上部结构采用单箱15室箱梁,梁高2 m,桥宽45 m,桥墩采用薄壁式墩,横桥向布置四墩八支座,支座类型为盆式橡胶支座,桥台为一字墙式。其中,主梁采用C50混凝土,桥墩和桥台采用C40混凝土,预应力钢束采用高强度低松弛7股捻制预应力钢绞线,标准强度为1 860 MPa,桥梁立面图和横断面图分别如图2～图3所示。为方便下文叙述,假定主梁从左往右依次为第一跨、…、第五跨。

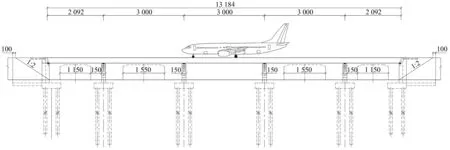
图2 桥梁立面图(cm)Fig.2 Elevation view of the bridge (cm)

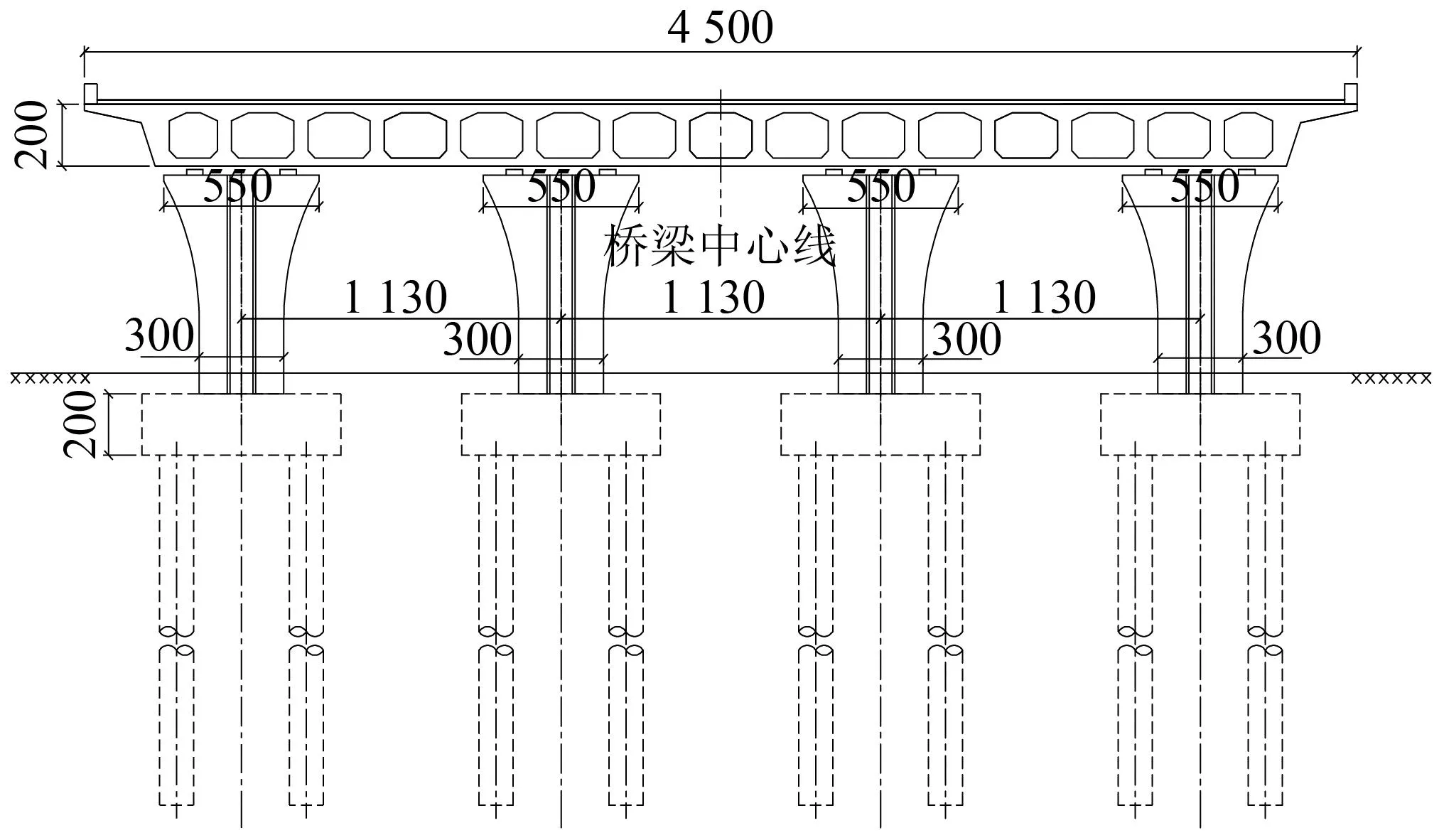
图3 桥梁横断面图(cm)Fig.3 Cross-sectional view of the bridge (cm)

本文基于ABAQUS有限元软件建立桥梁有限元模型,全桥共计47 973个单元,66 266个节点,如图4所示。有限元模型中主梁、桥墩及桥台均采用Solid单元模拟,钢筋采用Truss单元模拟,主梁和支座以及桥墩和支座之间采用MPC beam连接,桥梁支座采用ABAQUS软件自带的Connector中的Bushing连接单元模拟,能够较好地模拟支座力学性能,桥墩墩底采用固结约束。

图4 桥梁有限元模型Fig.4 Finite element model of the bridge

采用MIDAS/Civil建立相同模型,两相对比验证所建模型的准确性。定义相对误差δ如下

(1)

式中,TABAQUS和TMIDAS分别为ABAQUS和MIDAS/Civil中所建桥梁模型的周期,两个模型的前5阶振型、周期及相对误差如表1所示。由结果得知,两个模型的前五阶振型完全一致,且周期相对误差均在10%以内,证明了ABAQUS所建桥梁模型的正确性。

表1 桥梁自振特性对比Tab.1 Comparison of natural vibration characteristics of the bridge

1.2 飞机模型

本文以Boeing 737-800为研究对象,该机型起落架构型为三点式,机身质量为41 413 kg,飞机着陆参数如表2所示。根据Boeing 737-800机身、起落架和轮胎等设计参数,采用ADAMS/VI-Aircraft软件建立飞机的机身子系统、起落架子系统和轮胎子系统数值模型,为考虑飞机气动力变化和缓冲系统的非线性特征,根据相关理论计算得到飞机气动力特性、空气弹簧力特性以及油液阻尼力特性和轮胎动力特性[17],并将其以属性文件的形式定义在已经建立的起落架缓冲支柱和轮胎中。最后组装各子系统建立全机仿真模型,如图5所示。

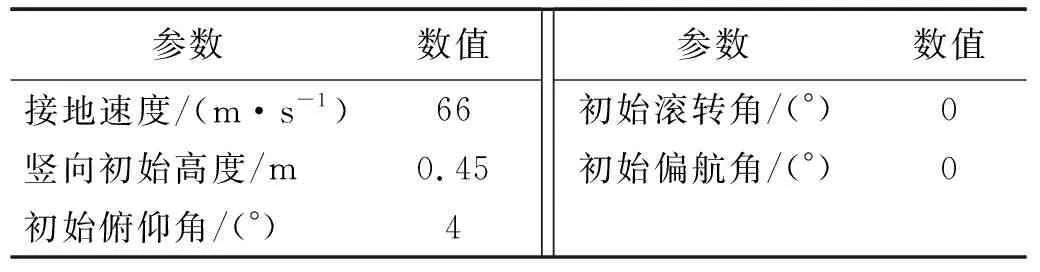
表2 飞机着陆状态参数Tab.2 The landing parameters of the aircraft

图5 Boeing 737-800飞机模型Fig.5 The aircraft model of Boeing 737-800

1.3 机-桥耦合模型

本文基于ADAMS/VI-Aircraft与ABAQUS的联合仿真分析流程如下:①基于SolidWorks建立桥梁三维几何模型;②采用ADAMS/VI-Aircraft建立桥梁多刚体模型;③对1.1节中建立的桥梁有限元模型进行模态分析和子结构分析,生成用于ADAMS/VI-Aircraft的柔性体模态中性文件;④使用柔性体替换桥梁刚体部件,建立ADAMS/VI-Aircraft中的桥梁柔性体模型;⑤组装飞机模型和桥梁模型,建立机-桥耦合模型。

建立机-桥耦合模型的关键在于准确模拟飞机着陆滑跑过程中与桥梁之间的相互作用,为此,本文通过在轮胎和桥梁间建立接触关系(如图6所示)进行约束,使飞机能以各种着陆姿态在桥梁上着陆滑跑,如图7所示。

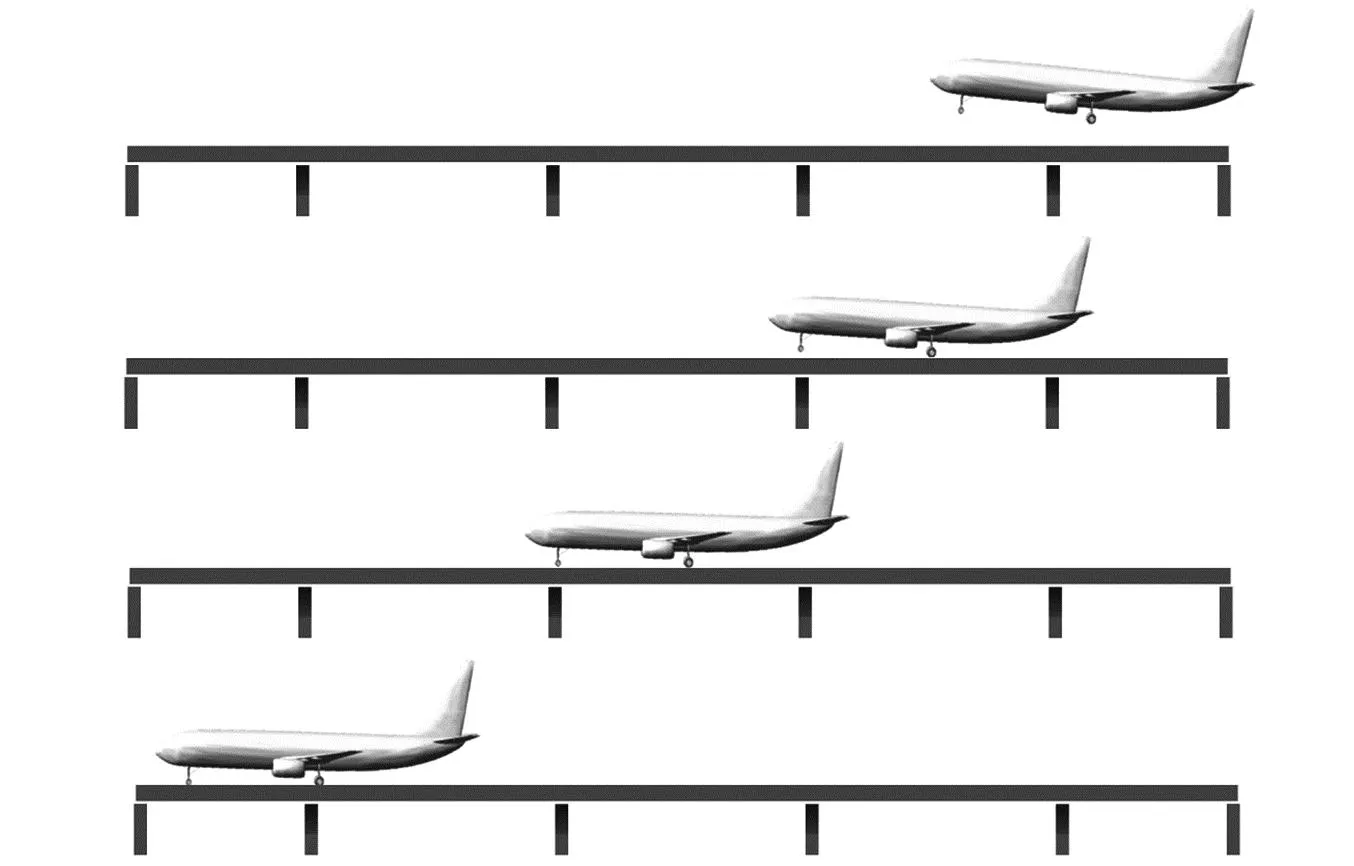
图7 飞机在桥梁的着陆滑跑全过程Fig.7 The whole process of aircraft landing and taxing on the bridge

1.4 机-桥耦合模型准确性验证

由于缺乏飞机着陆桥梁的实测数据,因此难以通过实测数据对比验证本文模拟方法的准确性。但飞机着陆机场道面的动力作用过程模拟可依靠ADAMS/VI-Aircraft软件独立完成,这是一种得到公认的成熟模拟方法[18-19],因此,本文通过对比同一飞机着陆刚性梁与着陆刚性道面的模拟结果来验证模拟方法的准确性。

如上所述,将柔性桥梁调整为刚性桥梁,采用1.3节中的方法建立飞机与刚性梁体间的接触,进行飞机着陆刚性梁体的模拟,如图8所示,并将前、后轮轮胎力计算结果与飞机着陆刚性道面(如图9所示)进行对比,结果如图10所示。

图8 飞机着陆刚性梁体Fig.8 Aircraft landing on a rigid beam body

图9 飞机着陆刚性道面Fig.9 Aircraft landing on a rigid runway

图10 轮胎力对比Fig.10 The comparison of tire force

由图10可知,两个模型的前轮轮胎力峰值分别为158.84 kN和163.37 kN,误差为2.77%,后轮轮胎力峰值分别为193.74 kN和194.04 kN,误差仅为0.16%,且轮胎力曲线较为接近,较好地验证了机-桥耦合模型的准确性。

2 分析工况设置

飞机着陆质量、接地速度、下沉速度、俯仰角、滚转角等主要着陆参数的取值范围可通过工程实际经验确定。其中,Boeing 737-800的着陆质量根据载客量、货运量以及运输距离的远近在空机质量41 413 kg与最大着陆质量66 361 kg之间变化[20]。飞机接地速度主要受着陆质量和风速影响,约为66 m/s[21]。Boeing 737-800以最大着陆质量66 361 kg着陆时,最大限制下沉速度为3.05 m/s[22]。飞行员在操纵飞机进行下滑着陆的时候,飞机处于“平飘”状态,俯仰角一般在3°～6°。

除此之外,飞机在着陆过程中受侧风影响时,难以保持稳定姿态,会出现各主起落架非同时着陆的现象,因此,分别对飞机以滚转角0°～4°着陆开展仿真分析。具体工况的参数及其取值如表3所示。

表3 不同工况参数及其取值Tab.3 Parameters and it’s values of different working condition

3 飞机着陆参数的影响

动力系数Df为飞机过桥时对桥梁结构产生的竖向动力效应的增大系数[23],可由式(2)表示

(2)

式中,Yd,max和Yj,max分别为飞机荷载对桥梁结构产生的竖向最大动、静响应,本文以桥梁结构的竖向位移计算动力系数,如图11所示。

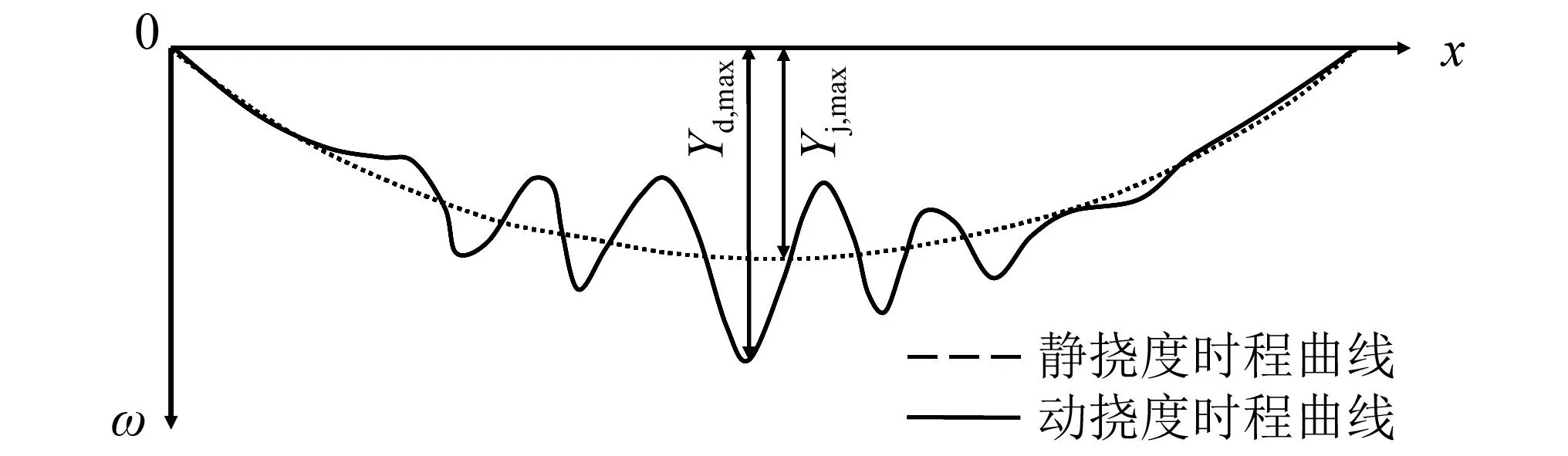
图11 Df计算示意图Fig.11 Schematic diagram of Df computing

3.1 着陆质量

为研究飞机着陆质量对桥梁动力响应的影响,在接地速度66 m/s、下沉速度2 m/s、俯仰角4°不变的情况下,分别计算了不同着陆质量下桥梁跨中竖向位移与Df。将飞机着陆点设置在桥梁第四跨,相应的飞机着陆时对第四跨冲击最大,因此仅列举该跨跨中的竖向位移时程曲线,计算结果如图12和图13所示。

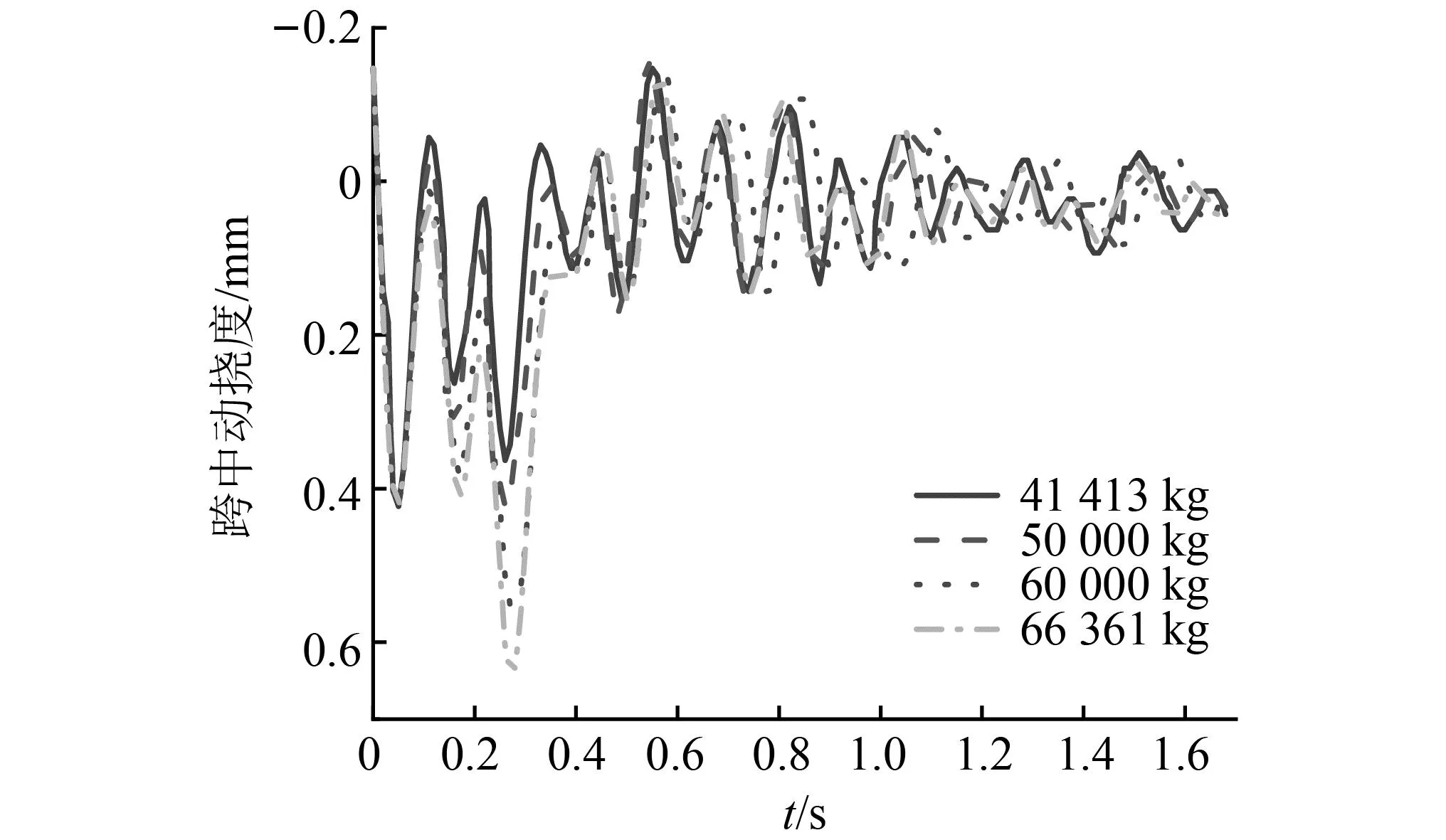
图12 第四跨跨中竖向位移时程曲线Fig.12 Time history curve of vertical displacement in the fourth span

图13 不同着陆质量下动力系数的分布Fig.13 The distribution of dynamic factor under different landing mass

由计算结果得知,飞机分别以空载、轻载、重载、满载着陆时,着陆跨跨中桥梁Df在1.16～1.48变化,且飞机着陆质量直接影响着陆冲击总能量,因此桥梁Df随着陆质量的增大而增大。与飞机着陆跨桥梁Df变化规律不同的是,第二、第三跨跨中桥梁Df随着陆质量的增大而减小,这是因为桥梁跨中竖向动、静位移均随着陆质量的增大而增大,但飞机运行至第二、第三跨时进入滑行阶段,此时飞机动载对桥梁的动力放大效应相较于着陆瞬间的冲击作用来讲大大降低,随着陆质量的增大,动挠度的增幅小于静挠度增幅,因此最终表现为第二、第三跨跨中桥梁Df随着陆质量的增大而减小,这一规律与车-桥耦合以及滑行阶段的机-桥耦合相同。

对比不同跨跨中桥梁Df的大小可以发现:第四跨跨中桥梁Df大于第二、第三跨,这是由于飞机着陆对第四跨冲击最大,随着飞机驶入第二、第三跨,飞机着陆状态稳定,对桥梁的作用力减小。此外,飞机着陆后的作用力在第四跨达到最大值后急剧下降,甚至小于静载下的作用力,因此第二、第三跨跨中桥梁Df<1,即动力响应小于静力响应,这也说明跑道桥设计时应分区考虑桥梁Df,以优化桥梁结构设计,减小经济投入。飞机接地速度、下沉速度、滚转角、俯仰角等参数也可得出相同结论,后续分析中不再做多余赘述。

3.2 接地速度

运行中飞机的受力不同于一般车辆,飞机运行过程中垂直方向上受重力、升力和地面反力的作用,在理想平整度情况下,飞机机翼所受升力随飞机运行速度的加快而增大,相应的飞机对地面的作用力会越来越小,如图14所示,这种特性会影响飞机着陆时对桥面冲击力的变化。因此,为研究飞机接地速度对桥梁动力响应的影响,在飞机着陆质量66 361 kg、下沉速度2 m/s、俯仰角4°不变的情况下,分别计算了不同接地速度下桥梁跨中竖向位移与Df,计算结果如图15和图16所示。

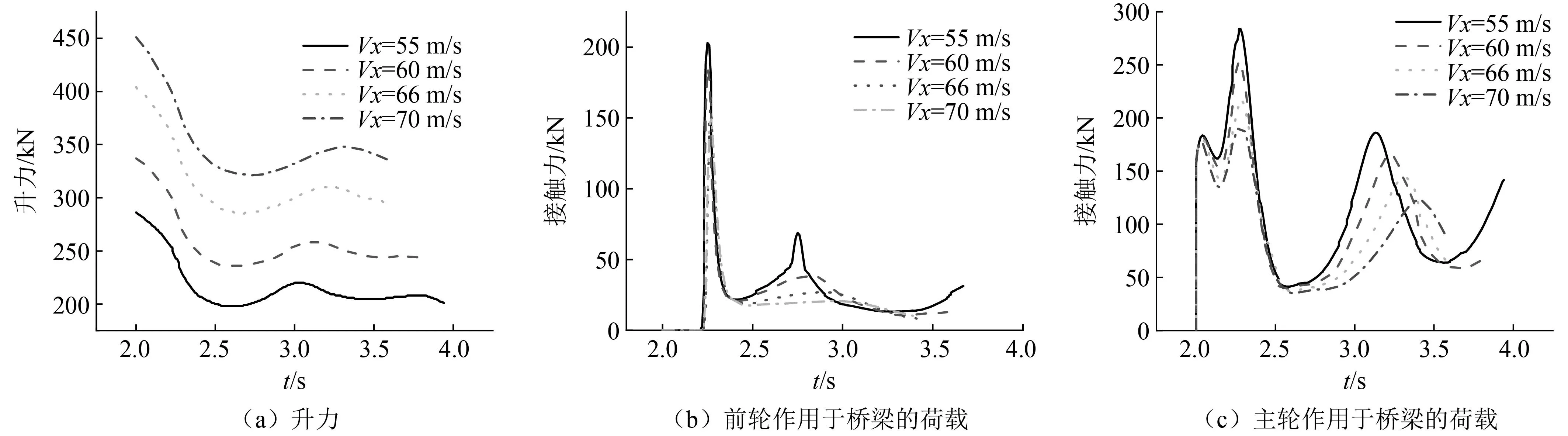
图14 不同接地速度下飞机升力及作用于桥梁的荷载变化曲线Fig.14 The load variation curves of lift and aircraft acting on the bridge under different grounding speed

图15 第四跨跨中竖向位移时程曲线Fig.15 Time history curve of vertical displacement in the fourth span

图16 不同接地速度下动力系数的分布Fig.16 The distribution of dynamic factor under different grounding speed

从计算结果可以看出,接地速度对桥梁Df的影响很大,飞机以接地速度55 m/s着陆时,着陆跨跨中桥梁Df为1.99,以接地速度70 m/s着陆时,桥梁Df为1.32,且由于飞机接地速度越大,飞机所受升力就越大,相应的对地面的作用力就越小,因此随着接地速度的增大,桥梁Df有降低的趋势,符合实际情况。

3.3 下沉速度

飞机着陆时的下沉速度受天气、气流、飞行员操纵技术等因素影响,离散型较大。因此,为研究下沉速度对桥梁动力响应的影响,在飞机着陆质量66 361 kg、接地速度66 m/s、俯仰角4°不变的情况下,分别计算了不同下沉速度下桥梁跨中竖向位移与Df,计算结果如图17和图18所示。

图17 第四跨跨中竖向位移时程曲线Fig.17 Time history curve of vertical displacement in the fourth span

图18 不同下沉速度下动力系数的分布Fig.18 The distribution of dynamic factor under different sinking speed

由图17和图18分析可得,桥梁Df受下沉速度影响很大,飞机以1.00～3.05 m/s的下沉速度着陆时,着陆跨跨中桥梁Df在0.98～1.87变化,增幅为90%,且由于下沉速度越大,飞机着陆冲击能量越大,因此随飞机下沉速度的增大,桥梁Df明显增大。

3.4 俯仰角

飞机在俯仰角1°～8°内着陆时,飞机俯仰角、升力及作用于桥梁的荷载变化曲线如图19所示,由结果可知,飞机升力随时间的变化趋势和机身俯仰角类似,升力随俯仰角的增大而增大,因此着陆瞬间主轮作用于桥梁的荷载峰值呈现逐渐减小的趋势。但飞机着陆俯仰角越大,前轮接地时刻越晚,俯仰力矩越大,因此前轮作用于桥梁的荷载峰值呈现逐渐增大的趋势。

图19 不同俯仰角下飞机俯仰角、升力及作用于桥梁的荷载变化曲线Fig.19 The variation curves of aircraft pitch angle, lift and load acting on the bridge under different pitch angle

为考虑飞机以不同俯仰角着陆对桥梁动力响应的影响,在飞机着陆质量66 361 kg、接地速度66 m/s、下沉速度2 m/s不变的情况下,分别计算了飞机以不同的俯仰角着陆时桥梁跨中竖向位移与Df,计算结果如图20和图21所示。

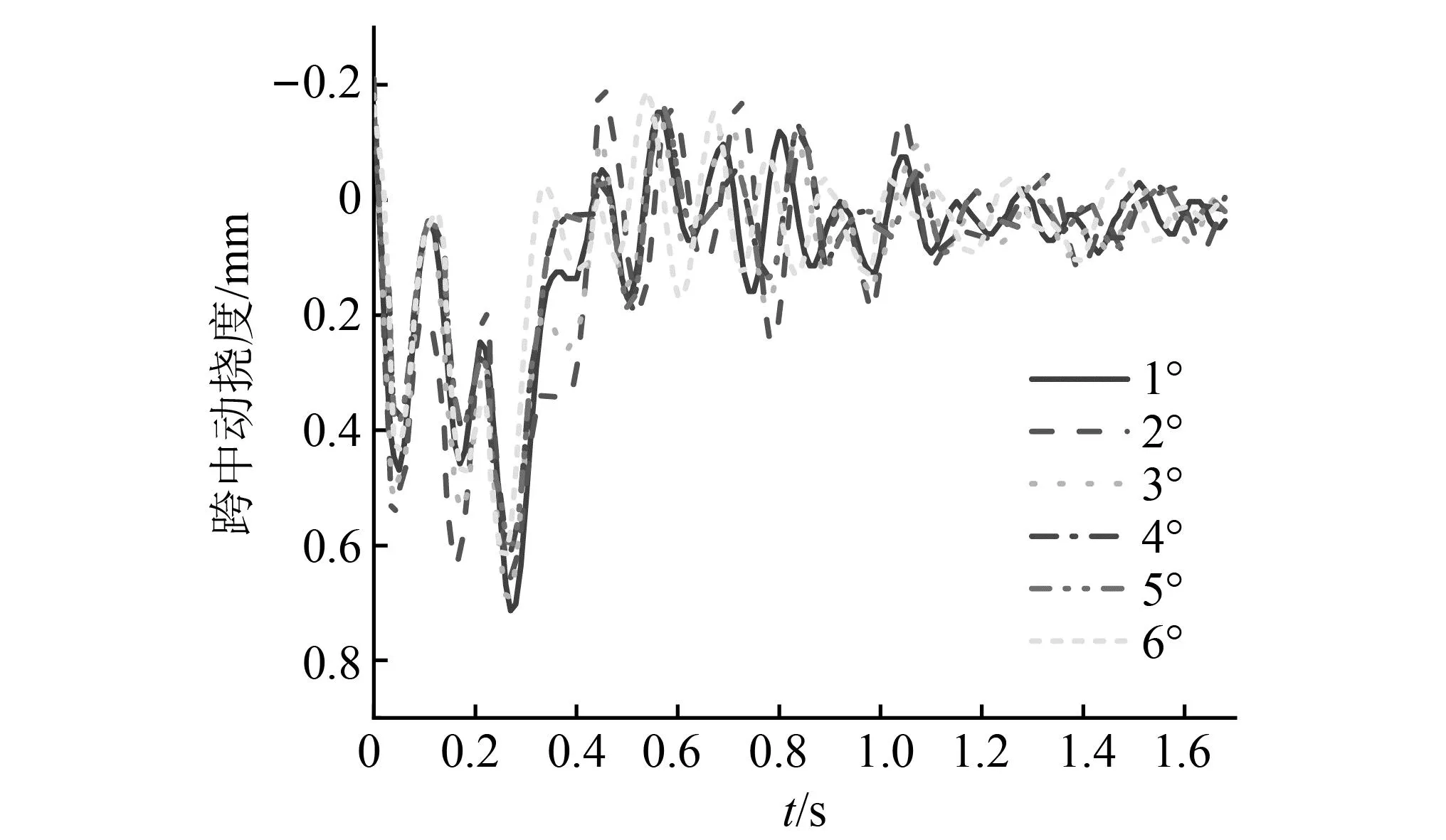
图20 第四跨跨中竖向位移时程曲线Fig.20 Time history curve of vertical displacement in the fourth span

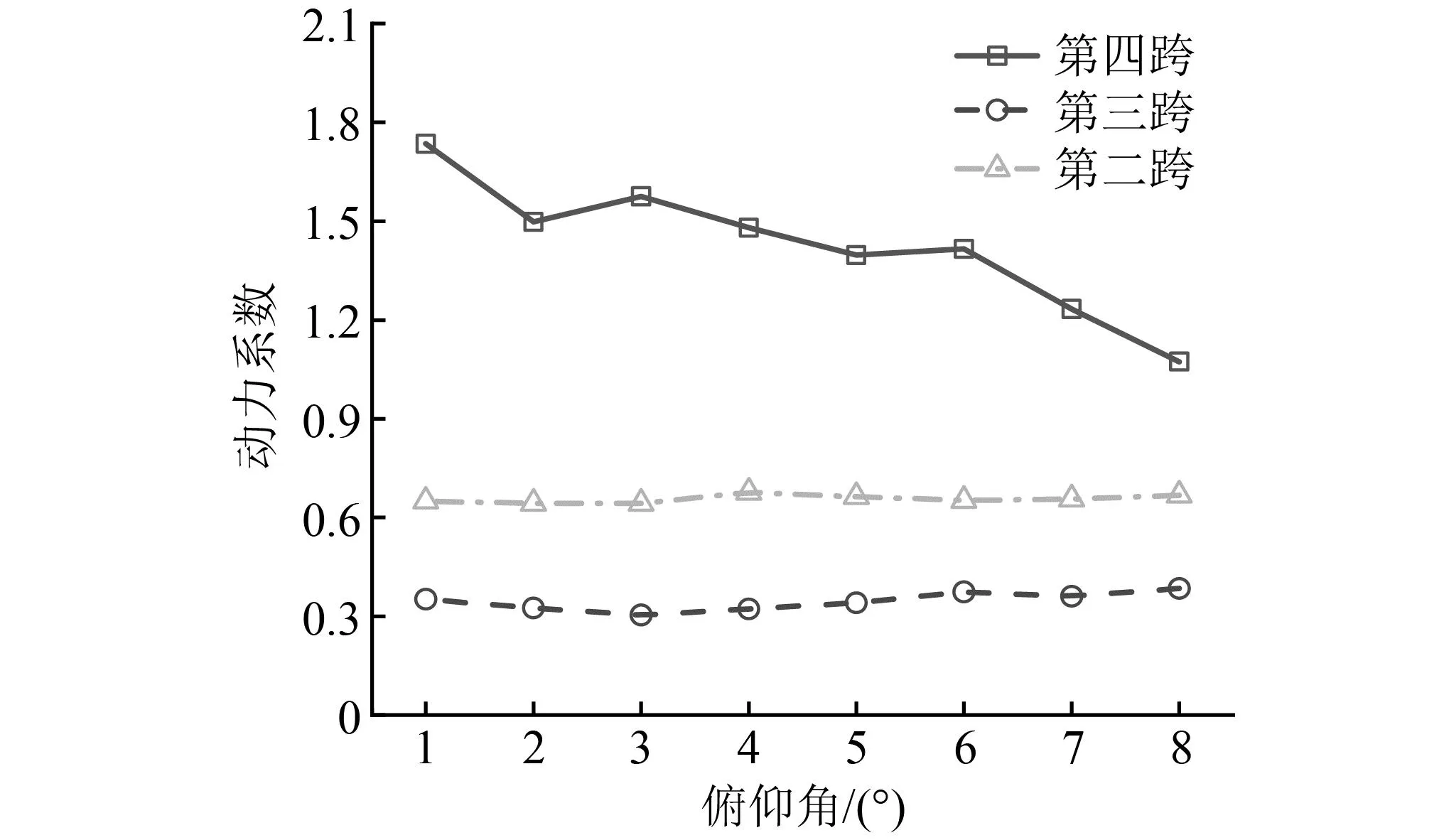
图21 不同俯仰角下动力系数的分布Fig.21 The distribution of dynamic factor under different pitch angle

计算结果表明,飞机以俯仰角1°～8°着陆时,着陆跨跨中桥梁Df在1.07～1.74变化,且以1°俯仰角着陆时,第四跨跨中桥梁Df为1.74,以8°俯仰角着陆时,桥梁Df为1.07,增幅为38%,随着俯仰角的增大,桥梁Df总体呈现减小的趋势。

3.5 滚转角

飞机以一定滚转角着陆时,右侧主起落架外侧轮胎(R4)先于其他主轮胎着陆,如图22所示。为研究飞机受侧风影响时非对称着陆对桥梁动力响应的影响,在飞机着陆质量66 361 kg、接地速度66 m/s、下沉速度2 m/s、俯仰角为4°不变的情况下,分别计算了飞机以不同滚转角着陆时桥梁跨中竖向位移与Df,计算结果如图23和图24所示。

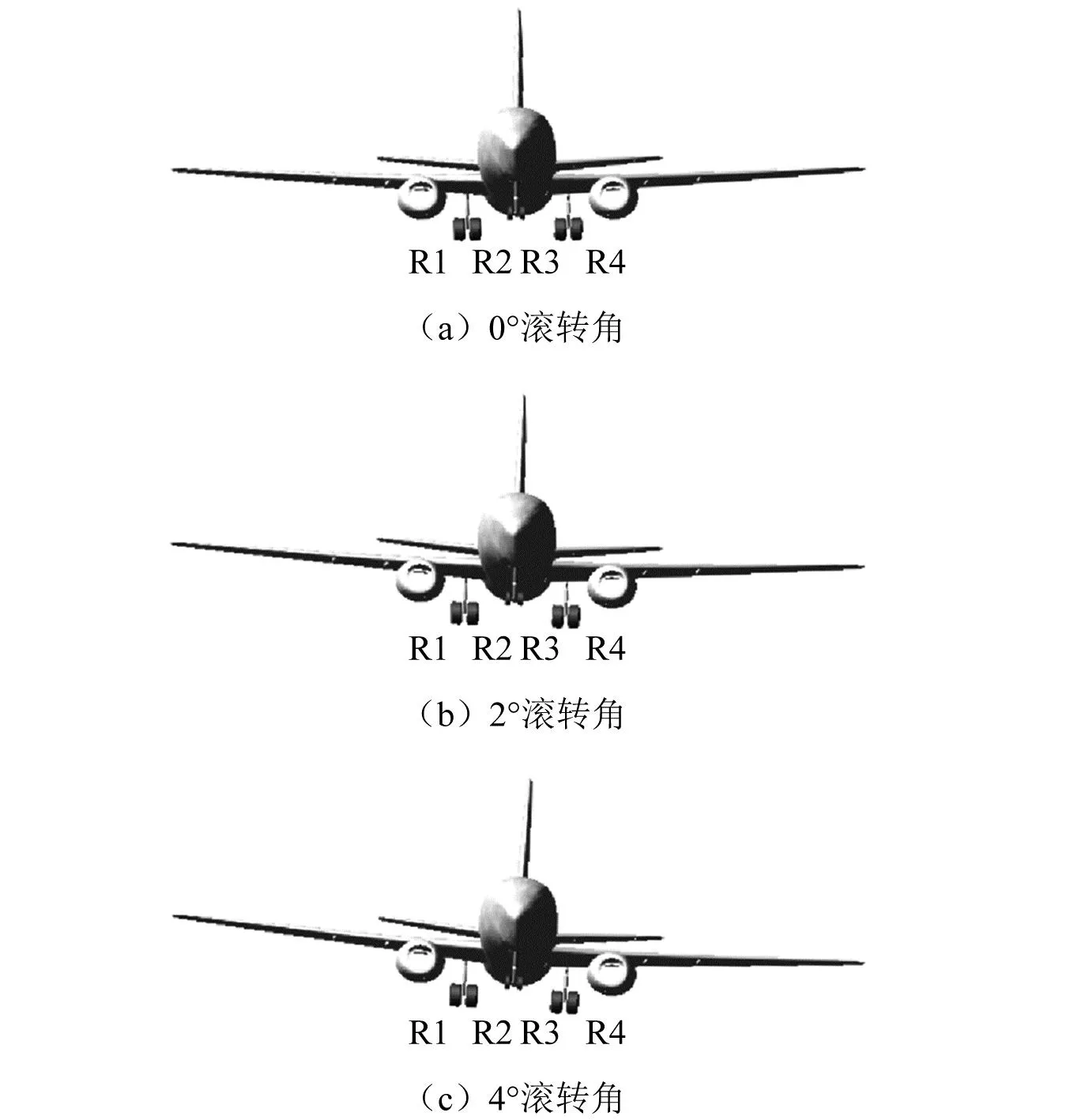
图22 飞机以不同滚转角着陆示意图Fig.22 Schematic diagram of aircraft landing at different roll angle

图23 第四跨跨中竖向位移时程曲线Fig.23 Time history curve of vertical displacement in the fourth span

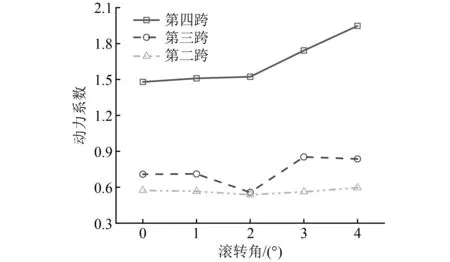
图24 不同滚转角下动力系数的分布Fig.24 The distribution of dynamic factor under different roll angle

由图23和图24可知,飞机着陆于桥梁时,滚转角的存在使得桥梁第四跨跨中竖向位移和Df相较于飞机对称着陆时明显增大,飞机以0°滚转角对称着陆时,桥梁Df为1.48,以4°滚转角非对称着陆时,桥梁Df为1.95,增幅为32%。除此之外,随着滚转角的增大,桥梁Df有增大的趋势,这是由于随滚转角增大,一侧主起落架外侧轮胎将承受更大着陆荷载,产生冲击力也将更大。

4 参数敏感性分析

为分析飞机不同着陆参数对桥梁Df影响程度的大小,定义Df相对差ξ,如式(3),该参数可反映桥梁Df在某工况下的离散程度,Df,max,Df,min分别为桥梁Df最大、最小值。不同着陆参数影响下,桥梁Df的数据分析结果如表4所示。

表4 计算结果数据分析Tab.4 Data analysis of calculation results

(3)

由表4可知,相较于着陆质量来讲,接地速度、下沉速度、俯仰角、滚转角的变化会对桥梁结构造成更大的冲击力,桥梁Df最高可达1.99。接地速度影响下桥梁Df的中位数为1.62,这表明有半数工况的桥梁Df在1.62以上,其余参数也可得出同样的结论。对比不同参数影响下桥梁Df的相对差可以发现,桥梁Df对五个着陆参数的敏感程度大小为:下沉速度>俯仰角>接地速度>滚转角>着陆质量。

5 结 论

本文首次采用联合仿真技术建立了机-桥耦合模型,模拟了飞机在桥梁上着陆滑跑的全过程,验证了模拟方法的准确性,并分析了飞机不同着陆状态对桥梁动力响应的影响及其变化规律,明确了桥梁动力系数的分布范围及各着陆参数对动力系数的影响程度,主要结论如下:

(1) 利用联合仿真方法建立了飞机-刚性梁体耦合模型,并将其着陆过程中的轮胎力与飞机着陆刚性道面进行对比,两者的前轮、后轮轮胎力误差仅为2.77%和0.16%,验证了所采用模拟方法的准确性。该方法可综合考虑飞机的气动力变化、缓冲系统非线性特征及各种着陆姿态,有助于开展精细化地机-桥耦合振动分析。

(2) 飞机在桥上着陆时,由冲击作用引起的桥梁动力系数最高可达1.99,最小为0.98,主要分布区间为1.26～1.62。不同飞机着陆参数对桥梁动力系数的影响程度由大到小依次为:下沉速度、俯仰角、接地速度、滚转角、着陆质量。

(3) 飞机对称着陆时,随着陆质量、下沉速度的增大,着陆跨桥梁动力系数明显增大,但接地速度、俯仰角越大,动力系数越小。飞机非对称着陆时,滚转角的存在使得飞机着陆时对桥梁的冲击作用增强,且动力系数随着滚转角的增大而增大。

(4) 飞机着陆对着陆跨的冲击力最大,随着飞机进入滑跑阶段,对其他跨的作用力减小,因此应对飞机主要着陆区域进行适当加强,或进行跑道桥设计时沿桥梁纵向分区考虑动力系数。

需要说明的是,本文以某一确定桥梁为对象开展了着陆滑跑过程中冲击作用对桥梁动载特性的影响,鉴于桥梁刚度、结构形式等势必对桥梁动载特性存在影响,后续我们将拓展研究桥梁主要设计参数对动载特性的影响程度及其规律。