重载机车102型钩缓装置动态模拟方法与动力学性能研究

张志超, 吕凯凯, 储高峰, 齐红瑞, 汪方文

(1. 中国铁道科学研究院集团有限公司 机车车辆研究所,北京 100081;2. 中车大同电力机车有限公司 技术中心, 山西 大同 037038)

重载机车运行安全性对重载铁路运输具有重要意义,集中体现在机车及其钩缓装置在纵向压钩力作用下的稳定性和动力学特性[1-3]。重载列车在制动时,机车往往处于最大纵向冲动的作用断面,在大纵向压钩力作用下,重载机车及其钩缓装置需要具有足够的受压稳定性。一旦车钩发生失稳将产生大的横向偏角,导致原本沿车体中心线传递的纵向车钩力产生横向分力,这些分力不仅会通过机车悬挂系统传递至轮轨界面,恶化轮轨作用关系,而且反过来会进一步加剧车钩偏转行为[4-8]。此外,重载机车在通过小半径曲线或者12号道岔侧线时,往往需要控制电制力级位避免产生明显增大的压钩力,否则由线路本身引起的较大车钩偏转角和复杂轮轨横向作用,再叠加明显的车钩横向分力作用势必加剧轮轨作用关系,引发安全问题[9]。因此,十分有必要开展重载机车及其钩缓装置动力学性能相关研究工作。

我国重载机车目前主要装备以100型车钩为代表的扁销钩缓装置和以101型、102型车钩为代表的圆销钩缓装置。张志超等[10-14]针对扁销钩缓装置的受压稳定性已开展大量研究工作,建立了各具特色的考虑缓冲器非线性迟滞特性、钩尾摩擦面作用、钩尾止挡特性的动力学模型。圆销钩缓装置主要通过钩尾两侧的钩肩结构与前从板位置的支承块相接触来获得车钩偏转回复力矩,对于这一类钩缓装置的受压稳定性早期也有一定的研究工作。罗世辉等[15-16]最早建立了考虑车钩转角和钩肩特性的圆销车钩动力学模型,分析了机车制动工况下轮轴横向力过大问题。曲天威等[17]采用理论分析与动态仿真相结合的方法研究了曲线与直线工况下圆销车钩自由转角与机车结构参数的关系。近几年,随着HXD2机车技术提升研究的推进,国内科研院所又开展了针对101型、102型圆销钩缓装置受压稳定性及其与机车悬挂参数匹配关系的研究工作,中国铁道科学研究院集团有限公司[18]在中车大同公司厂内试车线开展了HXD2机车与102型钩缓装置的受压稳定性试验,结果表明被试机车在直线线路上承受1 800 kN纵向压钩力时能够保证安全运行。然而,长期以来圆销钩缓装置钩肩止挡特性的模拟都是采用关联车钩偏转角与缓冲器压力的数学函数,未能充分考虑缓冲器的偏压特性,难以准确模拟钩肩与复原块相抵之后的动态响应特征,在系统受压动态响应的准确模拟、车钩自由转角与机车悬挂参数合理匹配、道岔与曲线线路上系统动力学特性分析等方面仍然存在不足。鉴于此,本文在前期研究工作基础上,通过加权等效离散方法将橡胶缓冲器简化为具有相同迟滞特性的多个阻抗力元,提出了能够准确模拟钩肩止挡和缓冲器偏压特性的102型钩缓装置动力学建模方法,进而采用子结构方法建立了双机牵引单元万吨列车编组的可靠动力学模型,计算分析了线路条件、机车与车钩关键结构参数等对重载机车及其钩缓装置动力学响应和运行安全性的影响规律,为重载机车102型钩缓装置的精细化模拟和技术提升研究提供了技术支撑。

1 102型钩缓装置及动力学建模方法

1.1 102型钩缓装置结构特点

102型圆销钩缓装置主要装备于HXN3、HXN5系列内燃机车以及技术提升HXD2型电力机车,其结构如图1(a)所示。该钩缓装置主要由钩头、车钩、钩尾框、钩尾圆销、对中复原装置(钩肩+支承块)、前从板、橡胶缓冲器等组成。纵向压钩力作用下,车钩绕其钩尾圆销可在一定范围内自由水平偏转,当车钩偏转至钩尾单侧钩肩与支承块相抵时,钩肩支承力会促使前从板偏压缓冲器,产生阻止车钩进一步偏转的阻力矩。通过调节挡肩和钩尾肩之间的间隙,可以改变车钩自由角以适应不同运用需求,如图1(b)所示。

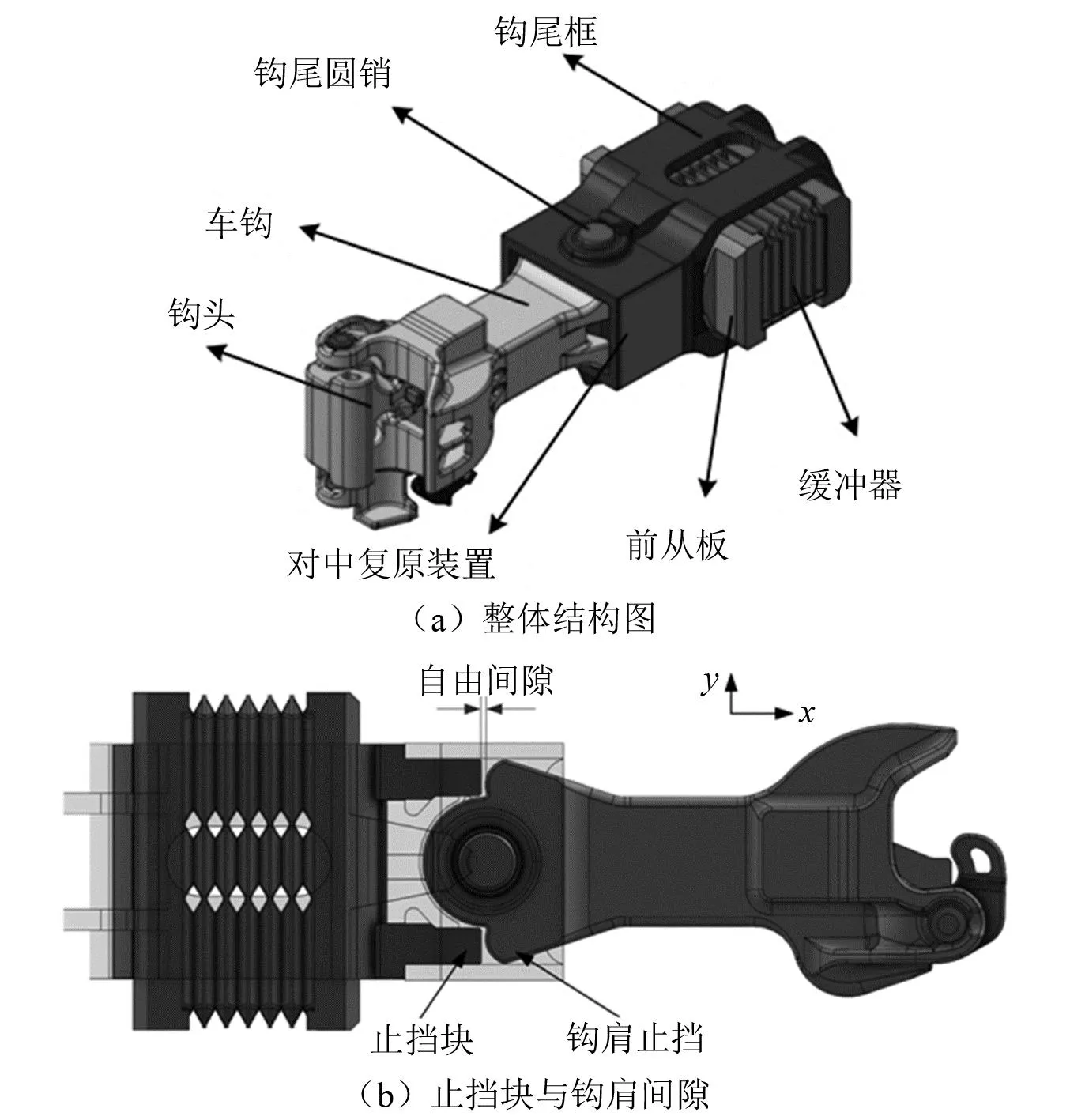
图1 102型车钩缓冲器结构图Fig.1 Structural chart of 102-type coupler and draft gear

在102型钩缓装置中,缓冲装置采用大刚度特性的NC390缓冲器,该缓冲器不仅需要缓冲重载列车间的纵向冲动,而且当车钩水平偏转至自由角后,还需通过偏压作用提供复原力,故最大阻抗力增加至4 500 kN,行程约42 mm,缓冲器容量约41 kJ,如图2(a)所示。作为对比,100型钩缓装置采用QKX100型车钩缓冲器,其特性曲线如图2(b)所示,由于13A车钩的旋转阻抗力矩靠钩尾弧面的摩擦力提供,采用大容量缓冲器可有效衰减摩擦弧面间的冲击,提高摩擦副的稳定,该缓冲器可提供的最大阻抗力为2 500 kN,最大行程为83 mm,容量大于100 kJ。

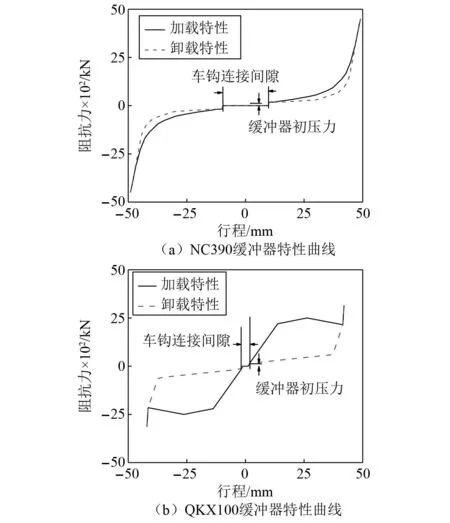
图2 缓冲器特性曲线对比Fig.2 Characteristic curves of different draft gear

1.2 102型钩缓装置数值模拟方法

由102型钩缓装置结构特点分析可知,钩肩与支承块相抵后通过前从板偏压缓冲器是影响圆销车钩受压稳定性的主要因素,准确模拟缓冲器的偏压特性便成为此类钩缓装置受压稳定性分析的关键问题。由于所用NC390缓冲器的橡胶材料特性和几何特性都呈复杂的非线性,其准确的非线性阻抗特性曲线难以通过理论计算或数值模拟方法获取。目前此类缓冲器的正压阻抗特性曲线主要通过静压、落锤试验方法获取,而其偏压特性的试验与研究较少,缺乏理论研究基础和试验数据支撑。在这样的条件下,本文将橡胶缓冲器离散为具有相同迟滞特性的阻抗力元,并引入剪切刚度用于考虑离散力元之间的剪切效应,建立了能够模拟缓冲器偏压特性的102型圆销钩缓装置动力学模型,其离散阻抗力元间的剪切刚度通过仿真结果与试验数据的对比修正获得。

首先,将橡胶缓冲器沿y轴方向(横向)进行离散来模拟其偏压特性,具体的离散力元数量通过解析法和离散法的对比来确定。分别采用解析法和离散法推导缓冲器的偏压刚度,通过比较不同离散力元数量所得偏压刚度与解析法的误差来确定其合理取值。缓冲器具有复杂的非线性迟滞阻抗特性,但这里为了便于缓冲器偏压刚度的推导求解,做出如下假设与定义:①缓冲器在纵向压缩量x时的刚度K(x)定义为缓冲器阻抗力对dx的微分dF(x);②假设缓冲器受压面均匀承载,且受压面内不同位置的刚度不因偏压而变化,均为K(x);③缓冲器偏压刚度定义为使缓冲器受压面产生单位偏转所需的偏转力矩。设缓冲器沿x轴方向矩形截面的边长分别为2L和b,可以得到缓冲器的受压面刚度密度为

(1)

分别采用解析法和离散法求解缓冲器偏压刚度的分析示意图,如图3所示。图3(a)为采用解析法求解示意图,阴影部分为缓冲器沿y轴的微分dy,其对应的受压面积为dS,假设前从板偏压作用下缓冲器上部受压面产生单位偏转,则dS产生的向上支承力为

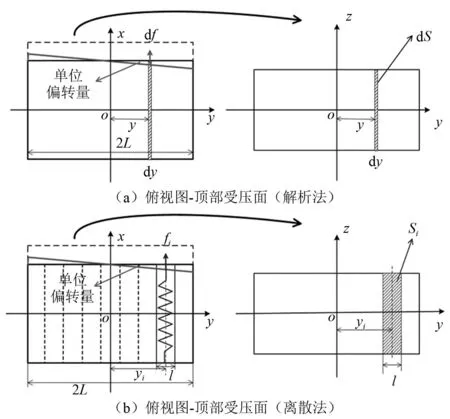
图3 缓冲器偏压刚度分析示意图Fig.3 Schematic diagram of the side-pressure stiffness of draft gear

df=kydS=kbydy

(2)

通过积分可以得到缓冲器受压面产生单位偏转所需的力矩,也即偏压刚度M1

(3)

采用离散法求解示意图如图3(b)所示,假设缓冲器沿y轴方向等间距离散为n(奇数)个具有迟滞特性的阻抗元件,离散力元宽度l和中心线距z轴的距离yi分别为

(4)

(5)

则第i个离散力元对应的受压面积Si为

Si=bl

(6)

同样假设前从板偏压作用下缓冲器上部受压面产生单位偏转,则Si部分产生的向上支承力为

fi=kyiSi=kblyi

(7)

缓冲器受压面产生单位偏转所需的力矩,也即偏压刚度M2为

(8)

通过对比解析法M1与不同离散力元数量的离散法M2便可以确定合适的离散力元数量。NC390型缓冲器截面长度半径为260 mm,离散法中n=3,5,7,9,11,13,15,表1分别列出两种方法计算所得缓冲器偏压刚度。由表1可知,随着离散力元数量的增多,离散法所得缓冲器偏压刚度逐渐逼近于解析结果,当离散力元个数为7时,其误差基本为2%。综合考虑离散力元数量增加带来的计算效率问题,可以确定采用7个阻抗力元对缓冲器进行离散模拟。

表1 解析法和离散法计算所得缓冲器偏压刚度列表Tab.1 Side-pressure stiffness of draft gear calculated by analytical method and discrete method

图3给出了102型圆销钩缓装置的动力学模型,忽略相连挂车钩钩头间的相对水平转动,将连挂车钩简化为一个直杆,车钩相对前从板仅具有一个水平偏转自由度;前从板通过缓冲器连接于车体,相对于车体具有纵向和水平转动自由度;缓冲器离散为等距离排列的7个阻抗力元,钩尾钩肩位置通过止挡力元模拟钩肩的接触支承作用。

缓冲器特性采用具有迟滞特性的非线性模型,将缓冲器加载与卸载特性定义为以其行程为变量的加载函数Fu(x)和卸载函数Fl(x),定义切换速度ve为缓冲器阻抗力在加载函数和卸载函数间切换的临界速率,从而避免缓冲器在加载和卸载之间转换时其阻抗力会发生跳跃。同时引入符号函数sign(Δv·x),可以得到缓冲器数学模型

(9)

缓冲器特性函数由7个离散阻抗力元模拟,每一个离散力元的阻抗特性函数根据其对应受压面积与总受压面积的比例确定

(10)

与此同时,缓冲器各离散部分之间还存在明显的剪切效应。一方面缓冲器橡胶材料分子之间的摩擦碰撞会起到耗散能量和衰减振动的作用;另一方面每个离散部分的运动也会受到相邻离散部分的牵制,这对缓冲器整体的偏压刚度会有一定影响[19-20]。缓冲器剪切参数因与其结构、材质密切相关而不容易确定,本文引入缓冲器附加偏转刚度来综合考虑剪切效应对其整体偏压刚度的影响,本文根据车钩偏转角的试验测试结果,不断调整缓冲器附加偏压刚度,通过反复计算并与试验结果对比最终确定车钩缓冲器附加偏压刚度值。

车钩钩肩与支承块存在的间隙Dj决定了车钩自由偏转角的大小,钩肩接触作用力Fj可以通过如下函数模拟

(11)

2 双机重联牵引万吨列车动力学模型

2.1 列车动力学建模

为了研究重载机车与102型钩缓装置在纵向压钩力作用下的受压稳定性和动力学性能,针对机车位于双机牵引单元万吨重载列车重联位置的运用工况,采用多体动力学分析SIMPACK软件,建立了“主控机车+重联机车+C80货车车辆+虚拟货列”编组的动力学计算模型,四节机车之间采用102型车钩连挂模型,C80货车与机车之间采用17号车钩与102型车钩连挂模型,具体模型如图4所示。

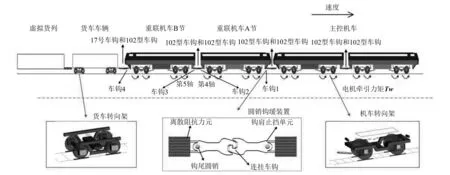
图4 重载列车动力学分析模型Fig.4 Dynamic model of the heavy-haul train

单节机车可简化为由车体、构架、轮对、轴箱、驱动单元等质量体和弹簧、阻尼元件构成的多刚体动力学模型。一系悬挂刚度由轴箱弹簧提供的3个方向刚度和由轴箱定位装置提供的定位刚度组合而成,一系悬挂垂向阻尼则由一系垂向减振器提供;二系悬挂模型主要包括橡胶堆提供的3个方向的二系悬挂刚度、横向止挡刚度、摇头止挡刚度以及垂向、横向减振器提供的阻尼;电机悬挂模型包括电机吊杆及两端橡胶关节提供的6个方向刚度,整个机车动力学模型共计60个运动自由度。货车车辆可简化为由车体、摇枕、侧架、承载鞍、轮对、交叉拉杆等质量体和一系、二系悬挂元件构成的多刚体动力学模型。侧架与承载鞍之间设置一系悬挂力,摇枕与侧架之间设置二系力、止挡力,车体与摇枕之间设置旁承力与心盘力,左右侧架之间还有交叉拉杆力元。

两节机车之间连挂102型钩缓装置子结构动力学模型已经在第3章中建立,而货车与机车之间采用货车车钩与102型车钩连接。C80货车主要装备16/17号可转动车钩,17号车钩通过钩尾球形圆弧面与钩肩限位作用来保证车钩稳定能力,因此本文也建立了102型车钩与17号车钩连挂的动力学模型。17号车钩钩尾同样具有钩肩对中复原装置,可采用式(11)的钩肩与支承块接触力数学模型;另外,钩尾的球面摩擦接触作用通过接触力元来模拟,其数学模型为

(12)

式中:μ为接触面摩擦因数; Δvs为接触点相对运动速度;ves是为了避免摩擦力不连续“跳跃”而设置的切换速度。

机车满级电制时单轴电制动力约为64 kN,根据车轮半径换算成扭矩为40 kN/m,电制动力输入曲线假设为每轴电机扭矩在0～5 s时间内从0线性增大至40 kN/m,在5～30 s时间内始终保持为40 kN/m。不同电制级位的电制动力输入曲线通过该满级电制输入曲线乘以对应级位百分比的方式得到。模型中施加实测得到的重载线路轨道几何不平顺。

2.2 模型中缓冲器附加偏压刚度确定

计算不同缓冲器附加偏压刚度下的车钩偏转角,通过与实测数据对比来确定缓冲器模型中合适的附加偏压刚度数值kq。对比的试验工况为列车以43 km/h通过12号道岔,机车施加40%电制力,102型车钩自由角设置为2.00°,与试验机车相同。

不同附加偏压刚度条件下车钩偏转角的计算结果,如图5(a)所示。当机车制动条件下通过12号道岔时,车钩偏转角将首先达到其初始自由角(2.00°),并在制动力和道岔线形作用下进一步增大,通过道岔区后,车钩偏转角在自由角范围内小幅波动。缓冲器附加偏压刚度对车钩最大偏转角产生一定影响,随着缓冲器偏压刚度的增大,车钩最大偏转角逐渐降低并逐渐趋于其自由偏转角。

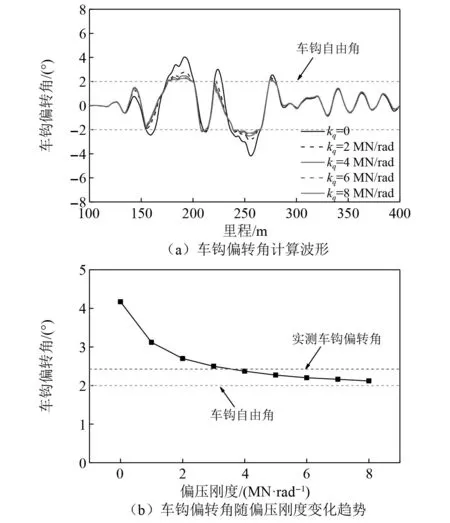
图5 缓冲器偏压刚度对车钩偏转角的影响Fig.5 Influence of buffer deflection stiffness on coupler yaw angle

进一步给出了缓冲器不同附加偏压刚度条件下的车钩偏转角计算结果,如图5(b)所示,当附加偏压刚度在0～3 MN/rad内增加时,车钩偏转角出现明显降低,随着附加偏压刚度的进一步增大,车钩偏转角呈缓慢降低,在此工况下实测的车钩偏转角约为2.35°,对应模型中缓冲器的附加偏压刚度约为3 MN/rad。因此,后续仿真分析中,缓冲器的附加偏压刚度设置为3 MN/rad,并通过脱轨系数等轮轨动力学指标进一步验证该数值的合理性。

2.3 动力学模型验证

为了充分验证模型的正确性、缓冲器偏压刚度参数的合理性,本文分别选取双机重联牵引单元万吨列车通过12号道岔侧线和R600 m曲线的动力学试验数据进行对比分析,试验期间机车所装备102型车钩最大自由转角约为2.00°。根据Zhang等的研究,重载机车侧向过岔动力学性能分析时可将12号道岔侧线简化为具有相同线路线形的S形曲线。模型中12号道岔导曲线曲线半径设为350 m,列车通过速度为43 km/h,机车施加40%电制力。R600 m曲线按照实际设置为两个连续反向R600 m曲线,第一个右曲线参数:超高90 mm,圆曲线长度480 m,缓和曲线长度110 m;第二个左曲线参数:超高90 mm,圆曲线长度230 m,缓和曲线长度100 m,通过速度设为80 km/h。计算所得轮轨力和运行安全性指标均采用“2 m”平滑方式进行处理。

另外,为了说明本文所建立模型在模拟缓冲器偏压特性方面的特点,本文还采用邹瑞明等所述的关联车钩偏转角和缓冲器阻抗力的数学函数的方法建立了不考虑缓冲器偏压特性的动力学模型(称为原模型),并计算了其12号道岔侧向通过工况的动力学响应。

图6和图7分别给出了计算和试验所得重载机车通过12号道岔侧线和R600 m曲线时的车钩转角、脱轨系数、轮轴横向力波形图。由图6和图7可知:两种线路工况下本文模型计算结果与试验数据相比都具有一致的变化趋势,车钩转角最大值都在2.50°以内,脱轨系数最大值未见明显差异,表明该模型能够较好地模拟双机牵引万吨列车重联机车及其钩缓装置在受压环境下的动力学响应。

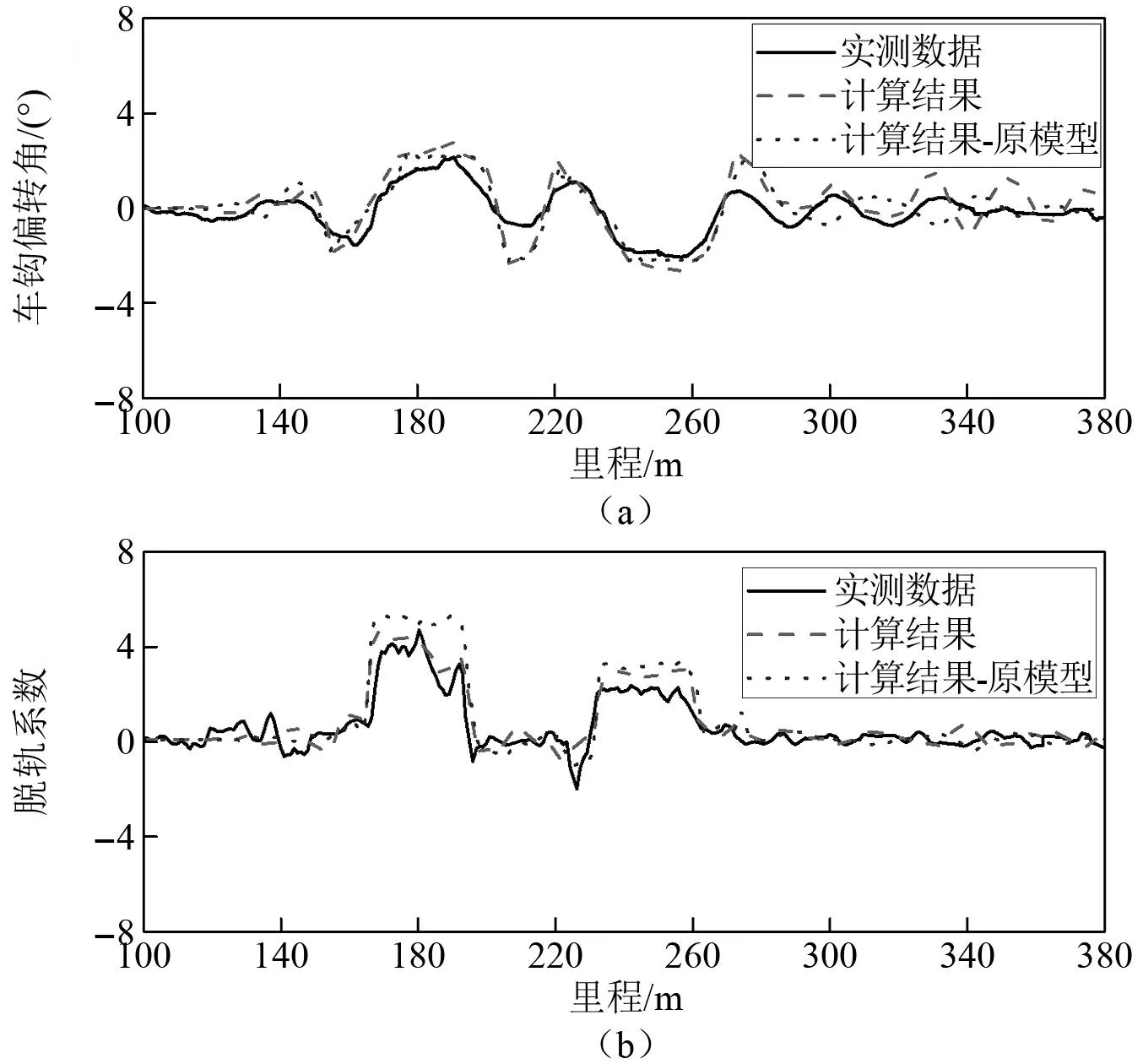
图6 12号道岔侧线通过工况计算和试验波形图Fig.6 Calculated and measured results for the 12 type turnout branch case

图7 R600 m曲线通过计算和试验波形图Fig.7 Calculated and measured results for the R600 m curve case

另外,从图6还可以看出:原有不考虑缓冲器偏压特性的模型所得车钩偏转角在通过道岔导曲线区段基本保持最大自由转角状态,未体现出因缓冲器偏压而产生的额外车钩偏转;而本文模型的车钩偏转角在道岔导曲线区段能够体现出缓冲器偏压产生的额外偏转角,与试验测试结果更吻合,也说明了根据与实测结果对比得到的缓冲器偏压刚度数值是合理的。与本文模型相比,原模型的车钩偏转角偏小,而其机车脱轨系数相应略大。这说明本文所建立102型钩缓装置动力学模型具有更高的准确性和可靠性。

3 动力学性能分析

在验证所建立重载列车动力学模型后,本章采用该模型计算了不同线路条件、结构参数和机车电制力下的系统动力学响应,分析了直线和曲线上系统动力学特性以及结构参数的影响规律,探讨了该重载机车及102型钩缓装置的重载适应性问题。

3.1 直线和曲线上动力学特性

针对直线线路机车90%电制、300 m半径曲线线路机车90%和80%电制三种工况,分别计算重联机车及其钩缓装置的动力学响应,图8和图9分别给出了第2位和第3位车钩偏转角、第4轴和第5轴位轮轴横向力的动态响应波形图。图10给出了不同线路工况下机车与车钩可能出现的几何相对位置关系示意图。可以看出,直线线路上,如图10(a)所示,102型车钩受到较大纵向压钩力作用时会发生水平偏转,机车车体与车钩纵向中心线会呈“之”字形分布,此时第2位和第3位车钩偏转角大小相当,且会对各自相邻车体端产生向外顶推的横向分力,使机车第4轴和第5轴产生大小相当、方向相反的轮轴横向力。

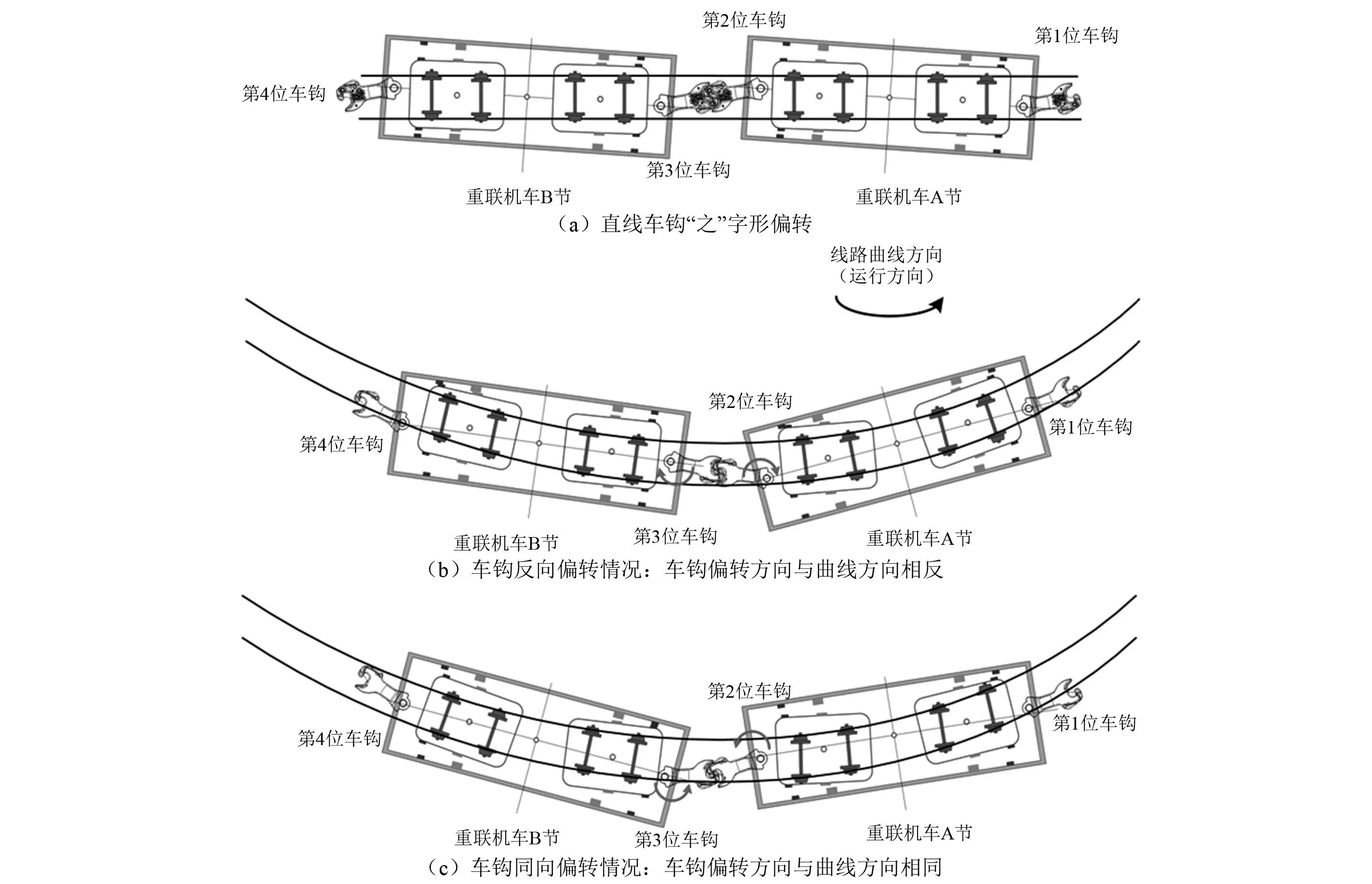
图10 曲线线路上机车与车钩运动关系示意图(左曲线)Fig.10 Kinematic relationship between locomotive and coupler on curves (Left-hand)

曲线线路上,由于线路曲线方向和车钩偏转方向存在不同组合方式,因此系统动力学特性相对较为复杂,这里结合图10的机车及车钩相对运动关系示意图进行说明。曲线上机车电制动力大小及施加时间都会直接影响机车与其车钩相对运动关系和轮轨相互作用力,存在以下两种不同情况:①当机车在进入曲线以后才施加电制动力或者进入曲线前施加较小电制动力时,连挂车钩在进入曲线时所受纵向压钩力较小,此时受机车车体摆动和线路曲率变化的影响,重联机车连挂车钩相对各自车体会出现顺时针方向偏转,第2位车钩会将A节机车后端顶向曲线外轨,而第3位车钩将B节机车前端顶向曲线内轨,表现出随线路变化的跟随性,从而使A节机车后端受到指向外轨的车钩横向分力,而使B节机车前端受到指向内轨的车钩横向分力,即图10(b)中车钩反向偏转情况。这里机车80%电制力工况就属于该情况,此时第2位车钩偏转角达到最大受压自由转角,而第3位车钩偏转角由于曲线线路影响有所减小,A节机车第3、第4轴轮轨横向作用有所增强,而B节机车第5轴起导向作用的轮对轮轨横向作用反而会一定程度减小;②当机车在进入曲线前的直线区段已施加很大电制力且车钩呈现与曲线方向相同偏转方向时,连挂车钩在进入曲线后由于较大纵向压钩力作用无法改变偏转方向,使其始终处于同向偏转状态,丧失了随线路变化的跟随性,即图10(c)中车钩同向偏转情况。这里机车90%电制力工况就属于该情况,此时第2位车钩将A节机车后端顶向曲线内轨,而第3位车钩将B节机车前端顶向曲线外轨,从而使机车所受车钩横向分力呈现完全相反的状态,A节机车后端会受到指向曲线内轨的横向分力,而B节机车前端会受到指向曲线外轨的横向分力,此车钩横向分力和轮轨导向力的综合作用会使第5轴轮对轮轨横向作用显著增强,其轮轴横向力明显增大。

通过本节分析可知,当重联机车在较小纵向压钩力作用下进入小半径曲线时,102型钩缓装置会产生跟随线路曲率变化的反向偏转,使机车非导向的第4轴运行安全性指标增大,而具有导向作用的第5轴运行安全性指标有所减小;而当重联机车在受较大纵向压钩力作用且已发生车钩同向偏转情况下再进入小半径曲线时,车钩极有可能因无法跟随线路曲率变化而保持同向偏转状态,从而使机车第5轴在车钩横向分力和轮轨导向的综合作用下出现异常增大的轮轨横向作用和运行安全性指标,危及行车安全。因此小半径曲线上车钩同向偏转情况更为危险,建议重载列车通过小半径曲线时需严格控制机车车辆的纵向压钩力。

3.2 结构参数影响

本节通过直线、300 m半径曲线两种工况下不同车钩受压最大自由转角、机车二系悬挂横向刚度时系统动力学响应计算与对比,分析系统结构参数的影响规律。直线线路上机车施加100%电制力,300 m半径曲线线路上机车施加80%电制力。

设车钩自由转角在2°～8°内间隔1°变化,分别计算不同车钩受压最大自由转角下的车钩偏转角和机车运行安全性指标。图11和图12分别给出了直线、300 m半径曲线工况下车钩偏转角、机车脱轨系数和轮轴横向力最大值随车钩最大受压自由转角的变化曲线图。可以看出,直线工况下:2位车钩和3位车钩偏转角的数值相当,且随着车钩最大受压自由转角的增大而逐渐增大;机车第4轴的运行安全性指标略大于位于导向位的第3轴、第5轴,且也都随最大受压自由转角逐渐增大。300 m半径曲线工况下:车钩在机车80%电制力时均发生与线路曲线方向相反的偏转,2位车钩保持最大受压自由转角状态偏向外轨方向,而3位车钩偏向内轨方向;此时车钩偏转角均随其最大受压自由转角增大而增大,机车第3轴、第4轴运行安全性指标基本上也都逐渐增大,但由于受到3位车钩指向内轨方向的横向分力作用,机车第5轴运行安全性指标却随最大受压自由转角逐渐减小。总体来看,不管直线还是小半径曲线线路,车钩偏转角、机车运行安全性指标基本上都随着车钩最大受压自由转角增大而增大,应当合理控制车钩最大受压自由转角的大小。

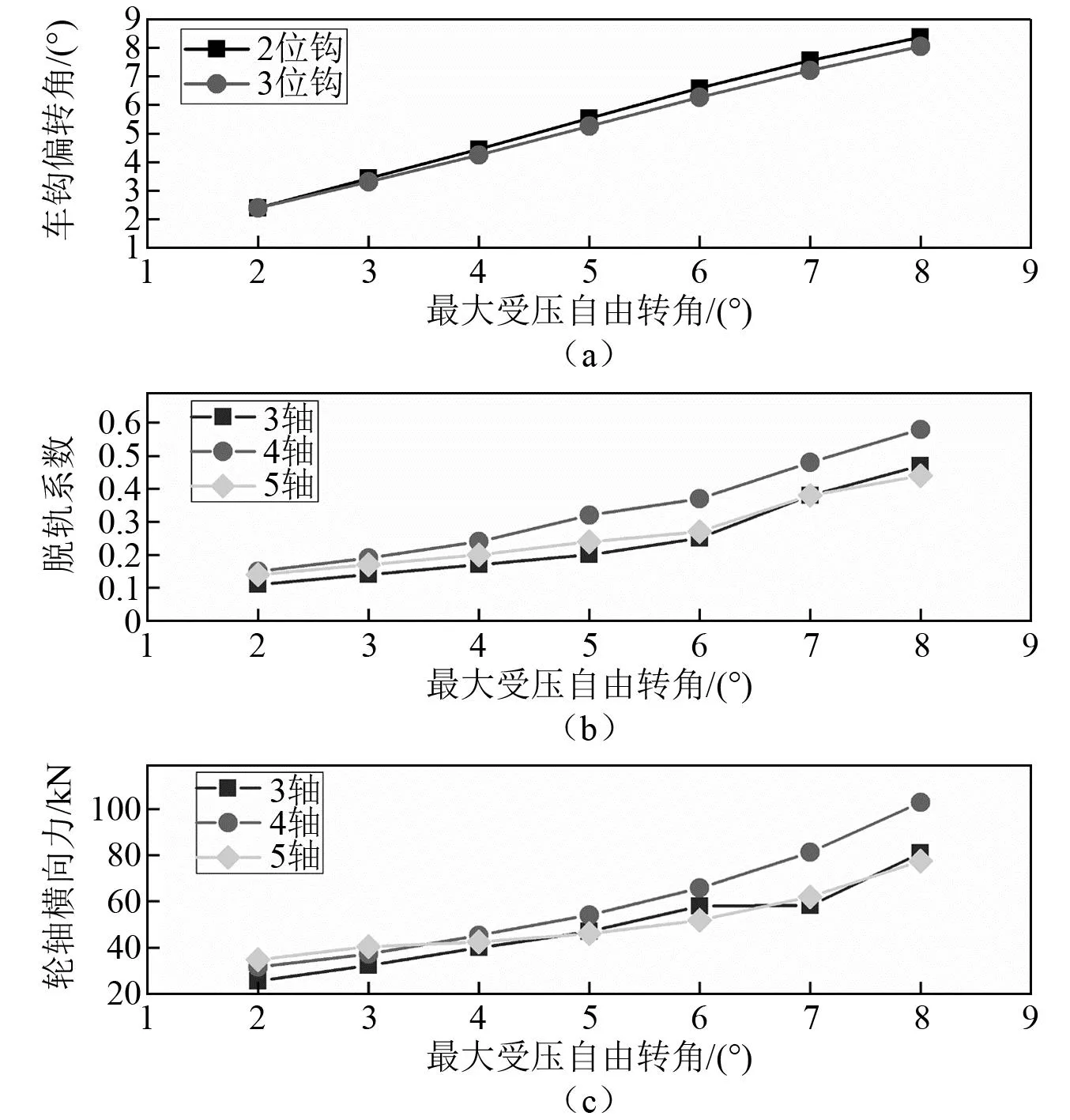
图11 直线上系统响应最大值随车钩最大受压自由转角变化曲线图Fig.11 Influence of coupler’ free angle on the system response on straight line

设机车二系悬挂横向刚度在0.1～1.0 MN/m内变化,分别计算不同二系横向刚度下的车钩偏转角和机车运行安全性指标。图13和图14分别给出了直线、300 m半径曲线工况下车钩偏转角、机车脱轨系数和轮轴横向力最大值随二系悬挂横向刚度的变化曲线图。可以看出,随着机车二系悬挂横向刚度的增大,直线和300 m半径曲线上车钩偏转角都呈逐渐减小趋势,并且当横向刚度增大至一定水平时,机车自身受压稳钩能力得到显著提升,从而使车钩处于相对稳定的对中状态,不再需要车钩钩肩发挥止挡作用。机车运行安全性指标在直线和300 m半径曲线上却会表现出不同的变化规律,直线线路上,轮轴横向力均随二系悬挂横向刚度增大出现先增大后减小的变化趋势;而300 m半径曲线上,受车钩反向偏转的影响,第4轴脱轨系数、轮轴横向力随二系横向刚度增大而逐渐减小,第5轴运行安全性指标逐渐增大。总之,机车二系悬挂横向刚度对102型钩缓装置受压稳定性和机车运行安全性具有较为明显的影响,二系悬挂横向刚度增大有助于提高机车自身的受压稳定性和减小车钩偏转角,但过大横向刚度又会增大轮轨横向动态作用,不利于机车运行安全性。

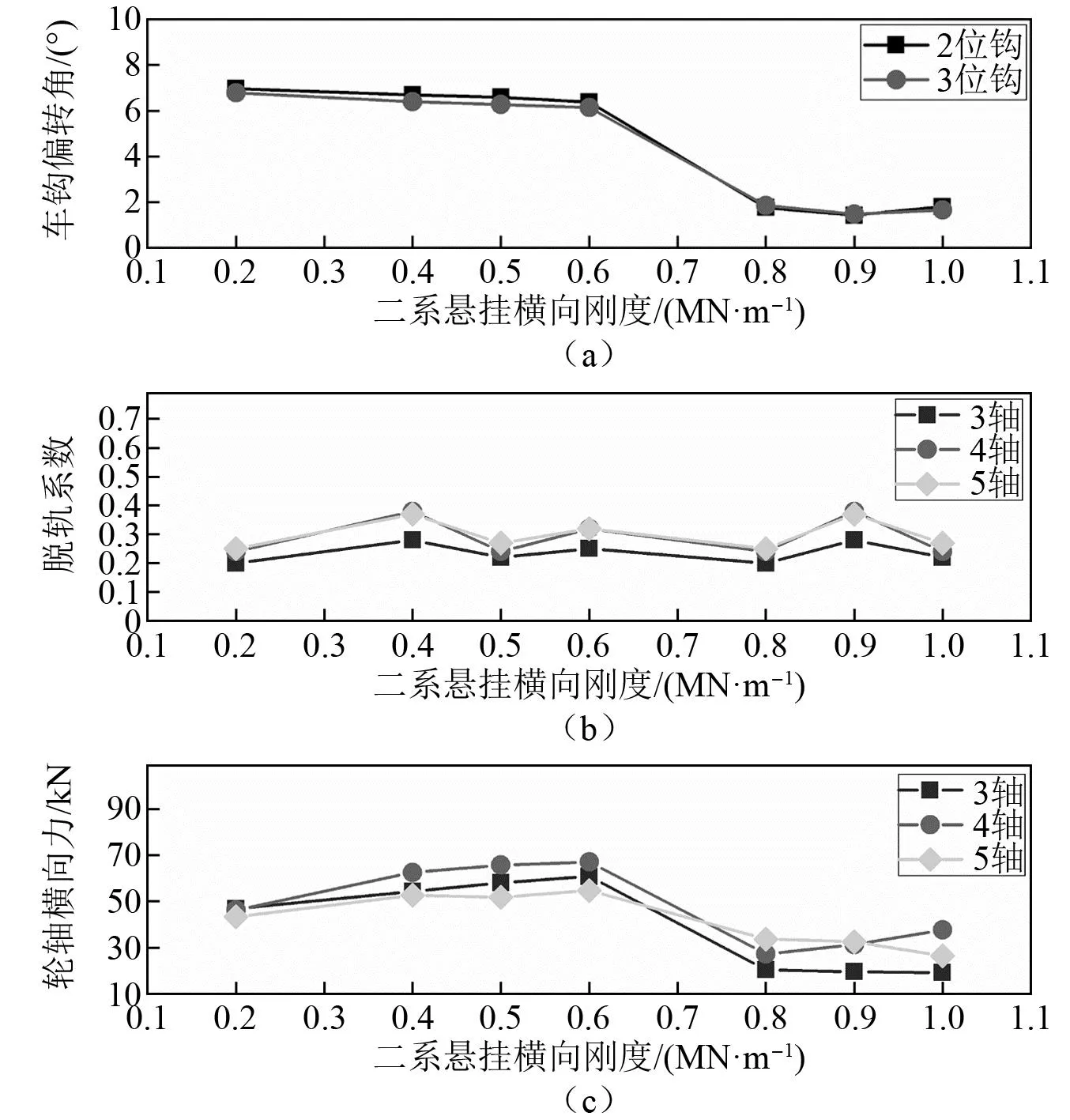
图13 直线上系统响应最大值随二系悬挂横向刚度变化曲线图Fig.13 Influence of secondary lateral stiffness on the system response on straight line

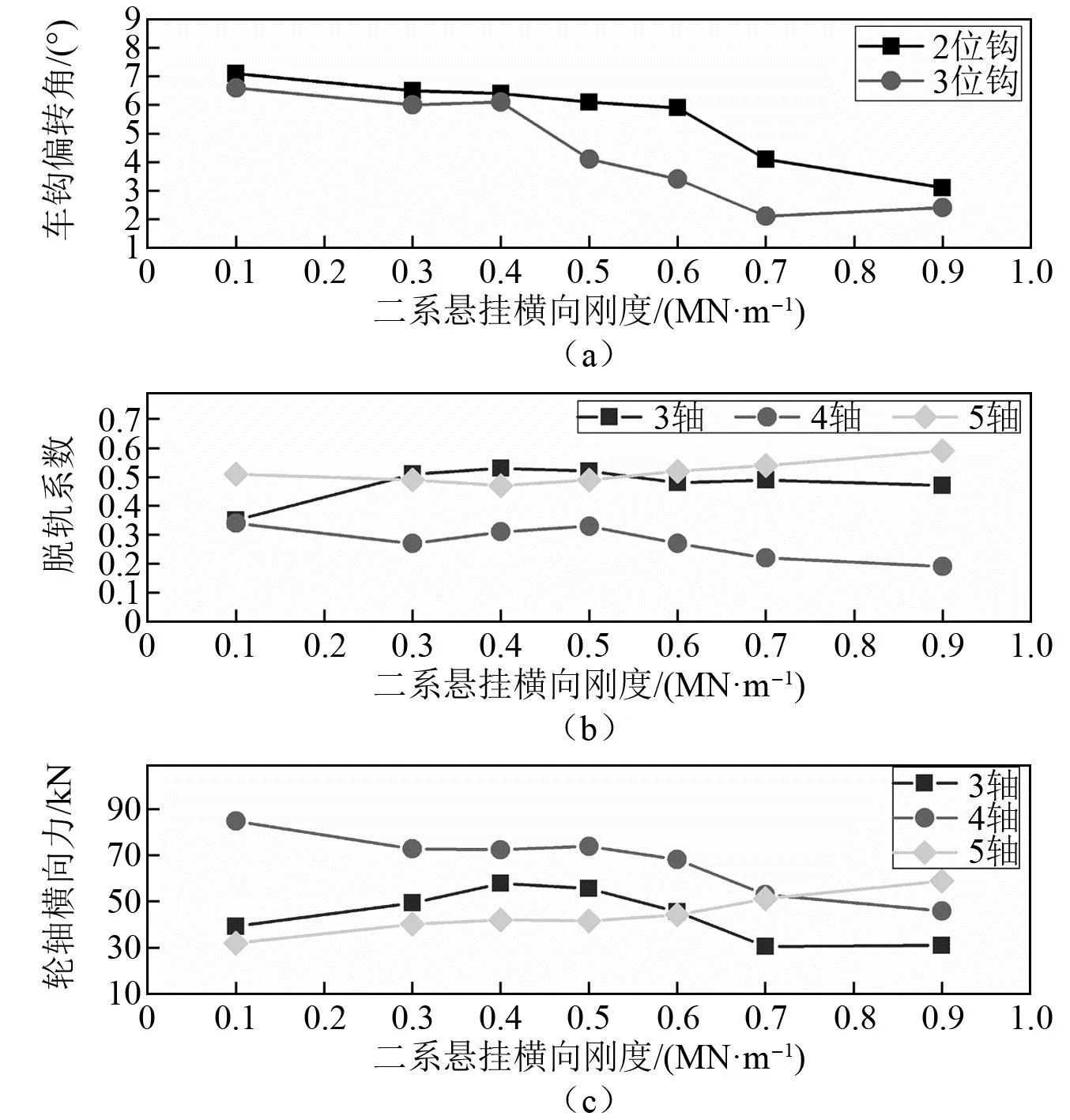
图14 R300 m曲线上系统响应最大值随二系悬挂横向刚度变化曲线图Fig.14 Influence of secondary lateral stiffness on the system response on R300 m radius curve

4 结 论

针对重载机车及其102型钩缓装置的动力学模拟与分析问题,本文采用加权离散等效方法模拟了102型圆销车钩钩肩止挡和缓冲器偏压特性,建立了双机重联牵引万吨列车动力学分析模型,在验证模型正确性基础上,计算了不同线路条件、结构参数的系统动力学响应,分析了直线和曲线上系统动力学特性以及结构参数的影响规律。主要结论包括:

(1) 本文所建立的102型钩缓装置动力学模型能够模拟钩肩止挡和缓冲器偏压特性,具有较高的准确性和可靠性。

(2) 车钩最大自由转角对重载机车运行安全性具有明显影响,随着车钩最大自由转角的增大,车钩偏转角和机车运行安全性指标均呈逐渐增大趋势;机车二系悬挂横向刚度也具有一定影响作用,二系悬挂横向刚度增大有助于提高机车自身的受压稳定性和减小车钩偏转角,但过大横向刚度又会增大轮轨横向动态作用。

(3) 重载机车在较大机车电制力下通过小半径曲线时容易发生车钩偏转方向与曲线方向相同的情况,使机车运行安全性指标显著增大,建议重载列车通过小半径曲线时需严格控制机车车辆的纵向压钩力。