基于振动信号PSD-SVM方法的不定负荷下柴油机气阀间隙异常故障诊断

聂浩淼, 车驰东

(上海交通大学 船舶海洋与建筑工程学院,上海 200240)

柴油机是现代工业、船舶等领域主要使用的动力装置之一。如何能及时发现柴油机故障是排除故障、实现设备高可靠性运转不可缺少的一环。传统的柴油机故障诊断主要有热力参数法、油液分析法与振动测试法。热力参数法加装的缸内压力传感器等部件需要对柴油机进行一定的结构破坏,油液分析法加装的分析系统布置较为复杂,且能识别的故障有限,而振动测试法布置的振动加速度传感器安装简单,采集到的信号蕴含信息丰富,对于机械的结构异常、磨损以及如单缸失火等柴油机缸内异常都有很好的识别手段,因此基于振动信号的柴油机故障诊断是目前一种有效的诊断方案。

使用信号分析方法处理振动信号是一种研究故障诊断的经典方法。该方法使用时频分析[1]、小波分析[2]、模态分解[3]等方法对振动信号进行处理,找到信号时域或频域的特征,通过对柴油机运转机理的了解或者模型推理等方式,判断故障与特征的相关关系或因果关系。对于通过缸盖振动信号诊断气阀故障,早期已有学者证明其可行性[4]。郑毅等[5]基于柴油机配气相位图,使用希尔伯特-黄变换处理柴油机缸盖振动信号,成功提取出信号中包含气阀漏气故障的特征。杨东等[6]针对平稳过程和线性系统,提出了一种提取时域与频域的特征矩阵,利用相关分析与敏感度分析方法诊断柴油机撞缸、失火和小头瓦磨损故障。贾翔宇等[7]采集缸盖振动信号,利用压缩小波变换实现对柴油机失火故障特征的提取以及故障的识别定位。经典的信号分析方法的优势在于对于样本数量与分布的要求不高,对于许多难识别的故障也有针对性的诊断方法,而其缺陷在于对于故障特征提取的效率低,依赖于研究者的主观判断,并且许多方法并未深入对不同工况下的同一故障进行诊断。随着计算机技术的发展,机器学习逐渐成为一种重要的诊断方法。

使用机器学习的诊断方法往往需要大量的带有标签的样本用于训练机器学习模型。模型会通过结果与样本标签的差异来修正模型参数,使其在训练集中误差极小。廖舒琅等[8]提出一种基于图卷积神经网络(graph convolutional network, GCN)的方法诊断柴油机喷油异常与断缸故障。刘东川等[9]使用一种改进的深度森林模型来诊断旋转机械中滚动轴承的故障。张俊红等[10]使用一种改进的卷积神经网络(convolutional neural network, CNN),对包括进排气阀间隙异常在内的诸多故障进行诊断研究,取得良好诊断结果。这些研究在柴油机单一转速与负荷的条件下实现了对故障的准确识别,但在其他工况下并未进行深入研究。当柴油机负荷改变时,其整体振动情况也会随之改变,进而导致一部分特征出现变化,使得某些故障无法用原本方法进行诊断,因此研究变负荷下的故障诊断方法具有一定意义。

为了实现在不同负荷下的故障诊断,本文提出了一种将原始振动信号的功率曲线通过滑动平均滤波(moving average filter, MAF)与标准化,去除由于柴油机负荷改变造成的振动整体性能量变化,通过计算功率谱密度(power spectral density, PSD)提取标准化信号每个发火周期的特征,将数量少、维度大的样本转化为数量多、维度小的样本,使用这些样本训练支持向量机(support vector machine, SVM)模型,来实现在不同柴油机负荷下进排气阀间隙异常的诊断。

1 PSD滤波标准化信号特征提取与分类方法

1.1 短时傅里叶变换

傅里叶变换能将时域信号转化为频域信息。通过振动传感器采集到的离散时域信号可以通过离散傅里叶变换(discrete Fourier transform, DFT)处理。为了能够观察频谱随时间的变化,可采用短时傅里叶变换(short-time Fourier transform, STFT),用窗函数限定DFT范围,通过计算窗口滑动时的频谱来进行分析,可以用检波时间Ts表示窗口的时间长度[11]。离散STFT表示为

(1)

1.2 滤波与信号标准化方法

柴油机振动信号为功率信号,能计算信号的功率变化。离散信号的功率计算公式为

(2)

式中:x为时域向量;T为对应的时间长度。

对于原始振动信号的功率变化,使用滑动平均滤波能过滤由于燃烧、转速、外界干扰等因素对信号的影响,并且在滤波前后总能量不变,因此使用MAF滤波对信号功率进行有限脉冲响应的滤波,其计算公式为

(3)

1.3 通过相似度评价特征

好的特征应该满足属于同一状态的特征之间相似度高,属于不同状态的特征之间相似度低。余弦相似度能表示两向量在欧式空间内方向的同向程度,向量a与b的余弦相似度为

(4)

向量范数能表示两向量之间误差的大小,常用的L2范数计算公式如下

(5)

1.4 SVM分类

SVM是一种经典的机器学习算法,该算法通过寻找一个决策超平面来对两个欧式空间内的向量集合进行划分[12]。对于标签不同的两个向量集合X1与X2,决策面f(x)=wTx+b应当满足

wTx1+b>0,wTx2+b<0,x1∈X1,x2∈X2

(6)

有时两集合可能存在少数样本越过决策面,但对于大部分样本线性可分,此时可以对样本进行松弛处理,在优化目标上加上损失函数,使优化目标改变为

(7)

式中:C为惩罚系数;ξ为引入的松弛变量,约束改变为yi(wxi+b)≥1-ξi。

对于一些样本集合在原本的维度不具有线性可分性,核方法SVM能对样本进行升维,在高维空间中使用超平面进行划分,其公式如下

wTφ(x)+b=0

(8)

式中,φ满足

K(x1,x2)=φ(x1)·φ(x2)

(9)

K被称为核函数,使优化过程中计算高维向量的内积能通过低维向量的运算完成。本文中使用高斯核函数,其公式如下

(10)

式中,σ为高斯核的带宽,为方便计算,可取2σ2=1 。

2 柴油机气阀间隙故障试验模拟

2.1 试验台架与测试系统布置

为验证不同负荷条件下算法对柴油机气阀间隙故障的诊断有效性,本试验选择一台六缸四冲程柴油机,额定转速为1 500 r/min,气缸编号为A1～A3,B1～B3,在每个缸盖上布置振动加速度传感器,故障模拟台架与振动测试系统具体布置如图1与图2所示,图中A1～A3测点在柴油机背面,与B1～B3测点对称。

图1 故障模拟试验台架Fig.1 Fault simulation test bench

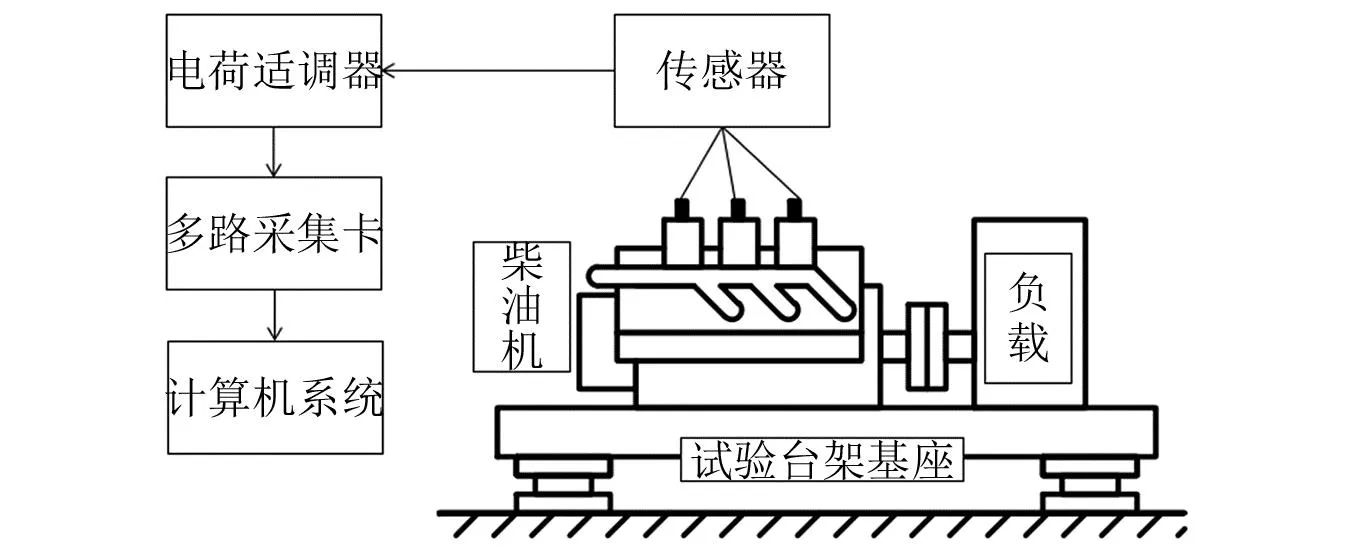
图2 振动测试系统布置示意图Fig.2 Schematic diagram of test bench and test system

测试系统通过六个布置在缸盖的传感器采集振动加速度信号,传感器的电荷通过电荷适调器转换为采集卡记录的电压信号,再通过多路采集卡汇总至计算机供研究分析,测试系统部件型号如表1所示。

表1 测试系统部件Tab.1 Test system components

2.2 测试方案与数据获取

试验选择 25 600 Hz 采样率,故障模拟在B1缸内,在柴油机平稳运行的情况下进行随机多次长度为1 s的连续采样。为保障算法在柴油机各个负荷下诊断的普遍性,以25%负荷为间隔,测试不同负荷下柴油机缸盖振动信号,每个工况测试次数不少于3次,具体的测试方案如表2所示。

表2 测试方案Tab.2 Experimental program

根据测试方案获得柴油机振动信号样本集,其中一段柴油机满负荷正常运行时B1缸振动样本如图3所示,可见从时域信号来看难以直接区分故障。以一个发火周期为时间窗口宽度计算故障状态下的功率谱响应如图4所示,可见气阀间隙异常时在1 200 Hz附近的能量会增加,能够一定程度上直观看出响应上的异常。

图3 原始振动信号对比Fig.3 Raw vibration signal

图4 振动响应PSD对比Fig.4 Vibration response PSD comparison

3 特征提取与故障诊断

3.1 滤波参数的选取

数据处理过程的主要参数为短时傅里叶变换的检波时间Ts、覆盖率η、采样率Fs、转速r和功率谱计算与滤波的时间窗口长度T,这些参数的确定方式如表3所示。

表3 滤波参数表Tab.3 Filter parameters

这些参数中覆盖率影响时频分析中频谱在时间轴上的粒度,越接近100%的覆盖率会使计算量越大,此处取覆盖率为90% 足够进行分析。其余自定参数中,检波时间Ts与滤波窗口T的选取均与转速有关,这些参数的选择方法如下:

(1)转速r。一般情况下,转速由其他渠道提供,如在试验台架上,转速为自己设定,在实际船舶上,转速由设置在轴系上的传感器确定。但在特殊场景,如需要通过柴油机发火能量计算转速的场景中,也可以通过功率谱分析进行确定。假设本六缸四冲程柴油机的转速在1 000～3 000 r/min,对应六缸依次发火的完整周期范围为0.04～0.12 s,取0.06 s为检波时间,计算在两倍检波时间的MAF滤波窗口下的波形如图5所示,再分析滤波后信号的频率,可以发现激励频率约为12.5 Hz,对应的六缸依次发火频率为75 Hz,周期约为0.08 s,与实际情况相符。

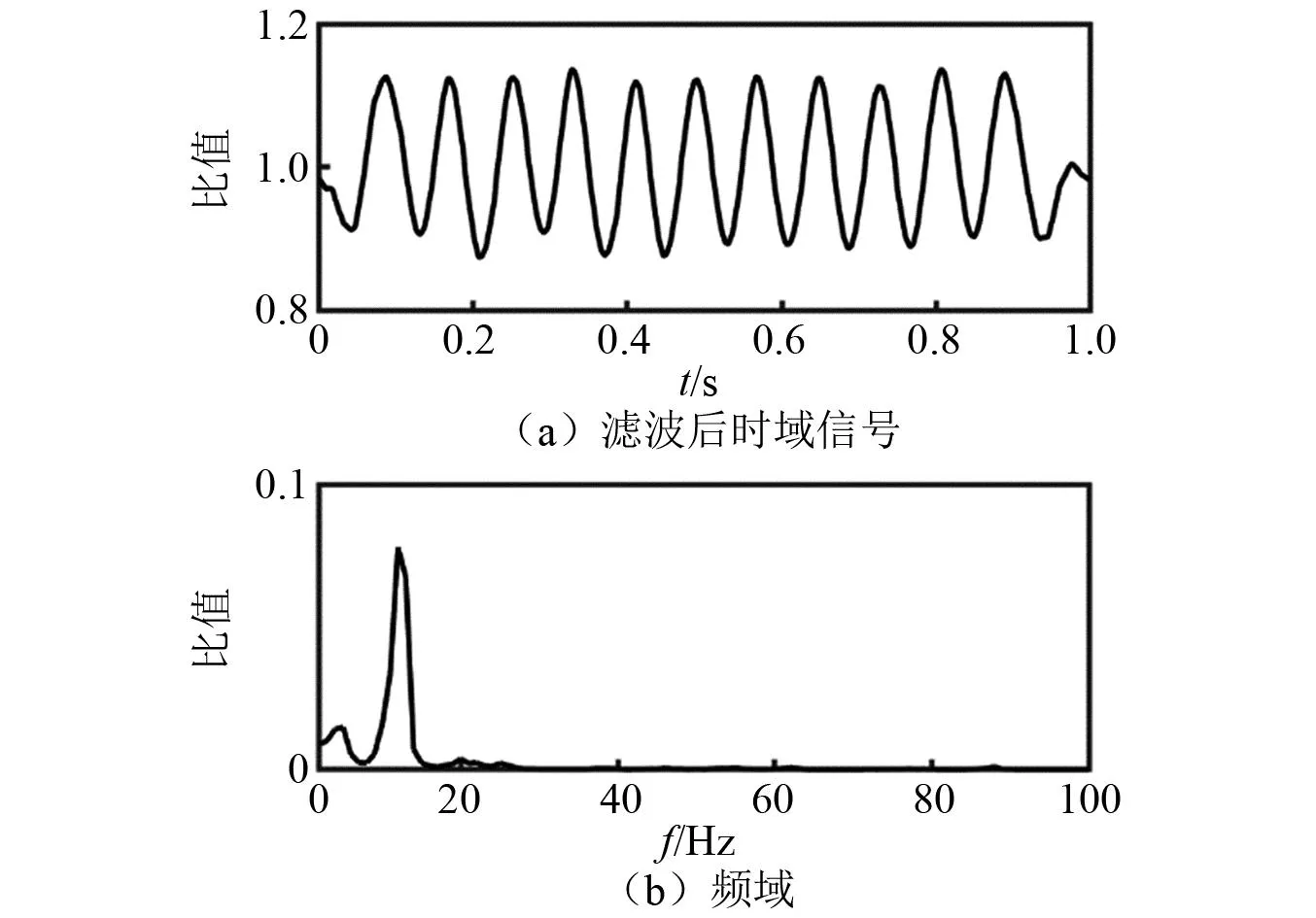
图5 转速的识别Fig.5 Identification of rotation speed

(2)检波时间Ts。检波时间的选择通常与转速和需要诊断的故障有关。对于六缸柴油机缸内发生的故障,设置检波时间为五缸发火所用时间,通过缺少的一个单缸发火周期来尝试捕捉故障缸的异常信号。已知柴油机转速为1 500 r/min,六缸依次发火周期为0.08 s,故设定检波时间为0.066 67 s。不同检波时间对功率谱的影响如图6所示,可见以柴油机六个气缸完全发火周期的单缸发火周期倍数偏移为检波时间时,功率谱能保证明显的周期性,而以完全发火周期为检波时间时,不易分析其周期性。

图6 不同Ts对信号功率周期性的影响Fig.6 The effect of different detection time

由于采样时间固定为1 s,检波时间越长,能分析数据块数量越少,而若检波时间过短,信号中正常部分占比变大,会导致故障工况与正常工况的功率谱的差异减小。综合考虑,检波时间可设定为三缸～五缸的发火周期。本文选择检波周期等于五缸的发火周期0.066 67 s。

(3)滤波窗口T。通常滤波窗口的宽度在六个气缸完全发火周期的附近。滤波窗口越小,滤波结果与原信号差别越小,最终结果更偏向反映更细致的特征,滤波窗口越大时,功率的低频变化影响更大,最终结果包含的宏观特征更多。观察表4,滤波后正常、排气阀故障、进气阀故障三种工况信号之间的差异较为显著。如果通过数据进行故障识别,在时间窗口较小时,所得信号的无关信息更少,更易于进行数据分析,故选择时间窗口为0.013 33 s。

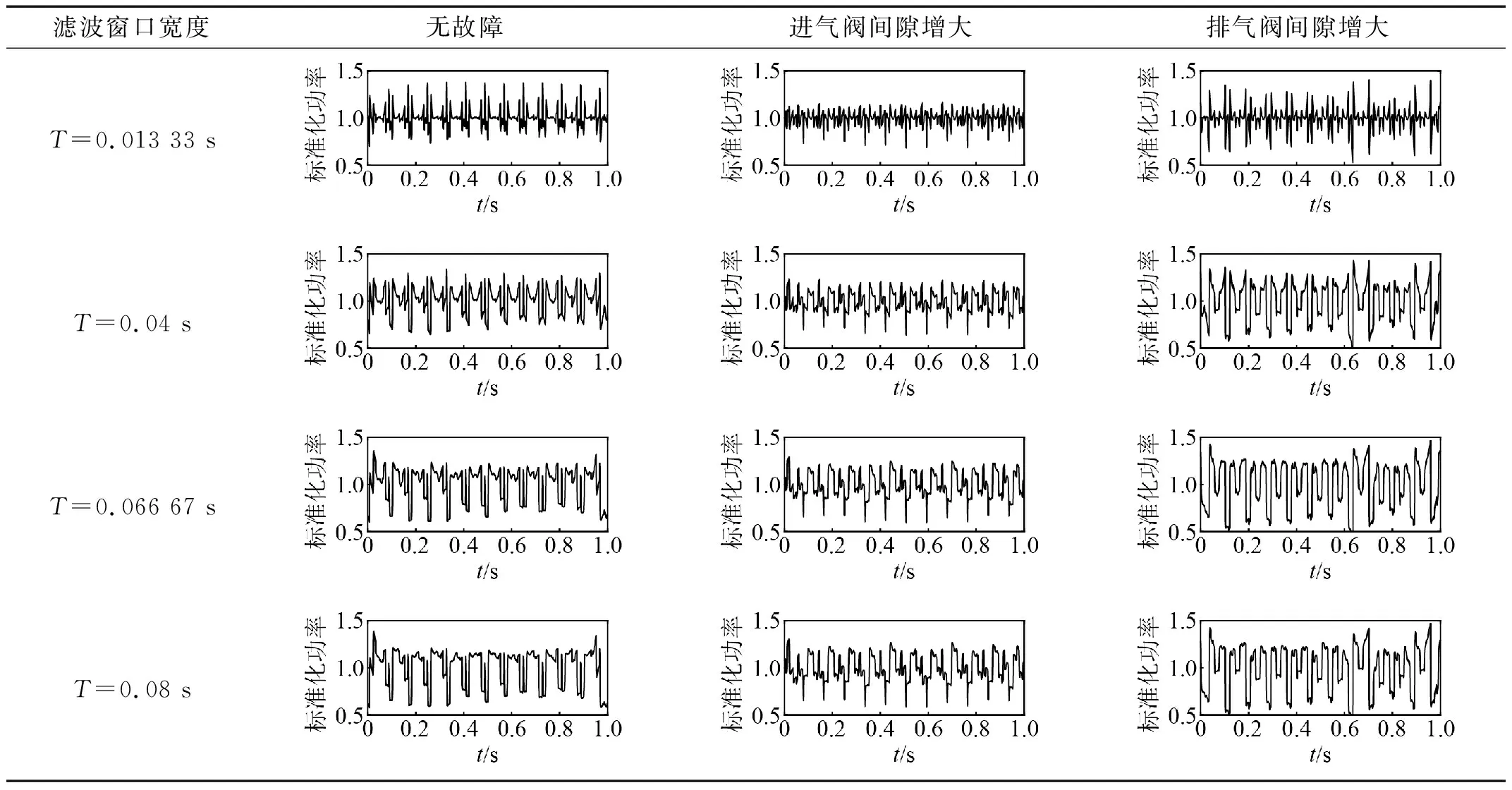
表4 各状态滤波结果对比Tab.4 Filter results for each state

3.2 样本特征的提取与标准化处理

由于取滤波时间窗口为0.013 33 s时,滤波结果在常数1附近震荡,并且结果为无量纲值,因此可将其平移至0附近,最终得到信号的标准化周期性样本,以柴油机满负荷工况为例,取其中一个周期计算PSD作为特征,三个状态的特征如图7所示,由于PSD能量主要集中于200 Hz以下,因此此处只展示1 024 Hz以下的PSD特征。

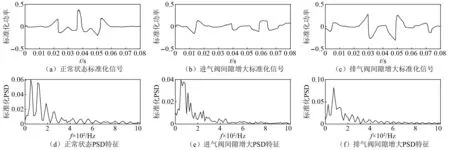
图7 各状态特征Fig.7 The features

每个特征与其对应样本进行相似度比对,跳过采样窗口开始与末尾处被循环处理的数据,可以得到其自相似度曲线,将特征与其他工况标准化PSD交叉比对,可以得到相似度交叉比对结果。考虑到负数情况,统计相似度平方作为特征与样本之间的相似度,得到表5。可以发现正常状态与故障状态之间的相似度区分较大,而通过故障特征与故障样本之间匹配的相似度差异并不明显。由此可知,使用正常特征去判别信号,能明显识别出信号是否正常,在此基础上,若识别为故障信号,仅使用相似度计算难以通过故障特征的匹配程度来区分进排气阀间隙增大两种故障。

表5 特征与样本相似度Tab.5 The of features and samples

3.3 基于SVM的分类

通过信号处理的方法,能得到不同负荷、不同状态、不同缸的振动信号特征,但是特征不仅与是否产生故障有关,同时也与负荷、气缸位置有一定关系,难以简单地区分,因此采用SVM方法进行故障识别分类。SVM模型只适用于二分类任务,这里通过多个一对多分类器来进行正常、进气阀故障、排气阀故障的特征多分类。

在训练集与测试集相同时进行十折交叉验证,以此测试模型的泛化分类准确率,不同训练集-测试集下,线性SVM对故障诊断的准确率如表6所示,其中横向为在不同测试集下测试,可见在小样本训练、小范围验证时,线性SVM分类具有不错的效果,然而多工况不同测点的分类的准确率较低,这说明柴油机特征序列单缸固定负荷工况样本是线性可分的,多测点复杂工况的样本在向量空间无法线性区分。

表6 线性SVM分类准确率Tab.6 Linear SVM classification accuracy

为了解决复杂工况下特征线性不可分的问题,使用核方法SVM,将特征转化为高维向量后再进行区分,其三分类的区分准确率如表7所示,可见对于布置在故障缸上测点的传感器,核方法SVM在全负荷情况下表现出了良好的识别率,而对于从不同测点的传感器进行识别,模型的泛化表现不尽人意。因此可以使用核方法SVM通过布置在每一气缸上的传感器对于所在气缸进行故障诊断,在可变负荷的条件下其对所在气缸故障的识别率可达0.967 2。

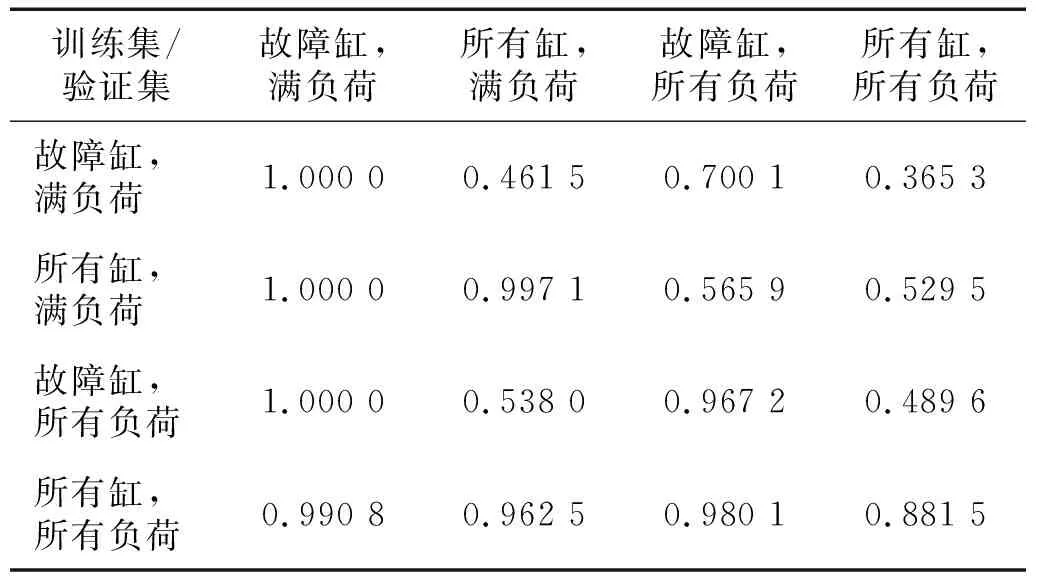
表7 核方法SVM分类准确率Tab.7 Kernel method SVM classification accuracy

由表7数据可知,核方法SVM在检测传感器所在气缸是否故障的单次诊断准确率为0.967 2,而在实际工程中,能通过STFT对传感器连续读取的振动信号不断进行处理,因此实际的诊断效果将更稳定。如果仅考虑正常-故障的二分类诊断,其混淆矩阵如表8所示,可见此时的故障诊断准确率可达0.999 8。对于通过其他缸盖传感器诊断某一气缸内的气阀间隙异常时,在可变负荷下的诊断准确率为0.881 5,其诊断的混淆矩阵如表9所示。由表9数据可知,通过任意缸盖传感器诊断的错误诊断主要来源于两种故障的区分,当仅考虑正常-故障的二分类诊断时,诊断准确率可以达到0.955 4,因此也具有一定使用意义。总的来说,即使负荷情况未知,该方法对于传感器所布置的气缸是否故障的判断准确度高,对于相似故障的区分较高,同时由于机器学习的特性,能够在运行中随着样本数量的增加不断优化识别泛化性与准确度,具有一定的应用价值。

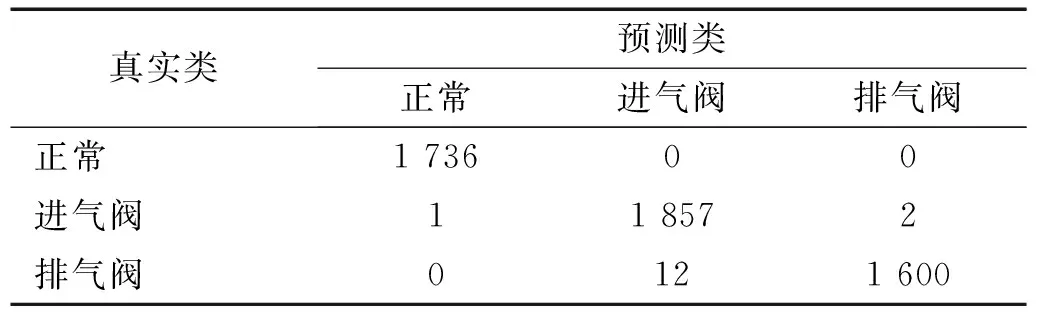
表8 故障缸、所有负荷条件下诊断混淆矩阵Tab.8 Confusion matrix for faulty cylinders, all load

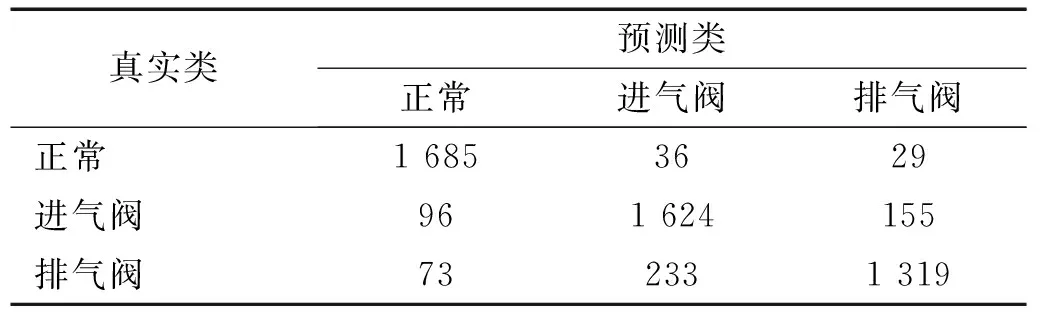
表9 所有气缸、所有负荷条件下诊断混淆矩阵Tab.9 Confusion matrix for all cylinders, all load

4 结 论

本文通过柴油机缸盖振动信号测量数据的分析对气缸内进排气阀间隙故障进行诊断,针对不同负荷下缸盖振动信号,提出了通过MAF滤波处理振动功率信号并将其标准化,再计算标准化功率曲线的PSD并使用核方法SVM识别的故障诊断方法。主要结论有:

(1)通过柴油机满负荷工况训练集得到的SVM模型对其他工况下的测试集诊断准确度很低,证明柴油机负荷的改变能影响故障的特征,在单一负荷下适用的诊断方法不一定在其他负荷下能够准确诊断。

(2)通过所有负荷训练集训练得到的核方法SVM模型对于任意负荷下的气阀间隙故障识别准确率达到0.967 2,证明本文提出的方法能有效识别柴油机不同负荷下的进排气阀间隙异常。

(3)由于特征提取依靠标准化处理与计算PSD,因此在实际信号采集出现延时或者偏移的情况时,本方法依然能正确的提取出供对比的特征,证明本文提出的方法具有一定鲁棒性。