基于信号响应分析模型的金属结构损伤导波检出概率

王 莉, 杨 宇, 刘国强, 王霞光, 李嘉欣, 任一鹏

(1. 南京航空航天大学 航空学院机械结构力学及控制国家重点实验室,南京 210016;2. 中国飞机强度研究所 强度与结构完整性全国重点实验室,西安 710065)

为保证飞机结构安全,飞机结构设计理念经历了由静强度设计、安全寿命设计到损伤容限设计的演变历程[1-2]。在现代军/民机结构强度设计过程中,损伤容限设计思想已经得到了全面应用[3-4]。损伤容限设计思想允许飞机结构在使用过程中出现裂纹,但这些裂纹可以通过采用合适的无损检测手段,确定恰当的检查周期,发现并进行控制,确保在裂纹扩展到不稳定状态之前就能可靠地检测出,从而保证结构发生灾难性破坏的概率降到最小[5]。因此对无损检测技术的损伤检测能力进行定量评价是保证结构安全性的重要手段之一。由美国空军颁布的MIL-HDBK-1823《检测系统的可靠性评价大纲》[6]可知,在一定的检测条件下,结构损伤检测具有一定的随机性,基于统计理论可得到结构损伤检出概率(probability of detection, POD),并可将其作为衡量无损检测可靠性的定量表征指标。

随着柔性电路、信号处理和材料科学等技术的发展,传统的无损检测技术正逐渐被一种先进、新颖的结构健康监测技术(structural health monitoring, SHM)所取代[7-10]。但在结构健康监测技术真正投入军/民用领域之前,该技术的结构损伤监测可靠性还有待进一步考核。目前结构损伤健康技术的可靠性评价方法尚未建立标准,遵循无损检测可靠性的评价思想,结构损伤检出概率POD曲线、受训者工作特征曲线(receiver operating characteristic curve,ROC)和误报率(probability of false alarm,PFA)曲线等均可作为结构损伤监测技术可靠性和鲁棒性的常用表征指标[11]。

结构损伤监测技术旨在利用永久性安装在结构表面的传感器网络,通过连续多次获取监测数据以评估结构健康状态,因此SHM技术的POD与传统无损检测技术的POD不同,主要体现在两种技术POD的影响因素来源不同。对于无损检测技术,影响检测可靠性的主要因素为检测设备和操作人员等外部因素,而影响SHM技术监测可靠性的主要因素为结构几何构型、边界形式、监测方案、传感器老化、环境条件、损伤形态和信号处理方法等内部因素[12]。因此需要针对结构损伤监测技术,开展结构损伤检出概率的理论和试验研究,分析内部因素对结构损伤检出概率的定量影响,辨别主要和次要影响因素,进而指导结构损伤监测方案的制定,提高其工程可靠性,有力保障飞机结构的安全可靠水平[13]。

目前根据检测记录结果,可将结构损伤监测技术的POD分为:检到/漏检(hit/miss)[14]与信号响应(signal response)两种形式。其中:signal response分析模型中结构响应是连续的,其能表达更多的结构状态信息,因此结构损伤监测技术的POD目前主要采用signal response模型进行分析[15]。国内外研究学者关于结构损伤监测技术的POD现已开展了部分理论和试验研究。刘晓同[16]提取导波损伤监测信号的波包能量作为系统响应,采用信号响应分析模型,构建了基于导波损伤监测技术的金属接头结构裂纹损伤和复合材料加筋壁板结构分层损伤的POD曲线。Christine等[17]针对翼梁结构疲劳损伤的导波监测信号,通过提取互相关系数作为系统响应,构建了基于信号响应分析模型的翼梁结构损伤导波监测的POD曲线。进一步通过试验发现,由于试验件间结构材料、疲劳试验加载和传感器粘贴工艺等分散性,导致不同试验件的POD曲线不同,因此提出了考虑试验件间差异的线性混合效应模型的POD计算方法。Monaco等[18]通过假设监测环境中的噪声符合正态分布,定义了损伤敏感因子作为系统响应,并通过噪声环境下多次重复采集的因子得到损伤监测阈值,最终明确了复合材料机翼层合板结构冲击损伤的导波监测能力。David等通过研究发现,特定结构损伤尺寸下,重复监测次数对POD曲线具有一定的影响,且重复监测次数越多,在特定检出概率所对应的可检损伤尺寸则越小。Li等[19]提出了基于模型辅助的POD计算方法(Model assisted POD, MAPOD),首先通过采用物理模型对导波在结构中的传播、散射和环境影响等进行了数字化表达,进而建立了基于蒙特卡洛检验的有限试验样本下信息外推的POD曲线计算方法。Chang等[20]通过试验发现,针对特定结构形式存在一组特定的导波损伤监测POD曲线,且由于试验件间的差异使得不同试验件的POD曲线不同,同时发现基于响应信号所提取的系统响应类型同样依赖于结构形式。

上述研究建立了导波损伤监测技术的POD计算方法,但并未定量分析各种模型参数对POD曲线的定量影响规律,且尚未给出不确定模型参数影响下不同置信度下的典型结构损伤导波监测的POD曲线。因此,本文针对导波损伤监测技术,建立了一种基于信号响应分析模型的结构损伤导波监测可靠性评估方法,分析了损伤指数类型、对应关系拟合函数和传感器网络布设等内部因素对金属开孔和搭接结构疲劳裂纹损伤导波检出概率的定量影响规律,明确了不同置信水平下金属典型结构损伤的导波检出能力。

1 基于信号响应分析模型的导波检出概率计算方法

1.1 基于损伤尺寸与损伤指数拟合关系的导波检出概率计算模型

POD是基于统计学的方法对结构损伤监测结果进行分析,通常POD曲线的测定过程[21]为:①确定POD的计算模型;②基于统计学的方法对监测结果进行记录;③根据记录结果,估计POD计算模型中的未知参数及其置信区间;④根据POD曲线的拟合函数形式,绘制不同置信度下的POD曲线。基于信号响应分析模型的导波监测POD计算模型中记录结果为结构损伤导波监测信号,通过提取导波监测信号的损伤指数,可用于反映监测信号中包含的结构损伤信息。进而通过建立损伤尺寸与损伤指数之间的对应关系得到POD曲线,损伤尺寸与损伤指数之间一般呈对数线性相关[22-23],其可表示为

f(r)=β0+β1f(a)+ε

(1)

式中:f(a)为损伤尺寸a的对数;f(r)为导波监测信号提取的损伤指数r的对数;ε为满足均值为0、标准差为σε的正态分布;β0,β1为线性回归或对数线性回归的拟合参数。

由于监测环境和导波监测技术灵敏度的限制,即使结构中无损伤,也会得到不为零的结构损伤监测信号,直至导波响应信号超出无损伤情况下的损伤指数阈值时,才能判断为该结构存在损伤;而当响应信号小于该监测阈值时,则表示该结构无损伤。因此基于损伤尺寸与损伤指数对应关系的POD(a)计算原理如图1所示,其可以表示为

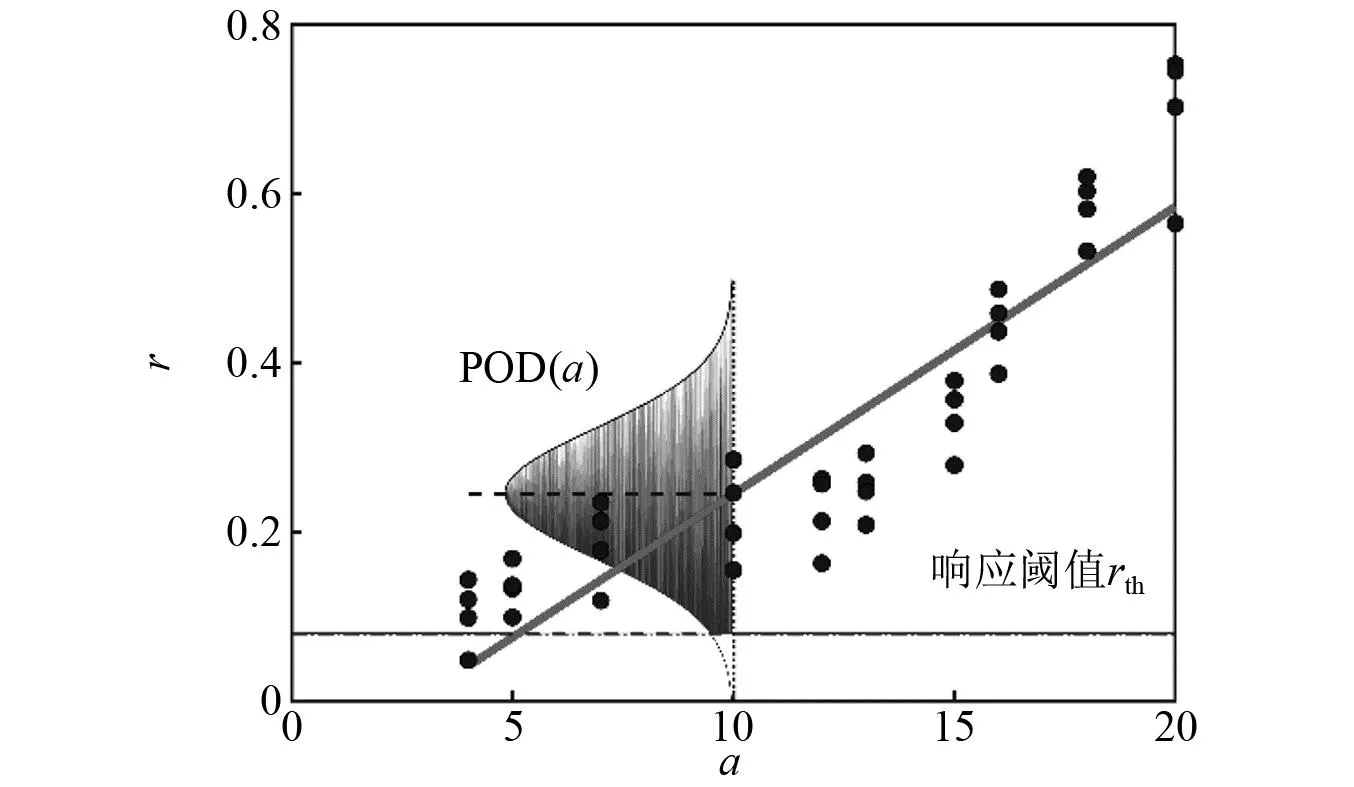
图1 基于信号响应分析模型的POD计算原理Fig.1 Principal of POD computation method based on signal response analysis model

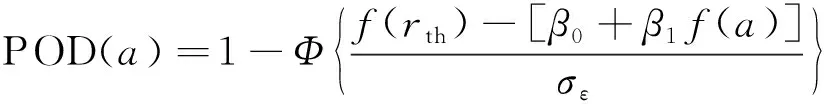
(2)

式中:rth为损伤指数阈值; Ф(·)为标准正态分布函数。

进一步根据正态分布的对称性和监测阈值rth,导波监测技术的POD计算模型可进一步表示为

(3)

式中,μ为标准正态分布函数的均值,可表示为

(4)

式(3)中,σ为标准正态分布函数的标准差,可表示为

(5)

根据式(3)可知,损伤指数阈值rth、拟合参数β0,β1,σε是影响POD计算模型的关键参数。其中,损伤指数阈值rth可在结构无损伤情况下多次采集导波监测信号确定,其可将由于传感器性能退化、环境温度、电磁干扰等因素引起的监测信号干扰波动考虑在内。拟合参数可通过采用最小二乘法拟合损伤尺寸与损伤指数的对应关系得到。

1.2 不同置信度下的导波检出概率计算模型

通过最小二乘法可以得到损伤尺寸a与损伤指数r间的线性或对数线性拟合关系,同时可以得到拟合参数的协方差矩阵Σreg,可以表示为

(6)

由于拟合参数的置信区间直接影响着POD计算模型的置信度,因此利用delta方法可以得到POD计算模型的协方差矩阵Σpod,可以表示为

Σpod=φTΣregφ

(7)

式中,φ为不同置信度下POD计算模型的转移矩阵,可以表示为

(8)

最终根据POD计算模型中未知拟合参数的置信区间,可以定量化评估不同检出率所对应裂纹长度的置信概率。95%置信度下90%检出率所对应的损伤尺寸a90|95,可以表示为

(9)

式中:z0.95为标准正态分布下95%单边置信概率值;u为由标准正态分布下90%单边置信概率值所构成的矩阵,可以表示为

u=[1,z0.9]T

(10)

因此不同置信度下POD计算模型的计算流程可以总结为:①针对无损伤情况下多次采集的导波监测信号,提取损伤指数,确定损伤指数阈值rth;②根据最小二乘法拟合损伤尺寸a与损伤指数r间的对应关系,得到未知拟合参数β0,β1,σε的点估计和区间估计;③得到POD计算模型的均值μ和标准差σ;④得到未知拟合参数β0,β1,σε的协方差矩阵Σreg;⑤得到POD计算模型的协方差矩阵Σpod;⑥得到95%置信度下不同检出率所对应的裂纹长度,绘制不同置信度下的POD曲线。

2 金属开孔结构试验验证

2.1 金属开孔结构疲劳试验方案

为验证基于信号响应分析模型的导波损伤监测技术的POD曲线测定方法的有效性,开展4件金属开孔结构疲劳裂纹损伤的导波监测试验,试验件标号依次为T1～T4。试验件为中心通孔直径为25 mm的铝合金金属结构,试验件尺寸为400 mm×168 mm×3 mm。疲劳试验过程中采用MTS液压试验机施加应力比为0.1,最大载荷为40 kN,加载频率为8 Hz的等幅拉伸循环载荷。为在疲劳试验过程中实时监测结构健康状态,在结构应力集中、易萌生疲劳裂纹的通孔两侧布置P-51型压电陶瓷传感器阵列,传感器直径为8 mm,厚度为0.45 mm。试验件与传感器布置方案,如图2所示。其中,A1-S1监测通道用于实时监测左侧裂纹的萌生和扩展情况,A2-S2监测通道用于实时监测右侧裂纹的演化情况。

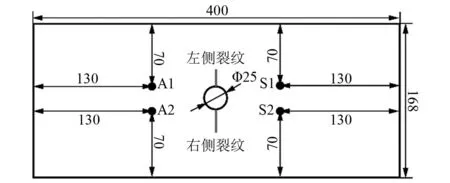
图2 开孔试验件和压电传感器布置示意图(mm)Fig.2 Schematic of center-hole specimen and piezoelectric transducers placement (mm)

开孔试验件的疲劳试验方案如图3所示。在疲劳试验过程中,疲劳裂纹的萌生和扩展情况采用离线式CCD摄像机进行测量。T1试验件在70766疲劳加载循环的真实裂纹长度如图4所示。左右两侧裂纹对A1-S1和A2-S2监测通道的无耦合影响,可通过分析单左侧裂纹和双侧裂纹时A1-S1监测通道信号证明。采用集成式结构健康监测系统进行导波监测信号的激励和接收。为了降低载荷和温度对导波监测信号的影响[24-25],将加载载荷保载至3 kN后再进行导波监测信号的采集,同时控制试验室的温度变化不超过1 ℃。选取的导波激励信号为中心频率为230 kHz的五波峰正弦激励信号,信号的采样频率为10 MHz,采样长度为4 000个数据点。

图3 开孔试验件的疲劳试验方案Fig.3 Fatigue experimental setup for center-hole specimen

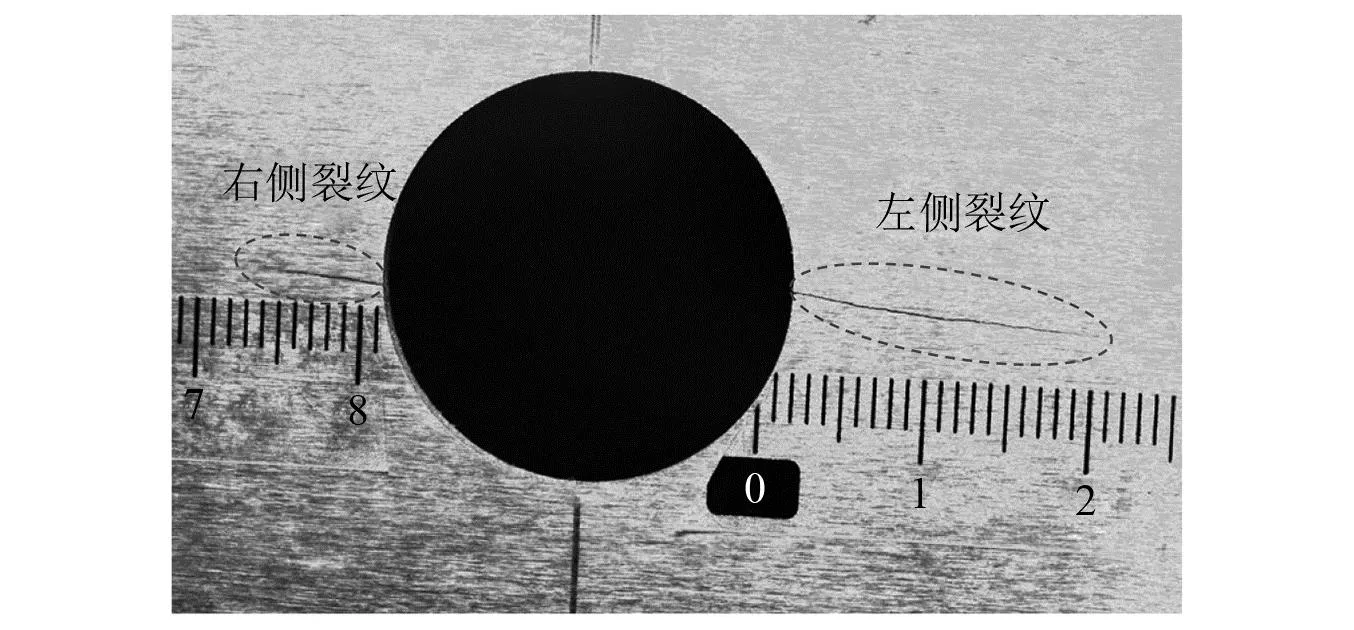
图4 70766加载循环时T1开孔试验件疲劳裂纹观测图Fig.4 Cracks observed from the microscope at 70766 load cycles for specimen T1

2.2 金属开孔结构疲劳裂纹导波监测结果及讨论

T1～T4试验件疲劳裂纹的扩展情况,如图5所示。T1试验件A1-S1通道导波信号的变化情况,如图6所示。由图6可知,随着疲劳裂纹的扩展,[8 ns, 12.5 ns]的直达波监测信号的幅值下降、相位右移。因此从幅值和相位变化的角度,提取能反映直达波波达时刻延迟和幅值变化的互相关系数(signal difference correlation coefficient,SDCC)[26]、能反映响应信号的能量变化的损伤能量比(energy damage index,EDI),以表征疲劳裂纹扩展过程中损伤监测信号的变化情况。通过选取无损伤情况下的任意一组监测信号作为基准信号,两两相互求解得到损伤指数阈值,得到T1试验件疲劳裂纹的损伤指数阈值为SDCCth=0.020 4和EDIth=0.040 9。进而利用最小二乘法得到a与SDCC、a与EDI之间的线性和对数线性对应关系,如图7所示。由图7可知:SDCC、EDI均与a具有较强的正相关性,说明损伤指数可用于表征疲劳裂纹的扩展情况;通过对比线性和对数线性函数的统计拟合优度R2,表明:相比于SDCC,a与EDI具有更强的正相关性,说明EDI对疲劳裂纹的扩展更加敏感;且相比于线性拟合,对数线性函数的拟合优度更高。

图5 T1～T4试验件的疲劳裂纹扩展情况Fig.5 Fatigue cracks growth data for specimen T1-T4

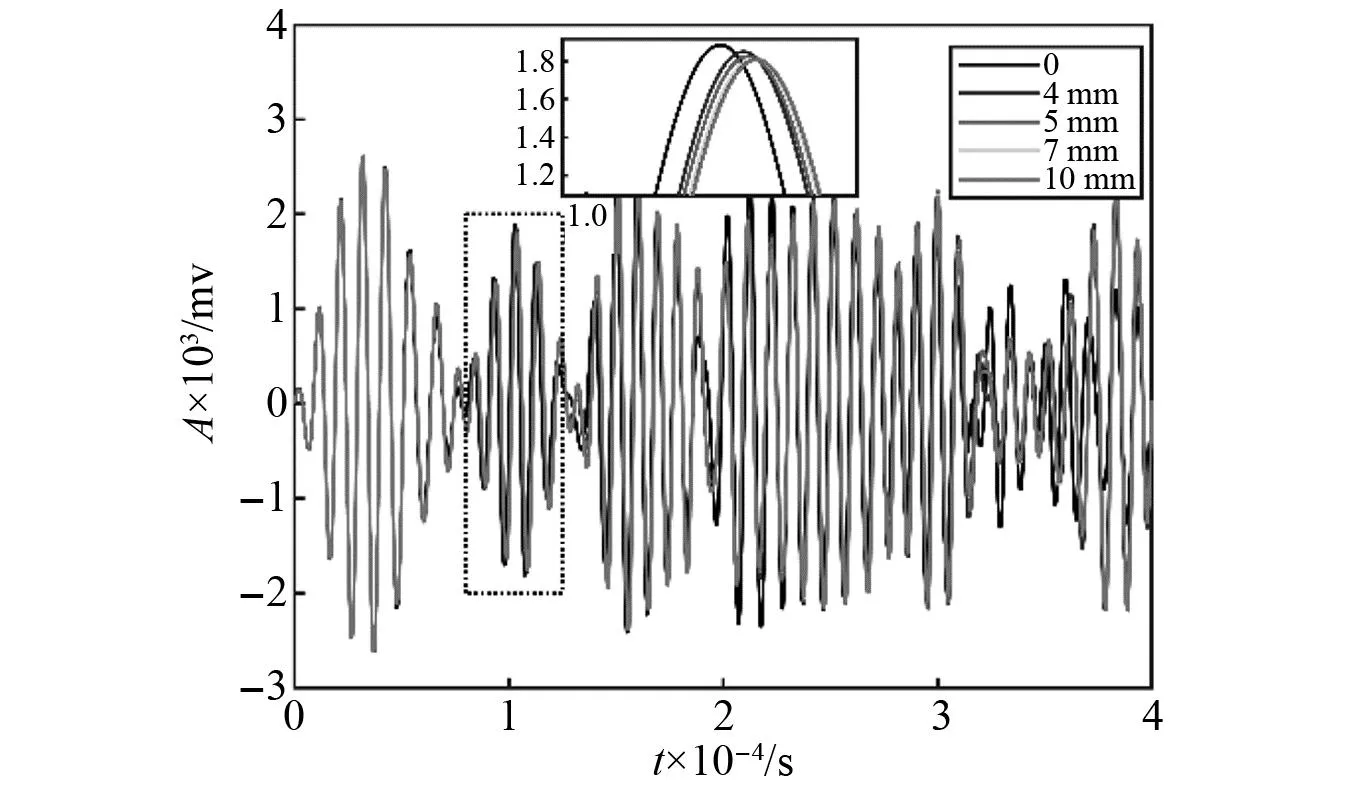
图6 T1试验件不同裂纹长度下的A1-S1通道导波监测信号Fig.6 Guided waves response signals of A1-S1 monitoring path under different crack length for specimen T1

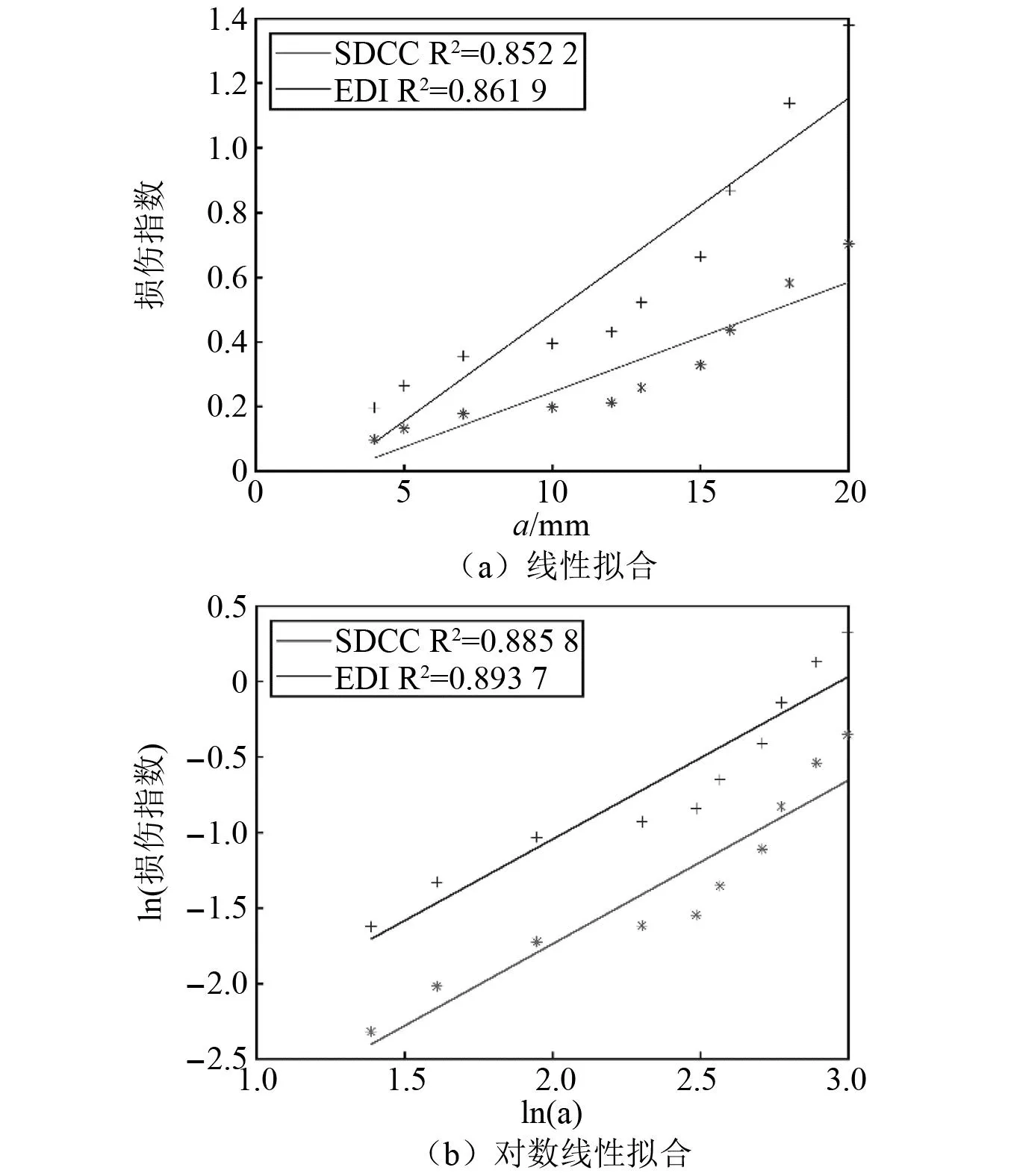
图7 T1试验件疲劳裂纹的a与SDCC、a与EDI的对应关系Fig.7 Linear fitting and logarithmic linear fitting relationship between a and SDCC、a and EDI of fatigue crack for specimen T1

由于内部因素对损伤监测能力的影响,可以采用损伤指数阈值进行表征,分别得到SDCCth取{0.020 4,0.040 4,0.060 4,0.080 4}时所对应的基于线性和对数线性拟合关系的POD曲线,如图8所示。由图8可知,针对T1试验件疲劳裂纹,在SDCCth=0.020 4时,基于线性拟合关系的POD计算模型在80%检出概率下的可检裂纹长度为5.3 mm;基于对数线性拟合关系的POD计算模型在80%检出概率下的可检裂纹长度为2.8 mm,表明基于对数线性拟合的POD计算模型具有更高的损伤监测能力;且随着损伤特征阈值的增加,同一对应关系下POD曲线逐渐向右偏移。表明随着损伤指数阈值的增加,在相同检出概率下的可检裂纹尺寸逐步增大,即其损伤监测能力和可靠性水平逐渐降低。进而对比基于线性、对数线性拟合关系的POD曲线可知,基于对数线性拟合的POD计算模型对损伤特征阈值的变化更加敏感。最后得到损伤指数阈值SDCCth等于0.020 4时,基于对数线性拟合关系的POD曲线的95%置信上下限,如图9所示。由图9可知:基于对数线性拟合的POD计算模型在95%置信上限90%检出概率下的可检裂纹长度为2.5 mm,在95%置信下限90%检出概率下的可检裂纹长度为3.4 mm,其可满足工程应用要求。

图8 不同SDCCth下T1试验件疲劳裂纹的POD曲线Fig.8 POD curves under different SDCCth of fatigue crack for specimen T1

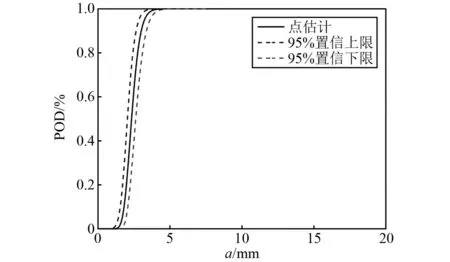
图9 T1试验件基于SDCC对数线性拟合的POD曲线的95%置信上下限Fig.9 95% confidence of POD curves based logarithmic linear fitting of SDCC for specimen T1

针对EDI损伤指数,损伤指数阈值对POD曲线的影响规律,如图10所示。对比图8和图10可知:相比于SDCC,基于EDI的线性和对数线性拟合关系的POD计算模型对损伤指数阈值的变化均较不敏感;且EDIth整体高于SDCCth,与图7中EDI值整体高于SDCC一致。在EDIth=0.040 9时,基于EDI线性拟合的POD计算模型在80%检出概率下的可检裂纹长度为5.1 mm,基于EDI对数线性拟合的POD计算模型在80%检出概率下的可检裂纹长度为1.7 mm。相比于SDCC,由于a与EDI的拟合优度更高,导致其POD计算模型在同等检出概率下的可检裂纹长度更小,说明基于EDI的POD计算模型的监测能力更强。进一步得到EDIth=0.040 9时,基于对数线性拟合的POD曲线的95%置信上下限,如图11所示。基于EDI对数线性拟合的POD计算模型,在95%置信下限90%检出概率的可检裂纹长度a90|95为2.5 mm,其相比于SDCC具有更高的损伤监测能力。

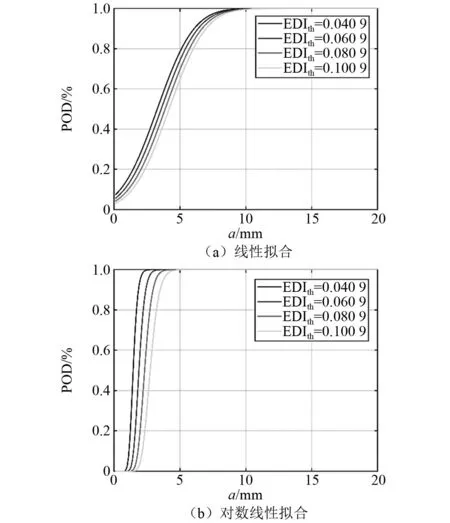
图10 不同EDIth下T1试验件疲劳裂纹的POD曲线Fig.10 POD curves under different EDIth of fatigue crack for specimen T1

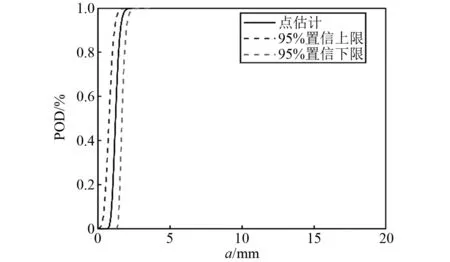
图11 T1试验件基于EDI对数线性拟合的POD曲线的95%置信上下限Fig.11 95% confidence of POD curves based logarithmic linear fitting of EDI for specimen T1

最后得到T2～T4所有试验件疲劳裂纹导波监测数据的EDIth,以及基于EDI对数线性拟合的POD曲线的95%置信上下限,如图12～图14所示。由图12～图14可知:由于试验件材料特性、传感器性能和粘贴工艺等分散性,导致各个试验件的POD曲线不同;且针对T2～T4试验件,基于a与EDI对数线性拟合的POD计算模型,在95%置信下限90%检出概率的可检裂纹长度a90|95依次为2.2 mm,3.6 mm,1.8 mm。

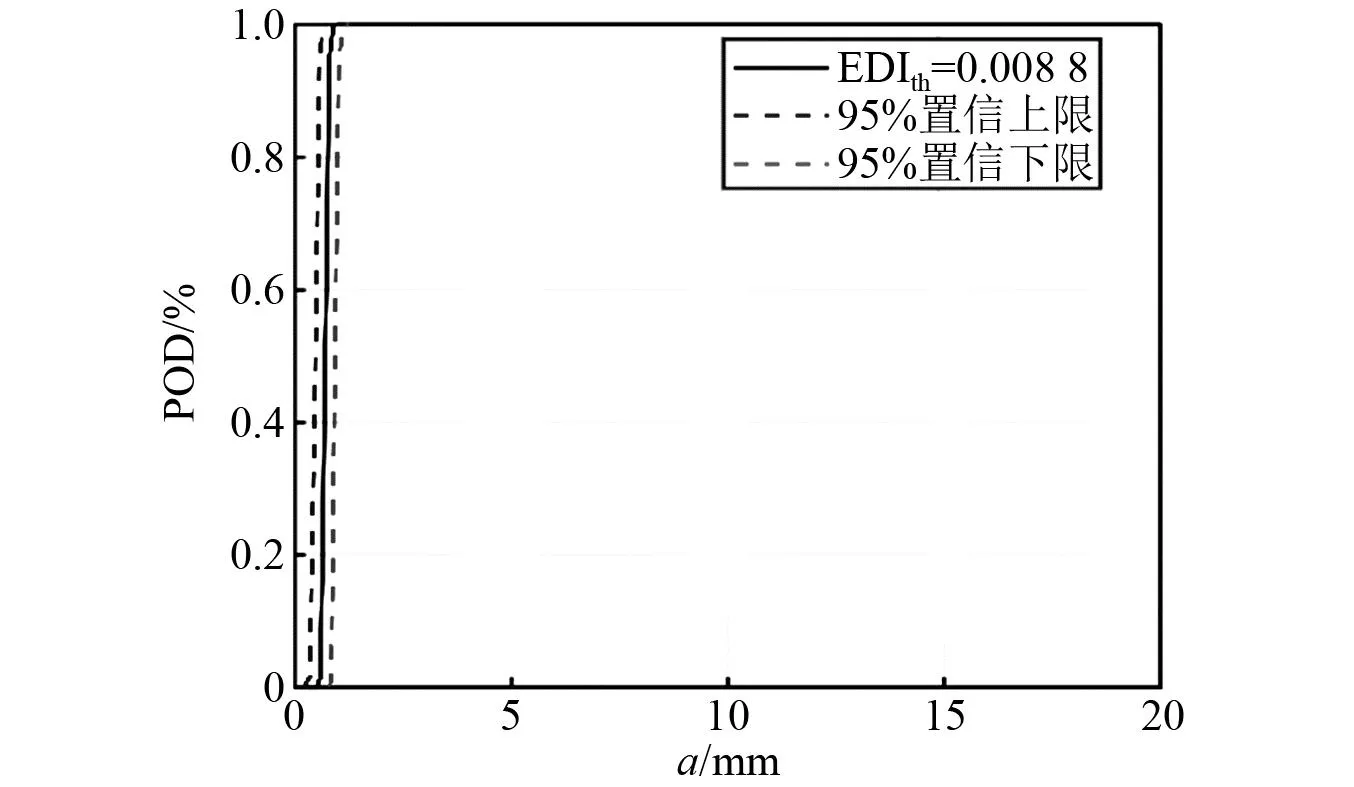
图12 T2试验件基于EDI对数线性拟合的POD曲线的95%置信上下限Fig.12 95% confidence of POD curves based logarithmic linear fitting of EDI for specimen T2

图13 T3试验件基于EDI对数线性拟合的POD曲线的95%置信上下限Fig.13 95% confidence of POD curves based logarithmic linear fitting of EDI for specimen T3

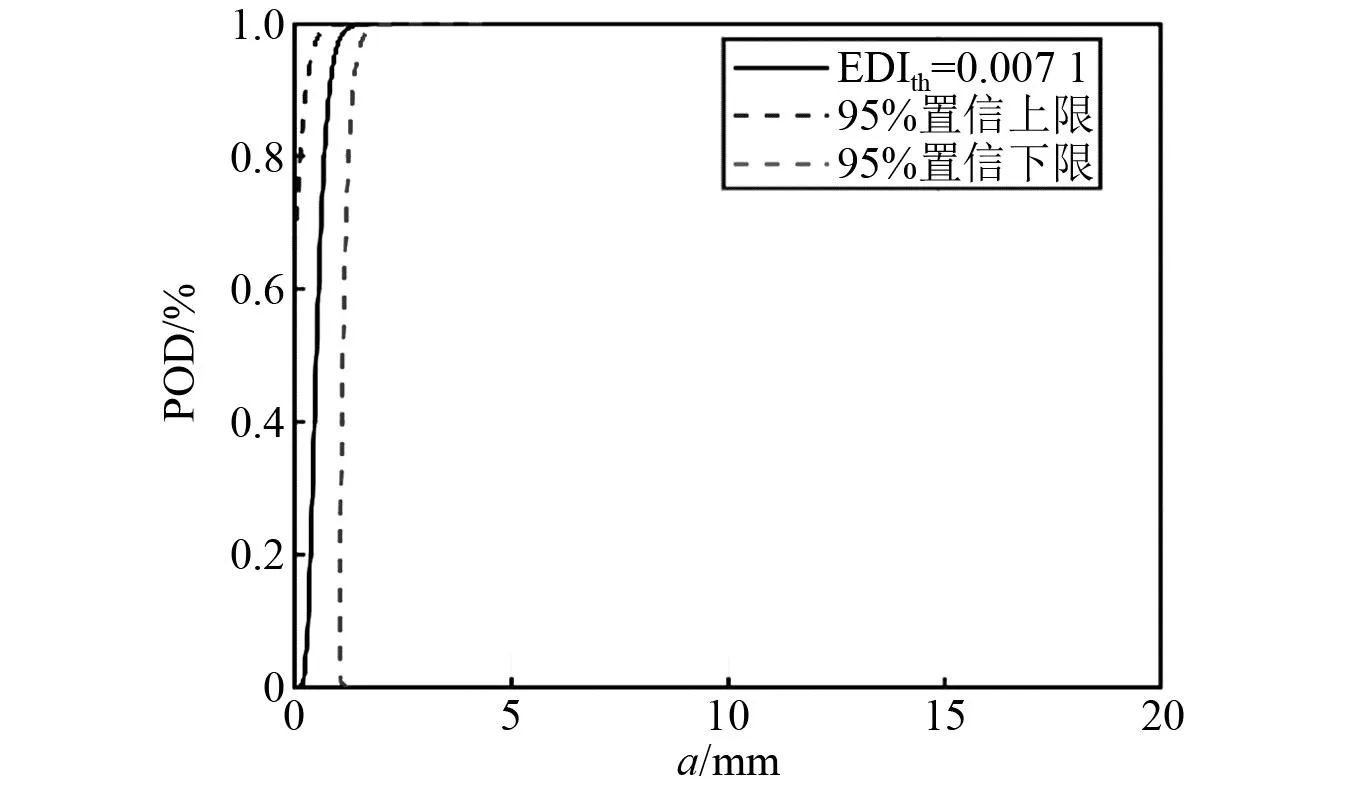
图14 T4试验件基于EDI对数线性拟合的POD曲线的95%置信上下限Fig.14 95% confidence of POD curves based logarithmic linear fitting of EDI for specimen T4

针对金属开孔结构疲劳试验件,通过提取EDI作为导波监测信号的损伤指数,采用一元对数线性函数拟合裂纹长度与损伤指数的对应关系,构建金属开孔结构裂纹导波监测的POD计算模型,其对于金属开孔结构疲劳裂纹的a90|95平均约为2.5 mm。由于金属开孔结构形式比较简单、裂纹萌生部位比较明确、试验环境条件相对理想等因素,该结构形式下损伤指数阈值较小,其对应的结构损伤监测能力和可靠性较高。因此在工程应用过程中应当尽量减小内部因素的影响,以降低损伤特征阈值。同时采用拟合度更高的函数拟合损伤尺寸与损伤指数间的对应关系。

3 金属搭接结构试验验证

3.1 金属搭接结构疲劳试验方案

开展3件金属搭接结构疲劳裂纹的导波监测试验,试验件标号依次为Q1～Q3,验证基于信号响应分析模型的结构损伤导波监测POD曲线测定方法的有效性。铝合金金属搭接结构的试验件尺寸为210 mm×100 mm×2 mm,沉头铆钉直径为8 mm。由于沉头铆钉在疲劳试验过程中无法拆卸,当疲劳裂纹在铆帽覆盖下扩展时,无法对其裂纹长度进行准确离线检测,因此为使裂纹在特定铆钉孔边扩展,在不同铆钉处预制不同长度的裂纹。疲劳试验过程中采用MTS液压试验机施加应力比为0.1,最大载荷为20 kN,加载频率为8 Hz的等幅拉伸循环载荷。为在疲劳试验过程实时监测结构健康状态,在铆钉孔两侧各布置4个P-51型压电传感器,用于监测铆钉处的结构健康状态。试验件尺寸与传感器布置方案,如图15所示。

图15 搭接试验件及压电传感器布置示意图(mm)Fig.15 Schematic of lap specimen and piezoelectric transducers placement (mm)

金属搭接结构的疲劳试验方案如图16所示。在疲劳试验过程中,疲劳裂纹的萌生和扩展情况采用离线式CCD摄像机进行测量。Q3试验件在9600疲劳加载循环的真实裂纹长度如图17所示。采用集成式结构健康监测系统进行导波监测信号的激励和接收。选取的导波激励信号为激励中心频率为170 kHz的五波峰正弦激励信号,信号的采样频率为24 MHz,采样长度为8 000个数据点。

图16 开孔试验件的疲劳试验方案Fig.16 Experimental setup for lap specimen

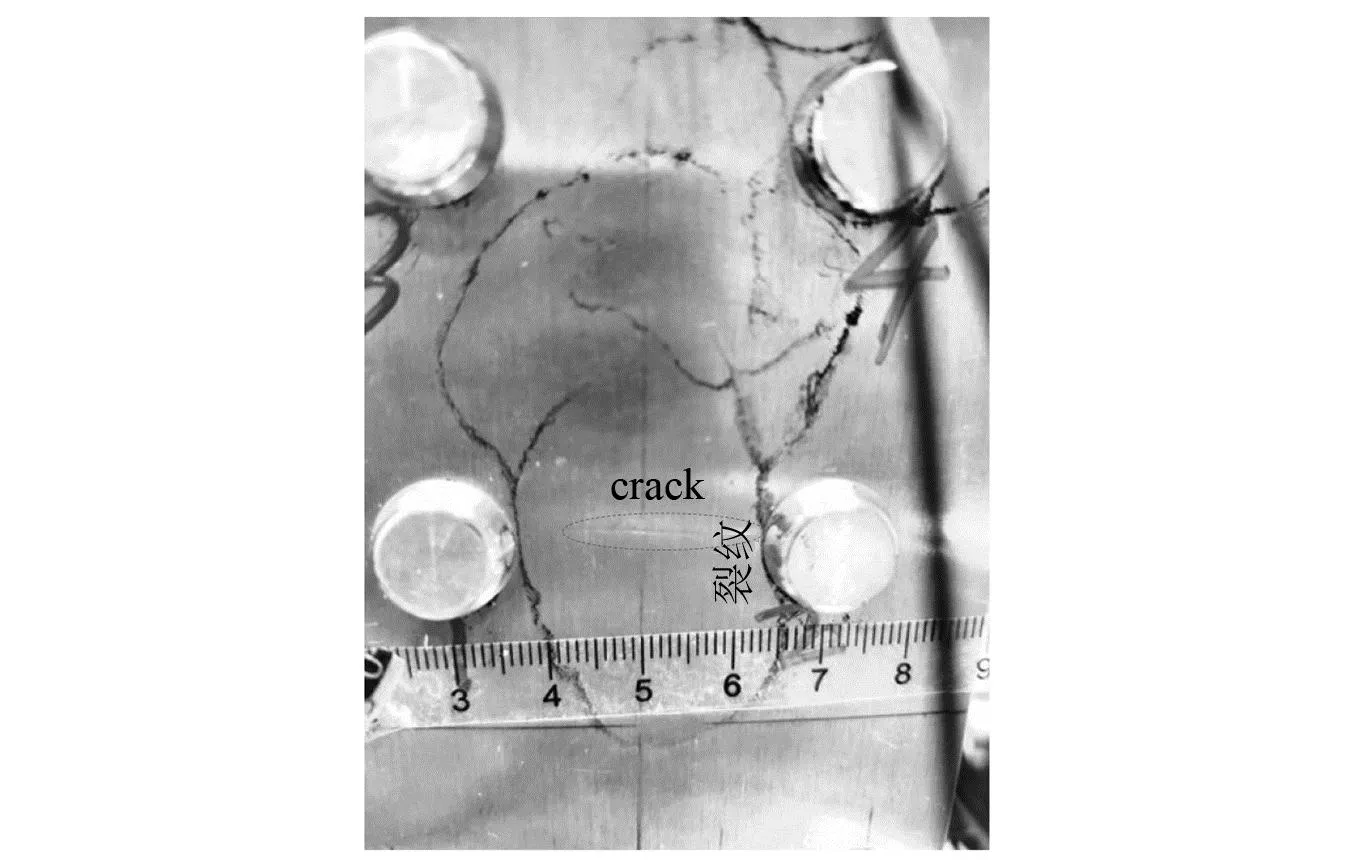
图17 9600加载循环时Q3搭接试验件疲劳裂纹观测图Fig.17 Crack observed from the microscope at 9600 load cycles for specimen Q3

3.2 金属搭接结构疲劳裂纹监测结果及讨论

图18为Q1～Q3试验件疲劳裂纹的扩展情况,其中分别根据图15所示方向在Q1试验件1号铆钉孔下侧(靠近2号铆钉孔侧),Q2试验件4号铆钉孔上侧(靠近3号铆钉孔侧),Q3试验件2号铆钉孔上侧(靠近1号铆钉孔侧)预制了4 mm初始裂纹。由图18可知,由于试验件间材料特性、加工装配工艺和传感器集成工艺的分散性,导致结构预制裂纹的初始扩展循环数存在一定的不确定性,且各个试验件的疲劳裂纹扩展历程不同。图19为Q1试验件不同裂纹长度下2-6监测通道的导波信号变化情况,选取[12 ns, 18 ns]的直达波信号段进行分析可知:疲劳裂纹的扩展会使得直达监测信号的幅值下降、相位右移。进一步分析Q1试验件预制裂纹扩展前后2-6通道导波监测信号的SDCC、EDI随a的变化情况,利用最小二乘法得到a与SDCC、EDI之间的一元线性拟合和对数线性拟合关系,如图20所示。通过对比线性拟合和对数线性拟合的统计拟合优度R2可知:两种类型的损伤指数与裂纹长度均具有较强的相关性,且对数线性拟合关系的拟合优度更高。针对Q1试验件,相比于EDI,a与SDCC的线性和对数线性的拟合关系更强。

图18 Q1～Q3试验件的疲劳裂纹扩展情况Fig.18 Fatigue cracks growth data for specimen Q1-Q3

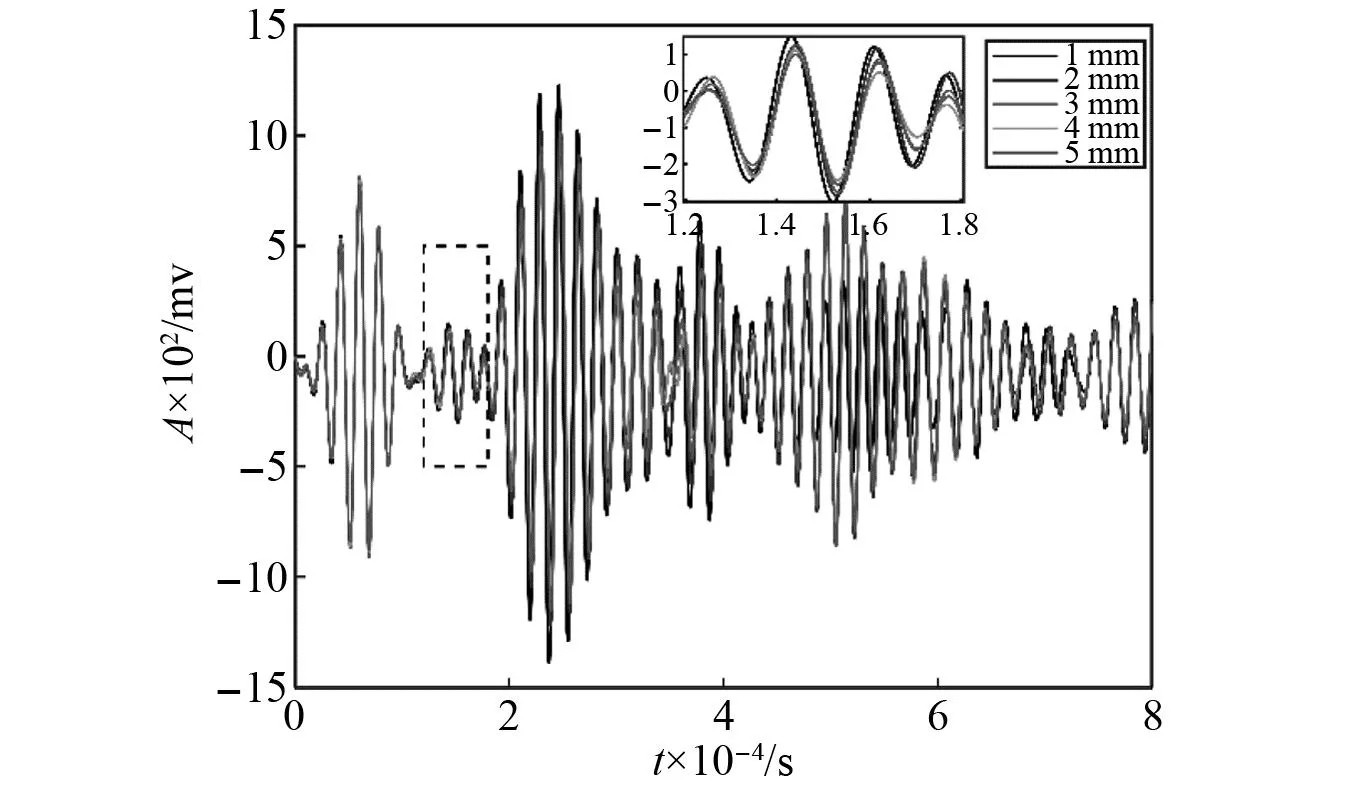
图19 Q1试验件不同裂纹长度下的2-6通道导波监测信号Fig.19 Guided waves response signals of 2-6 monitoring path under different crack length for specimen Q1

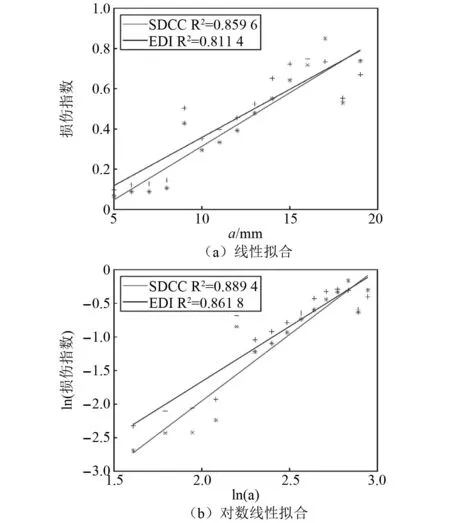
图20 Q1试验件疲劳裂纹的裂纹长度与损伤指数的对应关系Fig.20 Linear fitting and logarithmic linear fitting relationship between crack length and damage index of fatigue crack for specimen Q1

首先得到不同损伤指数阈值下,Q1试验件2-6通道基于线性拟合和对数线性拟合的POD曲线,如图21和图22所示。其中,将第一次无损伤监测信号作为基准信号,得到SDCCth=0.152 9,EDIth=0.137 5;将无损伤监测信号两两相互作为基准,得到SDCCth=0.187 3,EDIth=0.141 3。由图21可知,在SDCCth=0.152 9时基于线性拟合的POD计算模型在90%检出概率对应a=9.7 mm,基于对数线性拟合的POD模型在90%检出概率对应a=9.0 mm。由图22可知,在EDIth=0.137 5时基于线性拟合的POD计算模型在90%检出概率对应a=7.8 mm,基于对数线性拟合的POD模型在90%检出概率对应a=7.0 mm。通过对比可知,针对Q1试验件,基于EDI的POD计算模型的损伤监测能力更强,因此后续主要分析监测通道信号的EDI损伤特征值。同时表明损伤指数阈值和对应函数的拟合优度共同影响POD计算模型的检出能力。

图21 不同SDCCth下Q1试验件2-6通道的POD曲线Fig.21 POD curves under different SDCCth of 2-6 monitoring path for specimen Q1

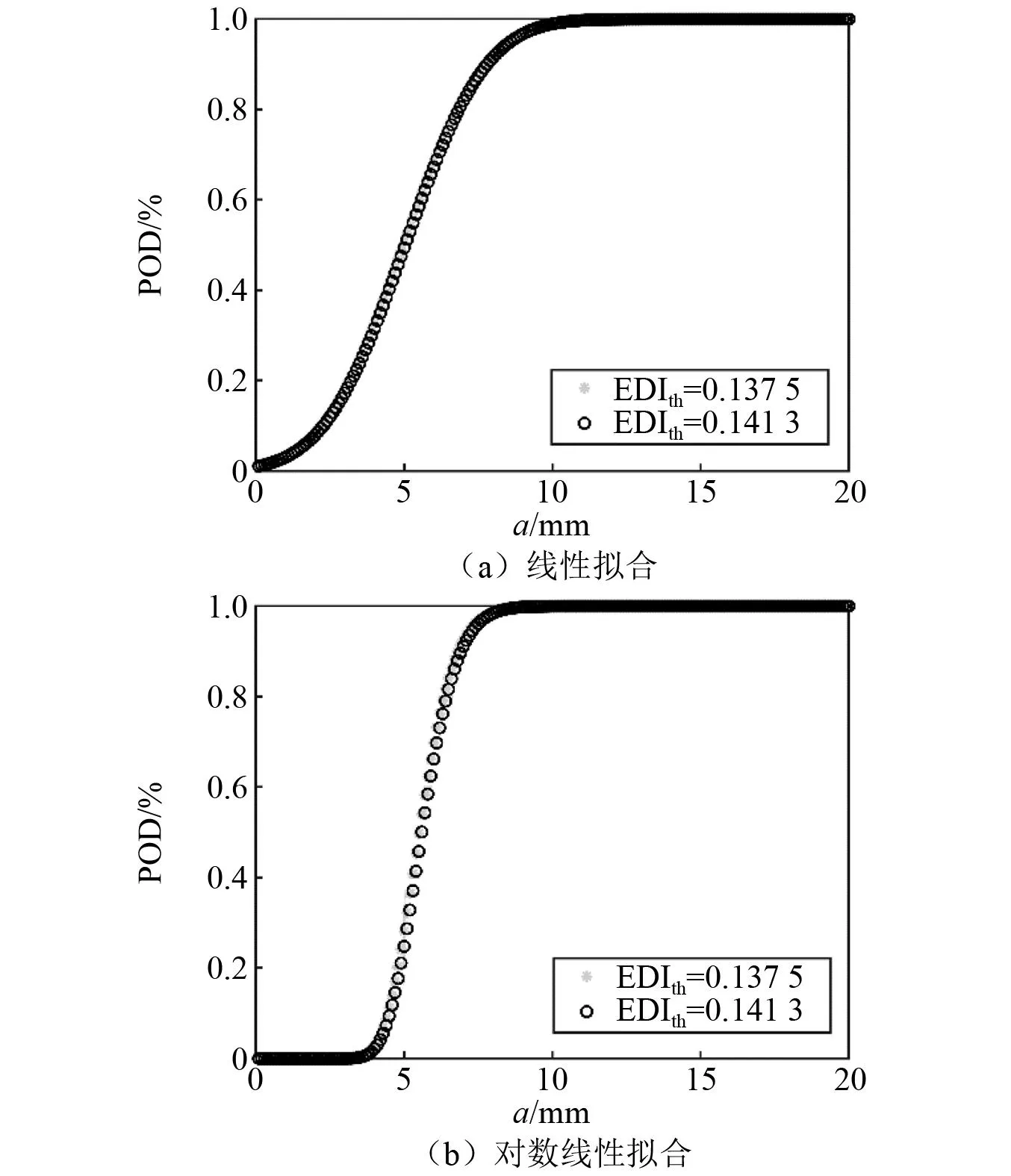
图22 不同EDIth下Q1试验件2-6通道的POD曲线Fig.22 POD curves under different EDIth of 2-6 monitoring path for specimen Q1

根据金属搭接结构传感器监测方案,当1号铆钉预制裂纹扩展时,2-6,2-7和3-7通道的导波监测信号均会发生变化。将第一次无损伤监测信号作为基准信号,得到2-7和3-7通道的EDIth分别为0.386 5,0.170 5;将无损伤监测信号两两相互作为基准,得到2-7和3-7通道的EDIth分别为0.373 5,0.207 3。图23为2-7和3-7通道在不同EDI损伤指数阈值下对应的POD计算模型。通过对比图22和图23可知,由于2-6通道在裂纹扩展的直达路径上,因此在同等裂纹长度下该通道的EDI最大,且其与a的拟合优度最高,表明其对于疲劳裂纹的扩展最敏感;相比于3-7通道,由于2-7通道与疲劳裂纹的相对距离更小,因此其对于疲劳裂纹的扩展较敏感,表现为2-7通道的EDI更大、其与a的拟合优度更高,且在同等检出概率下的可检裂纹长度更小。该结果表明:裂纹扩展直达路径上监测通道的损伤检出能力最强,且监测通道的损伤检出能力随着其距裂纹扩展路径的相对距离的增加而减小,进一步说明传感器监测方案同样对结构损伤检出概率具有影响。

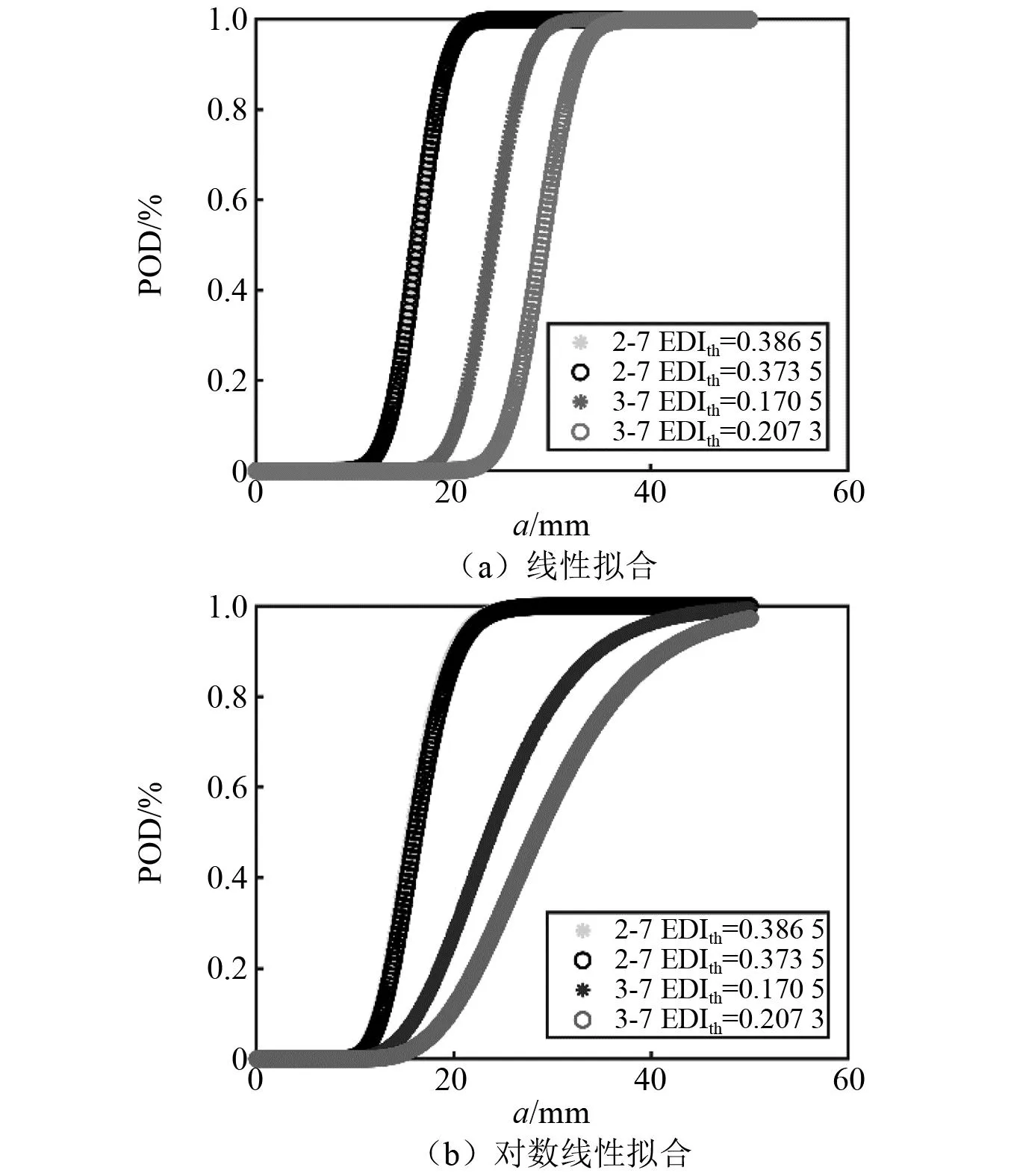
图23 Q1试验件基于EDI的2-7和3-7通道的POD曲线Fig.23 POD curves based EDI of 2-7 and 3-7 monitoring paths for specimen Q1

最后选取Q1～Q3试验件预制裂纹扩展的直达通道,分别为Q1试验件的2-6通道、Q2试验件的3-7通道、Q3试验件的3-7通道,得到基于EDI的对数线性拟合的POD曲线的95%置信上下限,如图24所示。由图可知,Q1试验件的2-6通道对应的a90|95为9.2 mm,Q2试验件的3-7通道对应的a90|95为13 mm,Q3试验件的3-7通道对应的a90|95为6.2 mm。针对金属搭接结构,基于裂纹损伤直达通道的导波监测信号的EDI对数线性拟合关系的POD计算模型所对应的平均a90|95约为9.5 mm。相比于金属开孔结构,由于连接铆钉对监测信号的传播影响,促使损伤指数阈值和损伤尺寸与损伤指数间对应关系的拟合优度发生改变,最终得到金属搭接结构损伤的导波检出能力低于金属开孔结构。

图24 Q1～Q3试验件直达通道导波监测信号的EDI对数线性对应关系的POD曲线的95%置信上下限Fig.24 95% confidence of POD curves based logarithmic linear fitting of EDI of response signals for direct paths for specimen Q1-Q3

4 结 论

本文提出了一种基于信号响应分析模型的结构损伤导波检出概率测定方法,并在金属开孔和搭接结构疲劳损伤监测试验中进行了验证,结构疲劳损伤监测试验结果表明:

(1) 针对同一通道导波监测信号,基于不同维度损伤指数的线性和对数线性对应关系的POD计算模型表征的损伤导波检出能力不一致,且损伤指数阈值和对应关系拟合函数的拟合优度耦合影响着POD计算模型。

(2) 针对同一试验件不同通道的POD计算模型,垂直于疲劳裂纹扩展路径的直达通道的POD计算模型所表征的损伤监测能力最强,且损伤监测能力随着监测通道距裂纹扩展的相对距离的增加而逐步下降。

(3) 通过分析多个金属开孔和搭接试验件的疲劳裂纹导波监测数据,得到基于EDI损伤指数与裂纹长度间对数线性对应关系的POD计算模型在95%置信下限90%检出概率的可检裂纹长度a90|95分别约为2.6 mm和9.5 mm。