变刚度地基上隔震结构群桩基础动力响应试验研究

于 旭, 单志承, 庄海洋, 陈国兴

(1.南京工程学院 建筑工程学院,南京 211167; 2. 南京工业大学 岩土工程研究所,南京 210009; 3.华东交通大学 土木建筑学院,南昌 330013)

隔震建筑以其优异的抗震性能在我国得到大量工程应用,目前已建成超过1 000万m2的隔震建筑。已有的震害调查表明:桩基的破坏是造成结构倒塌、损伤的重要原因,桩基础又是隔震结构的常用基础形式,隔震结构与基础之间设置的隔震层必将改变桩基础与上部结构的动力相互作用,进而影响上部结构和基础的地震反应特征,隔震结构桩基的抗震性能可能直接影响隔震结构的使用功能。因此,开展隔震结构桩-土共同作用体系地震响应研究对隔震结构的地震安全具有重要意义。

目前国内外学者在桩-土动力相互作用研究方面做了大量研究,取得了重要的研究成果[1-6],其中振动台模型试验是桩的地震响应以及土-桩-隔震结构动力相互作用研究的重要方法。近些年,Zhuang等[7-13]开展了不同地基上土-桩-隔震结构动力反应的振动台模型试验研究,对比分析了不同土性地基的动力反应特征、不同土性地基上隔震层的隔震效率和隔震结构动力反应规律;李昌平等[14]通过振动台模型试验研究了土-桩-高层隔震结构体系的动力反应特征,对比了刚性地基和软土地基上高层隔震结构模型的试验结果,重点分析了软土场地上高层隔震结构的动力反应特性和隔震性能;吴应雄等[15]进行了土-桩-层间隔震结构体系的振动台模型试验,对比分析远场长周期和普通地震动作用下隔震层和隔震结构的加速度和位移反应特征,探究远场长周期地震动下考虑SSI(soil-structure interaction)效应对隔震结构动力响应及减震效果的影响规律。但是,目前进行的土-桩-隔震结构动力相互作用的模型试验主要研究土-桩-隔震结构相互作用对上部隔震结构动力反应特征的影响,对隔震结构桩-土共同作用体系的地震响应缺乏深入研究,此外,已有的试验中模型地基刚度变化有限,还不能有效确定模型地基刚度与隔震结构桩基动力反应的精确关系。

已有的研究表明,饱和砂性土地基的刚度随地基动孔压比的增大而减小,而地基动孔压比的发展与地震动持时压缩比和强度密切相关[16],通过控制输入地震动持时压缩比和强度实现地基动孔压比的不同发展速度,实现间接控制地基刚度变化的目的,需要指出的是:本文的“变刚度”地基是指地基刚度在时间维度上存在变化。本文通过控制地震动持时压缩比和强度设计了饱和砂性土地基上桩基基础隔震结构振动台模型试验,有效测得了地基刚度变化过程中土体动孔压、桩基动应变、隔震结构加速度和动态位移等试验数据,限于篇幅和数据量较大,本文重点分析模型地基刚度变化对隔震结构群桩基础动力学特性的影响规律,并与不同地基中桩土共同作用系统的地震反应规律进行对比,给出了地基刚度变化过程中隔震结构群桩与土共同作用体系地震响应的变化规律,为不同场地条件下基础隔震结构的抗震设计提供重要的科学依据和保障。

1 模型试验概况

1.1 试验设备与相似比设计

本次试验在南京工业大学江苏省土木工程与防灾减灾重点实验室完成,采用的振动台设备为 MTS 单向电液伺服加载地震模拟振动台,最大载质量25 t,工作频率范围 0.1～50.0 Hz,水平向峰值加速度±1.0g。试验所用的模型土箱为层状剪切变形土箱,该模型箱的净尺寸为3.5 m(振动方向)×2.0 m(横向)×1.7 m(高度),由于该模型土箱的各层框架间可以自由的产生水平相对变形,对土的剪切变形几乎没有约束,大大减小了边界对波的反射,故能较好地模拟土的边界条件。

在土-结构动力相互作用的振动台模型试验中需通过考虑土-结构耦合的模型体系设计方法,分别对模型结构和模型地基进行相似比设计。本文模型结构选取几何长度、弹性模量和加速度为基本物理量,模型地基选取剪切模量、密度和加速度为基本物理量。根据Bukingham定理,导出其他物理量的相似比。根据已有的研究,模型地基经不同压缩比例的地震动激励后孔压发展程度不同导致模型地基刚度衰减的程度不同。因此,为控制地基刚度衰减程度,本文试验中输入地震动采用较小时间相似比压缩的地震动记录。模型体系相似关系如表1所示。

表1 模型与原型相似比Tab.1 Similarity ratio between model and prototype

1.2 模型结构与群桩基础

在综合考虑现有的试验条件、模型材料、施工工艺和相似比关系的前提下,隔震结构模型的上部结构采用4层钢框架体系,柱采用方钢管,梁采用H型钢,钢框架模型体系的尺寸如图1所示。钢框架模型纵向边长为0.8 m,横向边长为0.6 m,高为2.1 m,底层层高0.6 m,其他各层层高为0.5 m,每一层面覆盖钢板一块来模拟楼板。模型激振方向为结构纵向,结构模型的纵向高宽比为2.625,横向高宽比为3.5,结构模型高宽比符合小高宽比隔震结构的要求。上部钢框架模型质量为0.32 t。为尽可能考虑重力效应对模型结构地震响应的影响,模型每层质量为0.736 t,总质量为3.68 t。

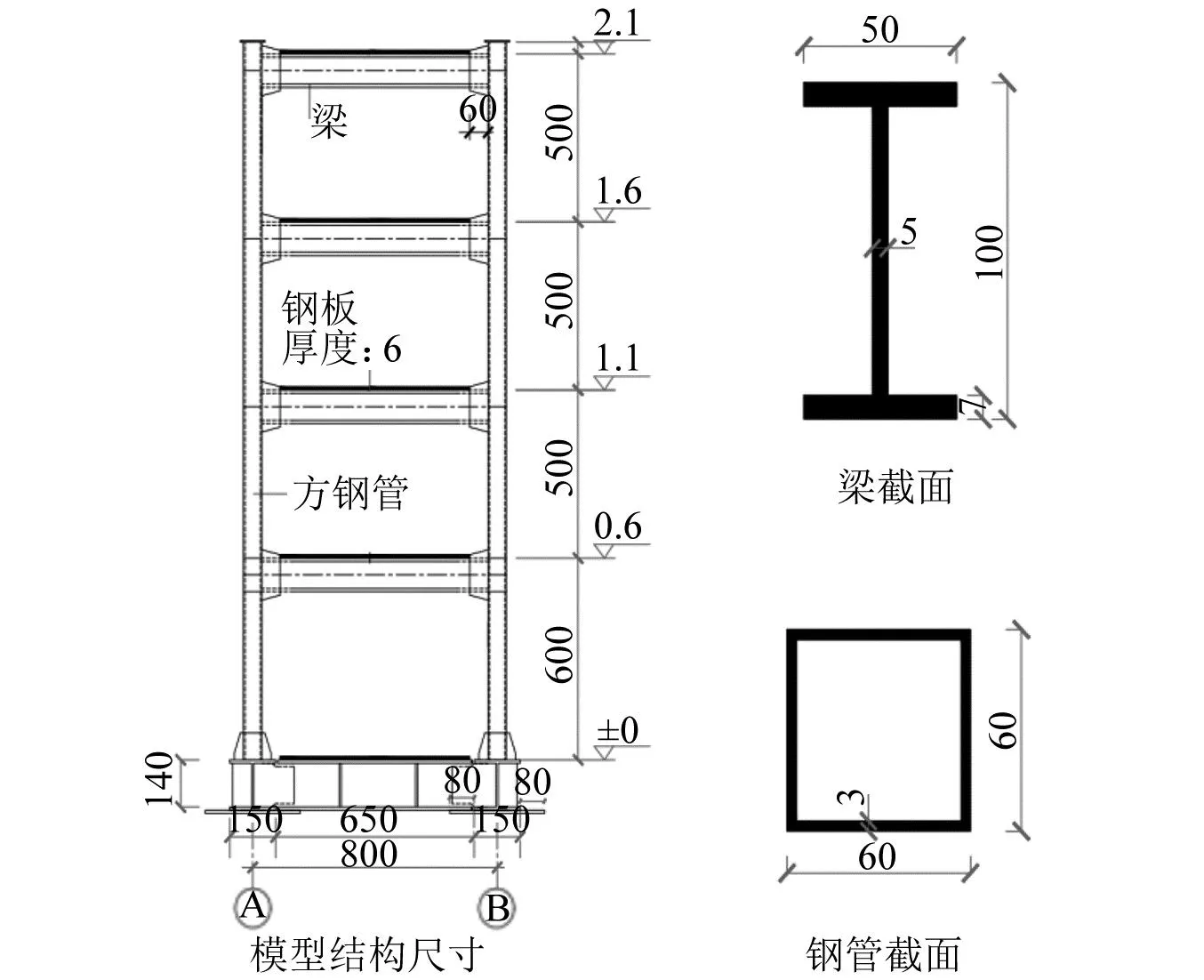
图1 钢框架模型主要尺寸(mm)Fig.1 The main dimensions of the model steel structure (mm)

根据橡胶隔震支座的应力相似比和模型结构的总质量,隔震支座采用直径为100 mm的铅芯橡胶隔震支座(隔震支座设计详见于旭的研究),隔震层共设置4个铅芯橡胶隔震支座,铅芯橡胶支座模型几何尺寸及外观如图2所示。试验前对铅芯橡胶支座进行基本力学性能试验,测得4个隔震支座平均水平刚度为0.278 kN/mm,竖向刚度为197.9 kN/mm。

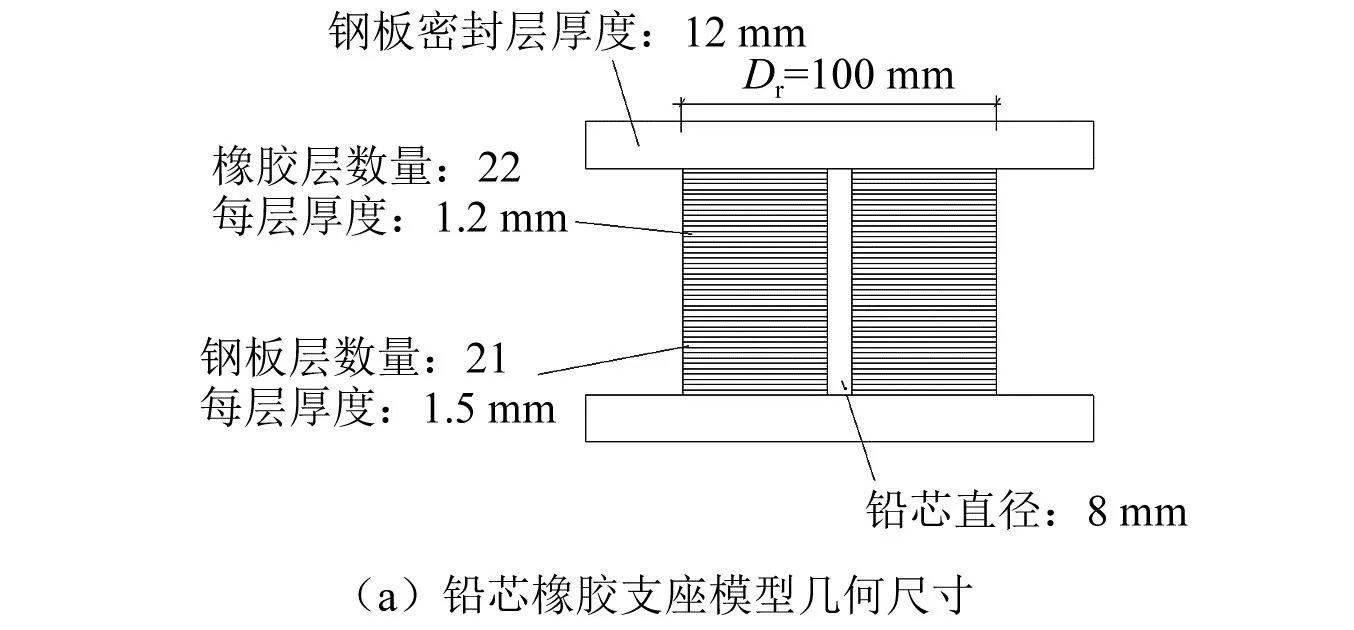
图2 铅芯橡胶支座模型Fig.2 Lead-rubber isolation bearing model

模型基础采用混凝土方桩基础,共设6根桩,桩长0.8 m,截面0.035 m×0.035 m,桩承台平面尺寸为1.2 m×1.0 m×0.1 m,承台板及桩基础配筋图如图3所示,桩位布置及桩基础模型实物图片如图4所示。

图3 承台板及桩基础配筋图(mm)Fig.3 Reinforcing bars of cushion cap and pile group foundation

图4 桩位布置及桩基础模型图(mm)Fig.4 Pile location arrangement and model of pile group foundation

1.3 模型地基

本文采用饱和砂土来制作模型地基层,在其上部覆盖一定厚度的黏土来模拟上覆不排水层,在饱和砂土层以下设置一定厚度的黏土和碎石来模型不透水层和基岩。本次试验模型地基整体尺寸为:3.5 m(长)×2.0 m(宽)×1.3 m(高),土层分为4层,自上而下设置为:100 mm厚黏土覆盖层、700 mm厚可液化的饱和松散砂土层、300 mm厚的硬黏土层、200 mm厚的碎石层。模型地基碎石层均匀平铺于模型箱底部,碎石层铺设完成后采用分层压实法铺设硬黏土层,模型地基饱和砂土层采用水沉法进行铺设,饱和砂土层完成后填筑顶部黏土层作为覆盖层,土表黏土层填筑完成后加水使土层充分饱和,模型地基装填结束静置固结2 d后抽走模型箱内多余存水。试验所用的模型土箱为南京工业大学岩土工程研究所研制的层状剪切变形土箱(如图5所示),该模型箱的净尺寸为3.5 m(振动方向)×2.0 m(横向)×1.7 m(高度),模型箱由15层矩形平面钢框架由下而上叠合,每层钢框架间放置凹槽,凹槽内放钢滚珠,形成可以自由滑动的支撑点。由于该模型土箱的各层框架间可以自由的产生水平相对变形,对土的剪切变形几乎没有约束,大大减小了边界对波的反射,故能较好地模拟土的边界条件。图5给出了模型地基及上部结构安装完成后的整体模型照片。

图5 土-桩-隔震结构相互作用体系整体模型Fig.5 Photo of overall soil-pile-isolated structure interaction model

试验前对模型地基土取样进行室内试验测定,地基表层黏土含水量30.8%～33.7%,密度1.78 g/cm3; 地基饱和砂土含水量40.5%～41.3%,密度为1.93 g/cm3,饱和砂土层细砂的粒径主要分布范围为0.075～1.000 mm,粒径小于 0.075 mm的颗粒含量为0.98%;地基下部干硬黏土含水量8.3%～9.2%,密度1.87 g/cm3。

1.4 试验测点与加载方案

根据此次振动台试验目的,需要测试模型地基土的加速度、孔隙水压力、水平位移和地表沉降,模型基础承台竖向加速度分量、水平向加速度分量、桩土界面的接触压力及桩身应变。鉴于模型体系的振动方向为模型结构纵向,本次试验沿模型体系振动方向(纵向)和垂直模型体系振动方向(横向)各设置一个观测面,传感器布置如图6所示,其中模型体系纵向为主观测面,模型体系横向为次观测面。

图6 模型体系测点布置图Fig.6 Measuring point layout of model system

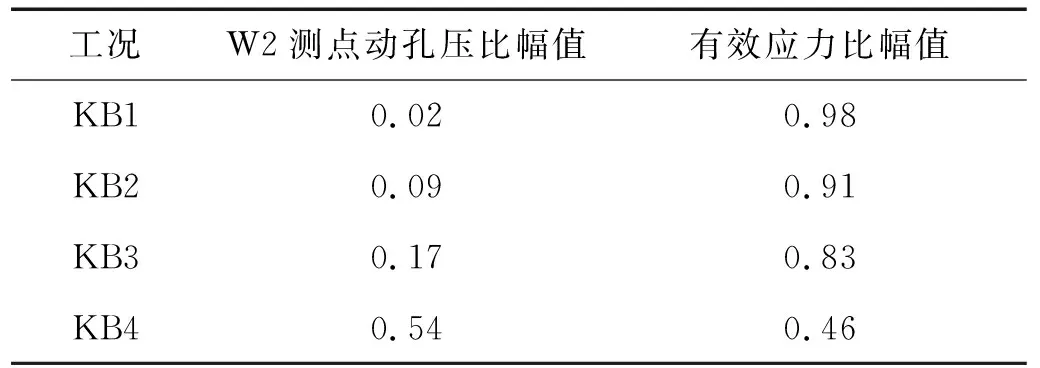
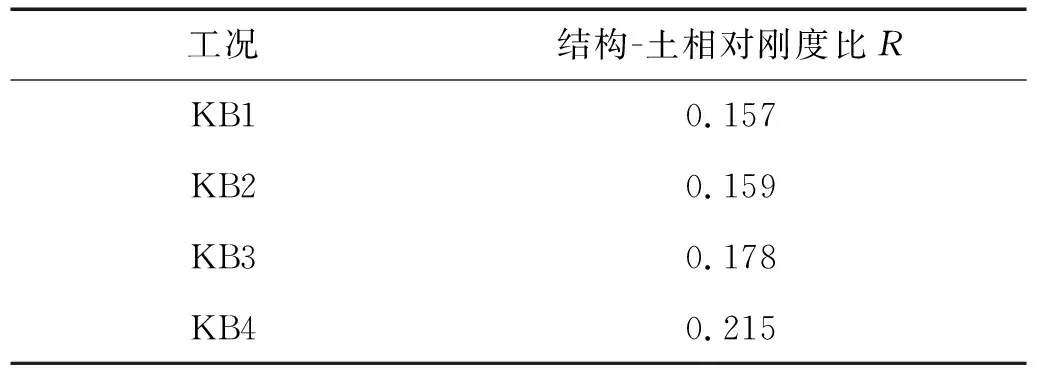
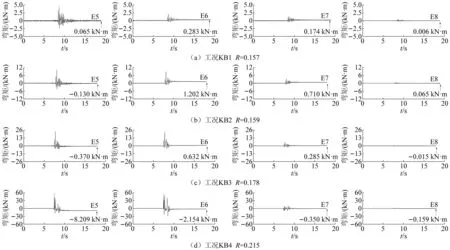
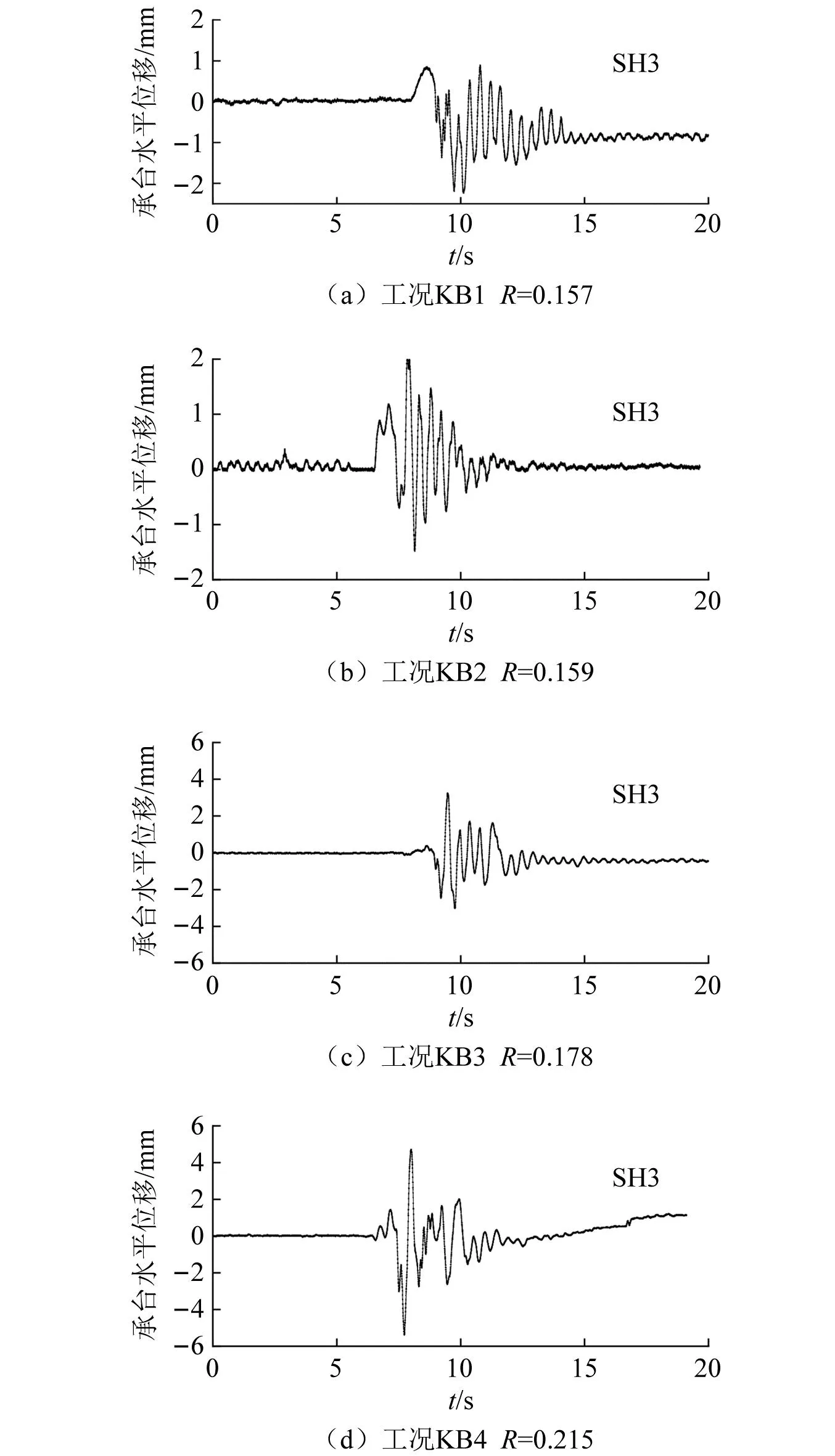
本次振动台试验仅选用Kobe波作为台面输入地震动,Kobe波为1995年日本阪神地震中神户海洋气象台记录的强震加速度记录,本试验中取其南北向的水平向加速度记录作为振动台的输入波,该地震波的原始峰值加速度为0.85g,强震部分持续时间约为10 s。根据文献[17]对于地震动的分类标准:①PGA/PGV>1.2,属于高频波;②0.8

图7 Kobe波加速度时程及傅里叶谱Fig.7 Time-history curves of acceleration and Fourier spectra of Kobe earthquake wave

为测定地基刚度变化对隔震结构模型体系动力特性参数的影响规律,试验前和每级地震动加载后采用白噪声对模型体系进行扫描,以获取模型体系的自振频率和阻尼比。试验过程中按照逐级加载的方式,基岩地震动峰值加速度(peak bedrock accelerations,PBA)分别取0.1g,0.2g,0.3g和0.5g,各加载工况之间的时间间隔不小于50 min,以保证模型地基中孔隙水压力的充分消散,具体加载方案,如表2所示。

表2 振动台试验加载工况Tab.2 Loading programs of shaking table tests

2 试验结果分析

2.1 地基动孔压比

为判定模型地基的液化状态,定义动孔压比为土体孔隙水压力与土体有效自质量应力之比值,本文采用动孔压比作为描述模型地基液化状态的无量纲参数,动孔压比能合理反映可液化模型地基的液化状态。

图8给出了不同工况时模型地基各测点的动孔压比反应时程曲线。总体来看,地基动孔压比反应随输入地震动峰值加速度的增大而增加,工况KB1和工况KB2时不同深度处各测点的动孔压比幅值基本保持在0.1以内,动孔压比反应微弱,工况KB3时孔压比反应幅值明显增加,各测点的动孔压比幅值基本保持在0.3以内,工况KB4时孔压比反应幅值显著增加,各测点的动孔压比幅值基本保持在0.6以内,已有的研究指出:在振动作用下,一般认为动孔压比达到0.8左右时土体产生初始液化,动孔压比达到1.0时土体达到完全液化。上述分析表明模型地基未达到液化状态,但地基动孔压比幅值随输入工况地震动峰值的增大而逐步增大,模型地基动孔压比发展幅度满足变刚度地基的试验设计要求。此外,不同工况下地基各测点动孔压比的变化规律基本一致,表现为模型地基不同深度测点的孔压比幅值随埋深的增加呈逐渐减小趋势,符合饱和砂性土地基动孔压比随深度变化的一般规律。

图8 不同深度处地基孔压比反应时程Fig.8 Pore pressure ratio time history in different buried depths of soil Pore pressure ratio time history in different buried depths of soil

2.2 地基刚度变化过程分析

土体的剪切模量是反映土体刚度的直接指标,由于模型试验中地基的剪切模量无法直接测量,本文采用了一种间接的确定方法,首先通过白噪声扫描测量模型地基卓越频率,根据经验公式计算出地基平均剪切波速,进而获得土体的剪切模量。场地的卓越频率与场地平均剪切波速的关系可表示为[18]

vs=4Hf

(1)

式中:vs为剪切波的传播波速;H为场地土层厚度;f为场地卓越频率 (本文利用模型地基土地表位置A12测点的数据进行谱分析求得模型地基的卓越频率)。

根据弹性理论,土体小应变剪切模量表达为

(2)

式中:vs为场地平均剪切波速;G为剪切模量;ρ为土体密度。

通过白噪声对模型体系进行扫描得到不同工况前后模型地基的卓越频率,如表3所示。根据式(1)和式(2)可计算得到模型地基的剪切模量,归一化后的地基剪切模量如表3所示。表3中G0为地基振动前的初始剪切模型。由表3可知,随输入地震动峰值的增大,模型地基剪切模量不断衰减,其中工况WN2和工况WN3时地基剪切模量衰减幅度较小,工况WN4和工况WN5时剪切模量衰减幅度明显增大,上述模型地基剪切模量的衰减规律与2.1节模型地基动孔压比的发展规律基本同步,其原因在于模型地基剪切模量随地基有效应力变化[19],而地基动孔压比的变化直接反应模型地基有效应力的变化,相应的模型地基剪切模量也发生同步变化。

表3 模型地基卓越频率和剪切模量Tab.3 Model foundation excellent frequency and shear model

为进一步分析地基剪切模量与孔压比的定量关系,定义土体有效应力比为土体有效自质量应力与孔隙水压力的差值和土体有效自质量应力之比。表4给出了不同地震动作用下模型地基饱和砂土层中部测点W2的动孔压比幅值和有效应力比幅值。

表4 地基饱和砂土层中部测点的动孔压比和有效应力比Tab.4 Dynamic pore pressure ratio and effective stress ratio of measured points in the middle of saturated sand layer of foundation

由表3和表4可以看出,模型地基饱和砂土层中部测点W2的有效应力比幅值与模型地基归一化后的地基剪切模量G/G0基本吻合,两者呈良好的正比例线性关系,上述分析结果与叶斌等人关于液化地基刚度的研究结果基本一致。根据表3和表4的结果,图9给出了本文地基饱和砂土层中部测点W2的动孔压比幅值与地基剪切模量之间的线性拟合结果,并与叶斌等实测数据的拟合结果进行对比。由图9可以看出,基于本文和叶斌等实测数据给出的归一化后的地基剪切模量G/G0与动孔压比幅值γ的线性拟合结果基本相近,均呈现出负向线性关系,说明本文采用白噪声扫描得到的地基模量衰减规律基本可靠。

图9 地基动孔压比幅值与地基剪切模量之间的关系Fig.9 Relationship between amplitude of dynamic pore pressure ratio and shear modulus of foundation

土-桩-隔震结构动力相互作用的理论研究表明,结构-土体相对刚度比能合理反映地基刚度变化对隔震结构动力特性的影响[20]。因此,为研究变刚度地基上隔震结构群桩基础的动力特性,同时验证相关理论研究成果的合理性,本文采用结构-土体相对刚度比R作为描述本文模型地基刚度变化的无量纲参数。

式中:R为结构-土体相对刚度比;TS为上部结构的固有周期;h为基础重心到第一振型相对应的惯性力重心的距离(按基本振型等效的原则计算);vs为土体的剪切波速。根据文献[21],本文模型结构固有周期TS为0.149 s,模型结构等效高度h为1.45 m,模型地基土体的剪切波速见表3。由于试验中每级工况加载后采用白噪声对模型体系进行扫描,根据式(3)可计算出每级工况加载后模型地基的结构-土体相对刚度比,如表5所示。

表5 模型地基的结构-土体相对刚度比Tab.5 First order natural frequency and damping ratio of model system on variable stiffness foundation

2.3 变刚度地基上模型地基震陷

为分析变刚度地基上模型群桩基础与地基的震陷,图10给出了不同加载工况时竖向激光位移计SV1和SV2(测点位置详见图6(b))记录的基础与地表竖向位移时程曲线。由图10可知,在输入工况为KB1、工况KB2和工况KB3时,基础承台与地表的震陷值随着输入工况加速度峰值和结构-土体相对刚度比R的增加而增加,基础承台震陷量明显高于侧向地基地表震陷量。其中:在工况KB3、R=0.178时,承台震陷量幅值为0.32 cm,地表震陷量幅值仅为0.04 cm,上述现象表明,在输入加速度峰值和结构-土体相对刚度比R小于一定限值时,地基主要发生振密现象;在工况KB4、R=0.215时,承台位移计SV1的震陷量显著增加,其震陷幅值达到1.1 cm, 地表位移计SV2的时程曲线表明,地基地表首先产生轻微的沉降位移反应,而后发生了明显的上浮位移反应,其上浮位移最大值约0.11 cm,最终稳定在0.07 cm,上述现象表明,在输入加速度峰值和结构-土体相对刚度比R大于一定限值时,基础震陷显著增加,基础下沉引起基础下方土体流向侧向地基,进而导致侧向地基受挤压而发生上浮现象,也充分说明在输入加速度峰值和结构-土体相对刚度比R大于一定限值时模型地基可能发生剪切破坏。

图10 基础与地表竖向位移反应Fig.10 Vertical displacements of foundation and lateral ground surface

2.4 变刚度地基上模型群桩基础地震反应

2.4.1 模型桩弯矩反应

本次试验沿振动方向在桩基两侧表面布置了光纤光栅,其测点编号E1～E8位置见图6(a),图6中E5-1,E6-1,E7-1和E8-1代表振动方向中间桩身上光纤光栅E5～E8测点左侧编号,E5-2,E6-2,E7-2和E8-2代表中间桩光纤光栅E5～E8测点右侧编号,因角桩的E1?E4测点应光纤光栅在同一根桩上,其中一侧测点光纤损坏,导致没有完整的应变测试数据用来计算角桩的弯矩。基于桩基各测点的实测应变,本文根据式(4)计算得出了中间桩各测点的弯矩值[22]

(4)

式中:EI为桩的抗弯刚度;d为方桩的边长;εt、εc分别为光纤光栅在桩基同一测点两侧表面(右侧和左侧)的实测应变。图11给出了变刚度地基上中间桩体各测点的弯矩反应时程曲线,本文定义使桩基右侧受拉时的弯矩为正弯矩,桩基左侧受拉时的弯矩为负弯矩。

图11 中间桩体各测点弯矩反应的时程曲线Fig.11 Time history curve of bending moment reaction at each measuring point of middle pile body

由图11的桩基弯矩反应时程表明,随着输入工况加速度峰值和结构-土体相对刚度比R的增加,中间桩体大多数测点都发生了一定程度的残余弯矩,并且桩体上部残余弯矩较大,尤其在工况KB4、R=0.215时,输入地震动主震过后桩体顶部E5测点的残余弯矩显著增大,其残余弯矩达到8.2 kN·m,试验结束后发现桩顶部E5测点位置混凝土显著开裂并有脱落现象,桩身E6测点位置混凝土亦有开裂现象,这表明在强震作用下地基刚度变化过程中桩体上部将率先进入塑性阶段,可能发生地震破坏,这种现象符合震害观测的一般规律。

图12给出了变刚度地基上中间桩体各测点弯矩幅值包络图。由图12可以看出,随着输入工况加速度峰值和结构-土体相对刚度比R的增加,中间桩体各测点弯矩幅值不断增大,尤其在工况KB4、R=0.215时,中间桩体上部弯矩幅值出现明显的骤增现象,其最大弯矩幅值出现在桩顶E5测点处,E6测点弯矩幅值略低于桩身E5测点的弯矩幅值,E7测点的弯矩幅值较E6测点弯矩幅值显著减小,桩底E8测点的弯矩幅值很小接近于0,桩体弯矩幅值自上而下呈减小的趋势。上述分析表明:强震下变刚度地基上桩体上部弯矩幅值较大,易产生地震破坏,而桩体下部弯矩幅值较小。

图12 变刚度地基上中间桩体各测点弯矩幅值包络线Fig.12 Bending moment amplitudes of the middle pile at each measurement point on variable stiffness Foundation

基于上述的测试结果分析,造成变刚度地基上桩基上部弯矩幅值大幅增加的原因可作如下解释:在地震作用下隔震结构在基础顶面产生较大的弯矩和轴力,其主要由基础承台和桩基共同承担,然而结构-土体相对刚度比R随输入工况地震动峰值的增大而增大,模型地基刚度降低,这导致承台底面地基反力减小,基础承台震陷增加,原本由基础承台承担的弯矩和轴力向桩基础转移,导致桩基上部弯矩和轴力增大,此外,由于地基刚度降低基础承台发生显著的转动反应,隔震结构随基础承台摇摆产生的二阶效应将导致桩基上部弯矩进一步增加;由此可见,在地基刚度变化过程中隔震结构基础承台震陷与基础承台强烈转动反应的共同作用可能是导致桩基上部弯矩骤增的主因。

2.4.2 模型桩顶位移反应

本次试验中在模型基础承台顶部布置了水平激光位移计SH3(测点位置详见图6(a))测试承台水平位移,由于承台水平刚度较大,承台的运动可视为刚体运动,桩顶位移可通过承台顶SH3测点的实测位移获得,图13给出了不同工况下桩顶位移时程曲线。由图13可以看出,随输入工况地震动峰值以及结构-土体相对刚度比R的增大,桩顶水平位移明显增大,其中在工况KB1、R=0.157和工况KB2、R=0.159时桩顶位移幅值相对较小,位移幅值为分别为1.63 mm和2.89 mm;在工况KB3、R=0.178和工况KB4、R=0.215时,桩顶位移幅值明显增大,桩顶位移幅值达到4.84 mm和7.4 mm。地基刚度变化过程中桩顶水平位移幅值明显增大的原因可作如下解释:变刚度地基上地基刚度随输入工况加速度峰值的增大而降低,地基土性逐步变软,导致基础承台及桩侧侧移阻力逐渐减小,同时地基土性变软使地基侧向扩展变形增大,两者共同作用下使桩顶水平位移显著增大。值得注意的是在工况KB4、R=0.215时,主震后桩基水平位移出现明显的单边累积水平位移,结合试验后模型基础的实际情况,这说明在强震作用下地基刚度变化过程中桩基上部率先出现明显的残余弯曲变形,桩基上部可能发生地震破坏,这与2.4.1节的分析结果相吻合。

图13 桩顶水平位移时程曲线Fig.13 Time history curves of the horizontal displacement at the top of pile

2.4.3 桩基承台转动反应

(5)

表6 变刚度地基上基础转动角加速度反应峰值Tab.6 Rotation angular acceleration peak of the pile foundation on variable stiffness foundation

根据2.4.3节分析可知:强震下结构-土体相对刚度比越大,隔震结构基础转动效应越显著,其必然增大下部桩顶的动弯矩反应幅值。因此,有必要进一步分析结构-土体相对刚度比和输入地震动峰值对隔震结构基础转动效应的影响规律,基于本文的试验结果以及本文作者已完成的刚性地基、硬土地基和软土地基上隔震结构模型体系振动台试验的结果,同时考虑到已完成的模型试验中以Kobe波激振时隔震结构地震反应最为强烈,图14给出了Kobe波激振时不同地震动强度下隔震结构基础转动角加速度峰值与结构-土体相对刚度比R的关系,图中PGA为隔震结构模型基底输入加速度峰值。需要说明的是,为对比图14中4种地基上隔震结构基础的转动角加速度峰值,本文参照Zhang等的二次插值法基于试验实测数据计算得到不同地基上隔震结构基础转动角加速度峰值以及结构-土体相对刚度比,使其对应的基底输入加速度峰值分别为0.1g,0.3g和0.5g,使隔震结构模型在不同地基上具有等效的基底加速度峰值。由图14可以看出:在PGA=0.1g且场地条件(0.050.1)时隔震结构基础转动角加速度峰值的增长幅度明显增大;尤其是在PGA=0.5g且场地条件(R>0.21)时隔震结构基础转动角加速度峰值增长幅度更为显著,隔震结构基础转动角加速度峰值超过1.6 rad·s-2,上述分析表明,当输入地震动强度PGA和结构-土体相对刚度比R达到一定量值时,隔震结构基础将出现剧烈的转动反应,其原因可能与土-桩-隔震结构动力相互作用相关。

图14 隔震结构基础转动角加速度峰值与结构-土体相对刚度比R的关系(Kobe波)Fig.14 Relationship between the peak of rotational angular acceleration and the relative stiffness ratio R of structure-soil of isolated structure (kobe wave)

由于隔震结构基础转动角加速度峰值随结构-土体相对刚度比的增大总体上均呈增长趋势。图14分别给出了不同PGA作用下隔震结构基础转动角加速度峰值与结构-土体相对刚度比R的指数拟合公式,可以看出隔震结构基础转动角加速度的指数预测公式在PGA≤0.3g时的拟合效果较好但在PGA=0.5g时的拟合效果相对较差,上述发现还有待于通过数值模拟和理论分析进一步验证。

3 结 论

本文通过控制地震动持时压缩比和强度的方法设计了变刚度地基上桩基基础隔震结构振动台试验,研究了变刚度地基上隔震结构群桩基础的动力反应特征,揭示了地基刚度变化对隔震结构群桩基础动力学特性的影响规律,得到的主要结论如下:

(1)在输入加速度峰值和结构-土体相对刚度比R小于一定限值时,隔震结构群桩基础和侧向地基地表均发生下沉,主要与地基土层的振密有关,在输入加速度峰值和结构-土体相对刚度比R大于一定限值时,群桩基础震陷显著增加,侧向地基地表隆起,其主因与模型地基发生剪切破坏有关。

(2)变刚度地基上结构-土体相对刚度比和输入地震动强度显著影响隔震结构群桩基础弯矩反应,强震下结构-土体相对刚度比越大,隔震结构群桩基础中间桩体上部弯矩反应幅值增大越显著,而中间桩体下部弯矩幅值较小,中间桩体上部弯矩幅值骤增可能是地基刚度变化过程中基础承台震陷与基础承台强烈转动反应共同作用的结果。

(3)随输入地震动峰值以及结构-土体相对刚度比R的增大,隔震结构群桩基础桩顶水平位移明显增大,在输入加速度峰值和结构-土体相对刚度比R达到一定量值时,群桩基础桩顶水平位移在主震后出现明显的单边累积水平位移,桩基上部可能发生地震破坏。

(4)不同地基上隔震结构基础转动角加速度峰值以及结构-土体相对刚度比的关系表明,当输入地震动强度和结构-土体相对刚度比达到一定量值时,隔震结构群桩基础承台将出现剧烈的转动反应,主要原因与土-桩-隔震结构动力相互作用有关,上述发现还有待于通过数值模拟和理论分析进一步验证。