基于无模型自适应控制的半潜式平台运动性能研究

余 杨, 张鹏辉, 成司元, 张文豪, 余建星

(1. 天津大学 水利工程仿真与安全国家重点实验室,天津 300072; 2. 天津大学 天津市港口与海洋工程重点实验室,天津 300072)

随着陆地油气资源开发日益枯竭,越来越多人把目光由陆地转向海洋。南海作为我国最大的海,有着约58万亿m3天然气及290亿t石油储量[1],油气资源极其丰富,大部分油气储量集中在深海。作为深海浮式生产平台中的一种,半潜式平台由坐底式平台发展而来,平台甲板与下浮体之间用立柱连接,具有水线面小、波浪运动响应小、适应恶劣海况、工作水深范围大、甲板面积大和移位灵活等优点,常常被用于深海油气资源的开发。

南海自然环境条件极其复杂,定位系统失效不可避免地会出现。半潜式平台想要维持在固定海域工作, 必须拥有良好的定位系统,以便与恶劣的自然环境条件相抗争。关于半潜式平台定位系统失效及其运动响应,国内外相关学者进行了诸多研究。Zhu等[2]应用时域仿真程序,分析了单缆失效情况对装配DP辅助系泊系统半潜式平台的平台运动、推进器功率消耗和系泊绳张力的影响。Yang等[3]使用SESAM软件建立半潜式平台及其动力定位系统模型,进行时域仿真模拟,并与深水水池模型试验结果对比,给出了平台在完整工况与推进器部分失效状况时的运动响应与动力定位能力。Liang等[4]提出了一种完全耦合的六自由度非线性动力学模型,用于分析装备有DP系统的半潜式平台的动力响应。Liang等[5]还采用Cummins方程,用状态空间模型代替方程中的卷积项,直接设计出一种DP控制策略,模拟时域上的响应。Hassani等[6]提出了一种基于动态假设检验的方法,实现在没有测量系泊索张力的情况下,及时检测推力器辅助系泊系统的系泊索断裂情况,适当使用DP推进器的援助以弥补失去的张力,避免系泊索的连续断裂。Blanke等[7]以推进器辅助的系泊系统为例,开展复杂自动化系统的容错分析和设计,并通过一个船舶模型,讨论了船舶定位控制系统的容错控制,特别是位置系泊的容错控制,提出了一种允许在单一和多重故障情况下评估安全位置的系泊控制方法。Cheng等[8]利用AQWA软件二次开发功能,研究了半潜式平台在表面波载荷和内孤立波载荷联合作用下的动力响应,分析了系泊失效对其影响。朱航等[9]通过时域方法分析了HYSY-981半潜式平台在风浪联合作用下的非线性运动响应,得到其运动响应时程曲线和位移的功率谱密度曲线。

现代科学技术的发展和完善导致所建立系统模型的非线性越来越复杂,想要获得简单且精准的数学模型来实现控制器设计变得越来越难。数据驱动控制(data driven control, DDC)可以在模型参数未知的情况下,利用离线或在线的过程数据直接进行控制器设计,实现对过程的有效控制[10]。作为数据驱动控制方法的一种,无模型自适应控制(model free adaptive control, MFAC)最早由侯忠生[11]于1994年在其博士论文中提出,用于解决一般离散时间非线性系统的控制问题。随后,相关学者进行了大量研究,并将其整理成册,形成了较为完善的无模型自适应控制理论。近些年来,无模型自适应控制在理论不断完善的同时,也广泛应用在运动控制、工业过程控制、交通控制和网络控制等领域。Treesatayapun等[12]将无模型自适应控制应用于有刷直流电机控制系统中,得到了比传统控制方法更小的跟踪误差。Ren等[13]将无模型自适应控制与迭代学习相结合,应用于交通网络控制中,获得了更好的容错性。Yuan等[14]将基于RISE和ISMC的无模型自适应控制应用于四旋翼飞行器编队轨迹追踪问题,取得了较高的控制精度、稳定性和鲁棒性。Sourni等[15]将自适应最优控制器应用于结构地震运动控制中,有效地减小了地震过程中的动力响应。任丽娜等[16]将无模型自适应控制应用于气动加载系统压力跟踪控制中,与经典比例-积分-微分(proportional-integral-derivative, PID)进行仿真比较,具有较强的适应性和鲁棒性。在船舶与海洋工程领域,无模型自适应控制主要应用于船舶减摇运动控制中。宋杨等[17]基于多新息理论、跟踪微分器技术和混沌遗传优化算法,对无模型自适应控制进行改进,并应用于船舶减摇运动控制系统中,验证了改进方法的有效性和实用性。杨太阳[18]通过建立船舶运动数学模型,将MFAC应用于减摇控制中,表现出更强的自适应能力、鲁棒性和适应性。作为运动控制中的一种,半潜式平台动力定位控制系统主要是通过测量出来的平台位置和艏向,来计算平台维持在固定海域及保持自身艏向所需要的作用力。虽然目前暂未有学者将无模型自适应控制作为动力定位系统控制理论,但在以上各个领域,特别是运动控制中的成功应用也从侧面反映了该方法在动力定位控制系统中的有效性。

本文以一艘工作在我国南海海域的半潜式平台为研究对象,利用AQWA软件进行水动力计算分析。研究首次将无模型自适应控制作为动力定位系统控制理论,进而通过动力定位系统来弥补半潜式平台在系泊失效后的运动响应,减小系泊失效对半潜式平台带来的危害。其中,控制力和力矩的施加是通过Fortran语言来编译动态链接库,从而达到二次开发的功能来实现的。其研究流程大致如下。首先,建立半潜式平台模型,对频域计算结果进行比对以验证模型的正确性;然后,进行时域计算分析,以探究系泊失效前后半潜式平台运动响应变化;最后,将无模型自适应控制作为动力定位系统控制理论,对半潜式平台在系泊失效后的运动响应进行控制,并对三种动态线性化方法下的无模型自适应控制的控制效果进行比较。

1 计算理论基础

1.1 三维势流理论

假设流体是无黏无旋、不可压缩均匀流体,且波幅或波高相对于波长是无限小的。在线性波理论下,根据线性叠加原理,当浮体与波浪相互作用时,速度势φ可分解为

φ(x,y,z,t)=φI(x,y,z,t)+φD(x,y,z,t)+
φR(x,y,z,t)

(1)

式中,入射势φI是已知的。只需要求出绕射势φD和辐射势φR,就可以得到速度势φ。

此时,采用三维源分布法即边界元法进行求解。三维源分布法将结构物湿表面上的某点M(ξ,η,ζ)视为具有单位强度的点波源,对波动场任意一点q(x,y,z)所引起的扰动势(源势)为G(x,y,z;ξ,η,ζ),则点q(x,y,z)的绕射(或辐射)势为

(2)

式中:f(ξ,η,ζ)为源强度分布函数,可以由物面边界条件得到;G(x,y,z;ξ,η,ζ)为格林函数。

在计算得到扰动后波动场内任一点总速度势φ后,应用线性化的伯努利方程便可得到结构物表面S上的波压强p分布。将波压强p沿结构物表面S积分,可得到作用在结构物上的总波力FWave和总波力矩MWave分别为

FWave=-ρω∬SRez[i(φI+φS)e-iωt]ndS

(3)

MWave=-ρω∬SRez[i(φI+φS)e-iωt](r×n)dS

(4)

式中:Rez[]为取复数表达式的实部;n为结构物表面S上某点的单位外法向矢量;r为结构物表面S上某点到取到力矩那点的径向矢量[19]。

1.2 莫里森方程

在计算小尺度结构物所受波浪力时,常常采用以绕流理论为基础的半理论半经验公式——莫里森方程。其表达式为

(5)

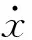
1.3 时域运动方程

浮式结构物的时域运动方程可以用卷积积分的形式表示为

(6)

式中:m为结构物的质量矩阵;A∞为无限频率下的流体附加质量矩阵;C为由于绕射单元产生的除了线性辐射阻尼外的阻尼矩阵;K为总体刚度矩阵;F(t)为结构物所受外力,包括一阶波浪力、二阶波浪力、流力、风力、系泊力和推进器推力;h为加速度脉冲函数矩阵,可表示为

(7)

式中:A(ω)为附加质量矩阵;B(ω)为流体动力阻尼矩阵。

1.4 系泊系统分析方法

在进行系泊系统与结构物的耦合分析时,所采用的系泊系统分析方法为集中质量法。集中质量法将系泊缆离散成设定段数,每段系泊缆的质量集中均分在两端节点上,中间用无质量弹簧连接。最终,系泊缆就可以看作由相应质点和无质量弹簧组成的质量——弹簧系统。

系泊缆单元受力示意图如图1所示。

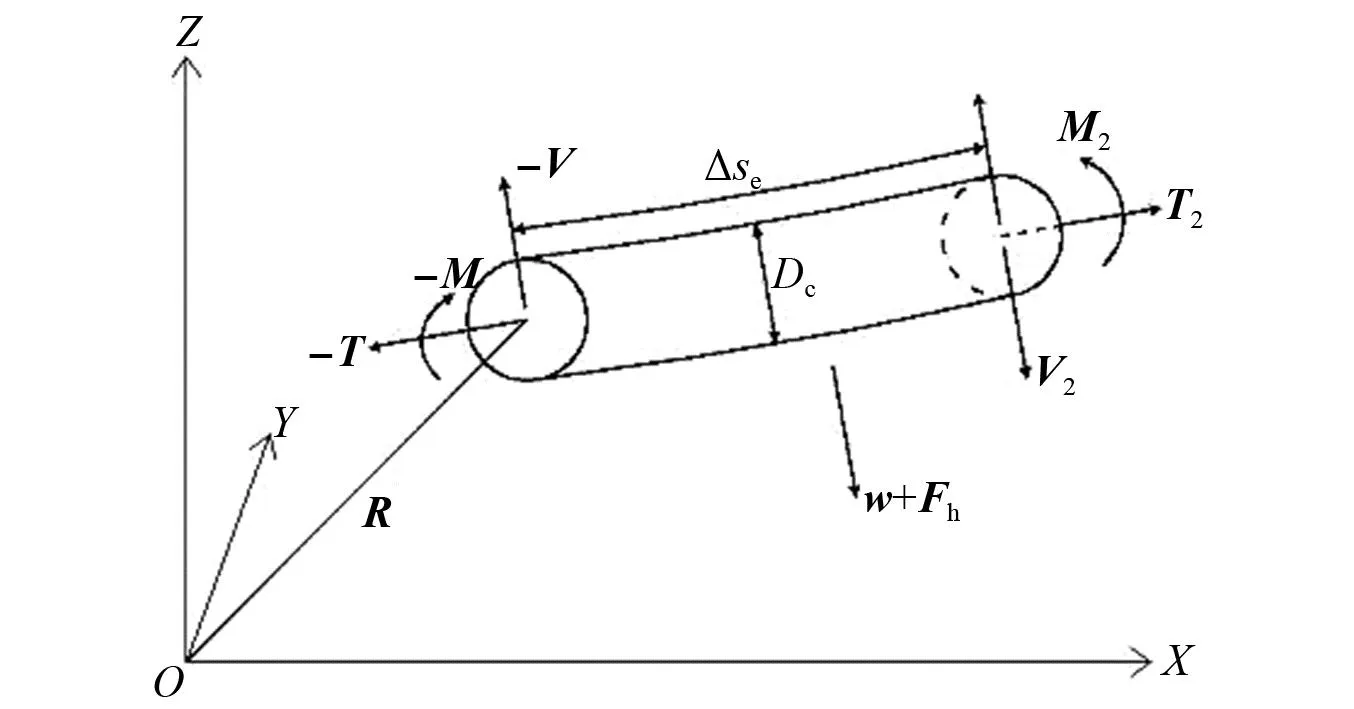
图1 系泊缆单元受力示意图Fig.1 Force on a cable element

其运动方程可表示为

(8)

(9)

式中:m为系泊缆单位长度质量;q为单位长度分布力矩载荷;R为单元第一个节点的位置矢量; Δse为单元长度;w为单元质量;Fh为单位长度外部水动力载荷;T为单元第一个节点上的张力;M为单元第一个节点上的弯矩;V为单元第一个节点上的剪力。

2 半潜式平台模型的建立及验证

2.1 半潜式平台主体模型的建立

本文以我国南海海域一艘新型半潜式平台为研究对象,其配备有悬链式系泊系统。同时,在浮体底部装备有DP-3动力定位系统。该平台工作水深为1 500 m,最大钻井深度可达10 000 m,兼具勘探、钻井、完井和修井等作业功能。其模型参数[20]如表1所示。

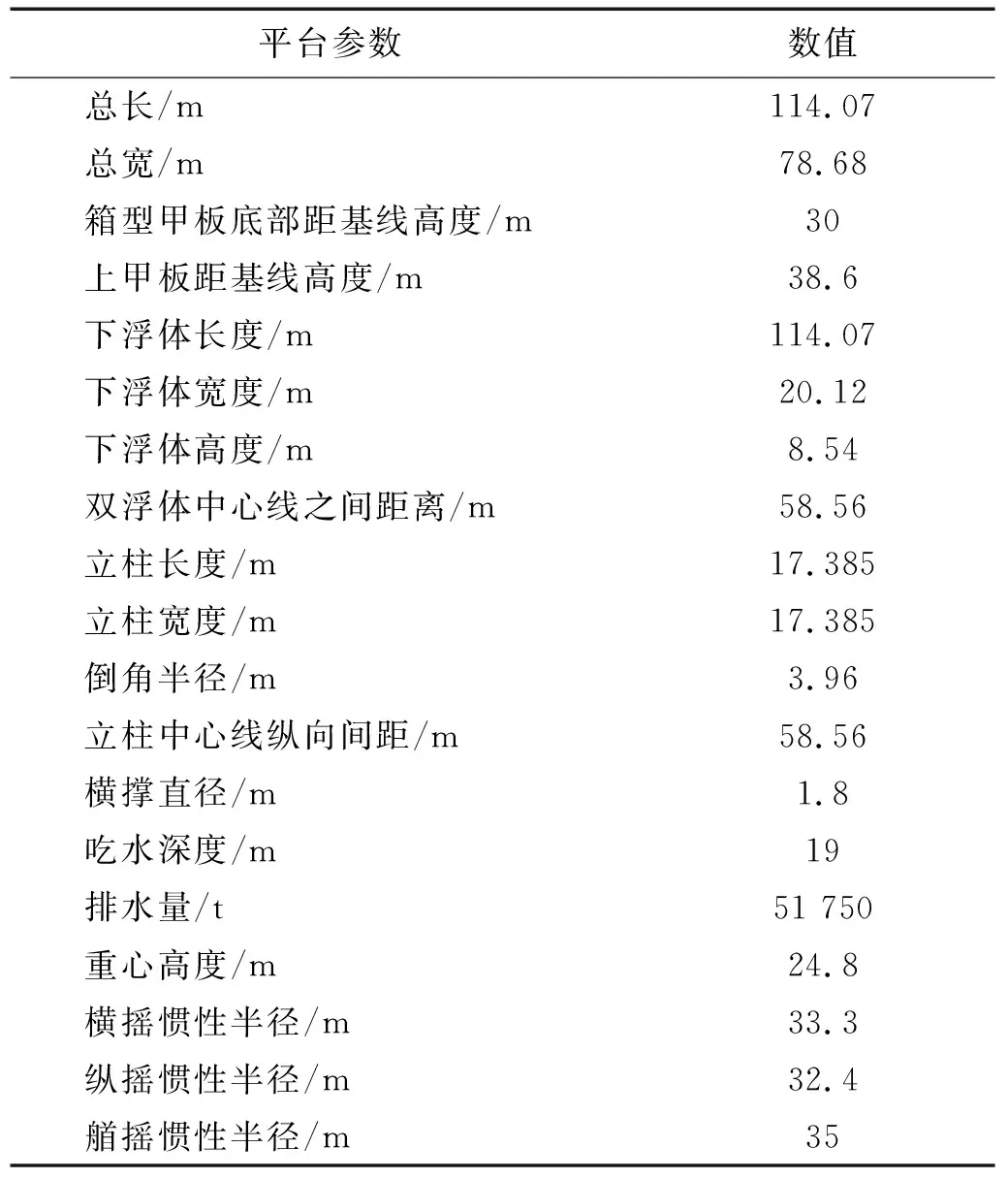
表1 半潜式平台模型参数Tab.1 Parameters of semi-submersible platform model

由于本文只关注半潜式平台在环境载荷作用下的运动性能,而不进行结构应力计算分析。所以,只需要建立半潜式平台湿表面模型即可。同时,由于在计算时忽略了水的黏性,所以在立柱和下附体内部建立莫里森杆件,以补偿其拖曳力。最终所建立半潜式平台湿表面模型如图2所示。

图2 半潜式平台湿表面模型Fig.2 Hydrodynamic model of semi-submersible platform

2.2 半潜式平台系泊系统模型的建立

该半潜式平台悬链式系泊系统总共有12根缆。每根缆总长3 950 m,水平跨距3 500 m,由甲板锚链、复合缆和海底锚链三部分组成,各部分分别长450 m,2 000 m和1 500 m。其材料属性如表2所示。

表2 系泊缆材料参数Tab.2 Material parameters of the mooring line

如图3所示,12根系泊缆被分为四组,对称分布在4根立柱外侧。导缆孔距基线高度为18.49 m,每组中间那根系泊缆的导缆孔位于立柱中心线上,左右2根系泊缆的导缆孔在水平线上分别距其3 m。每组的3根系泊缆与水平方向的夹角分别为37°,40°和45°。

图3 半潜式平台系泊缆平面布置图Fig.3 Layout of the mooring line

2.3 半潜式平台模型验证

本文所选取的半潜式平台模型与李长东等所研究的半潜式平台模型一致。为验证所建立模型的正确性,选取相关频域计算结果与已发表文献进行对比。结果如图4所示。

图4 频域计算结果对比图Fig.4 Comparison of frequency domain results

由图4可知,本文计算结果与相关文献取值基本一致。因此,所建模型准确无误,后续计算可以采用。

3 系泊失效前后半潜式平台运动性能

3.1 海洋环境条件

半潜式平台工作海域海况参数如表3所示。

表3 工作海域海况参数Tab.3 Sea state parameters of working area

在进行仿真模拟计算时,风设置为均匀风,流设置为均匀流,波浪采用工程界常常使用的波浪谱方式从能量分布的角度来模拟。

本文所采用的波浪谱为JONSWAP谱,本质为P-M谱的变形。其表达式为

(10)

系数α为无因次风区的函数,即

(11)

式中:U为海面以上10 m高度处的风速;x为风区长度。

谱峰频率为

(12)

σ为峰形系数,其值为

(13)

式中,γ为谱峰升高因子,定义如下

(14)

γ的观测值范围是1.5～6.0,平均值为3.3。本文取2,其是根据南海实际环境观测数值统计得出的。

3.2 系泊失效前后半潜式平台运动响应分析

在定义工作海域海况参数时,保持风浪流同向入射进行时域计算分析。入射角度分别为0°,15°,30°,45°,60°,75°和90°,以探究不同入射角度下系泊缆张力最大值。经时域计算分析得到系泊完整条件下各个系泊缆张力最大值示意图,如图5所示。

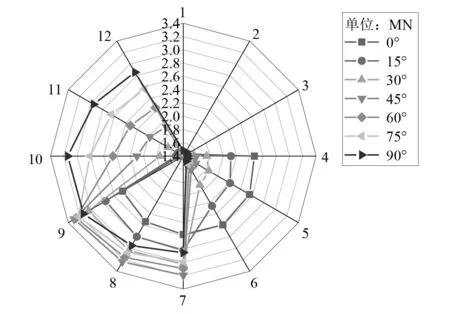
图5 系泊缆张力最大值示意图Fig.5 Maximum tension of cable

由图5可知,风浪流同向45°入射时,半潜式平台9号系泊缆张力最大值最大,约为3.298 MN。根据相关文献,半潜式平台系泊缆在作业工况下的安全系数(系泊缆破断强度与其最大张力的比值)为2.5[21]。因此,结合表2计算出,风浪流同向45°入射时,9号系泊缆的安全系数值小于2.5。考虑到疲劳、腐蚀和人为破坏等其他因素,此时出现系泊失效情况的概率相对较高。

后续保持风浪流同向45°入射,断开9号系泊缆以研究半潜式平台在系泊失效后的运动性能。又因为在系泊完整条件下,半潜式平台六个自由度方向上的运动响应在2 000 s时已经相对比较稳定,所以选择在中间时刻即2 000 s,去断开9号系泊缆。

保持风浪流同向45°入射,系泊完整条件下和9号系泊缆失效条件下,半潜式平台在六个自由度方向上的运动响应对比如图6所示。

图6 半潜式平台六自由度运动响应时程对比图Fig.6 Comparison of 6 DOFs motion response

由图6可知,风浪流同向45°入射时,相比于系泊完整条件,在9号缆失效条件下,半潜式平台在垂荡、横摇、纵摇和艏摇方向上的运动响应变化较小,在纵荡和横荡方向上的运动响应最大值分别增大52%和37%。而动力定位系统可以通过推进器产生的推力,很好地控制半潜式平台在平面内,即在纵荡、横荡和艏摇方向上的运动响应,有效地补偿系泊失效后带来的运动响应变化。因此,后续将研究使用无模型自适应控制作为动力定位系统控制理论,通过动力定位系统来弥补系泊失效后带来的运动响应变化。

在海洋环境条件的作用下,半潜式平台在海面上的运动可视作低频运动与波频运动的叠加。保持风浪流同向45°入射,9号缆失效2 000 s内,半潜式平台在纵荡、横荡和艏摇三自由度方向上的低频和波频运动响应如图7所示。

图7 半潜式平台三自由度方向上的低频和波频运动响应时程图Fig.7 Low frequency motion response and wave frequency motion response of 3 DOFs

由图7可知,波频运动主要引起平台在平衡位置附近周期往复运动,其是由一阶波浪力引起的,并不会使平台偏离初始位置。而低频运动主要引起平台大幅度偏移运动,其是由风力、流力和二阶波浪力共同作用引起的。因此,在后续使用动力定位系统时,只需保留由风力、流力、二阶波浪力和推进器推力共同作用引起的低频运动进行反馈,从而有效地减小波频运动带来的推进器磨损。

4 基于无模型自适应控制的半潜式平台系泊失效后运动性能恢复

4.1 三种动态线性化方法

MFAC通过引入伪偏导数、伪梯度、伪雅可比矩阵和伪阶数等新概念,将非线性系统等价转换为一系列基于输入输出增量形式的动态线性化数据模型。利用系统输入输出数据实时在线估计伪雅可比矩阵,实现系统的自适应控制。

在进行无模型自适应控制器设计之前,首先需要对非线性系统进行动态线性化。其主要有紧格式动态线性化(compact form dynamic linearization, CFDL)、偏格式动态线性化(partial form dynamic linearization, PFDL)和全格式动态线性化(full form dynamic linearization, FFDL)三种方法。在这其中,紧格式动态线性化仅考虑了系统在下一时刻的输出变化量与当前时刻的输入变化量之间的时变动态关系,偏格式动态线性化还考虑了系统在下一时刻的输出变化量与当前时刻的一个固定长度滑动时间窗口内的输入变化量之间的时变动态关系,而全格式动态线性化则将当前时刻具有某个长度的滑动时间窗口内的所有控制输入变化量和系统输出变化量对下一时刻系统输出变化量的影响都考虑进来。因此,当系统的输出伪阶数Ly=0时, 全格式动态线性化就转变为了偏格式动态线性化;当系统的输出伪阶数Ly=0和输入伪阶数Lu=1时, 全格式动态线性化就转变为了紧格式动态线性化。

半潜式平台动力定位控制系统可以根据当前时刻纵荡、横荡和艏摇方向上的低频运动响应,利用期望位置和艏向,来计算出需要施加到平台的控制作用力,属于多输入多输出离散时间非线性系统。其全格式动态线性化过程可描述如下:

考虑如下多输入多输出离散时间非线性系统

y(k+1)=

f[y(k),…,y(k-ny),u(k),…,u(k-nu)]

(15)

式中:y(k)∈m和u(k)∈m分别为当前时刻系统的位置输出和控制力输入;f(·)为未知的非线性函数;ny和nu分别为未知的系统输出阶数和输入阶数。

定义Hyu(k)=[yT(k),…,yT(k-Ly+1),uT(k),…,uT(k-Lu+1)]T∈m(Ly+Lu),Ly和Lu分别为系统的输出伪阶数和输入伪阶数。

对非线性系统式(15)作如下假设:

假设1非线性函数f(·)的各个分量关于Hyu(k)的各个分量都存在连续偏导数。

假设2非线性系统式(15)满足广义Lipschitz条件,即对于任意时刻k和ΔHyu(k)≠0,均有

‖Δy(k+1)‖≤b‖ΔHyu(k)‖

(16)

式中,b>0为一个常数。

若式(15)满足假设1和假设2,且对所有时刻k有‖ΔHyu(k)‖≠0,式(15)可以等价地表示为如下全格式动态线性化模型

y(k+1)=y(k)+Φyu(k)ΔHyu(k)

(17)

式中,Φyu(k)=[Φ1(k),Φ2(k),…,ΦLy+Lu(k)]为分块伪雅可比矩阵,且对于任意时刻k有界。

4.2 控制律导出

在对半潜式平台动力定位控制系统进行动态线性化之后,可对控制器实现伪雅可比矩阵在线估计,进而导出控制律。

假设ΦLy+1(k)是满足如下条件的对角占优矩阵, 且ΦLy+1(k)中所有元素的符号对任意时刻k保持不变。考虑如下控制性能指标函数

J[u(k)]=‖yr(k+1)-y(k+1)‖2+
λ‖u(k)-u(k-1)‖2

(18)

式中:yr(k+1)为期望位置和艏向;λ>0为权重因子。将式(17)代入性能指标函数式(18)中,对J[u(k)]关于u(k)求极值,进而得到Φyu(k)的估计方法为

(19)

(20)

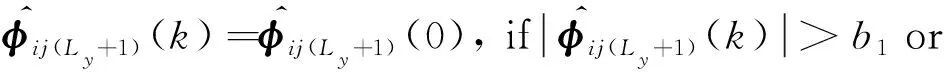
(21)

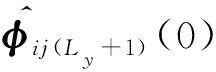
在对分块伪雅可比矩阵进行在线估计的同时,得到如下简化控制律

(22)

式中:ρi为步长因子;i=1,2,…,Ly+Lu;λ>0为权重因子。

4.3 控制算法设计

在进行动力定位控制系统设计时,只需保留低频运动进行反馈。利用分块伪雅可比矩阵的在线实时估计和控制律更新输入,即可建立动力定位系统无模型自适应控制算法。其流程如图8所示。

图8 无模型自适应控制流程图Fig.8 Flow of model-free adaptive control

步骤1设置控制器输入/输出初值和雅可比矩阵初值,以及参数η,μ,ρ和λ。

步骤2采集当前时刻半潜式平台纵荡、横荡和艏摇方向上的低频运动响应,以及半潜式平台期望位置。

步骤3根据相应公式在线实时估计伪雅可比矩阵。

步骤4根据相应控制律计算并对半潜式平台施加控制作用力。

步骤5k=k+1,返回步骤2,继续循环。

4.4 数值仿真模拟

在利用AQWA软件进行数值仿真模拟时,由于9号缆失效后半潜式平台艏摇方向上运动响应变化不大,所以半潜式平台艏摇方向上的期望位置设置为零即可。相比于基于紧格式动态线性化的无模型自适应控制,基于偏格式动态线性化的无模型自适应控制还考虑了当前时刻的系统输出变化量与前一时刻控制输入变化量之间的关系,即输入伪阶数为2。而相比于基于偏格式动态线性化的无模型自适应控制,基于全格式动态线性化的无模型自适应控制还考虑了当前时刻系统输出变化量与前一时刻系统输出变化量之间的关系,即输出伪阶数为1、输入伪阶数为2。

在进行控制器参数调节时,步长因子ρ在控制系统中起着绝对性的作用[22]。保持三种控制器中相关参数一致,采用试凑法来调节各个方向上的步长因子。以响应恢复速度和达到稳定后的状态为基准,通过调节发现,在一定变化范围内,控制器均能达到很好的控制效果。施加动力定位系统后,半潜式平台在纵荡、横荡和艏摇方向上的运动响应对比如图9所示。

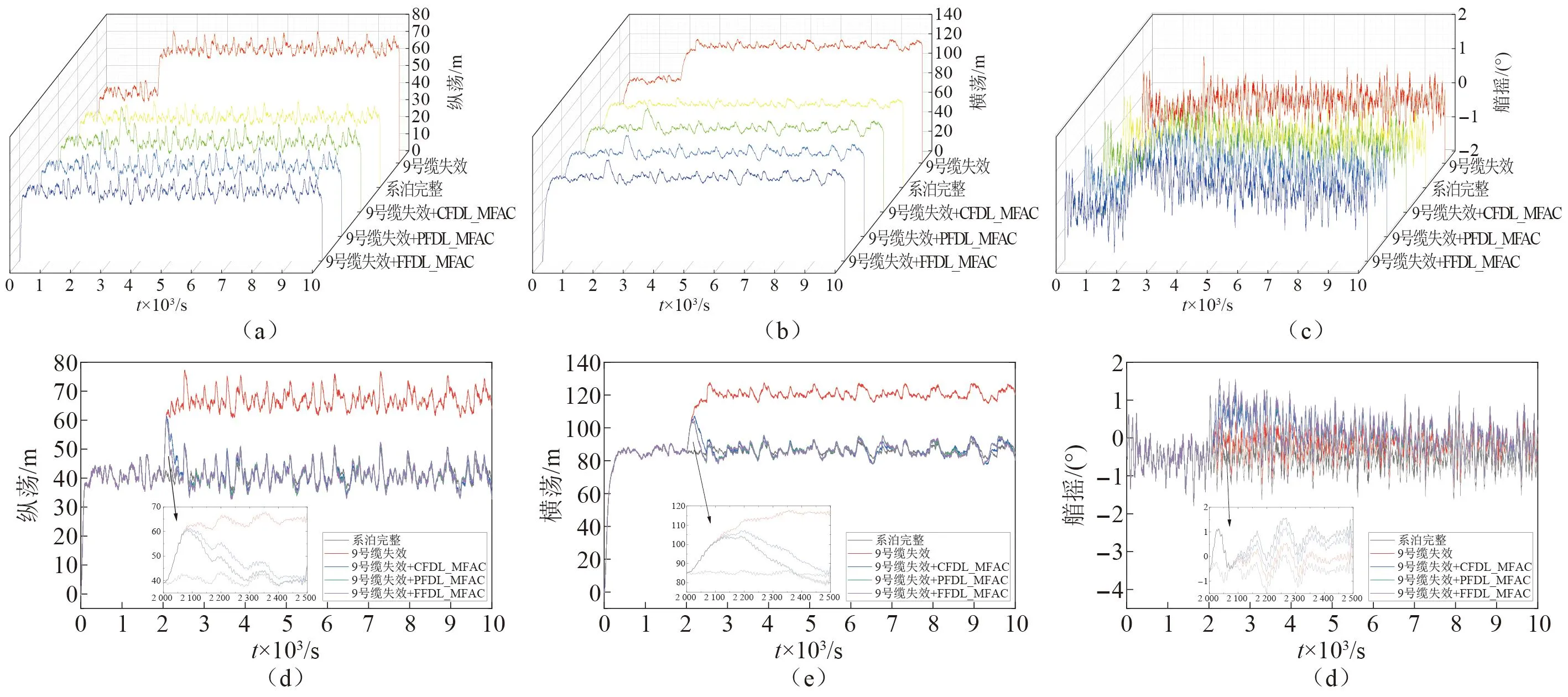
图9 半潜式平台纵荡、横荡和艏摇运动响应时程对比图Fig.9 Comparison of the surge, sway and yaw motion response

由图9可知,基于紧格式动态线性化的无模型自适应控制能让半潜式平台在系泊失效后500 s,恢复到与系泊完整条件下基本一致的运动响应。而基于偏格式动态线性化和全格式动态线性化的无模型自适应控制则能让半潜式平台在系泊失效后380 s,恢复到与系泊完整条件下基本一致的运动响应。由于系泊失效后半潜式平台在艏摇方向上运动响应变化并不是很明显,且艏摇方向上的期望位置为零。所以,其在一段时间内逐步恢复到零上下即可满足控制需求。因此,相比于基于紧格式动态线性化的无模型自适应控制,基于偏格式动态线性化和全格式动态线性化的无模型自适应控制能让半潜式平台响应恢复速度更快。同时,在控制效果方面,两者之间的差别不大。

此外,半潜式平台系泊失效后,施加采用以上三种控制方式的动力定位系统,在其达到稳定状态后,纵荡和横荡方向上的运动响应和系泊完整条件下基本一致,艏摇方向上的运动响应则维持在零上下。

无论是系泊失效条件下,还是失效后施加动力定位系统,与9号系泊缆一组的2根系泊缆,即7号和8号系泊缆的张力变化较大。其张力时程对比如图10所示。

图10 7号和8号系泊缆张力时程对比图Fig.10 Comparison of tension of No.7 and No.8 mooring line

由图10可知,系泊失效条件下,7号系泊缆和8号系泊缆张力最大值分别增大33%和34%。而系泊失效后施加动力定位系统,7号系泊缆和8号系泊缆张力最大值以及达到稳定状态后的张力值均显著减小。因此,在系泊失效后施加动力定位系统,不仅可以很好地补偿系泊失效带来的运动响应变化,而且可以有效减小系泊失效带来的相应系泊缆张力变化,进而减轻系泊失效带来的危害。

5 结 论

本文以一艘工作在我国南海海域、装配有悬链式系泊系统以及DP-3动力定位系统的半潜式平台为研究对象,利用AQWA软件进行计算分析,得到的最终结论如下:

(1) 由于半潜式平台自身运动特性,系泊失效前后,半潜式平台在纵荡和横荡方向上的运动响应最大值分别增大52%和37%,在垂荡、横摇、纵摇和艏摇四个自由度方向上的运动响应变化不大。

(2) 系泊失效后,采用无模型自适应控制作为动力定位系统控制理论的半潜式平台可以很好地控制自身在纵荡和横荡方向上的运动响应,减小系泊失效带来的危害。同时,由于推进器产生平面内推力的关系,艏摇方向上的运动响应也能得到很好地控制。

(3) 在系泊失效后半潜式平台运动响应控制效果方面,基于偏格式动态线性化和全格式动态线性化的无模型自适应控制比基于紧格式动态线性化的无模型自适应控制能让半潜式平台具有更快的响应恢复速度。但在控制效果方面,两者之间的差别不大。