耐张型悬索支撑输电结构风振非线性有限元分析

李正良, 王邦杰, 王 涛

(1. 重庆大学 土木工程学院,重庆 400045; 2. 重庆大学 风工程及风资源利用重庆市重点实验室,重庆 400045; 3. 哈尔滨工业大学 交通科学与工程学院,哈尔滨 150040; 4. 哈尔滨工业大学 重庆研究院,重庆 401151)

作为电力能源基础设施,高压输电塔-线体系[1]是电网中输配电系统的重要组成部分。随着电网建设的蓬勃发展,架设在山区地形中的输电结构不断增多[2]。然而,山区输电线路走廊所需路径愈发紧张,塔位选择亦愈发困难。如输电塔-线体系在广西喀斯特地貌、新疆丹霞地貌等特殊、复杂山区地形走线时,塔位受地形地貌限制经常难以成立,以至于造成线路大范围改线。

为此,电力行业在近年来开始探索适用于山区的新型输电结构,耐张型悬索支撑输电结构是其中一种新型架空输电结构。该输电结构主要由导线、地线、支撑导线悬索、支撑地线悬索、耐张绝缘子串和固定支架等组成,其工程效果图和结构示意图如图1所示。其中,由高强度钢绞线制成的悬索为主要承重结构,其通常固定在山体岩石中或刚性固定支架上;输电线通过连接金具与悬索形成耦联系统。

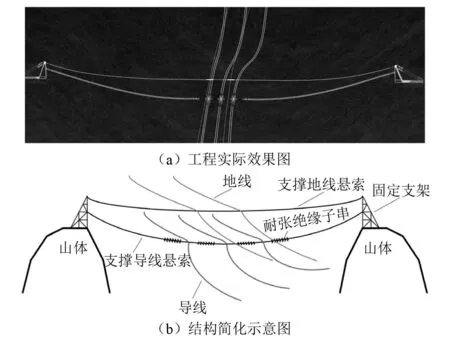
图1 耐张型悬索支撑输电结构示意图Fig.1 Schematic diagram of the tension suspension-braced transmission structure

耐张型悬索支撑输电结构中支撑悬索和输电线均为大跨度、高柔空间悬索结构,其为典型的风敏感结构;另外,该结构具有变形大、应变小等力学特点,几何非线性效应显著。耐张型悬索支撑输电结构与传统输电塔-线体系相比,既有相似特征,也有明显的不同之处。相似之处在于该结构和输电塔-线体系均具有高柔特征,均为风敏感结构。而不同之处在于该结构的输电线与支撑悬索形成耦联系统,其几何非线性效应更加显著。

针对输电线[3-4]和输电塔-线体系的风致非线性振动问题,学者们已开展了一系列的研究。冯珂等[5]建立了基于整体坐标系下三节点索单元的输电导线非线性动力学分析模型,并采用Newmark-β法进行了下击暴流作用下输电导线风致响应分析,结果表明在下击暴流风荷载作用下输电导线的动力响应非常显著;左太辉[6]采用ANSYS软件中的Link8单元建立了导线-绝缘子串耦合体系有限元模型,针对两跨导线结构体系在风荷载作用下的非线性响应开展了研究,建议增大导线设计风荷载;邓洪洲等[7]通过非线性有限元分析方法建立了跨越输电塔-线体系动力学模型,并选用Newmark-β法进行相应的时程分析,指出大跨越输电塔-线体系风致非线性振动分析应考虑塔线耦合影响。整体而言,就输电线和输电塔-线体系的动力学分析模型及其风致非线性振动问题,学者们通过理论研究和数值模拟进行了较为细致的分析,亦取得了较为显著的研究成果。然而,耐张型悬索支撑输电结构的非线性动力学模型及风致振动分析鲜有文献报道。

为此,本文基于三维杆单元建立了耐张型悬索支撑输电结构有限元模型;然后形成了该结构非线性动力方程,并给出了结合Newton-Raphson法的Newmark-β法迭代求解过程;而后以两跨耐张型悬索支撑输电结构为例,进行了模态分析、位移时程分析,并分析了风速和风向角对结构响应的影响。

1 耐张型悬索支撑输电结构简化力学模型

1.1 结构参数及边界条件

耐张型悬索支撑输电结构简化模型和结构参数,如图2所示。ls为同一悬索两侧固定点的水平距离;lc为相邻两跨悬索的水平距离;hs为同一悬索两侧固定端的高差;hc为同一跨导线或者地线在相邻悬索挂点位置之间的高差;hwg为支撑地线悬索端点与对应的支撑导线悬索端点之间的高差。

图2 耐张型悬索支撑输电结构简化模型及结构参数Fig.2 Simplified model and structural parameters of the tension suspension-braced transmission structure

支撑悬索的端部与固定支架的连接点和输电线与相应悬索在边界处的连接点,连接方式均为铰接。因此,耐张型悬索支撑输电结构边界处均可考虑为固定铰支座。

1.2 结构初始形状

为了建立考虑几何非线性效应的耐张型悬索支撑输电结构有限元模型,需要先获得其在重力荷载作用下的初始位形和初始内力。对于耐张型悬索支撑输电结构的支撑悬索和输电线,其初始形状可简化为抛物线模型,建立该抛物线模型所需的函数表达式为

y=4xfm(1-x/l)/l

(1)

式中:y为计算点到起点的垂直距离;x为计算点到起点的水平距离;l为终点到起点的水平距离;fm为跨中弧垂,按式(2)计算

(2)

式中:q为支撑悬索或输电线单位体积内的重力荷载;σ0为悬索水平应力;β为高差角,tanβ=h/l,其中h为hs或hc,l为相应的ls或lc。

1.3 结构受力特性

在耐张型悬索支撑输电结构中,支撑悬索和输电线主要承受张力作用,其次还会承受弯矩和扭矩作用。在不考虑扭转的风振响应分析中,忽略其抗弯能力和抗扭能力是合理的[8]。因此,在耐张型悬索支撑输电结构风致振动分析中,支撑悬索和输电线主要考虑轴向抗拉能力。

2 耐张型悬索支撑输电结构风振非线性有限元分析模型

2.1 支撑悬索和输电线单元刚度矩阵

根据耐张型悬索支撑输电结构的力学特点,其支撑悬索和输电线风振属于大变形小应变问题。结合该输电结构受力特性,可采用考虑几何非线性效应的三维杆单元建立如图3所示的有限元模型。一般而言,单元刚度矩阵可通过局部坐标系和整体坐标系两种方式进行建立。相较于局部坐标系下建立的刚度矩阵[9-10],整体坐标系下的单元刚度矩阵[11-15]可直接组集为体系刚度矩阵且有效避免坐标转换处理,提高计算精度。对于整体坐标系下的三维杆单元,其刚度矩阵的推导方式大多为虚功原理和对杆端力求导。然而虚功原理需要进行多重积分,且其结果往往为隐式刚度矩阵,难以直接应用;杆端力求导则需要进行较为繁杂的向量运算。为此,本文通过三维杆单元应变能和其变形之间的关系简化运算,在整体坐标系下推导三维杆单元显式刚度矩阵。

图3 简化有限元模型及节点位移Fig.3 Simplified finite element model and node displacements

在图3中,初始时刻(即C0状态)的物理量为已知量,此时,整体坐标系下的单元两端节点向量为

0ai={xiyizi}T,
0aj={xjyjzj}T

(3)

再利用矢量相减原理可得到整体坐标系下杆单元的单元向量

0ae=0aj-0ai={xj-xiyj-yizj-zi}T

(4)

经过t时间后,杆单元发生位移变形运动至C1状态,在该时刻下,整体坐标系下的单元两端节点位移向量为

ui={uiviwi}T,
uj={ujvjwj}T

(5)

由式(3)和式(5)可得整体坐标系下的单元两端节点向量分别为

tai=0ai+ui,
taj=0aj+uj

(6)

因此,t时刻下杆单元的单元向量为

tae=0ae+uj-ui

(7)

根据节点位移向量,单元位移向量可表示为

ue={uiviwiujvjwj}T

(8)

利用式(8)可将式(7)进一步表示为

tae=0ae+[-I3×3I3×3]ue

(9)

式中,I3×3为3阶单位矩阵。

C0状态下杆单元无应变,其单元长度为

(10)

C1状态下杆单元长度为

(11)

此时,杆单元的应变为

(12)

t时刻杆单元应变能tU可按式(13)计算

(13)

式中:σ(ε)为杆单元的应力,在线弹性范围内,应力与应变的关系为σ(ε)=Eε,E为单元弹性模量;V为单元体积;当杆单元横截面积为定值A时,式(13)可进一步表示为

(14)

整体坐标系下,t时刻单元切线刚度矩阵可利用海森矩阵计算得到

(15)

t时刻单元切线刚度矩阵最终结果为

(16)

因式(16)所示的单元切线刚度矩阵tKe在推导过程中仅引入了线弹性假定,而没有引入小变形假定,其为任意位移下的精确切线刚度矩阵,故而其适用于任意大变形小应变的情况。

2.2 单元质量矩阵和阻尼矩阵

耐张型悬索支撑输电结构有限元模型质量矩阵采用一致质量矩阵构建,其单元一致质量矩阵[16]为

(17)

式中:0l为单元初始长度;ρ为单元的质量密度。

利用Rayleigh阻尼构建单元阻尼矩阵

tCe=αvMe+βvtKe

(18)

式中,αv和βv为Rayleigh阻尼常数,分别按式(19)和式(20)计算

αv=2ξk1ωk1ωk2/(ωk1+ωk2)

(19)

(20)

式中:ωk1和ωk2分别为k1阶和k2阶模态的固有频率;ξk1和ξk2分别为对应于k1阶和k2阶模态的阻尼比。悬索结构具有强几何非线性,刚度矩阵tKe会不断变化,可取βv=0,位移结果是偏安全的,此时,tCe不受结构位移变化的影响,即为Ce。

2.3 等效节点荷载向量

耐张型悬索支撑输电结构所承受的主要荷载为重力荷载和风荷载。该输电结构的静力和动力位移以重力荷载平衡位置为基准,因此,在计算结构等效节点荷载向量时,重力荷载等效为基准位置的内部节点荷载向量。对于耐张型悬索支撑输电结构有限元模型的杆单元,其单位长度上的风荷载按式(21)计算

(21)

式中:ρair为空气密度;Vz为风速;CD为阻力系数;Am为杆单元单位长度上顺风向投影面积,对于支撑悬索:Am=dcosθ,对于输电线:Am=dsinθ,d为杆单元直径,θ为风向角,如图4所示。

图4 风向角θ示意图Fig.4 Schematic diagram of wind direction angle θ

Vz按式(22)计算

Vz=Vs(z)+V(t)

(22)

式中:Vs(z)为平均风速;V(t)为脉动风速。

脉动风速V(t)可采用谐波合成法[17]获得。平均风速Vs(z)可根据指数律按式(23)计算

(23)

式中:V10为10 m高度处的参考平均风速;z为高度;α为地面粗糙度系数,由于耐张型悬索支撑输电结构处于山地地形,其地面粗糙度类别可考虑为C类,根据GB 50009—2012《建筑结构荷载规范》[18],α取为0.22。

将单元上的风荷载转换为单元等效节点荷载,即

(24)

式中,Fix为风荷载在i节点上X方向的等效节点荷载,其余以此类推。

2.4 非线性动力方程的建立

将耐张型悬索支撑输电结构的各个单元的质量矩阵、刚度矩阵、阻尼矩阵和等效节点荷载向量分别进行组集,基于更新的Lagrange列式,在基准位置处建立结构非线性动力方程

(25)

当Δt足够小时,结构在一个时间步内的位移增量很小,t+ΔtQ和tK可近似为如下线性关系

t+ΔtQ=tQ+tKu

(26)

式中:tQ为t时刻的内部节点荷载向量;tK为结构在t时刻的刚度矩阵;u为结构在Δt内的位移增量, 即u=t+Δtu-tu。

结合式(25)和式(26),可得位移增量形式的非线性动力方程

(27)

2.5 非线性动力方程的求解

本文采用Newmark-β法求解式(27)所示的非线性有限元方程。由于式(26)为线性近似结果,随着时间步的增加,求解的位移增量会产生较大的误差累积。因此,为了提高解的精度和避免数值不稳定性的累积,在每个时间步内,本文采用Newton-Raphson迭代法进行平衡迭代计算。求解过程归纳如下:

步骤1根据单元初始位形和应变计算各个单元特性矩阵0Ke,Me和Ce,再进行组集得到结构的特性矩阵0K,M和C。

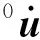
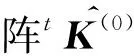
式中:tQ(0)为第一次迭代前的内部节点荷载向量;t+Δtu(0)为第一次迭代前的位移,即tu。

求解t+Δt时刻第一次迭代后的位移增量u(1)

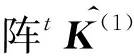
t+Δtu(1)=t+Δtu(0)+u(1)

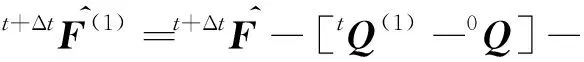
并计算第二次迭代后的位移增量u(2)

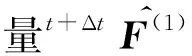
3 算例分析

本文以如图5所示的两跨耐张型悬索支撑输电结构为研究对象,进行模态分析和位移时程分析,并研究风速V10和风向角θ对结构风振响应的影响。两跨耐张型悬索支撑输电结构的结构参数分别为:ls=1 000 m,lc=800 m,hwg=20 m,hs=0和hc=0,支撑导线悬索的端点考虑为固定在300 m高处。本文分析所需的计算均在Intel i5-9400F CPU、32 GB RAM的计算机上进行。

图5 两跨耐张型悬索支撑输电结构Fig.5 The two-span tension suspension-braced transmission structure

3.1 模态分析

通过本文模型,可计算该输电结构的前五阶固有频率和前三阶振型分别如表1和图6所示。通过表1频率分析结果可知,悬索支撑导线部分的前五阶固有频率分别为悬索支撑地线部分相应值的77.89%,78.65%,78.28%,78.30%和78.30%。悬索支撑导线部分的低阶固有频率比悬索支撑地线部分的低阶固有频率小。由图6可得,第一阶振型为反对称竖弯,第二阶振型为对称侧弯,第三阶振型为反对称侧弯。

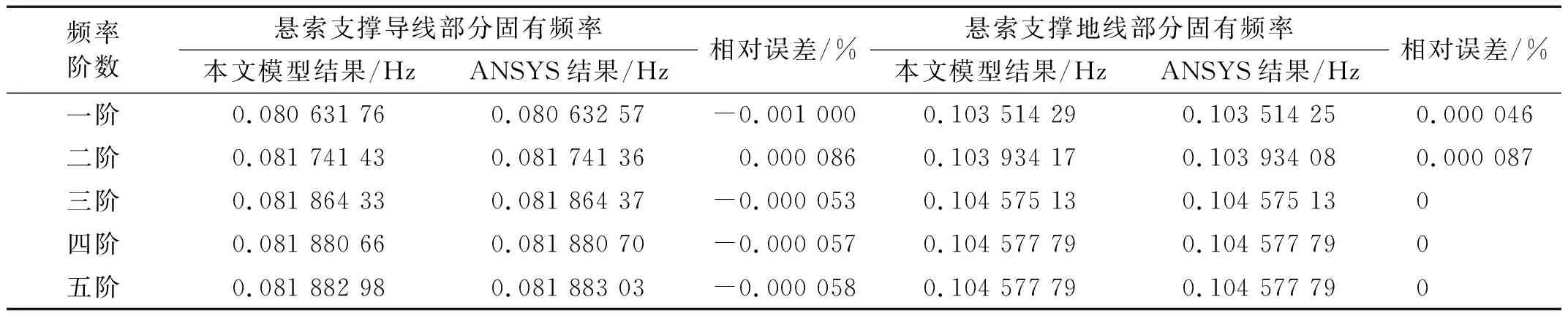
表1 结构前五阶固有频率Tab.1 First five orders natural frequency of the structure

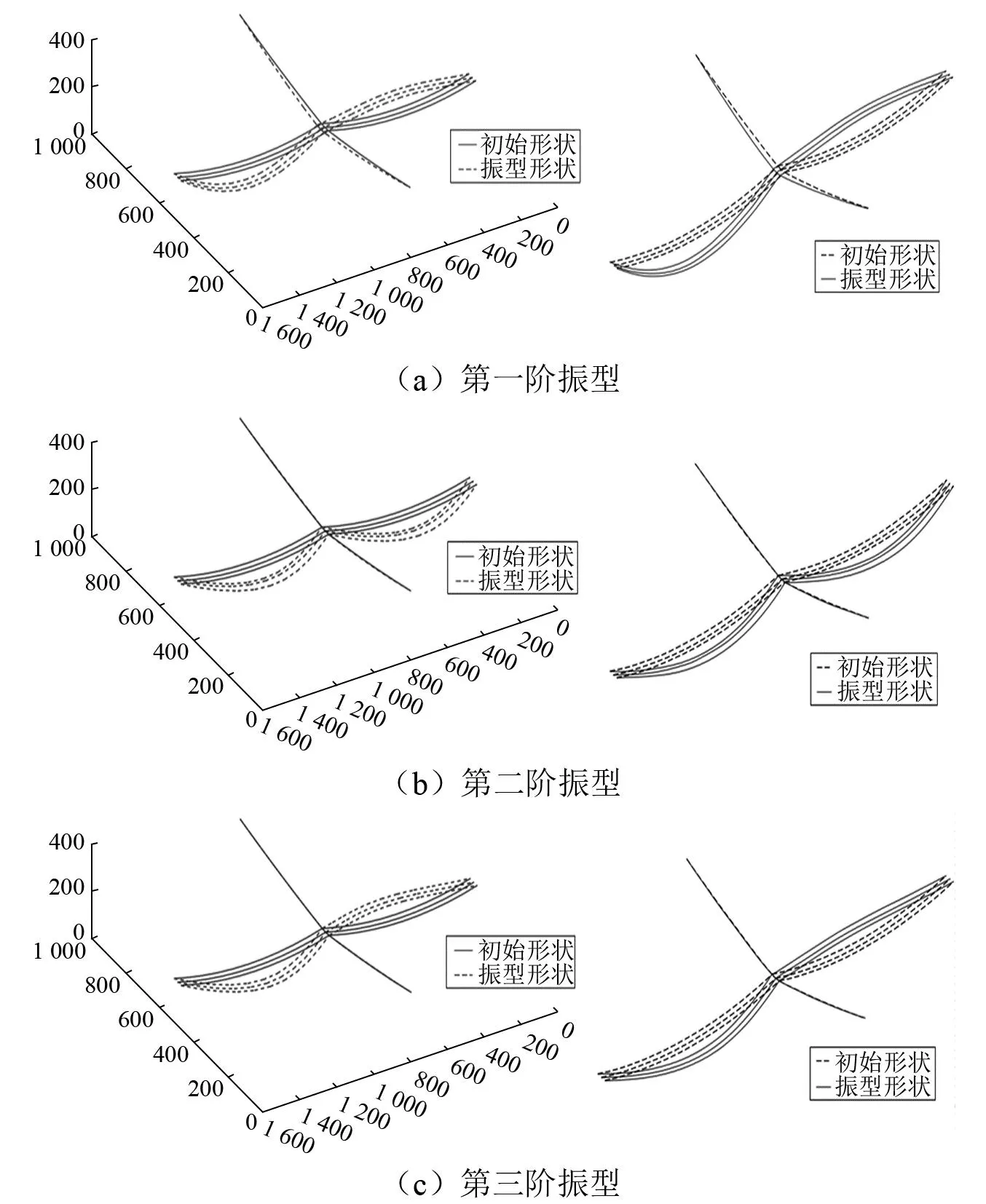
图6 本文模型(左)和ANSYS(右)求得的悬索支撑导线部分前三阶振型Fig.6 First three orders mode of vibration of the suspension-braced conductor part obtained by the proposed model (left) and ANSYS (right)

为了验证本文模型的正确性和计算精度,另外采用ANSYS进行模态分析,将两者计算结果进行对比。在ANSYS模型中,支撑悬索和输电线均采用Link180单元模拟,结构参数、边界条件及其他参数均与本文模型一致。表1和图6也分别给出ANSYS计算结果,可以发现,本文模型频率结果相对误差绝对值的最大值为0.001%,其精度较好,而振型结果亦基本准确。

3.2 位移时程分析

以风速V10=20 m/s和风向角θ=90°的工况为例,开展两跨耐张型悬索支撑输电结构的位移时程分析。通过本文模型可求得导线中点侧向位移时程曲线和200 s时刻的结构变形分别如图7和图8所示,图7中的侧向位移时程结果平均值和最大值如表2所示。表2和图7结果表明,输电导线中点在该工况风荷载作用下产生的侧向位移平均值为33.92 m,其最大值为48.49 m;该侧向位移从最小值0到最大值48.49 m均有分布,变化幅度较大。由图8可知,输电线不仅侧向位移较大,其竖向位移也较大。因此,可认为该输电结构的输电线位移响应受风荷载影响较显著。

表2 本文模型和ANSYS得到的平均值和最大值Tab.2 Average and maximum values obtained by the proposed model and ANSYS

图7 导线中点侧向位移时程Fig.7 The lateral displacement time history of the conductor midpoint

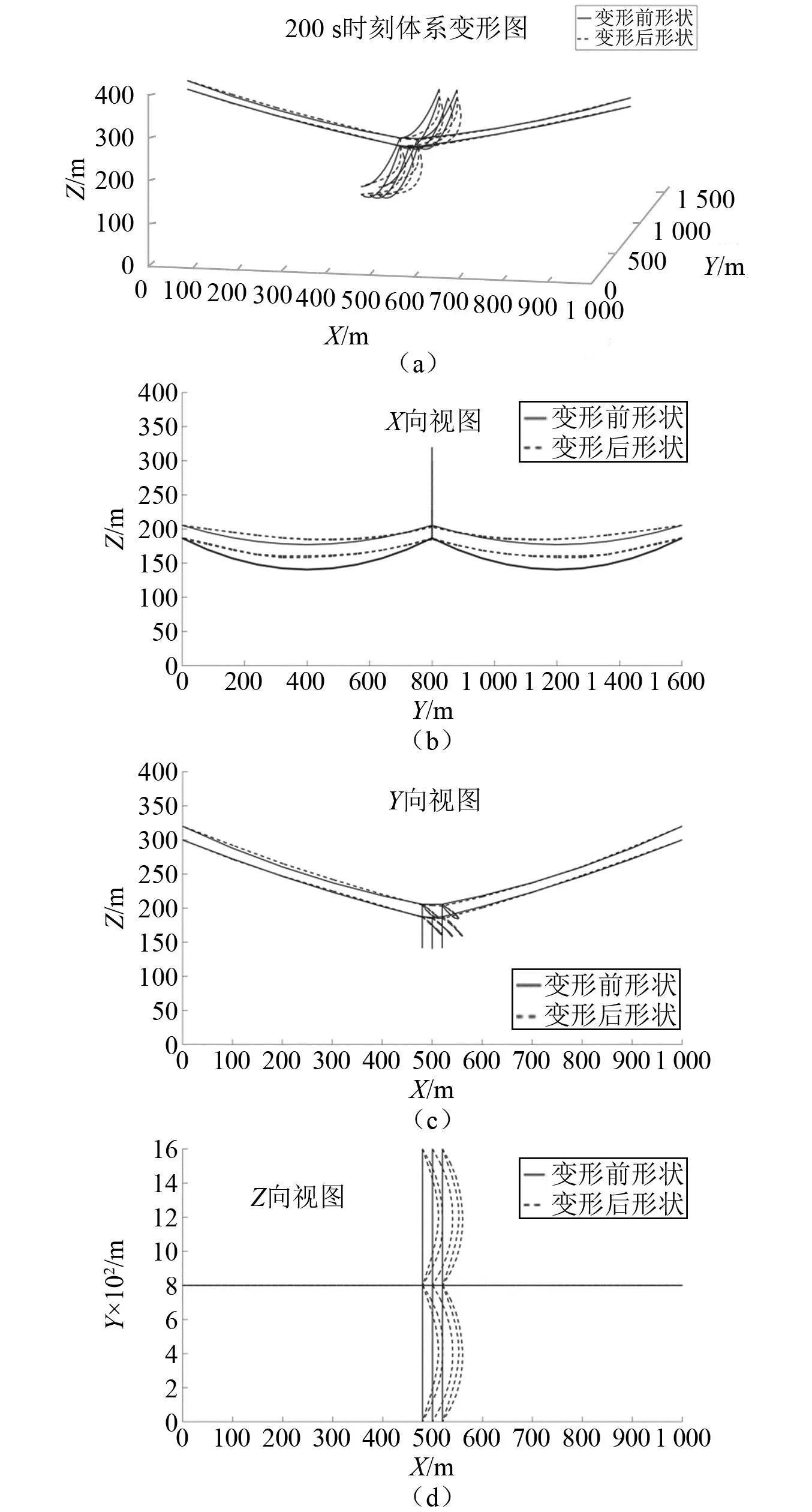
图8 200 s时刻的结构变形图Fig.8 Structural deformation at 200 s

类似的,ANSYS计算结果亦被绘制在图7和表2中,表3则给出了本文模型的计算效率。由图7和表2可知,本文模型求得的侧向位移时程结果平均值和最大值的相对误差分别为-0.09%和-0.53%,其精度较高。同时,本文模型求得的侧向位移时程曲线与ANSYS结果具有一致的趋势,其吻合度较高。表3结果表明,ANSYS进行导线中点侧向位移时程分析所需的计算时间为28.12 min,而本文模型计算时间为1.85 min,其计算成本仅为前者的6.58%。因此,本文模型能较为高效地应用于耐张型悬索支撑输电结构风振非线性有限元分析。

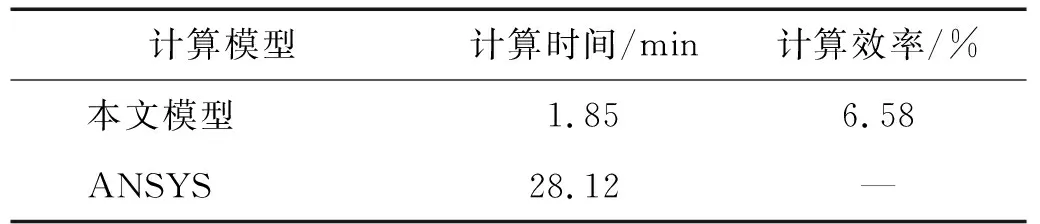
表3 本文模型和ANSYS计算效率Tab.3 Calculation efficiency obtained by the proposed model and ANSYS

3.3 风速影响分析

在θ=90°时,输电线最大侧向位移和支撑悬索最大张力随风速V10的变化情况,如图9所示。图9(a)中可以看出输电线最大侧向位移随着V10增大而增大,增大幅度呈现先快后慢的趋势,这一现象在导线上更加明显。在图9(b)中,支撑悬索最大张力随着V10的增大而一直增大。输电线最大侧向位移增大幅度的变化是由于结构的应力刚化效应,根据式(16),单元切线刚度会随着位移的增加而增大,结构的侧向刚度也会随着位移的增加而逐渐增大,当侧向刚度较大时,输电线侧向位移增大幅度会减缓。

图9 风速的影响Fig.9 The influence of wind speed

输电线最大侧向位移以导线最大侧向位移为例,风速为5 m/s,10 m/s,15 m/s,20 m/s,25 m/s和30 m/s,导线最大侧向位移分别为2.83 m,11.03 m,22.48 m,32.96 m,40.16 m和44.78 m,风速从5 m/s开始,每提高5 m/s,导线最大侧向位移分别增加8.20 m,11.45 m,10.48 m,7.21 m和4.62 m。因此,在风速较小时,风速的增大,会较显著地增加输电线最大侧向位移,而在风速较大时,输电线最大侧向位移受风速影响较小。支撑悬索最大张力的变化是由于悬索张力需要平衡等效节点荷载,风速增大,悬索张力也会一直增大。

支撑悬索最大张力以支撑导线悬索最大张力为例,风速从5 m/s开始,每提高5 m/s,支撑导线悬索最大张力分别增加6.59 kN,11.05 kN,15.62 kN,20.38 kN和25.47 kN,最大张力增量与风速近似成线性相关,最大张力与风速的二次方近似成线性相关;在风速较小时,支撑悬索最大张力受风速影响较小,而在风速较大时,支撑悬索最大张力受风速影响较显著。

因此,在风速较小时,输电线侧向位移受风速影响较支撑悬索张力更大,在风速较大时,支撑悬索张力受风速影响较输电线侧向位移更值得注意。

3.4 风向角影响分析

在V10=20 m/s时,输电线最大侧向位移和支撑悬索最大张力随风向角θ的变化情况如图10所示。图10(a)中可以看出输电线最大侧向位移随着θ增大而增大,增大幅度呈现先快后慢的趋势,在图10(b)中,支撑悬索最大张力随着θ的增大而增大。输电线最大侧向位移增大幅度的变化同样是由于结构的应力刚化效应。以导线为例,风向角为0°,45°,60°和90°,导线最大侧向位移分别为0.007 1 m,21.15 m,28.12 m和32.96 m,输电线最大侧向位移的最不利风向角为90°。支撑悬索最大张力随着风向角增大而增大的原因是输电线的顺风向投影面积比支撑悬索的顺风向投影面积大,随着风向角增大,结构所受的整体风荷载也增大。因此,风向角对输电线侧向位移和支撑悬索张力影响都较显著,两跨耐张型悬索支撑输电结构最不利风向角为90°。

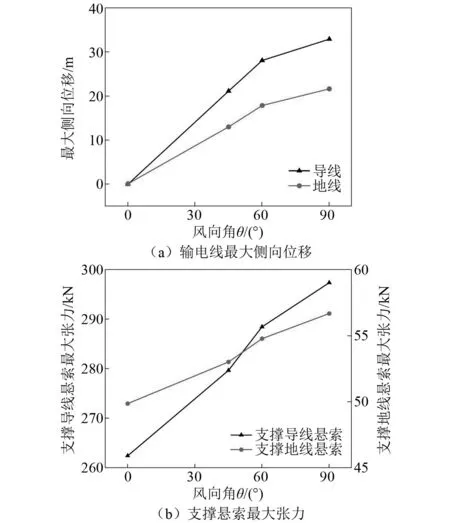
图10 风向角θ的影响Fig.10 The influence of wind direction angle θ

4 结 论

耐张型悬索支撑输电结构是一类适用于山地地形的新型输电结构。本文采用非线性有限元方法建立了耐张型悬索支撑输电结构风振非线性有限元分析模型,针对两跨耐张型悬索支撑输电结构,进行模态分析和位移时程分析,并讨论了风速和风向角对结构响应的影响。可得出主要结论如下:

(1) 对比结果显示本文模型所计算的固有频率和位移时程结果精度较高,能够准确计算结构动力特性和动力响应。本文模型亦具有较高的计算效率,其获得动力响应的计算成本仅为ANSYS的6.58%。

(2) 悬索支撑导线部分的低阶固有频率比悬索支撑地线部分的低阶固有频率更低,但两者数值仍处于同一数量级。悬索支撑导线部分前三阶振型分别为反对称竖弯、对称侧弯和反对称侧弯。

(3) 在风荷载作用下,输电导线中点侧向位移和竖向位移均较大,且其侧向位移变化幅度较大。因此,风荷载对该输电结构的输电线位移响应影响较为显著。

(4) 对于平均风荷载作用,在较小风速下,输电线侧向位移受风速影响较支撑悬索张力更大;在较大风速下,支撑悬索张力受风速影响较输电线侧向位移更值得注意。输电线侧向位移和支撑悬索张力受风向角影响均较显著,结构最不利风向角为90°。