基于两种梁理论对变幅锥形杆弯曲振动的特性分析及参数设计
常婷婷, 沈 峰, 鲍四元
(苏州科技大学 工程力学系,江苏 苏州 215011)
杆、梁结构的振动是工程中的基本问题。在超声领域,功率超声设备中的关键部件是超声变幅杆,其截面分为两种形式:阶梯形截面和连续变截面。其中圆锥形变幅杆[1]采用了连续变截面,在对放大系数不要求特别大的情况下具有非常广泛的应用。而连续变截面杆较普遍地用于具有较高的工作稳定性和较大的抗弯刚度要求的场合。纯弯曲振动模式的超声装置中超声加工中效率高且质量好而显得至关重要[2],部分超声加工中采用了兼有弯曲、纵向和扭转复合的振动模式,如万志坚等[3]从理论和试验上分别研究了一种面内弯纵复合模态的直线超声电动机。
目前,研究人员采用不同的方法对等截面梁做了大量的研究。采用的理论主要有欧拉梁理论和铁木辛柯梁理论。其中欧拉梁理论方面涌现了一些解析方法,如刘向尧等[4]基于简化的欧拉梁对有一定工程实践意义的三个模型进行了推导,得到三个对应频率方程的解析结果。牛国华等[5]则用直接解析解和矩阵传递法研究了组合变截面L型变截面梁的自由振动特性。Ma[6]利用一种精确梁单元分析刚架结构的自由振动并进行了优化分析。涌现的一些数值方法如Wang等[7]基于微分求积法分析了梁和刚架结构的动力学特性。吴林潮等[8]基于近场动力学方法研究了欧拉梁结构的振动特性。
而应用铁木辛柯梁理论方面,Han等[9]获得了等截面铁木辛柯梁的模态解析表达式,进而得到均匀圆截面简支铁木辛柯梁在移动荷载作用下动力学特性的解析解。Hamioud等[10]基于谱元法研究了铁木辛柯梁的振动问题,计算得到其固有频率和振型;李晓姣[11]基于应用力学的辛对偶体系方法,提出梁动力学问题的辛本征值分析方法,得到了铁木辛柯梁自由振动时的固有频率。Mohammad等[12]建立铁木辛柯梁单元,利用有限元法推导出该单元的质量矩阵、刚度矩阵和几何矩阵,求解出梁在不同边界条件下自由振动的固有频率。
研究表明,经典欧拉梁理论忽略了梁的横向剪切变形,但对于高度相对跨度不是很小的情况,如短而较高的梁,剪切变形的影响不能忽略,故铁木辛柯梁理论在梁运动方程中引入剪切变形和转动惯量。对于梁有效长度较短的情况,铁木辛柯梁理论计算梁的固有频率较欧拉-贝努利梁理论更符合实际。在研究超声变幅杆时,可采用铁木辛柯梁理论研究超声变幅杆的动力学特性[13]。
随着实际工程中变截面杆的大量应用,学者们对相关的动力学问题做了若干研究。葛仁余等[14]研究了轴向力作用下轴向功能梯度变截面梁的横向自由振动问题,但其理论主要基于欧拉-贝努利梁理论分析。对于变截面梁振动问题,由于弯曲振动方程的解析解数学处理上具有一定的难度,目前很多学者[15-16]应用各种近似解法进行了求解,即使采用解析方法,其求解形式和过程较为复杂。以上研究在分析变截面梁自由振动问题时较少采用基于铁木辛柯梁理论的解法。
在研究常截面梁、板结构的弯曲振动问题时,Li等[17-18]假设位移时提出了改进傅里叶级数法。该方法具有在模拟结构变形时更加贴近实际,结合能量原理在求解结构静变形、动态特性时[19]都具有能够快速收敛的特性。
鉴于有限单元法的计算代价较大,本文选取合适的基函数构造变截面杆的位移,并应用瑞利-里兹法求解变截面的动力学特性。为了分析变截面杆在各种经典边界条件组合下的自由振动,分别采用欧拉-贝努利梁理论和铁木辛柯梁理论进行研究。其中基于欧拉-贝努利梁理论时,首先对改进傅里叶级数中的基函数作修正,使其满足边界条件,从而得到位移函数展开的一种级数形式,利用该形式推导出杆在自由振动状态时的势能和动能,结合能量守恒原理由所得的矩阵特征值问题建立一种适应各类边界的振动分析算法。通过瑞利-里兹方法获得不同边界约束条件下欧拉-贝努利梁的固有频率。类似地,按照铁木辛柯梁理论,对不同边界圆锥形杆基于所提方法合理假设梁挠度和转角的表达式,结合能量原理把自由振动问题转化为矩阵特征值问题,即可得到铁木辛柯梁理论下的固有频率等振动特性。最后,将欧拉-贝努利梁理论下的固有频率转换为铁木辛柯梁理论下的固有频率,建立圆锥形梁的固频转化近似公式。
本文的目的是验证所提方法在欧拉-贝努利梁理论和铁木辛柯梁理论下的适用性,并对变截面锥形杆在不同边界条件下的动力学问题进行有效的求解及参数设计,为工程实践应用提供有效的参考。
1 锥形杆自由振动的理论模型
1.1 计算模型
考虑长度为L的锥形变幅杆,截面变化如图1所示,杆的横截面面积、截面对中性轴的惯性矩可分别设为
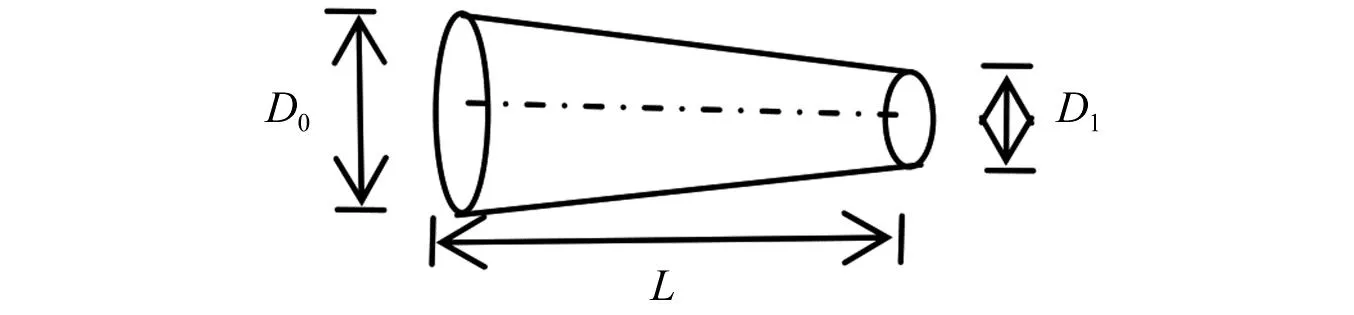
图1 圆锥形变幅杆Fig.1 A conical horn
(1)
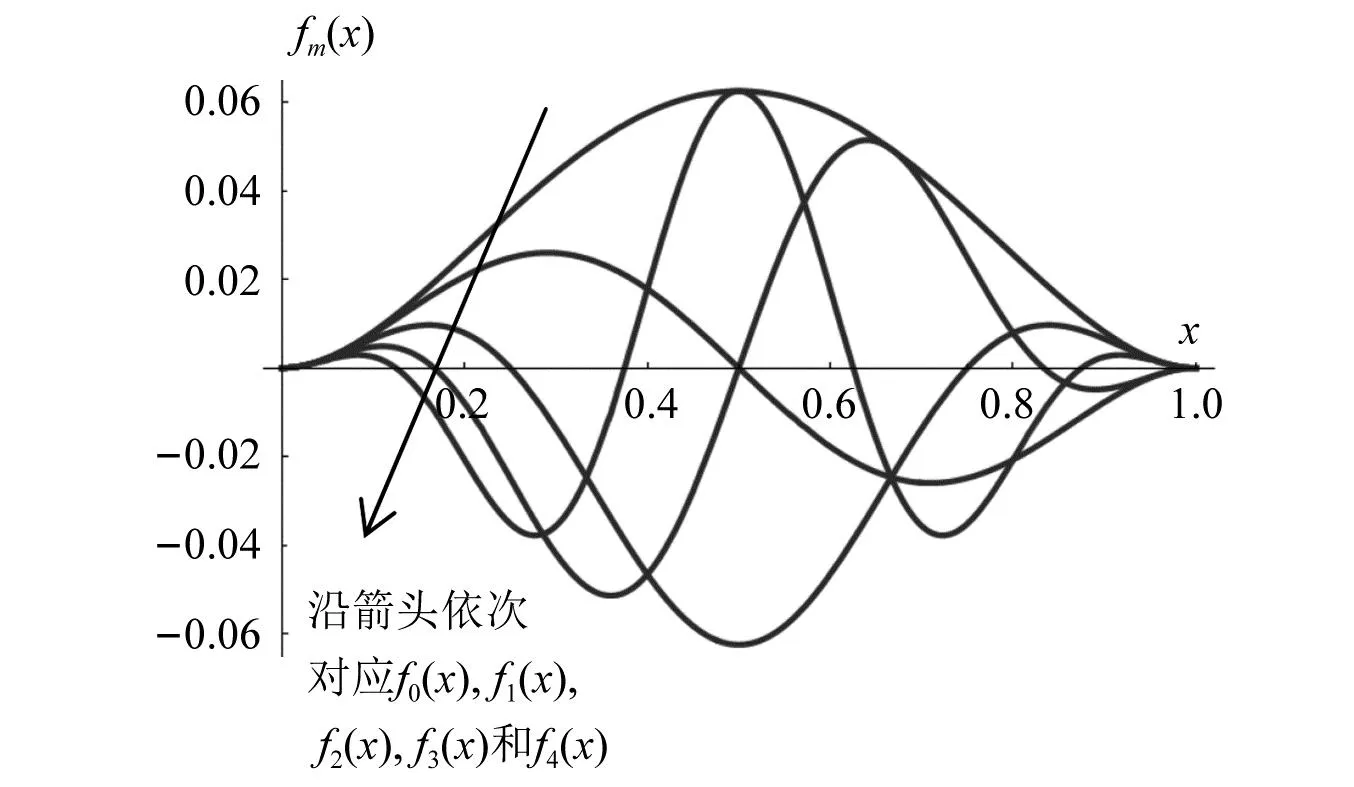
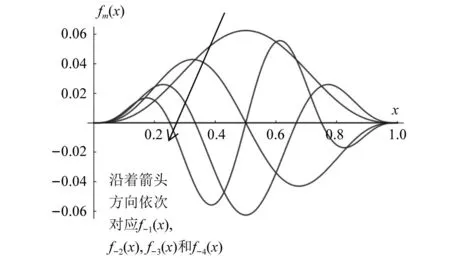
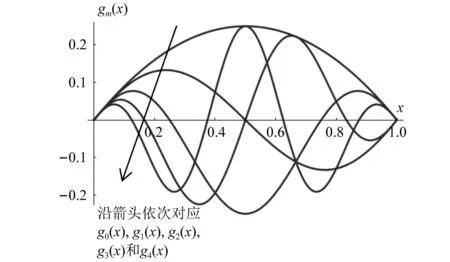
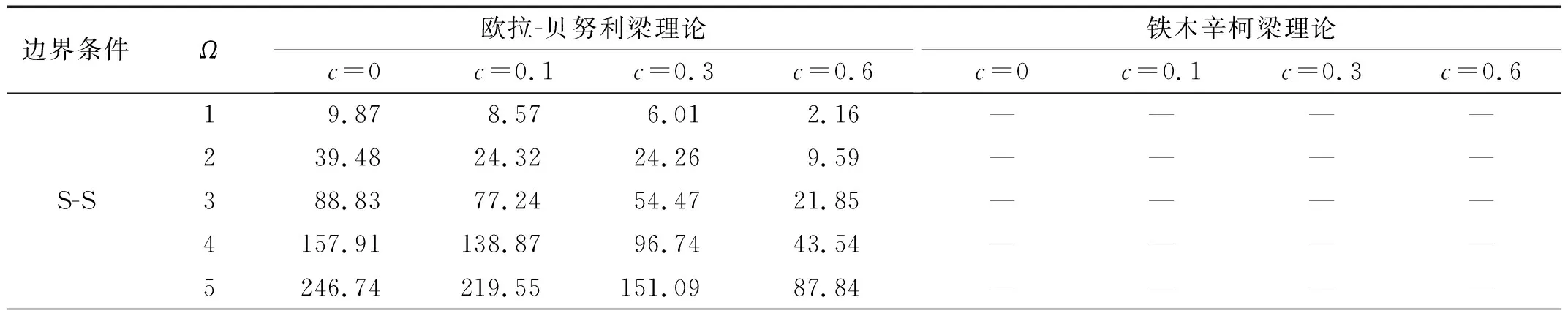
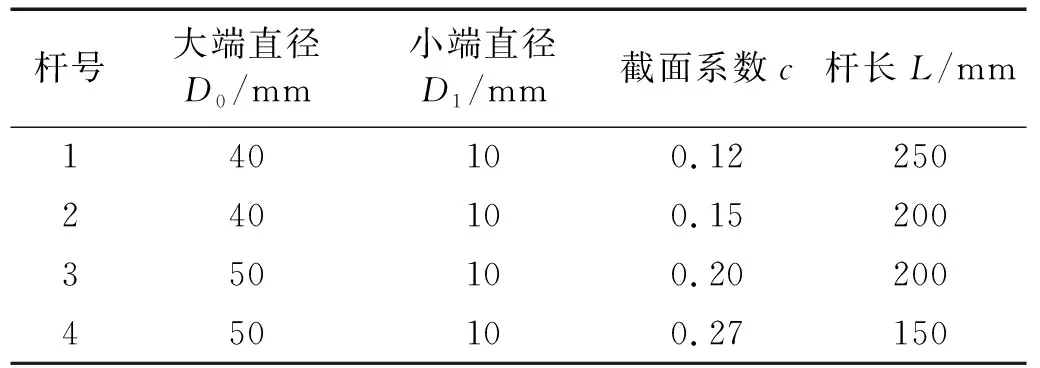
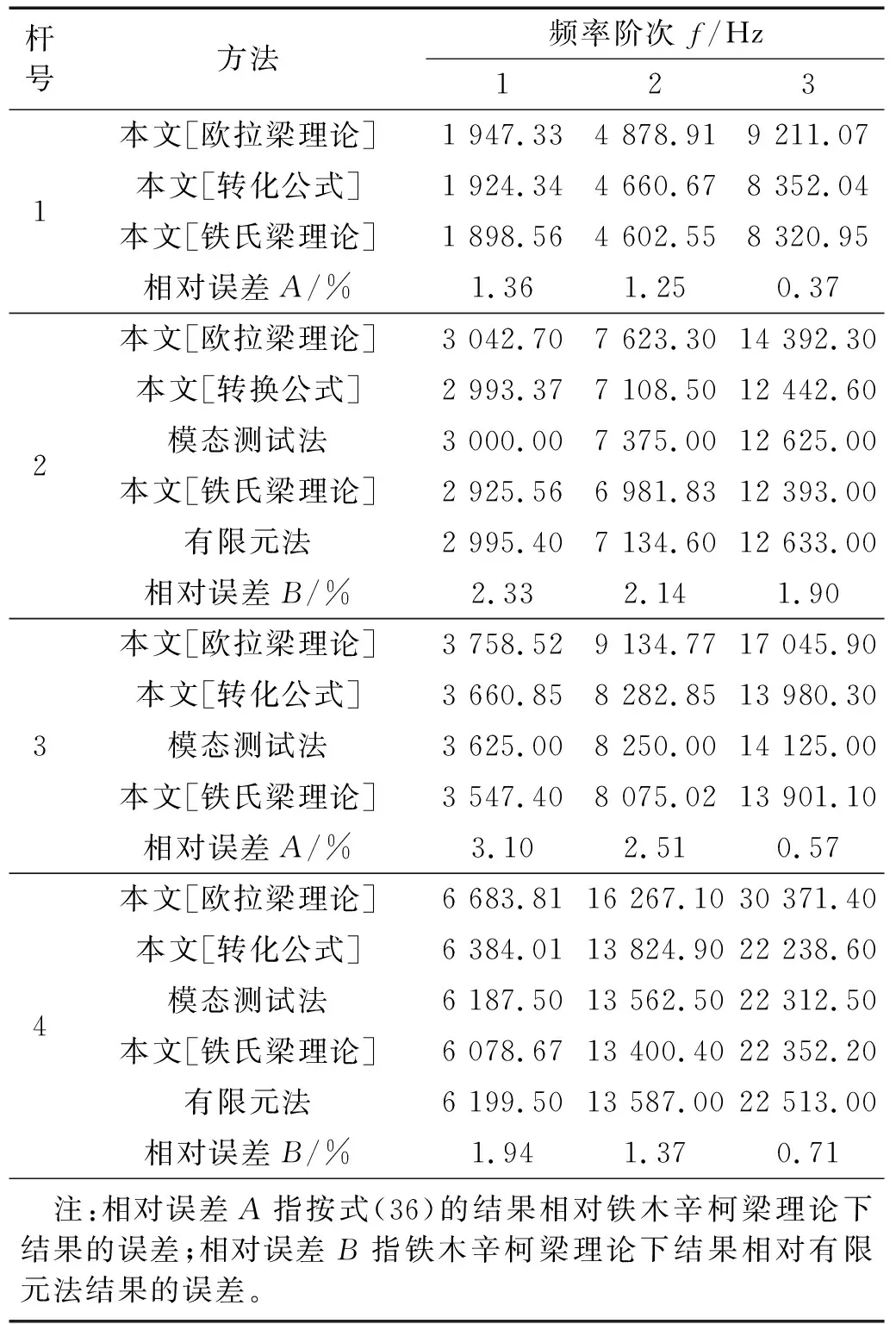
式中,c为反映截面半径变化的截面系数,c=(D0-D1)/L, 而D0,D1分别为杆左端、右端的圆形横截面直径。当c=0时,对应于等截面杆; 当0 基于铁木辛柯梁理论,变截面杆自由振动的微分方程为 (2) (3) 若研究时采用欧拉-贝努利梁理论,需忽略剪切模量的影响,对应的微分方程为 (4) 文献[20]中采用了傅里叶余弦级数与辅助正弦级数相组合而成的改进傅里叶级数,以分析欧拉-贝努利梁自由振动的位移。此类改进傅里叶级数展开的形式为 (5) (6) 为适应欧拉-贝努利梁两端的边界条件,在构造梁位移函数时笔者提出pb2-Fourier级数,所对应修正基函数fm(x)的形式如下 (7) 式中: 指数i根据左端(x=0处)的边界决定,i取的具体值为0,1,2,分别对应于自由、简支和固定边界;j根据右端(x=L)的边界决定,取值类似左端i的取值。各种边界条件下锥形杆基函数式(8)中i,j的取值如表1所示。以两端固定边界杆为例,对应弯曲位移所采用基函数fm(x)中若干基本项部分(m≥0时)和附加项部分(-4≤m≤-1时)的图像分别如图2和图3所示,其中L取1。基函数图形能够直观反映所选函数满足梁端部的边界约束条件。由式(7),附加项有4项,而图2中给出基函数中前5项基本项的图像。 表1 基函数中指数的取值Tab.1 The values chosen for the indexes in the basis functions 图2 两端固定杆Euler-Bernoulli梁模型下基函数中基本项部分的图像Fig.2 Plotting of several basic items in the basis functions for rod with two ends clamped under Euler-Bernoulli beam model 图3 两端固定杆在Euler-Bernoulli梁模型下基函数中附加项部分的图像Fig.3 Plotting of several attached items in the basis functions for rod with two ends clamped under Euler-Bernoulli beam model 则挠度函数的形式为 (8) 式(8)可适应梁两端的各种常规边界条件。 假设梁作简谐振动,有 (9) 式中: i为虚数单位;ω为圆频率。 按式(9)得变截面欧拉-贝努利理论下杆结构的弯曲势能V1为 (10) 式中:E为弹性模量;I(x)为梁截面的惯性矩。 欧拉-贝努利梁的动能为 (11) 式(9)代入式(11)得梁动能的表达式为 (12) 式中,UT为引入的函数,下标T为对应于动能。式(10)与式(12)相加,得欧拉-贝努利理论下杆结构的总能量为 EEB=e2iωtLEB=(U1-ω2UT)e2iωt (13) 将式(8)、式(10)及式(12)代入式(13),应使所得函数LEB取得极小值。需对待定系数Am求偏导并令其为零 (14) 由式(13)和式(14)得欧拉-贝努利理论下杆振动时满足的线性方程组 (K-ω2M)A=0 (15) 式中: 向量A由未知级数展开系数组成,即A=[A-4,A-3,A-2,A-1,…,Am1];K为刚度矩阵;M为质量矩阵。且矩阵K和M中元素的形式如下 (16) 式(15)有非零解的条件是系数行列式为零,对应的矩阵特征值问题为 |K-ω2M|=0 (17) 应用数值方法解出特征值,即得欧拉-贝努利理论下不同边界条件杆的固有频率。再把特征向量代入式(8),可得梁位移表达式,并得到模态。 为适应铁木辛柯梁理论下杆两端的边界条件,笔者提出此类模型下锥形杆挠度、转角函数进行改进傅里叶级数展开时,对应的基函数gm(x)的修正形式为 (18) 式中: 指数i根据左端(x=0处)的边界决定,且i取0(对应于自由)或1(对应于固定边界);j根据右端(x=L)的边界决定,取值类似左边。 以两端固定边界杆为例,式(18)中基函数基本项gm(x)对应于m≥0的部分,而基函数附加项部分对应于-2≤m≤-1的情形。其图像分别如图4和图5所示,其中L取1,图4给出基函数中前5个基本项的函数图像(m=0,1,2,3,4时)。 图4 两端固定杆在铁木辛柯梁模型下基函数中若干基本项的图像Fig.4 Plotting of several basic items in the basis functions for rod with two ends clamped under Timoshenko beam model 图5 两端固定杆在Timoshenko梁模型下基函数中附加项的图像Fig.5 Plotting of two attached items in the basis functions for rod with two ends clamped under Timoshenko beam model 则杆挠度、转角容许函数的截断形式为 (19) 式中:Am和Bn为级数展开中的待定系数;h(x)的定义同g(x);m1和n1均为截断数。 变截面铁木辛柯梁理论模型考虑了剪切变形与转动惯量对梁振动模态的影响,此时包含弯曲势能和剪切势能两部分,其表达式为 (20) 变截面梁运动时产生的动能为 (21) 梁作简谐振动时,其位移和转角的容许函数分别假设如下 (22) 式中: i为虚数单位;ω为圆频率。 类似2.3节,梁结构的总能量为 ET=e2iωtLT, 且LT=U1-ω2UT (23) 其中,U1和UT的表达式分别为 (24) 式(23)中所定义Timoshenko梁的LT函数应取极小值,即 δLT=δ(U1-ω2UT)=0 (25) 需要令LT对级数展开中系数的偏导数取零,即 (i=-2,-1,…,m1;j=-2,-1,…,n1) (26) 为方便计算,当w(x)和ψ(x)作级数展开时截断m1和n1数取相同的值N,则两者傅里叶级数截断后的项数均是N+3。 由式(26),可得铁木辛柯梁结构振动的特征频率方程,即 (27) 式中:A=[A-2,A-1,A0,…,AN];B=[B-2,B-1,B0,…,BN];Ai,Bi为改进傅里叶级数展开中的系数,具体见式(19);Ω为定义的无量纲频率,其定义见式(30)。 式(27)中刚度矩阵中各子块矩阵元素的形式为 (28) 质量矩阵中各子块矩阵元素的形式为 (29) 对式(27)对应于矩阵特征值问题,可得无量纲特征值Ωj(其中j=1,2,…,2(N+3))和相应特征值的未知系数Ai和Bi,其中由无量纲特征值对应于杆的各阶频率;再将对应的特征向量代入式(19),可得结构的相应阶模态。 在研究变截面杆固有频率的部分算例中,为使最终结果无量纲化,本文对频率作如下处理 (30) 式中:I0为杆端部截面惯性矩的较大者;A0为杆端部截面面积的较大者。 与欧拉-贝努利梁理论相比,铁木辛柯梁理论考虑剪切变形与转动惯量对梁振动模态的影响。文献[21]中介绍了一种频率的近似转换方法。本文以两端自由等截面杆为例,介绍铁木辛柯梁理论与欧拉-贝努利梁理论下固有频率之间转化关系的推导过程。 取两端自由超声变幅杆作为对象,其挠度简谐函数不妨设为 (31) 将挠度函数式(31)分别代入式(4)和式(3),得欧拉-贝努利梁理论和铁木辛柯梁理论下固有频率满足的关系式,分别如下 (32) (33) 式中:ωE为杆基于欧拉-贝努利梁理论弯曲振动的圆频率;ωT为杆基于铁木辛柯梁理论弯曲振动的同阶次固有频率。式(33)与式(32)相减得 (34) 或化为 (35) (36) 式中:fTi为基于铁木辛柯梁理论计算所得等截面直杆第i阶弯曲振动的频率;fEi为该等截面直杆基于欧拉-贝努利梁理论第i阶弯曲振动的频率。 本节给出三个算例:算例1应用两种理论,对不同截面参数、不同边界条件下的梁计算相应的无量纲频率,通过数值验证本文方法的正确性;算例2对4根锥形杆弯曲振动的固有频率进行计算;算例3中限制锥形杆的某些几何参数及已知指定阶次的目标固有频率,设计出相应的杆尺寸。 变截面直杆的具体计算参数如下:材料的密度、泊松比分别为ρ=2 500 kg/m3,ν=0.33,材料弹性模量为E=2.1×1011Pa,剪切系数κ=6(1+ν)/(7+ν)=1.089,梁长L=1 m,圆截面左端直径D0=720 mm。分别基于欧拉-贝努利梁理论与铁木辛柯梁理论,研究截面系数c对两种梁理论下梁动力特性的影响。参数c的取值为0, 0.1, 0.3和0.6,其中参数c=0时表示等截面梁。表2给出简支-简支(S-S)、固支-固支(C-C)及自由-自由(F-F)三种边界条件下变截面杆无量纲固有频率的具体取值。计算时欧拉-贝努利梁理论下的位移级数展开式(8)中一共截取了11项,对应两端简支的等截面杆的第i阶无量纲频率的解析解为Ωi=i2π2,经表2验证本文方法所得解与解析解一致(如表2中第3列S-S边界杆的无量纲频率数据9.87≈π2,39.48≈4π2等)。同样地,等截面杆在固支-固支(C-C)及自由-自由(F-F)边界条件下所得固有频率的值与振动力学教程中解析频率方程的结果一致。且应用欧拉-贝努利梁理论时,存在有趣现象:不论是否等截面杆,固支-固支(C-C)及自由-自由(F-F)边界条件下同阶次无量纲固有频率值对应相等或相近,如比较表2第3列中C-C边界杆的无量纲频率数据与F-F边界杆的无量纲频率数据,其值依次为22.37, 61.67(或61.68), 120.90(或120.91)等。这与文献[22]中的结论完全一致。 表2 变截面梁的无量纲自振频率值Tab.2 The values for non-dimensional natural frequencies of rods with variable section 参考图1,对各不同尺寸杆进行弯曲振动固有频率的计算及验证。其中杆的边界为两端自由。 圆锥杆的材料参数为:E=69 GPa,ρ=2 700 kg/m3,泊松比υ=0.33。四种圆锥形变幅杆的尺寸如表3所示。具体地:第1号杆段左、右端圆截面直径分别为D0=40 mm,D1=10 mm; 第3号杆两端圆截面的直径分别为D0=50 mm,D1=10 mm; 而第2号杆的两端直径同第1号杆; 第4号杆的两端直径同第3号杆。第1~第4号杆的长度分别为250 mm,200 mm,150 mm和200 mm。这4个杆的形状参数分别为0.100, 0.125, 0.200和0.150,其计算式为γ=(D0+D1)/(2L)。 表3 自由变幅锥形杆的形状参数Tab.3 The shape parameters for free-free conical rod 计算步骤如下:首先按式(17)得到欧拉-贝努利梁理论下锥形杆的固有频率值,然后由频率转化式(36)得到铁木辛柯梁理论下的固有频率值。另外,基于敲击法模态试验所得第2、第3、第4号杆的固有频率结果如表4所示。利用转化公式所得锥形杆前3阶固有频率的结果与铁木辛柯梁理论下固有频率值、模态测验法或有限元方法的结果均非常接近,见表4,其相对偏差在3.1%以内。表4中两种相对偏差A和B分别定义如下 表4 自由边界变幅杆前3阶固有频率的数值结果Tab.4 The numerical results for the first three natural frequencies of the conical rod (37) 式中,fi,fT,i和fFe,i分别为基于本文转化公式、本文铁木辛柯梁理论和有限元方法的计算结果。 对圆锥形变幅杆进行尺寸设计,使得其指定阶的弯曲振动固有频率达到预定值。超声变幅杆仍采用两端自由边界条件。参考图4,材料参数为E=69 GPa,ρ=2 700 kg/m3,泊松比为υ=0.33。给定杆的小端直径D1和形状系数γ,给定待设计杆指定阶次的固有频率的设计值,具体地,需设计出基频、第2阶频第3阶弯曲自振频率分别为20 kHz的圆锥形杆尺寸(其中D1=6 mm,γ=0.200)。类似的,分别设计前3阶弯曲自振频率为25 kHz的圆锥形杆尺寸(其中D1=10 mm,γ=0.250)。另外分别设计前3阶自振频率为30 kHz的圆锥形杆尺寸(其中D1=8 mm,γ=0.333)。按照尺寸和设计要求,对杆弯曲振动固有频率进行3~5次试算及修正。三种圆锥形变幅杆的尺寸按铁木辛柯梁理论设计的最终结果如表5所示。并按照欧拉-贝努利梁理论和频率转换公式对所设计尺寸的杆固有频率验证。 表5 圆锥形变幅杆的设计结果及基于Euler-Bernoulli梁理论的验证Tab.5 The designed results for the conical rod and validation by using Euler-Bernoulli beam theory 计算过程如下:首先对杆长选取一个初始值,如为50 mm或100 mm等,基于铁木辛柯梁理论按本文式(27)计算固有频率值,与待设计固有频率值比较,并调整尺寸,可得合理的尺寸设计值。另外基于欧拉-贝努利梁理论应用式(17)和频率转换公式验证所设计锥形杆的固有频率。表5表明仅基于欧拉-贝努利梁理论,未采用调整公式前,部分固有频率的结果较为接近(相对误差在5%以内),但部分结果误差很大。而按照式(36)调整后,可将欧拉-贝努利梁理论下的固有频率转换为铁木辛柯梁梁理论下的固有频率,相对误差一般在10%以内(部分可降至5%以内)。对偏大结果若按式(35)调整后,所得固频结果相对铁木辛柯梁理论下固有频率值的误差一般在5%以内。说明式(35)或式(36)可作为锥形杆设计的初步依据。 本文利用瑞利-里兹法对不同边界条件下锥形变幅杆的弯曲自由振动特性进行研究,主要结论如下: (1) 笔者在改进傅里叶级数基础上,提出一种含三角函数的新型基函数形式,该基函数在模拟杆弯曲变形时可根据杆两端边界条件直接选择对应的函数形式。 (2) 通过计算分析并与已有文献结果对比,采用所提方法基于欧拉-贝努利梁理论和铁木辛柯梁理论求解锥形杆的固有频率,验证所提方法在使用两种梁理论时均具有较好的精确度与收敛迅速等优点。 (3) 两端自由等截面杆存在两种梁理论(铁木辛柯梁理论和欧拉-贝努利梁理论)下固有频率转换的近似公式,本文应用转换公式验证了该公式在估算两端自由圆锥形杆固有频率时的可行性。 (4) 提出对给定弯曲振动频率条件下变幅杆的尺寸设计的方法,算例部分对不同边界条件下的圆锥形变幅杆进行了尺寸设计,为工程实践提供有效的参考。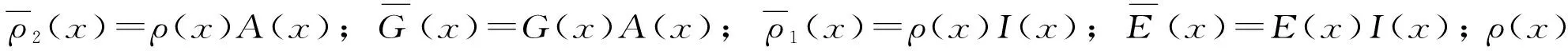
1.2 锥形杆固有频率基于欧拉-贝努利梁理论的解法
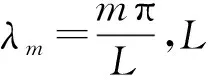
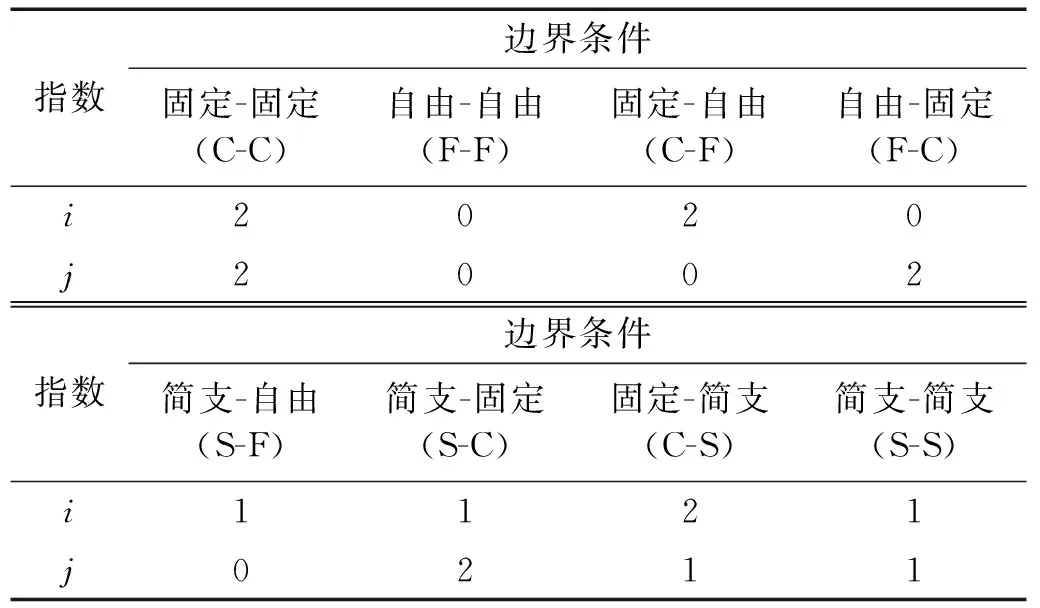

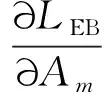
1.3 圆锥形杆固有频率基于铁木辛柯梁理论的解法

1.4 两种梁理论下固频的转换公式法

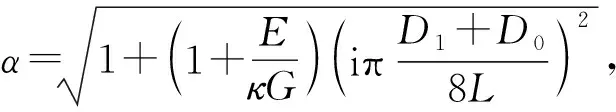
2 数值算例与分析
2.1 算例1
2.2 算例2
2.3 算例3

3 结 论

