类比法在初中数学解题中的应用技巧
赵静
【摘要】数学是抽象且逻辑关系严谨的一门学科,故而在初中数学课程中,学生经常需要解答抽象复杂的问题.为帮助学生解决问题,学好、用好数学,文章提出了结构化类比、降维类比、跨学科类比等技巧.教师应在初中数学教学中设计解决问题环节,同时指导学生应用类比法,培养学生创新解题能力,促进学生巩固学习内容,形成知识框架.
【关键词】初中数学;类比法;解决问题;应用技巧
《义务教育数学课程标准(2022年版)》在描述数学课程核心素养在初中阶段的主要表现时指出:运用归纳和类比发现数学关系与规律,提出数学命题与猜想,并加以验证.类比作为数学研究的一种经典方法,能够应用于初中数学解题中,对学生解决问题起到促进作用,能培养学生的创新意识、推理能力等.类比法在初中数学解题中的应用技巧亟待研究,教师应当在初中数学教学中,借助丰富的问题为学生搭建解题平台,同时指导学生应用类比法,使其掌握结构化类比、降维类比等技巧,活跃学生的数学解题思维.
一、类比法在初中数学解题中的应用价值
类比法是通过未知或不确定对象与已知或确定对象的归类和比较,猜测或确认未知或不确定对象的一种古老的认知思维与推测方法.在数学领域,类比法有其独特的应用价值.具体到初中数学解题方面,类比法既有助于学生梳理思路,建立解题思维,又有利于学生巩固学习内容,形成知识框架.
(一)梳理思路,建立解题思维
从小学过渡到初中阶段,学生需要面对愈发复杂的数学问题,这对学生解题思维提出了更高层次的要求.类比法作为一种古老的认知思维,对学生解题思维的建立至关重要.比如,基于类比法的归类的比较步骤,学生首先将初中数学问题划分为特定类别,其次以问题类别为依据分析解决问题的具体方法,最后根据类比得到的问题特点落实精准解题.从分析问题到解决问题,学生并非如无头苍蝇一般反复尝试,而是巧妙地在归类、比较中梳理思路,能够更加快速地建立解题思维,提升逻辑思维水平.
(二)巩固学习内容,形成知识框架
类比的本质是利用已知推理未知,这决定了类比法在初中数学解题中的应用本质———迁移已有经验探索未知答案.学生应用类比法解题,便是在不断迁移已有经验探索未知答案的过程中巩固学习内容,形成知识框架.比如在学习“直角三角形的证明”时,学生应用类比法解题,可以将“等腰三角形的证明”相关知识和经验加以应用.通过这样的解题过程,学生既能学会证明直角三角形,又能巩固“等腰三角形的证明”学习内容,明确等腰三角形与直角三角形的内在联系.
二、类比法在初中数学解题中的应用技巧
如何在初中数学解题中正确构建归类和比较关系,优化逻辑推理?下面,文章将参考北师大版初中数学教材知识结构,列举问题实例,研究类比法在初中数学具体问题中的应用技巧.
(一)结构化类比:把握问题本质,构建熟悉题型
许多学生面对初中数学题不能灵活解决问题,是因为只注重对单一问题的解题公式、定理等分析,忽略了问题之间的本质联系,没有依据题型规律建立解题模型.初中数学问题万变不离其宗,许多问题看似不同,但是深挖其本质,能够发现其题型结构高度相似.学生可按照此规律应用类比法解题,从把握问题本质入手,通过构建熟悉题型解决陌生问题,此为结构化类比.比如在“勾股定理的应用”知识领域,许多问题并非直接依托直角三角形呈现,而应用勾股定理解决问题,必须使问题满足“直角三角形”这一前提.教师可指导学生应用类比法挖掘问题的本质,将普通三角形题型转化为直角三角形题型,以便准确解题.
例题呈现 如图1所示的是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度x(罐壁厚度和小圆孔大小忽略不计)的范围是( ).
A.12≤x≤13 B.12≤x≤15 C.5≤x≤12 D.5≤x≤13
初读问题,其考查对象缺乏清晰性,联系选项再读问题,类比吸管、饮料罐底面半径、饮料罐高与直角三角形短直角边、长直角边、斜边的联系,可确认本题为勾股定理基础题型的变形,故可利用直角三角形的勾股定理特性解题.
(二)降维类比:分析已知条件,简化问题内容
降维类比是指通过对问题复杂线索与已知简单信息的对比,将复杂问题化繁为简,从而由繁到简地解题.该解题技巧在初中数学解题中的应用,要求学生细心审题,联想分析已知条件.比如在学习“弧长及扇形的面积”这部分内容时,虽然教材已经讲解了弧长及扇形面积的计算公式,但是在某些求阴影部分面积的问题中,阴影部分并非扇形,学生极易陷入解题困境.教师可指导学生应用类比法分析阴影部分的已知条件,自主将阴影部分转化为简单的图形,化简问题,简化解题.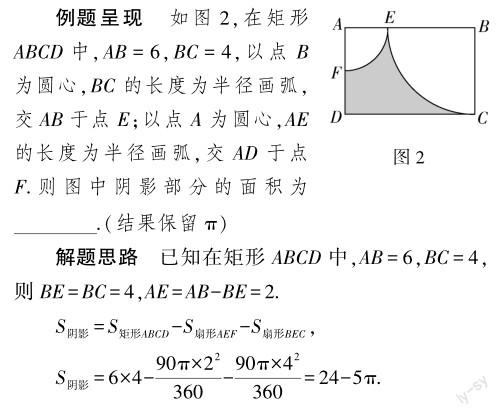
初看示意图,图中阴影部分为不规则图形,无法直接代入任何面積公式.结合已知信息展开类比,示意图整体为矩形,空白处为一大一小两个扇形,故而可将阴影部分转化为矩形与两个扇形的面积差.
复杂问题与简单信息同时出现时,简单信息可为复杂问题提供解题思路,学生可在解题过程中,类比简单信息与复杂问题,将复杂问题简单化,简化解题过程.以本题为例,复杂问题为阴影部分面积,简单信息为矩形面积与扇形面积.经过降维类比,充分分析已知条件,找准化繁为简的切入点,问题简单化,代入公式轻松解决问题.
(三)跨学科类比:应用非数学元素,发散解题思维
根据《义务教育数学课程标准(2022年版)》,义务教育数学课程特别设计跨学科主题活动,意在培养学生跨学科的应用意识与实践能力.跨学科是指将数学学科与其他非数学学科相联系,发散学生思维,使其将数学知识广泛运用在学习、生活中,同时迁移其他学科知识理解数学问题,跨学科类比由此成为类比法在初中数学解题中的应用技巧之一.教师在指导学生应用类比法解决初中数学问题时,应当避免局限在数学元素的归类、对比中,应使学生大胆应用非数学元素与数学元素的类比,实现创新解题.比如在“一次函数的应用”知识领域,许多问题为路程问题,学生可联系物理学科“平均速度的测量”等学习经验,类比分析路程问题,发散求解.
例题呈现 从地面垂直向上抛射一个物体,在落地之前,物体向上的速度v(m/s)是运动时间t(s)的一次函数.经测量,该物体的初始速度(t=0时物体的速度)为25m/s,2s后物体的速度为5m/s.(1)写出v,t的函数表达式.(2)经过多长时间后,物体将到达最高点?(此时物体的速度为0).
(2)解:已知物体到达最高点时速度为0,则0=-10t+25,解得t=2.5.
答:经过2.5s后,物体将到达最高点.
类比数学元素与非数学元素,本题与物理中“平均速度的测量”相关.假设物体做平抛运动,其速度与时间仍存在函数关系,即v=kt+b.从地面垂直向上抛射的物体符合平抛运动特征,物体在下落的过程中不断减速,可直接设v-t关系式为v=kt+b.紧接着,运用“两点式”求解函数关系式,将(0,25)(2,5)分别代入v=kt+b,可得到k与b的具体数值,解得v=-10t+25.最后根据题意,将v=0代入v=-10t+25,得到物体到达最高点的时间.
本问题体现了初中数学跨学科应用与实践理念,满足跨学科类比解题技巧在初中数学解题中的应用条件.细心审题会发现问题隐含的非数学元素,大胆联想,在物理知识与数学解题中建立通道,在物理层面还原“平抛运动”v-t图像,是类比解题的重要保障.学生可使图像跃然纸上,也可根据头脑中的图像记忆提炼函数关系式.此后,代入数学元素于函数关系式,学生可融合类比法与一次函数核心知识,高效解题.
(四)“数”“形”类比:运用数形结合思想,化抽象为直观
数形结合是初中数学解题的“法宝”.古今中外,无数数学家提出数形结合思想.数学问题的解决过程中,数是重要依据,形是关键工具.初中数学函数、方程、不等式、立体几何等问题中,学生均可运用数形结合思想解决问题,此为“数”“形”类比.学生可根据问题已知条件化“数”为“形”或以“数”化“形”,从而化抽象问题为直观信息,提高解题效率.比如在学习“应用一元一次方程———追赶小明”知识时,学生若无法凭借问题文字信息理清解题思路,便可应用“数”“形”类比技巧,将问题文字转化為图形语言,以具象化的方程关系帮助解题.
例题呈现 小彬和小强每天早晨坚持跑步,小彬每秒跑4m,小强每秒跑6m.(1)如果他们站在百米跑道的两端同时相向起跑,那么几秒后两人相遇?(2)如果小强站在百米跑道的起点处,小彬站在他前面10m处,两人同时同向起跑,几秒后小强能追上小彬?

答:小彬站在小强前面10m处,两人同时同向起跑,5秒后小强能追上小彬.
类比问题第(1)小问与图3,小彬和小强同时相向起跑,两人相遇,即共同跑完100米,可根据“路程和=速度和×时间和”等量关系,列出方程“(4+6)x=100”解题.类比问题第(2)小问与图4,小彬和小强一前一后同时同向起跑,小强追上小彬时,小彬跑步的距离与两人跑步起点距离之和,等于小强跑步的距离,等量关系隐含在示意图中,可列出方程“4y+10=6y”并解题.
本题为典型的相遇追及问题,共分为两个小问,学生若仅凭文字信息分析问题,极易落入解题陷阱,混淆一元一次方程的应用思维.学生若应用类比法,将文字信息类比为图形语言,即图3与图4,有助于将小彬和小强的相遇、追及关系具象化,把握等量关系,列出方程并解题.学生可结合题意应用类比法,通过图形表现归类和比较结果,从而快速判断等量关系,保证列方程、解方程的准确性.
结 语
基于类比法在初中数学解题中的应用价值,类比法在初中数学解题中的应用技巧已经成为教师关注的焦点.类比法在初中数学解题中的具体应用,可以是把握问题本质,构建熟悉题型,也可以是分析已知条件,简化问题内容,还可以是应用非数学元素,发散解题思维,更可以是运用数形结合思想,化抽象为直观.教师应当在初中数学课程中,积极指导学生应用类比法解决问题,使学生建立良好的解题思维,达成高效学习、学以致用.
【参考文献】
[1]唐美依.“类比法”让初中数学解题教学提质增效[J].数学之友,2022,36(23):16-17.
[2]贺湘雲,赖冬梅.类比法在初中数学教学中的应用[J].学周刊,2022(35):61-63.
[3]段发一.类比思维在初中数学解题教学中的应用[J].数理天地(初中版),2022(16):33-35.

