数学推理的可视化教学策略

唐红霞

东北师范大学史宁中教授认为，学生的数学核心素养有抽象、推理和建模。其中，抽象主要是引导学生从生活到数学的横向数学化过程，而推理主要是引导学生在数学的世界中进行符号的生成、重塑和被使用。通过数学的抽象、数学的推理，引导学生充分经历横向数学化和纵向数学化，进而建构有意义、有价值的数学模型。数学推理类型是丰富的，形式是多样的，它不仅包括演绎推理，也包括合情推理。其中，合情推理可以分为归纳推理和类比推理，归纳推理包括完全归纳推理和不完全归纳推理。在小学数学教学中，教师要借助可视化手段、策略等引导学生的推理，助推学生的推理，借助学生的数学观察、猜想、证明等活动，让学生的推理具有合理性、合情性、逻辑性等品质。

可视化教学的手段是丰富的，主要包括图形的可视化、动作的可视化、语言表达声音的可视化等。可视化教学能有效启迪学生的合理猜想，启发学生的直觉思维，引导学生进行推理。借助可视化教学，能让学生的思维触手可及，让学生的认知有据可查。作为教师，要善于借助可视化图形，将抽象的数学直观地确证与表征出来，以便引发学生推理、引导学生推理。借助可视化图形引导学生推理，其根本依据是学生的认知、感性的思维、独特的心理等。

例如，教学《圆的周长》这一部分内容时，学生依据《圆的认识》学习内容中的“画圆”操作，能有效推出“圆的大小与圆的半径或者直径有关”。因为，圆规两个脚张开得越大，画出的圆也就越大，圆规的两个脚展开越小，所画出的圆也就越小。而圆规两个脚之间的距离就是圆的半径。为了进一步优化学生的数学猜想、验证学生的数学猜想，教师可在教学中借助下图创设可视化的情境，引导学生猜想：圆的周长大约是直径的多少倍？

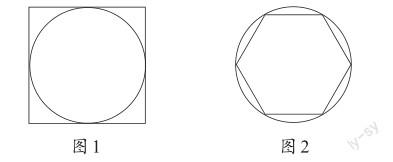
借助图1，学生能直观地进行逻辑猜想、推理：正方形的边长是圆的直径，正方形的周长是边长的四倍，圆在正方形的里面，圆的周长比正方形的周长小，所以圆的周长应该是直径的四倍少一些；借助图2，学生能在其中增添一些辅助线，采取同样的演绎推理，有效地推理、猜想出圆的周长应该是直径的三倍多一些。通过这样的可视化图形，可以引导学生给圆的周长和直径的倍数关系科学设定一个阈限，即圆的周长应该是直径的三倍多一些、四倍少一些，进而为学生有效进行圆的周长实验、圆的周长实验数据的演算，以及圆的周长和直径的关系的精确性探究，奠定坚实的基础。

可视化图形是学生数学推理可视化的重要策略。在小学数学教学中，教师要善于建构可视化图形，用可视化图形激发学生的猜想、催生学生的推理。图形是学生推理的依据、证据，它能有效激活学生的推理思维、催生学生的推理想象，让学生的推理从模糊走向清晰、走向精准。

在小学数学教学中，教师可以通过可视化操作、可视化动作等为学生搭建数学推理的支架，引导学生基于可视化操作进行数学推理。小学生的数学推理不同于成人的數学推理，他们往往需要借助一定的媒介、以一定的操作作为支撑，展开一种准逻辑性或半逻辑性的推理。作为教师，要尊重学生的半逻辑性甚至非逻辑性的推理，同时要以学生的可视化操作引导其推理，继而增强学生的推理感受、体验，让学生的推理更深刻、更有效。

例如，教学《平行四边形的面积》这一部分内容时，有的学生猜想平行四边形的面积等于底乘斜边，因为他认为，平行四边形可以推拉成长方形，而长方形的长相当于平行四边形的底，长方形的宽相当于平行四边形的斜边，长方形的面积等于长乘宽，所以平行四边形的面积等于底乘斜边。据此，教师引导学生展开具体直观的操作。学生通过操作，能亲身感受、体验到平行四边形在推拉成长方形的过程中面积发生了变化。在该学生否认了自我的迷思概念、相异构想以及毫无根基的数学推理的基础上，教师引导学生用剪拼法操作。首先将平行四边形沿高剪开，分成两个直角梯形或一个直角梯形与一个直角三角形，然后拼接成一个长方形。在学生操作的基础上，教师引导学生思考、推理：平行四边形在剪拼成长方形的过程中，面积有没有发生变化？长方形的长相当于平行四边形的什么？长方形的宽相当于平行四边形的什么？长方形的面积怎样算？所以平行四边形的面积可以怎样计算？通过这种类似数学推理中的“三段论”的方式，可以引导学生自主建构、创造平行四边形的面积公式。通过可视化操作，学生深刻地认识到，图形面积的转化前提是图形的等积变形。只有在“等积”的前提下进行图形的面积推理，图形的面积推理才是有效的。

可视化操作不仅仅是学生数学推理的一种手段、方式，也是学生数学推理的重要组成。作为教师，要不断地寻找证据、捕捉证据，为学生的数学推理开辟更多的可能性空间。此外，可视化操作既可以为学生的数学推理提供引子，激发学生的数学推理，也可以直接助推学生的数学推理。借助可视化操作，学生的数学推理能更合理、更科学、更有效、更精准。

可视化教学手段主要诉诸学生的感知，这种感知不仅包括学生的视觉感知、触觉感知，也包括听觉感知。在引导学生数学推理的过程中，语言的声音表达同样是一种可视化手段。在小学数学教学中，教师可以引入信息技术，充分利用其声色光影，助推相关的语言表达。换言之，语言表达可以是纯粹的话语声音，也可以借助其他相关的辅助手段，让可视化语言表达更丰富、更生动、更有说服力。

例如，教学《多边形的内角和》这一部分内容时，教师放手让学生探究四边形的内角和、五边形的内角和等，并让学生用语言表述自己的探究过程。在探究四边形的内角和时，有的学生还沿袭三角形的内角和的探究方法，用剪拼法、折角法、量角法等展开探究；在探究五边形的内角和时，不少学生发现折角法、剪拼法等已经不能有效探究其内角和了。同时，很多学生也认为用量角法探究多边形的内角和误差太大。因此，学生开始转变思路。有的学生认为，可以将多边形转化成若干三角形；有的学生认为，可以从多边形的一个顶点开始将这个多边形分成若干三角形，然后借助三角形的内角和探究多边形的内角和。据此，学生从四边形开始探究，并用语言积极表述。如：“四边形可以分成两个三角形，因为每个三角形的内角和都是180°，所以四边形的内角和就是180°乘2”“五边形可以分成三个三角形，因为每个三角形的内角和是180°，所以五边形的内角和就是180°乘3”，等等。通过学生的语言表达，他们能快速进行推理：六边形的内角和应该是180°乘4，一百边形的内角和应该是180°乘98，进而学生类比推理出“n边形的内角和是（n-2）×180°”。

可视化语言是可视化教学的重要组成部分。作为教师，要引导学生进行语言表达，让学生在数学推理过程中学会数学表达。数学表达能助推学生的数学推理，而数学推理则能让学生的数学表达更严谨、更精准。

总之，可视化教学手段是学生数学推理的重要支撑。在小学数学推理教学中，教师要丰富可视化教学手段，以此激发学生的推理意识、提升其推理能力、优化其推理品质、丰富其推理样态，充分发挥可视化教学手段的育人功能，助推学生数学推理素养的全面发展，彰显其育人价值。

（作者单位：山东省沂源县沂河源学校）

（责任编辑金灿）