基于WOA-BP算法的氟金云母钻削工艺参数优化*

戴春雨,马廉洁,2,孙德谦,李红双,陶其赫

(1.东北大学机械工程与自动化学院,沈阳 110819;2.东北大学秦皇岛分校控制工程学院,秦皇岛 066004)

0 引言

氟金云母陶瓷作为一种典型工程陶瓷,具有优良的机械性能、抗冲击性、热震性,兼具无机非金属材料的物理和化学性能[1-2],在国防航空航天、核能、生物医疗等领域拥有广阔的应用前景[3-4]。由于可加工陶瓷材料的硬脆性,在加工中会导致材料去除率低并且由于材料组织内部的硬相,会对刀具造成反切削作用,加剧刀具磨损,出现孔口崩边、裂纹等现象导致表面加工质量差,降低陶瓷工件在使用过程中的可靠性[5-6]。目前关于可加工陶瓷的研究主要集中在材料制备技术、可加工性能、加工机理等方面,对材料去除和刀具磨损建立最优工艺参数的研究相对较少。因此选择合理的切削参数和刀具角度分析钻削参数对钻削性能的影响,并且使用优化设计方法得到最佳工艺参数,对实现可加工陶瓷的高效加工及延长刀具的使用寿命有着重要的意义[7-9]。

鲸鱼优化算法(whale optimization algorithm,WOA)作为一种新的群智能优化算法,依赖关键参数少,拥有较强全局搜索性能[10-11]。已经成功应用于车间调度、函数优化、图像识别等各种行业[12-13]。在对工程陶瓷的算法建模中,应用较多的是一些传统的算法,例如遗传算法、粒子群算法等[14-15],对于WOA算法应用的报道较为少见。BP神经网络(back propagation)预测效果良好,但是在预测精度方面仍有较大的提升空间。为了进一步提高预测的精确度,可以利用WOA优良的求解性能,针对BP神经网络存在的收敛速度慢、易陷入局部最优和网络不稳定等缺点进行改进[16-18],可获得预测精度更高的网络模型,实现氟金云母陶瓷钻削加工过程中工艺参数的建模与优化。

本文以氟金云母陶瓷钻削加工实验为基础,通过建立的WOA-BP神经网络预测模型,建立了钻削加工材料去除率、刀具磨损率与切削速度vc、钻头顶角ω、刃倾角λs的一元模型和多元模型。利用鲸鱼优化算法对双目标参数优化模型进行求解,得到了一组最优工艺参数,并进行了验证实验,结果表明得到的最优参数是合理的。

1 实验

选用氟金云母可加工陶瓷作为实验材料,其形状为圆柱形,尺寸为51×10 mm。材料主要性能参数为:体积密度为2.5～2.8 g/cm3,维氏硬度为850～900 HV,热导率为2.1 W/(m·K),弯曲强度为108 MPa。钻头选用直径φ=1.5 mm的YG6X硬质合金钻头,钻头角度一致。切削实验在XD-40A型立式铣床上进行,无冷却,实验中保持恒定的轴向载荷,分别以切削速度vc、顶角ω、刃倾角λs为变量进行单因素试验,如表1所示。并进行正交试验,如表2和表3所示。切削结束测量加工所用时间、钻孔直径和钻孔深度计算材料去除量,用DSX110型3D激光共聚焦显微镜测量钻头主后刀面平均磨损宽度作为刀具磨损量。

表1 单因素实验条件

表2 正交实验因素水平

表3 正交实验条件

机加工中的基本要求是降低加工成本,提高生产效率。从实际生产要求出发,以实验测得的工件材料去除量V与所用加工时间t的比值作为材料去除率M的量化指标,以刀具磨损量Vb与工件材料去除量的比值作为刀具磨损率φ的量化指标,较低的刀具磨损率代表产生单位体积的刀具磨损时,可去除的材料多,刀具性能优良,可加工性强。

V=π(d/2)2hn

(1)

φ=Vb/V

(2)

式中:d为钻孔直径,h为钻孔深度,n为钻孔数量。

2 基于WOA算法改进BP神经网络

2.1 WOA改进BP神经网络算法模型

BP神经网络作为一种误差逆向传播训练的多层前馈神经网络,其学习效果和收敛速率主要由初始权值、阈值的选择决定,比较合理的初始权值、阈值能够加快网络模型收敛速度并且获得最优解。不合适的权值和阈值可能会导致其网络收敛速度缓慢,容易陷入局部极小值,还会出现过拟合等问题。WOA算法通过设置最佳搜索代理和随机代理的方式实现种群位置的更新,其优点在于原理简单,可调整的参数少,寻优能力强。根据收缩包围机制、螺旋泡网捕食、随机搜索猎物3种方式来进行寻优,即在鲸鱼群捕食猎物的过程中,每只鲸鱼有3种行为,一种是收缩包围猎物,所有的鲸鱼都向着当前最优位置前进;一种是泡网捕食,鲸鱼环形收缩游动喷出气泡来驱赶猎物。在每一代的迭代更新中,鲸鱼种群会随机选择这两种行为来进行捕猎。但在鲸鱼进行包围猎物的行为中,部分鲸鱼将会随机选择一只鲸鱼作为自己的目标,并向其靠近,实现随机搜索猎物的目的,因此具有较强的局部搜索和全局勘探能力。

采用WOA算法改进BP神经网络建立预测模型,将BP神经网络预测误差作为WOA算法适应度值,对不满足适应度条件的进行WOA算法的收缩包围机制、螺旋泡网捕食、随机搜索猎物操作,进而迭代更新,当适应度值满足条件要求时,将寻优结果作为BP神经网络的最优权值和阈值,来改善单一BP神经网络的不足,WOA算法改进BP神经网络流程图如图1所示。

图1 WOA改进BP神经网络流程图

2.2 BP神经网络结构参数设置

将单因素实验数据中的切削速度vc、钻头顶角ω、刃倾角λs作为输入参数,将材料去除率和刀具磨损率作为输出参数。选择单隐藏层的BP神经网络,其中输入层结点为3,输出层结点为1,隐藏层结点根据经验公式来确定,如式(3)所示,由此可知隐藏层结点个数的有效范围为[3,12],在此范围内进行试验并挑选出最优值对网络进行训练,预测数据的均方误差随着隐含层神经元个数变化曲线如图2所示。当神经元个数为7时,均方根误差最小,为0.010 97所以选择隐含层神经元个数为7。

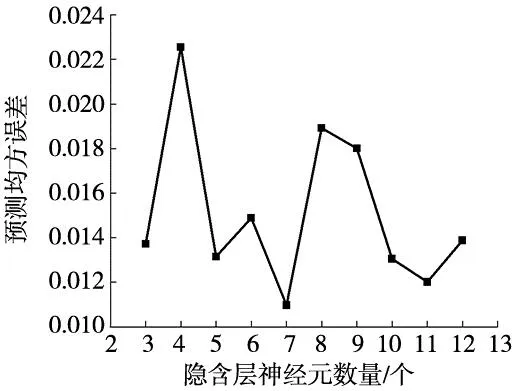
图2 均方误差随不同隐含层神经元个数变化曲线

(3)

式中:l表示隐藏层结点个数,m为输入层结点个数,n为输出层结点个数,a为[1,10]之间的任意整数。

经过多次训练后的神经网络模型其他的主要参数设置为:输入神经元为3,输出层神经元为1,学习率为0.01,迭代最大次数为1000,误差目标为10-6,隐含层传递函数为tansig函数,输出层传递函数为purelin函数。WOA算法设置为:种群规模为40,进化次数为500次。

3 基于WOA-BP一元建模

3.1 工艺参数对材料去除率的影响

将单因素实验数据传递至网络中,利用搭建好的WOA-BP神经网络进行预测,以获得足够的离散数据样本,结合实验值和预测值数据样本,利用最小二乘法对离散数据进行拟合建模。

图3给出了切削速度对材料去除率的影响曲线,曲线可以分为3个阶段,当切削速度小于14.13 m/min时,材料去除率随切削速度增加而上升,这主要是由于切削速度增加,钻头获得的扭矩增加,切削力增大,切削能力得到增强。当切削速度在14.13 m/min和18.84 m/min之间时为第2阶段,此时材料去除率为下降趋势,主要由于切削速度增大,刀具磨损的速度加快,影响了刀具的切削能力。当切削速度大于18.84 m/min时材料去除率又呈现上升的趋势,因为切削速度的持续增大加强了切削能力,此时刀具磨损对切削过程的影响占次要地位。由3个阶段的变化趋势,可建立材料去除率关于切削速度的一元模型,此模型以正弦函数为基础,由于图像具有左右不对称性,因此在正弦函数项前乘以二次项加以修正,加上常量来提高拟合度,提出的一元模型如下:

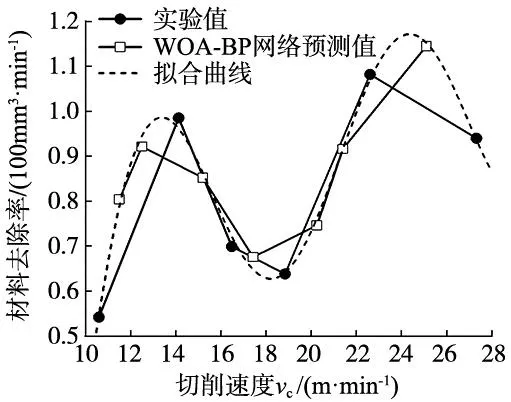
图3 切削速度对于材料去除率的影响

通过最小二乘法求解得到模型如式(4)所示。

(4)

式中:M表示材料去除率,vc为切削速度,模型相关系数R2=0.991 8,表明曲线拟合度较高模型具有较高的精度。

图4给出了顶角对材料去除率的影响曲线,曲线可以分为3个阶段,当顶角小于100°时,随着顶角的增大,钻头主切削刃长度减小,当轴向压力一定时,切削刃上的应力增大,切削能力加强。当钻头顶角超过100°的临界值时,尽管切削刃上的应力在增大,但同时磨损也在加剧,使切削能力下降。当顶角超过130°时,切削刃磨损的影响不在占主导地位,材料去除率又升高。根据图4所示的离散点变化趋势可建立材料去除率关于刀具顶角(ω)的一元模型,其模型如式(5)所示。

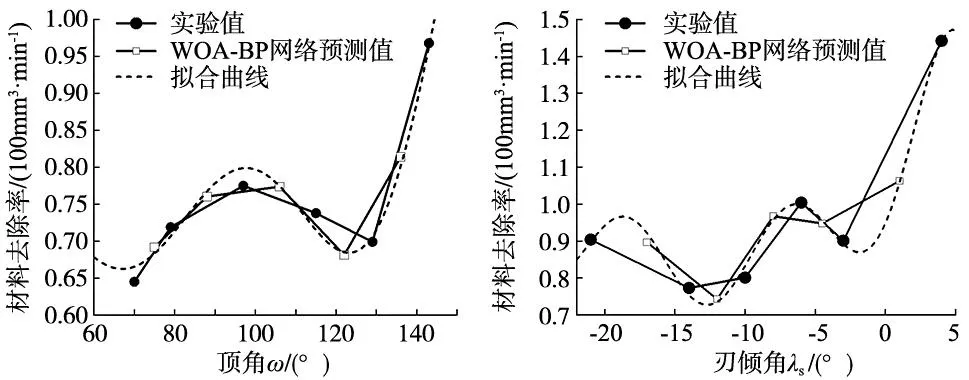
图4 顶角对于材料去除率的影响 图5 刃倾角对于材料去除率的影响

M(ω)=(0.00009888ω2+0.01492ω-0.4533)×
sin(0.06717ω+13.02)+0.7599

(5)

式(5)模型相关系数R2=0.973 0。

图5给出了刃倾角对材料去除率的影响曲线,曲线可以分为两个阶段,当刃倾角在-21°和-13°之间时,材料去除率呈下降趋势,主要由于随着刃倾角数值的减小,钻头的横刃变短,轴向压力一定时切削刃所受应力减小,切削能力下降,材料去除率有所降低。第2阶段当刃倾角大于-13°时,此时刃倾角的减小使切削刃变得更加锋利,去除材料变得更加容易,所以曲线整体呈上升趋势。根据图5所示的离散点变化趋势可建立材料去除率关于刀具刃倾角(λs)的一元模型,其模型如式(6)所示。

(6)

式(6)模型相关系数R2=0.993 4。

3.2 工艺参数对刀具磨损率的影响

图6给出了切削速度对刀具磨损率的影响曲线,整体趋势为刀具磨损率随切削速度增大而增加。当切削速度小于14.13 m/min时,此时主轴转速低,切削扭矩较小,处于低速磨损阶段。当切削速度在14.13 m/min和22.61 m/min之间时,刀具切削能力增强,处于稳定磨损阶段。当切削速度大于22.61 m/min时,刀具切削力矩增大,造成刀具快速磨损。由3个阶段的变化趋势,可建立刀具磨损率关于切削速度的一元模型,得到的一元模型如式(7)所示。

图6 切削速度对于刀具磨损率的影响

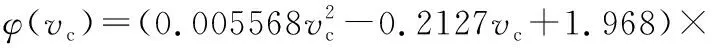
(7)

式(7)模型相关系数R2=0.982 0。

图7给出了顶角对刀具磨损率的影响曲线,曲线可以分为3个阶段,当顶角小于80°时,随着顶角的减小,刀具的磨损由横刃沿切削刃向刀尖延伸,靠近横刃处的切削刃磨损严重。当顶角大于130°时,刀具的磨损由刀尖沿主切削刃向横刃延伸,靠近刀尖处切削刃磨损严重,所以这两个阶段的刀具磨损率曲线呈现增加趋势。当顶角处于80°和130°之间时,切削刃全长参与切削,刀具磨损率曲线呈现差值较小的正常波动。根据图7所示的离散点变化趋势可建立刀具磨损率关于刀具顶角(ω)的一元模型,其模型如式(8)所示。

图7 顶角对于刀具磨损率的影响 图8 刃倾角对于刀具磨损率的影响

φ(ω)=(0.0000905ω2-0.02106ω+1.16)×
sin(-0.07745ω-0.623)+0.2923

(8)

式(8)模型相关系数R2=0.991 4。

图8给出了刃倾角对刀具磨损率的影响曲线,曲线可以分为两个阶段,当刃倾角在-21°和-8°之间时,刀具磨损率呈下降趋势,因为此时切削刃工作长度逐渐增加,切削过程中应力分布均匀。第2阶段当刃倾角达到临界值-8°时,切屑的排出不流畅,增加了切削刃与切屑接触的时间,造成刀具磨损加剧,曲线整体上呈现上升趋势。根据图8所示的离散点变化趋势可建立刀具磨损率关于刀具刃倾角(λs)的一元模型,其模型如式(9)所示。

(9)

式(9)模型相关系数R2=0.991 9。

4 多元模型建立与求解

4.1 多元模型假设

4.1.1 材料去除率多元模型假设

基于材料去除率单因素拟合结果(式(4)～式(6)),合并同类函数项,不同类函数项相乘,加常数项,整合得到氟金云母材料去除率关于工艺参数的多元模型为:

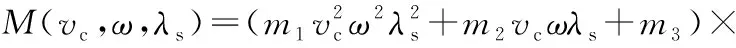
(10)

式中:m1～m6均为常数,由氟金云母陶瓷和YG6X钻头的材料属性共同决定。

4.1.2 刀具磨损率多元模型假设

基于刀具磨损率单因素拟合结果(式(7)～式(9)),合并同类函数项,不同类函数项相乘,加常数项,整合得到氟金云母刀具磨损率关于工艺参数的多元模型为:

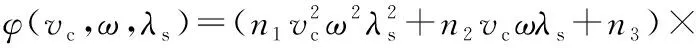
(11)

式中:n1～n6均为常数,由氟金云母陶瓷和YG6X钻头的材料属性共同决定。

4.2 多元模型求解

将多元模型计算值与正交试验值的方差最小作为适应度函数(见式(12)),利用12组正交试验(第1,2,4,5,6,8,9,10,12,13,14,16组,见表3)结果,用WOA算法对多元模型进行求解优化,经过求解后的材料去除率和刀具利用率多元模型如式(13)和式(14)所示。

(12)

式中:Ai为多元模型计算值,Ait为正交试验值。

(13)

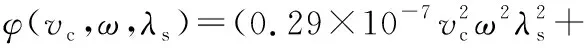
(14)

4.3 多元模型精度检验

利用4组正交验证实验(第3,7,11,15组)对多元模型进行检验,计算实际值与模型计算值的相对误差,如表4所示。由结果可知,相对误差基本在10%以内,表明建立的多元模型具有较高精度。

表4 相对误差 (%)

5 双目标优化

在实际生产加工过程中,期望在尽可能提高切削效率的同时,尽可能减小刀具磨损量,以获得较好的加工质量。基于材料去除率和刀具磨损量的多元模型,可建立双目标优化模型:

F1=max(M(vc,ω,λs))
F2=min(vc,ω,λs)
vc=9.42～23.55 m/min
ω=80°～130°
λs=-20°～5°

(15)

通过WOA算法可对双目标优化模型进行求解。在构建适应度函数时,因刀具磨损率取最小值,材料去除率取最大值,二者取向相反,所以将材料去除率取倒数,得到算法的适应度函数:

(16)

通过WOA算法最终求解得到优化参数如下:vc=18.89 m/min,ω=105.14°,λs=-12.76°,具体迭代过程如图9所示。以上参数带入式(13)和式(14)中,获得对应的材料去除率和刀具磨损率为:M=104.52 mm3/min、φ=0.23 μm/10mm3。此时刀具磨损率较小,切削效率较高,得到的参数合理。

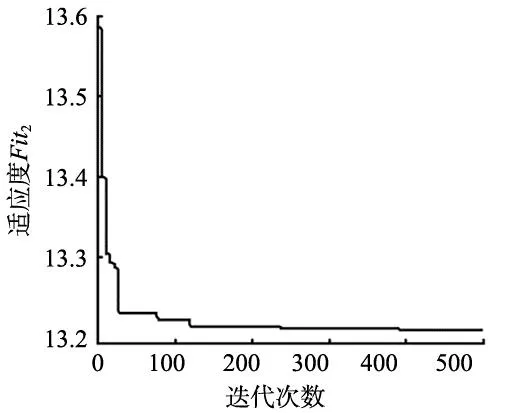
图9 适应度迭代过程图

基于获得的最优工艺参数进行验证实验,验证实验的参数调整为:vc=18.89 m/min,ω=106°,φs=-13°,进行两次重复实验,实验结果如图10所示,通过实验获得对应的材料去除率和刀具磨损率分别为:M=113.27 mm3/min、φ=0.25 μm/10mm3。相对误差分别为7.74%和8.69%。可以得出经过优化后的工艺参数实验结果较好,材料去除率得到提高,刀具磨损率有所减小,证明经过WOA算法优化求解得到的工艺参数较为合理。

图10 YG6X钻头磨损形貌

6 结论

(1)基于WOA-BP神经网络的预测值和单因素实验值,利用最小二乘法,建立了材料去除率和刀具磨损率关于工艺参数的一元模型,模型的相关系数均在0.97以上,拟合精度较高。

(2)提出多元模型,并利用WOA算法对多元模型中的未知系数进行求解。验证实验的相对误差在10%以内,表明模型具有较高的可靠性。

(3)以最小刀具磨损率和最大材料去除率进行双目标优化,得到的最优工艺参数为:vc=18.89 m/min,ω=105.14°,λs=-12.76°,此时材料去除率较大,刀具磨损率较小,M=104.52 mm3/min,φ=0.23 μm/10mm3。

(4)对最优工艺参数进行实验验证,对应的材料去除率和刀具磨损率相对误差分别为7.74%和8.69%,证明该优化结果较为合理。