基于神经网络参数自学习的阻抗控制*

党选举,袁以坤

(桂林电子科技大学电子工程与自动化学院,桂林 541004)

0 引言

随着电子信息技术的发展,机器人被广泛用于各种重复性高的作业场景。如基于力控制的机器人打磨,其具有高效性、高精度、稳定性好、安全性高等特点[1]。对于机器人的力控制,普遍采用阻抗控制方法。阻抗控制将机器人末端与环境之间的力与位置联系起来,通过末端的作用力反馈调整末端位置实现力的控制[2-3]。传统的阻抗控制在刚度固定的平面环境下效果显著,但对于刚度变化和环境位置未知的情况效果不理想。

为了能够让阻抗控制能够适应复杂未知的环境,国内外学者一直致力于阻抗控制的改进研究。WEI等[4]考虑到机器人末端位移的误差对力的影响,基于模型自适应的方法补偿末端位置,从而实时调整末端位置以实现恒力的控制,但它需要调整的参数过多,参数的选取是否合适对于系统的影响很大。李德昀等[5]引入自适应模糊滑模控制器补偿时间延时估计产生的估计误差,抵消动力学模型中的非线性因子和不确定因素对系统的干扰。XU等[6]提出了一种基于动态神经网络的自适应阻抗控制方法,用于多物理约束下的冗余机器人,为了在环境模型未知的情况下提供最佳接触性能,提出了一种自适应阻抗学习方法,以实现机器人与环境之间的最佳交互。LORIS等[7]基于阻抗控制方法,设计了一种模型预测控制器,利用Q学习方法对于模型预测控制器求解,然后在线优化阻抗参数。张世玉等[8]提出一种改进型自抗扰阻抗控制策略。该策略通过自抗扰控制器生成新期望力,调整机器人末端工具坐标系的位置,实现精确的力跟踪。

上述文献从参考位置误差、时间延时产生的误差、阻抗参数不合适、期望力误差等方面对传统阻抗控制方法进行改进,实现了对力的控制,但设计的方法,在控制系统的动态性能,有待进一步提高。本文在自适应阻抗控制的基础上,设计了调节参数神经网络自学习的阻抗控制算法,通过机器人末端力反馈信息,结合神经网络在线学习,实时最优阻尼参数,适应复杂未知的接触环境,实现了打磨过程中力的有效控制。

1 阻抗控制系统分析

1.1 机器人环境动力学模型

为了研究整个打磨系统,需将机器人与环境看作一个动态系统来建模分析。一般情况下,工具末端与打磨器件的环境动力学模型可以表示为:

(1)

式中:Fe表示工件与机器人末端的作用力,Be、Ke分别表示环境的阻尼和刚度参数,X和Xe分别表示工具的实际位置和环境表面的位置。

由于机器人末端移动速度缓慢,环境模型可以简化为“弹簧”模型,该模型由机器人末端、环境位移和环境接触面的作用力之间的关系表示:

(2)

1.2 阻抗控制误差分析

阻抗控制是建立接触力和位置的动态关系模型,并通过调节阻抗模型参数改变其动态特性,确保机器人在环境中能够表现出良好的柔顺性。阻抗控制可以看作是质量-阻尼-弹簧模型:

(3)

式中:Xe为环境位置,X为机械臂末端实际位置,Md、Bd、Kd分别代表目标阻抗模型的惯性、阻尼和刚度,Fe为末端接触力,Fd为期望力。阻抗控制框图如图1所示。

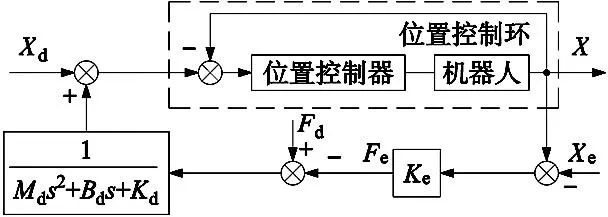
图1 阻抗控制框图

为了简化后续计算,对式(3)进行拉普拉斯变换得出式(4)。

(4)

假设机械臂在工作过程中,忽略机器人内环位置控制对于系统的影响,计算机械臂末端实际力与期望力之间的差值ef,则:

ef=Fd-Ke(X-Xe)=Fd+KeXe-Ke[Xd+h(s)ef]

(5)

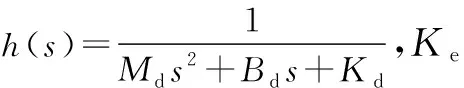
将式(5)进一步化简:

(6)

当机械臂在稳定状态下运行时,速度和加速度的大小均看成0,由此可得机械臂末端接触力跟踪的稳态误差为:

(7)

式中:keq目标阻抗和环境的等效刚度参数。

(8)

则可知机械臂与环境的实际接触力的大小为:

(9)

由上式可知,机械臂末端的实际接触力大小F是参考轨迹Xd和期望接触力Fd的函数。当参考轨迹Xd满足如下表达式:

(10)

从式(10)可知,当接触力稳态误差ess=0时,需准确获得接触面的环境位置Xe和刚度大小Ke,进而计算出参考轨迹Xd。

但在实际打磨加工过程中,工件的刚度和环境位置难以精确获取,得到的实际接触力并非期望接触力,因此需要进行位置调节。机械臂在实际打磨加工过程中,被加工工件的刚度一般较大,较小的位置误差也会带来较大的接触力稳态误差,并且加工环境一般都是未知可变的,实际接触力难以精确跟踪期望接触力,这将直接影响打磨效果。

为了解决在未知环境下,环境参数变化引起的打磨力精度问题,通过构造神经网络自适应地修正参数,实时跟踪环境刚度变化和位置变化,实现对期望力的精准控制。

2 基于神经网络参数自学习的阻抗控制

2.1 阻尼自适应的阻抗控制

阻抗控制中可以通过调整惯性、阻尼、刚度参数使机器人适应环境参数,由于固定的参数只能适用于一种固定环境,对于刚度变化或复杂曲面环境力误差大跟踪能力差。动态的调整阻抗控制参数可以使机器人的动态特性适应环境的变化,保证系统的稳定性和减小稳态误差。WEI等[9]采用阻尼自适应阻抗控制,基于参考模型自适应得出李雅普诺夫函数,通过稳定性证明得出阻尼补偿量ΔB(t)与ΔX、ΔF的函数关系。

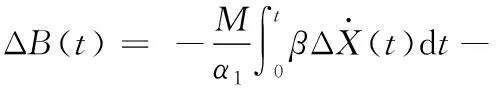
(11)

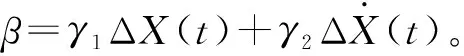
阻尼自适应的阻抗控制相比传统的阻抗控制性能有所提高,但是对于曲面环境的收敛能力还是不足并且超调过大。

2.2 基于神经网络参数自学习的阻抗控制

式(11)揭示阻尼参数受多因素及多因素组合影响,表现出阻尼与多因素特征之间的关系。

将式(11)化简得:

(12)

式中:ω1、ω2、ω3、ω4为调节参数。

根据式(12),本文基于影响阻尼补偿的多种因素构建调节参数神经网络,通过神经网络在线学习式(12)中的调节参数,使得阻尼补偿参数达到最优,从而使阻尼参数在不同打磨环境下保持最优,其中激励函数反映了阻尼变化多因素特征,结构如图2所示。选取神经网络的多个激励函数如式(13)所示。

图2 阻尼自适应中用于调节参数神经网络

(13)

图2中3层神经网络由输入层、中间层、输出层构成,将影响阻尼补偿的因素设置为激活函数,调节参数为权重,通过神经网络自学习调整权重,该神经网络的前向传播为式(12)。

将神经网络的性能指标函数设置为:

(14)

基于梯度下降法,由于每个权重在整个系统中的占比不同,其重要程度不同。本文采用了独立设置学习率的方法,在每个权重调整中设置单独的学习率参数更新为:

(15)

式中:η为学习率,α为动量因子。

整体的系统框图如图3所示,将当前位置和速度信息作为神经网络输入信号,神经网络实时计算出的阻抗参数传入阻抗控制器,进而计算出末端位置增量,通过位置到力的变换,实现对于力的控制。

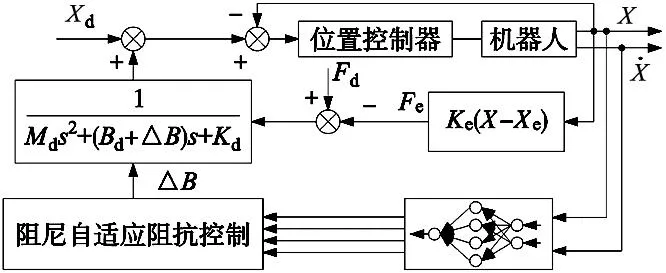
图3 调节参数神经网络系统框图

3 仿真验证

在仿真实验中,只需要考虑末端位置与力的关系,将六自由度机器人简化为二自由度[10]如图4所示。

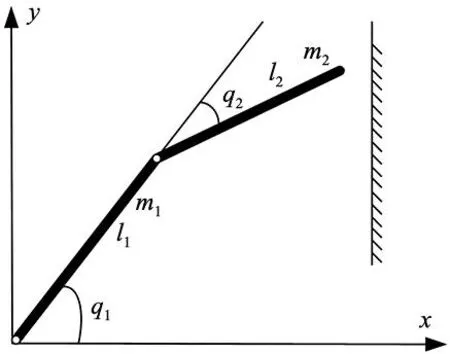
图4 二自由度机器人与环境接触模型

采用文献[11]中的机器人模型,其中,取l1和l2为1 m,m1=10 kg,m2=5 kg。位置环PID控制的比例参数kp=85 000,积分参数ki=120和微分参数kd=85。设置初始参考位置为0.866 m,在各个环境中设置阻抗参数的初始值均为Md=[1 1]Bd=[90 90]Kd=[50 50]。本文提出的神经网络参数自学习算法中的学习率η在以下范围内选取都能实现未知环境下力的有效跟踪,η1∈[0.3,0.5],η2∈[0.3,0.5],η3∈[0.2,0.4],η4∈[0.6,0.9]。本次仿真设置学习率为η=[0.5 0.5 0.35 0.9],动量因子α=0.5。

为了与经典的阻抗控制,甘亚辉等[10]提出的自适应变阻抗控制对比,通过恒力跟踪仿真实验和动态力跟踪仿真实验,验证本文所提的调节参数神经网络自学习的阻抗控制在不同环境下的力跟踪能力。

3.1 恒力跟踪仿真实验

恒力跟踪仿真实验模拟多种不同环境,分别是环境刚度突变的平面、环境刚度固定的斜面、环境刚度固定的曲面、环境刚度突变的曲面及刚度动态变化的曲面环境。设置期望力Fd=30 N。

(1)在接触面为平面环境下,验证在刚度突变时,所提出的算法是否具有鲁棒性,Ke的变化如式(16)所示。

(16)

测试结果如图5所示,图中显示各控制算法的力跟踪效果。从图中得知,传统的阻抗控制和自适应阻抗控制的超调太大,并且存在一定的稳态误差,本文提出的算法超调明显降低,稳态误差明显减小。

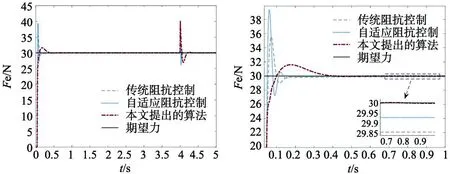
(a) 环境刚度突变接触面为平面的力跟踪效果 (b) 环境刚度为6000 N/m时力跟踪效果

(2)在接触面为斜面的环境下,刚度Ke=8000 N/m,验证效果如图6所示。从图中可以看出本文提出的算法超调小,无稳态误差。

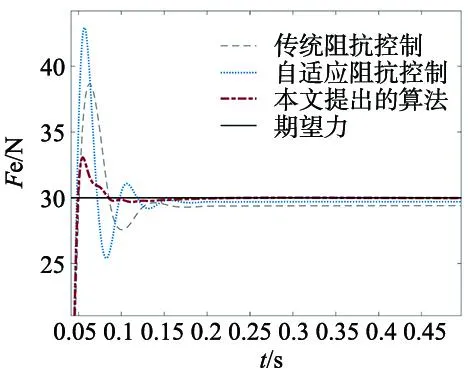
图6 刚度固定接触面为斜面的力跟踪效果

(3)在接触面为曲面环境下,刚度固定Ke=8000 N/m,测试结果如图7所示。从图中得知,传统的阻抗控制和自适应控制都有不小的超调,并且有明显的稳态误差。

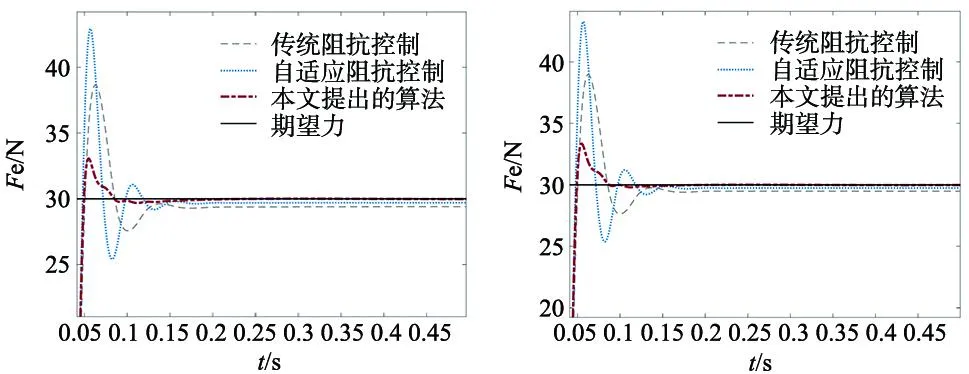
图7 刚度固定接触面为曲面的力跟踪效果 图8 环境刚度接触面同时变化时力的跟踪效果

(4)在接触面和刚度同时正弦变化的环境下,力跟踪效果图如图8所示。

图8中传统阻抗控制方法和自适应阻抗控制方法的超调都过大,有明显稳态误差。

由上述实验可得出如下结论:对于刚度固定的平面环境,传统阻抗控制和自适应控制都能够达到预期的力跟踪效果,但是超调都过大。对于斜面或是更为复杂的曲面而言,传统阻抗控制和自适应阻抗控制都存在一定的稳态误差,并且在控制过程中超调过大。而本文提出的控制方法,在这些环境中都可以达到预期的控制效果实现柔顺控制。具体参数比较如表1所示。表中σ为超调量,ess为稳态误差,单位N。

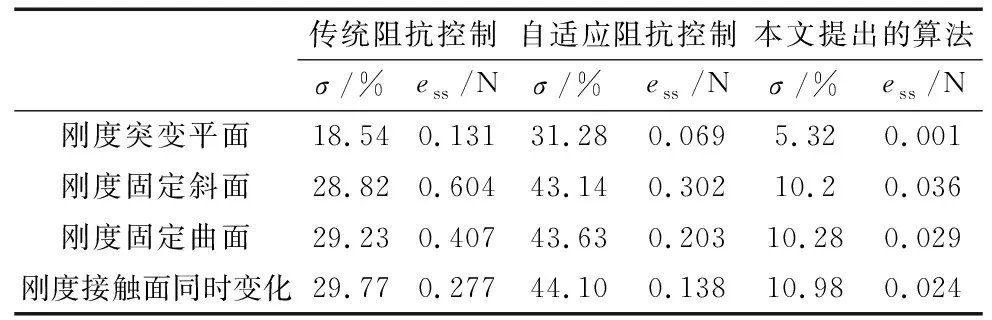
表1 各种算法在不同接触环境下的恒力跟踪效果

通过数值比较,本文提出的算法相比传统阻抗控制,在刚度突变的平面环境稳态误差降低了99.23%,动态性能超调量下降了13.22%,刚度固定斜面环境,稳态误差下降低了94.03%,超调量下降了18.62%,刚度固定曲面环境,稳态误差下降低了92.87%,超调量下降了18.95%,刚度接触面同时变化环境,稳态误差下降低了89.16%,超调量下降了18.79%。

3.2 动态力跟踪仿真实验

在实际打磨过程中还存在力变化情况,模拟3种力变化情况,分别是:

(1)期望力突变,初始期望力Fd=30 N,运行4 s后期望力突变Fd=40 N。

(2)期望力斜坡增长,Fd=30+2*tN。

(3)期望力正弦变化,Fd=25+5*sin(t) N。

各个算法在以上环境中的控制效果如图9～图11所示。从图中得知,传统阻抗控制和自适应阻抗控制在力跟踪方面都存在不足,系统动态性能有很大超调和一定的稳态误差,相比本文提出的算法超调小,稳态误差几乎为0,力跟踪能力更优。具体参数如表2所示。

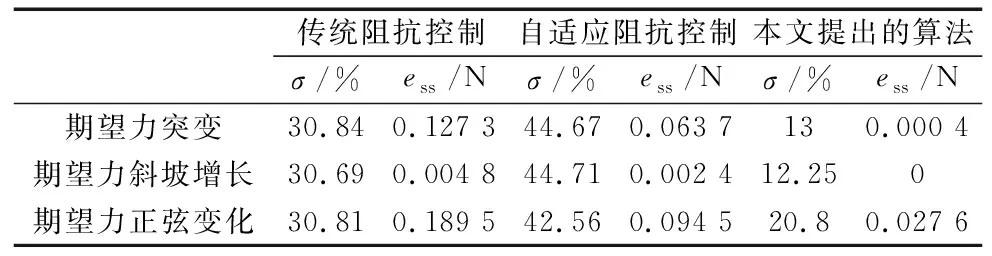
表2 各种算法在动态期望力下的力跟踪效果

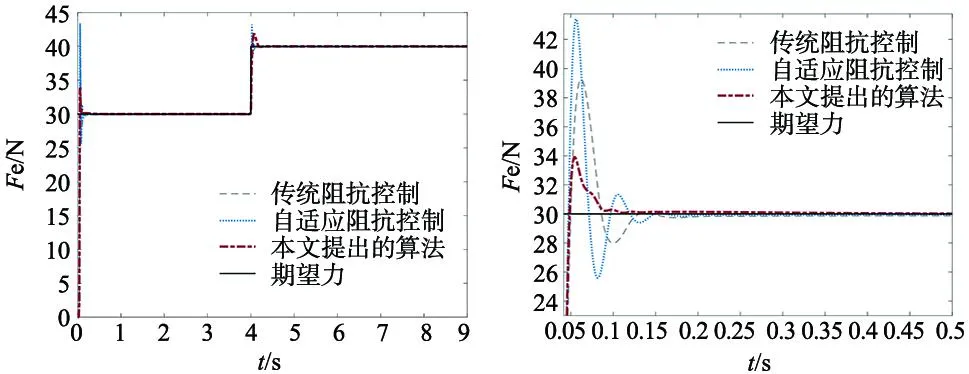
(a) 固定刚度突变期望力的力跟踪效果 (b) 期望力30 N力的力跟踪效果

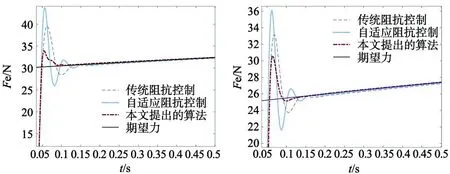
图10 固定刚度斜坡期望力的力跟踪效果 图11 固定刚度正弦期望力的力跟踪效果

4 结论

为了解决工业机器人打磨中环境刚度变化或接触面未知情况下机器人难以实现打磨有效的力跟踪问题,本文提出了一种控制参数神经网络自学习的阻抗控制方法。仿真结果表明,对刚度变化环境、环境位置变化环境和变力跟踪等情况,相比于传统的阻抗控制方法,本文所提出的算法提高了打磨系统的稳定性和鲁棒性,降低了系统的超调和稳态误差,能有效地实现力控制。