数控轧辊磨床圆柱度三点测量原理及仿真分析*

曾祥礼,吴怀超,赵丽梅,杨 绿

(贵州大学机械工程学院,贵阳 550025)

0 引言

圆柱形零件广泛应用于各行各业,如电力工程、化工和造纸行业[1],数控轧辊磨床中的轧辊作为典型的圆柱形零件,在各行各业中占着举足轻重的地位。随着我国制造产业的发展,对产品的质量要求越来越高,迫使数控轧辊磨床朝着高精度、高速、高效等方面发展,如何高效、高精度地测量轧辊这类轴类零件的圆柱度误差已经成为了国内外研究的热点[2]。

形状误差对数控轧辊磨床的精度有着很大的影响,其中圆柱度误差能全面反应出轧辊表面的形状误差,圆柱度形状误差由被测轧辊各截面圆度误差、截面最小二乘圆心和截面半径差组成[3-4],在对轧辊圆柱度进行测量时,存在直行(导轨)和回转(回转轴)两个测量基准[5-6],传感器采集的信号中含有被测轧辊截面的轮廓信息和两个基准的运动误差,如何把两个基准的运动误差从传感器采集的信号中分离出来是实现轧辊圆柱度测量的关键一步。

误差分离技术应用于很多领域,包括轴类零件的圆柱度测量[7],国内外研究人员对圆柱度测量过程中产生的主轴回转误差、直行导轨误差以及截面圆度误差的正确分离做了大量研究[8],洪迈生等[9]应用三点法分离回转轴回转误差,但是分离出的回转轴回转误差与各截面最小二乘圆心偏心运动叠加,如何将两者分离,文中并没有提及。李东升等[5]利用反向法分离除了导轨的轨迹误差,但是文中并没有分离出回转轴的回转误差,得到的截面圆度误差并不准确。目前国内数控轧辊磨床圆柱度的测量几乎都采用两点离线测量,测量精度低下,不能从多维角度反应测量的精度,测量数据也不能参加程序的计算[10],严重影响工作效率。

为了解决这些问题,现把误差分离技术应用到数控轧辊磨床圆柱度的测量,提出一种数控轧辊磨床三点圆柱度误差分离方法,对其分离过程进行数学推导,根据数学推导过程建立测量数学模型,基于MATLAB进行仿真,成功分离出各个截面圆度误差、各截面之间的半径差和各截面最小二乘圆心初始位置,同时还成功分离出了回转轴的回转运动误差和导轨的轨迹误差。

1 三点数控轧辊磨床圆柱度测量原理

被测轧辊各截面圆度误差、截面最小二乘圆心和截面半径差不仅是组成轧辊圆柱度的3部分,在对轧辊的圆柱度进行测量时,传感器采集的信号中也包含以上3部分,同时还包含了回转轴的回转误差和导轨的直行误差,有效分离出这几部分才能进一步通过一定的方法对轧辊圆柱度误差进行评定。

1.1 被测轧辊各截面圆度误差

在对轧辊任意截面c测量时,截面c的轮廓可以看成是以2π为周期变化的复杂封闭曲线,根据傅里叶所提出的任何周期性函数都可以写成傅里叶级数的特性,轧辊第c个截面的圆轮廓可以用离散傅里叶级数形式表示[10]:

(1)

以3个传感器的轴线交点为坐标原点建立测量坐标系Oc-XcYcZc(Zc垂直于XcYc平面,图中未画出)。

设O为绝对坐标系的坐标原点,且U轴与工作台回转轴线平均线重合(U垂直WV平面,图中未画出),圆度测量原理如图1所示。

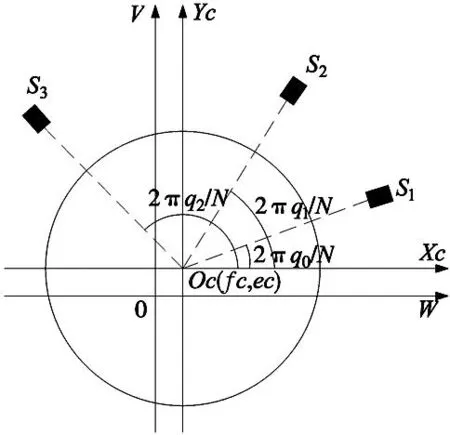
图1 三点法圆度测量原理图

由图1可以看到测量时,传感器S1、S2、S3固定,分散在待测轧辊周围,轧辊随着工作台一起转动,传感器就会获取被测截面的轮廓信息和回转运动误差。传感器S1、S2、S3在测量点i(第c号截面上)采集的数据用s1c(i)、s2c(i)、s3c(i)来表示[11],则:

s1c(i)=nc(i+q0)+λcx(i)cos(2πq0/N)+
λcy(i)sin(2πq0/N)

(2)

s2c(i)=nc(i+q1)+λcx(i)cos(2πq1/N)+
λcy(i)sin(2πq1/N)

(3)

s3c(i)=nc(i+q2)+λcx(i)cos(2πq2/N)+
λcy(i)sin(2πq2/N)

(4)

式中:nc(i)为c截面的轮廓信息,λcx为回转运动误差在x方向上的运动分量,λcy为回转运动误差在y方向上的运动分量。

设z0、z1、z2为传感器的输出信号的权值系数,snc为3个传感器输出信号的加权和,则:

snc(i)=z0s1c(i)+z1s2c(i)+z2s3c(i)

(5)

把式(2)～式(4)带入式(5)中,得:

snc=z0nc(i+q0)+z1nc(i+q1)+z2nc(i+q2)+
λcx(i)[z0cos(2πq0)+z1cos(2πq1/N)+z2cos(2πq2/N)]+
λcy(i)[z0sin(2πq0)+z1sin(2πq1/N)+z2sin(2πq2/N)]

(6)

为了消除回转误差的影响,使:

z0cos(2πq0/N)+z1cos(2πq1/N)+z2cos(2πq2/N)=0

(7)

z0sin(2πq0/N)+z1sin(2πq1/N)+z2sin(2πq2/N)=0

(8)

式(7)和式(8)为只有两个方程的三元一次方程组,明显可知权值系数z0、z1、z2(权值系数均不为0)存在无数解,为减小计算,取z0=1,式(7)×sin(2πq1)-式(8)×cos2πq1,整理得权值系数z1、z2表达式如式(9)和式(10)所示。

(9)

(10)

将z0=1及其式(1)、式(9)、式(10)代入式(6)得:

snc(i)=nc(i+q0)+z1nc(i+q1)+z2nc(i+q2)=

Bchsin[2πh(i+qt)]}

(11)

因为被测截面的圆度误差中并不包含被测截面轮廓傅里叶级数的一阶谐波分量[12],结合式(1)可知,在测量坐标系中被测轧辊第c个截面的圆度误差vc(i)可以表示为:

(12)

因此,式(11)可以表达为:

(13)

对式(13)做离散傅里叶变换,再利用离散傅里叶变换的时延相移性质可得:

(14)

式中:Snc(k)、Vc(k)分别为snc(i)、vc(i)离散傅里叶表达变换式,U(k)为三点法误差分离权函数。

U(k)=z0e2πkq0m/N+z1e2πkq1m/N+z2e2πkq2m/N

(15)

对式(14)做离散傅里叶逆变换,可得被测截面c分离回转误差后的圆度误差vc(i),则:

vc(i)=IDFT[Vc(k)]

(16)

1.2 被测轧辊各截面最小二乘圆心

被测轧辊截面圆度误差不包含被测截面轮廓傅里叶变换的一阶谐波分量[12],结合式(12),可以把式(2)改写为:

nc(i)=vc(i)+A1ccos(2πi/N)+B1csin(2πi/N)

(17)

由于nc(i)、vc(i)都是周期性序列,则:

nc(i+q1)=vc(i+q1)+A1ccos[2π(i+q1)/N]+
B1csin(2π(i+q1)/N)

(18)

nc(i+q2)=vc(i+q2)+A1ccos[2π(i+q2)/N]+
B1csin(2π(i+q2)/N)

(19)

将式(18)、式(19)带入式(3)、式(4)中得:

s2c(i)=vc(i+q1)+A1ccos[2π(i+q1)/N]+

B1csin[2π(i+q1)/N]+λc(i)cos(2πi/N)

cos(2πq1/N)+λc(i)sin(2πi/N)sin(2πq1/N)

(20)

s3c(i)=vc(i+q2)+A1ccos[2π(i+q2)/N]+

B1csin[2π(i+q2)/N]+λc(i)cos(2πi/N)

cos(2πq2/N)+λc(i)sin(2πi/N)sin(2πq2/N)

(21)

联立式(20)、式(21)化简为:

λc(i)cos(2πi/N)+A1ccos(2πi/N)+B1csin(2πi/N)=

(22)

λc(i)sin(2πi/N)-A1csin(2πi/N)+B1ccos(2πi/N)=

(23)

式中:等式右边的被测截面c的圆度误差vc(i+q1)、vc(i+q2)以及传感器的输出s1c、s2c皆为已知序列,现在用W1c、W2c分别表示式(22)、式(23)右边,则:

λc(i)cos(2πi/N)+A1ccos(2πi/N)+B1csin(2πi/N)=W1c

(24)

λc(i)sin(2πi/N)-A1csin(2πi/N)+B1ccos(2πi/N)=W2c

(25)

联立式(24)、式(25),令W1c×sin(2πi)-W2c×cos(2πi)化简得:

W1csin(2πi)-W2ccos(2πi)=A1csin(4πi)-B1ccos(4πi)

(26)

让式(26)两边同时乘sin(4πi/N)并在一个周期内求和得:

(27)

所以可得轧辊任意被测截面c离散傅里叶级数的一阶谐波分量余弦系数:

(28)

同理,让式(26)两边同时乘cos(4πi)并在一个周期内求和得:

(29)

整理可得轧辊任意被测截面c离散傅里叶级数的一阶谐波分量正弦系数:

(30)

根据最小二乘原理,在测量坐标系中被测截面c的最小二乘圆心(ac,bc)为:

(31)

(32)

由式(31)、式(32)可以看出,被测截面c最小二乘圆心的位置也就是截面c轮廓傅里叶级数的一阶谐波分量的系数(A1c,B1c)。

将式(24)×sin(2πi/N)-式(25)×cos(2πi/N)可以得到被测截面c的回转误差:

λc(i)=W1c(i)cos(2πi/N)+W2c(i)sin(2πi/N)-
A1ccos(4πi/N)-B1csin(4πi/N)

(33)

至此能得到被测轧辊截面c的最小二乘圆心的位置和轧辊回转轴线的回转误差。

1.3 被测轧辊各截面之间的半径差

(34)

(35)

1.4 导轨的轨迹误差

当测量装置回转轴旋转时,由3个传感器所确定的测量坐标系与直行导轨之间的距离是恒定的,因此在测量坐标系中,由被测各截面的坐标原点所形成的空间曲线与直行导轨是平行的。根据坐标平移原理可以得到:

λcu(i)=fc+λc(i)cos(2πi/N)

(36)

λcv(i)=gc+λc(i)sin(2πi/N)

(37)

实际测量时,会使绝对坐标系O-UVW的W坐标轴与测量系统的回转轴线平均线尽可能重合,满足这一条件,在被测轧辊截面测量一周内,被测截面回转运动误差在坐标轴OU、OV上的回转运动分量λcu、λcv在一个回转周期内取平均值应为0,即:

(38)

(39)

对式(36)、式(37)两边在一个回转周期内取平均,可得:

(40)

(41)

若以第一个被测轧辊截面作为导轨误差的考察基准,则导轨在绝对坐标系内的误差数据为:

Δfc=fc-f0

(42)

Δgc=gc-g0

(43)

因为被测轧辊各截面测量坐标系原点Oc(c=1,2,3,…,C)所形成的空间曲线和导轨平行,所以导轨在UOW、VOW平面内的误差由(Δfc,Wc)和(Δgc,Wc)构成。其中Wc=cH/C+C1(C为测量的总截面数,C1为第一个测量截面的初始距离)。

2 建模与仿真验证

2.1 误差分离仿真步骤

步骤1:输入测点数N和q0、q1、q2确定三传感器的位置;输入预设被测轧辊截面c的轮廓傅里叶展开式;输入预设被测截面c在测量坐标系中回转误差x、y方向分量的傅里叶展开式;

步骤2:根据式(2)～式(4)计算传感器采集的数据;

步骤3:根据式(7)、式(8)计算出权值系数z1、z2,再把z1、z2带回式(6)计算出三传感器输出信号的加权和snc(i);

步骤4:对式(13)做离散傅里叶变换,得离散傅里叶的表达式snc(k),根据式(15)计算出分离权函数的各点值,把值带入式(14)并做离散傅里叶逆变换,可得被测截面c分离回转后的圆度误差vc(i);

步骤5:由式(17)～式(21)推导出等式右边都为已知序列的式(22)、式(23),带入已知序列vc(i+q1)、vc(i+q2)、s1c、s2c计算式(24)、式(25)的值;

步骤6:由式(26)～式(29)可计算出轧辊任意被测截面c离散傅里叶级数的一阶谐波分量正、余弦系数,结合式(31)、式(32)计算出最小二乘圆心(ac、bc);

步骤7:由式(33)被测各截面的回转误差λc,由式(34)、式(35)计算被测截面c的最小二乘圆半径差;

步骤8:由式(36)～式(39)推导出式(40)、式(41),由式(40)、式(41)计算出测量坐标系坐标原点(fc、gc)在绝对坐标系内的坐标;

步骤9:通过式(42)、式(43)得直行导轨在绝对坐标系内的误差数据;

步骤10:输出各图形和计算值。

2.2 各截面圆度误差分离仿真

预设被测轧辊截面c的轮廓傅里叶展开式为:

nc(α)=acsin(α)+bcsin(3α)+dcsin(4α)+
ecsin(6α)+fcsin(12α)

预设被测截面c在测量坐标系中回转误差x、y方向分量的傅里叶展开式为:

λxc(α)=axcsin(α)+bxcsin(2α)+dxcsin(4α)+
excsin(6α)+fxcsin(12α)

λyc(α)=aycsin(α)+bycsin(2α)+dycsin(8α)+eycsin(10α)

预设轧辊的半径为30 mm,轧辊长度为2 m,轧辊0.6 m处为第一个测量截面,每个测量截面之间间隔0.1 m,共仿真10个截面,即c=10,为使仿真结果尽可能接近实际测量情况,每个截面上的测量点数选取512,即N=512,q0、q1、q2为3个互质的奇数[10],分别取值为29、71、137。

3个传感器采集的数据如图2～图4所示。图2～图4显示了S1、S2、S3三个传感器分别对轧辊外廓进行数据采集的仿真图像,其中采集的数据包括预设的轧辊轮廓信息和回转轴的回转运动误差。为使仿真结果在图中易于观察,仿真过程中保持轧辊轮廓预设误差大小不变,各截面半径缩小100倍。

图2 传感器S1采集的待测轧辊轮廓信息 图3 传感器S2采集的待测轧辊轮廓信息

图4 传感器S3采集的待测轧辊轮廓信息

图5为经过三点误差分离之后的轧辊轮廓信息和预设的轧辊轮廓信息,图6是Z轴为0的投影,从图6投影后的预设轧辊轮廓和进行误差分离后的轮廓进行对比可以看出误差分离的效果很好。

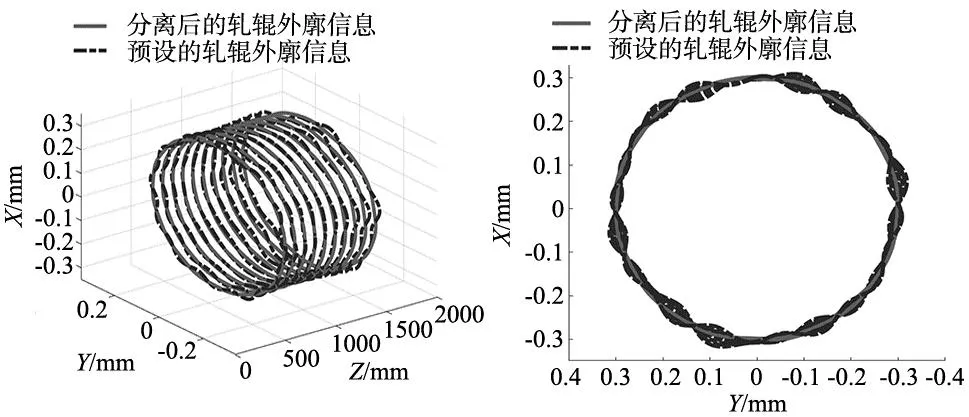
图5 分离前后轧辊轮廓信息 图6 Z轴为0的平面

2.3 各截面最小二乘圆心及半径差仿真

图7是分离出的回转误差,图8和图9显示了预设的最小二乘圆心位置和经过误差分离之后的最小二乘圆心的位置,使用传感器采集每个界面的数据时,传感器会采集回转轴产生的回转误差,通过把传感器采集的数据进行误差分离,结合图7～图9可知,经过误差分离之后,能很好地把3个传感器在X轴和Y轴方向产生的回转误差分离出来,得到不受回转轴运动误差影响的最小二乘中心位置。

图7 各截面回转误差 图8 最小二乘圆心在XZ方向的投影

图9 最小二乘圆心在YZ方向的投影 图10 各截面最小二乘圆半径

图10为各截面最小二乘圆半径,为便于看出各截面最小二乘圆半径的差值,把各截面最小二乘圆半径均缩小104倍,根据式(34)、式(35)计算出轧辊各截面半径差,差值如表1所示。设置不同的参数,仿真出多次对轧辊表面进行测量,共进行了3次仿真,其余两次图像结果展现出的分离效果和以上相同,此处不再赘述。

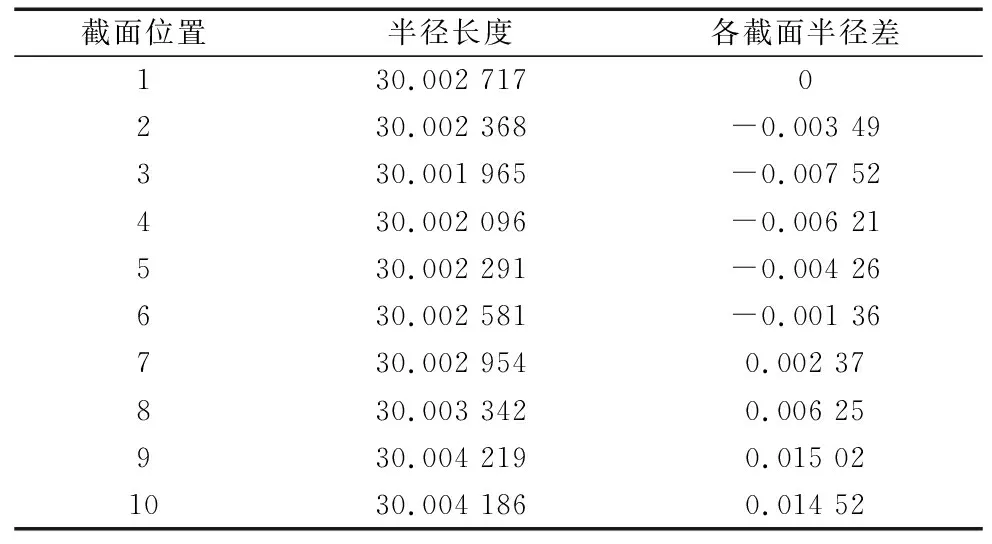
表1 各截面半径差值 (mm)

2.4 直行导轨误差仿真

图11和图12分别是轨道在绝对坐标系V轴和W轴上的移动误差,在实际测量中,对轧辊表面进行多次测量,能多次分离出导轨的移动误差,对分离出的导轨移动误差进行比较,若分离出的导轨误差在绝对坐标系中直线度误差和倾斜方向大致相同,则可认为分离出的导轨误差和导轨的实际形状是相同。通过设置不同的参数,对轧辊圆柱度误差分离仿真3次,得到3条直行导轨的移动误差,由图11和图12可知,3条直行导轨移动误差几乎重合,得出导轨的直行误差分离是正确的。

图11 V轴方向导轨误差 图12 W轴方向导轨误差

3 结束语

把三点误差分离应用到轧辊圆柱度测量,对组成轧辊圆柱度形状误差的3部分:各截面圆度误差、截面最小二乘圆心和截面半径差以及在测量过程中回转轴产生的回转误差和导轨的轨迹误差5个部分进行了数学推导。

根据所推导的公式,基于MATLAB平台,对预设的式子取不同的参数仿真3次,分离出轧辊圆柱度形状误差的基本要素:圆度误差、各截面半径差、最小二乘圆心,同时还成功分离出各截面的回转误差和导轨的轨迹误差。

圆度误差、各截面半径差、最小二乘圆心作为轧辊圆柱度形状误差的基本组成部分,这3部分还能重构出表征被测轧辊表面形貌,从而才能进一步按照一定的方法对轧辊圆柱度进行评定,分离出的回转误差和导轨轨迹误差能让评定出的圆柱度精度更高,为数控轧辊磨床3点圆柱度测量提供了理论支撑。