基于PSO-LSSVR的机器人磨抛材料去除模型*

蔡 鸣,朱 光,李 论,赵吉宾,王 奔

(1.沈阳航空航天大学机电工程学院,沈阳 110136;2.中国科学院沈阳自动化研究所,沈阳 110016;3.中国科学院机器人与智能制造创新研究院,沈阳 110169)

0 引言

随着科学技术的不断发展,愈来愈多新的技术被应用在航空制造领域,研究学者们也关注到了计算机技术在探究工艺参数与加工质量之间关系的独特优势。但相较于欧美等国,我国的航空制造技术研究起步较晚,现阶段仍有亟需解决的关键技术难题,其中航空发动机叶片的制造尤为重要[1]。航空发动机是飞机的动力来源,为了追求更高的工作效率和经济性,复杂曲面也更多的应用到航空发动机叶片的设计中,因此确保叶片制造的精度和加工效率十分重要[2]。

由于叶片的型面结构复杂,几何精度和表面完整性要求较高,是典型的难加工薄壁件。现阶段的叶片制造过程一般需要先精密铸造成型,再通过机械加工去除多余材料达到设计的几何精度。机械加工方法主要有:人工磨抛、数控机床加工、机器人砂带磨抛加工[3]。人工磨抛存在着加工效率低、表面一致性较差等问题;而数控机床加工精度较低,可能会产生加工刀痕,导致型面精度较差;机器人砂带磨抛加工具有柔性好,成本低,加工效率高等优势[4]。但砂带磨抛加工具有较高的柔性;加工过程中的叶片表面的材料去除深度受多种因素影响,需要建立明确的工艺参数与去除深度之间的关系,才能调节工艺参数控制材料去除深度。

对于砂带磨抛的材料去除深度控制的问题,国内外的研究人员已积累了一定的研究成果。WANG等[5]通过分析磨料颗粒和工件表面相互作用,计算参与切削的所有磨粒的去除体积,建立了一种线性工件表面材料去除深度预测模型,并设计实验验证该模型。ZHANG等[6]提出了一种基于神经网络算法的材料去除深度预测模型,主要考虑了接触力的大小对材料去除的影响,通过仿真工件的局部磨削过程,对模型的准确性进行验证;CHEN等[7]提出了一种基于灰色关联度的叶片材料去除率和表面粗糙度优化方法,将多目标优化问题简化为单目标优化,并利用RBF神经网络建立工艺参数与灰色关联度的映射关系,再利用FA算法获得最优的工艺参数;朱天宝等[8]基于Preston方程和Herts理论,提出了一种复杂曲面磨抛的材料去除模型,分析了材料去除量的影响因素及规律;张军锋等[9]基于Preston方程建立百叶轮柔性磨抛材料去除深度预测模型,确定材料去除深度的主要影响因素,并通过模拟仿真和实验验证了模型准确性。以上研究分别基于不同的回归方法建立有关材料去除的预测模型,此类方法可能会受到超参数设置的影响,且回归方法在不同的加工条件下的适应性不同,需要提出一种适应性更好的回归方法。

针对航空发动机叶片的砂带磨抛加工中材料去除策略难题,需要得到适应性好,准确性高的材料去除深度预测模型,本文建立了用于航空发动机叶片的高精度机器人砂带磨削系统,并根据多工艺参数实验数据提出一种基于最小二乘支持向量回归机(LSSVR)的叶片材料去除深度预测模型。为了保证LSSVR模型的性能,使用径向基函数(RBF)作为核函数,并使用粒子群优化算法(PSO)来优化超参数。因此,建立了PSO-LSSVR模型的混合模型以此达到预测目的。

1 叶片机器人砂带磨抛系统

根据叶片的机器人砂带磨抛加工要求,搭建了叶片机器人砂带自动磨抛系统,如图1所示。该系统以功能分类可有以下5部分组成:

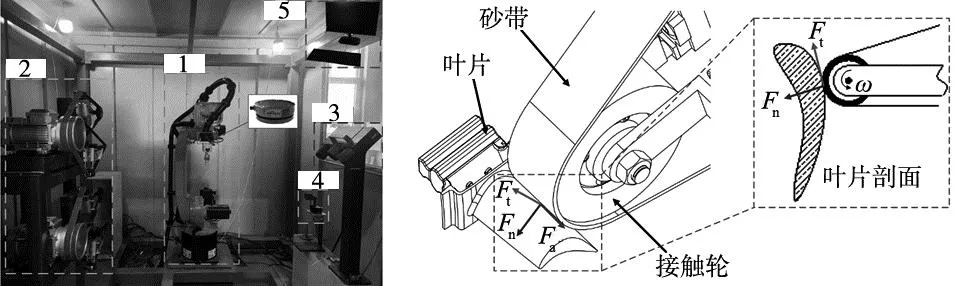
图1 叶片机器人砂带磨抛系统 图2 叶片磨抛接触区域示意图

(1)机器人装夹执行装置:由带有力传感器的某公司的六轴工业机器人KR-C4组成,机器人的重复定位精度小于0.06 mm,ati六维力传感器的Z向精度为1/16 N,固定在机器人末端执行器和用于保持工件的法兰之间;装置末端的夹爪有气缸控制,实现叶片的自动装夹。

(2)砂带机及张紧控制部分:通过电机的无极变速来达到砂带转速的控制,砂带机的张紧轮连接气缸,实现砂带的更换和砂带的张紧。

(3)非接触式测量系统:采用某公司的gom扫描仪对叶片进行三维建模,利用已开发的软件对叶片的实际三维模型与理论模型进行对比,可得到材料去除余量,还可以根据前后的去除余量计算出该次的去除深度。

(4)工件坐标系的标定系统:利用某公司的点激光位移传感器,基于六点定位原理对叶片的工件坐标系进行标定。

(5)系统控制部分:一台工控机实现机器人砂带磨抛系统各部分之间的通讯和数据检测。

对叶片表面与砂带接触区域进行分析,如图2所示进行受力分析。将接触力分为垂直接触切平面的法向接触力Fn、沿进给方向的磨抛切削力Ft、沿轨迹切线方向的滑动摩擦力Fa。磨抛过程中由六维力传感器采集接触力信号,再由工控机处理采用基于阻抗控制策略[10]实现对法向接触力Fn的恒定控制。

根据上述叶片机器人砂带磨抛系统进行叶片磨抛加工时,制定了磨抛加工的技术路线流程图如图3所示。首先机器人装夹执行机构自动夹取未加工叶片,并进行重力标定,再利用工件坐标系自动标定部分对叶片坐标系进行标定,然后由gom扫描仪扫描得到三维模型,经过工控机的数据处理可计算得到加工余量,并进行磨抛加工轨迹规划,设置磨抛工艺参数,机器人末端夹持叶片在砂带机上进行磨抛加工,最后对磨抛后的叶片进行质量评价,符合预期质量要求,则结束加工,不符合精度要求则返回继续磨抛加工。

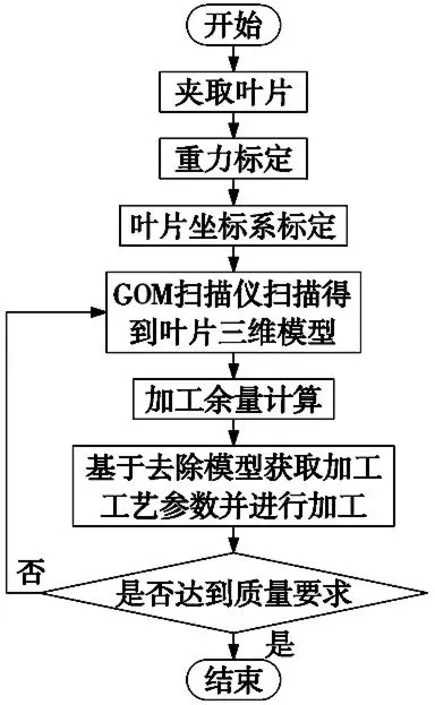
图3 机器人砂带磨抛系统加工技术路线流程图

2 PSO-LSSVR模型

支持向量机(SVM)是基于结构风险最小化的机器学习方法[11],SUYKENS等[12]提出了最小二乘法支持向量回归机(LSSVR),其是SVM衍生的一种可替代核算法,具有先进的完整理论体系,可以将二次优化问题的解转化为求解线性方程组,从而简化问题的求解。LSSVR可以更好地解决回归问题,而利用SVR解决回归问题时还需要考虑到超参数问题。本文为了获得上述加工技术路线中提到的去除模型,提出先基于LSSVR建立机器人砂带磨抛材料去除深度预测模型,再结合PSO对LSSVR中超参数进行选取的方法,即基于PSO-LSSVR的机器人砂带磨抛材料去除深度预测模型。该模型可有效提供工艺参数和去除深度的数学关系,且降低了模型存在局部最优的可能。

2.1 最小二乘法支持向量回归机(LSSVR)

在给定的训练集中含有N个点{xi,yi}N,xi为输入,yi为输出,对于非线性回归问题,期望获得以下形式的目标函数模型:

y(x)=wTφ(xi)+b+ei

(1)

式中:wT为权重向量,φ(xi)是将输入矩阵映射到更高维度特征空间的非线性映射,b为偏差项,ei表示第i个训练集的实际输出和预测输出之间的误差。

在约束条件为yi=wTφ(xi)+b+ei,i=1,2,…,N下,通过解决权重向量wT和偏差项b的最优化问题,表达式为:

(2)

式中:λ为正则化参数,影响模型的回归精度和复杂度。

利用拉格朗日乘子法对式(2)进行求解,得到拉格朗日函数为:

(3)

式中:αi为拉格朗日乘子。

优化条件:

(4)

转换为矩阵可得:

(5)

引入核函数K(xi,xj)=φ(xi)φ(xj),整理式(5)得:

(6)

式中:A为N维单位列矩阵,E为N维单位矩阵,Q=[φ(x1)Ty1;…;φ(xN)TyN],S=[y1;…;yN],e=[e1;…;eN],α=[α1;…;αN]。

求解式(6)得:

(7)

构造决策函数:

(8)

本文选择RBF高斯核函数,如式(9)其精度受参数δ的影响。

(9)

2.2 粒子群算法(PSO)

对于一个R维的空间内存在着n个粒子组成的粒子群H=[H1,H2,…,HR]T,其中第i个粒子Hi=[hi1,hi2,…,hiR]T表示粒子的空间位置,也是极值问题的一个潜在最优解。第i个粒子的速度Vi=[vi1,vi2,…,viR]T表示粒子的快慢程度,其个体极值为Pi=[pi1,pi2,…,piR]T,粒子群的全局极值为Pb=[Pb1,Pb2,…,PbR]T,粒子根据以下公式更新其位置和速度:

(10)

(11)

(12)

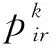
2.3 建立PSO-LSSVR模型

以上分别介绍了LSSVR及PSO,考虑到利用LSSVR建模时,模型的预测精度主要受正则化参数λ和核函数参数δ的影响,所以本文将PSO算法用于优化LSSVR模型的不定超参数,提高模型的预测精度,并降低产生局部最优解的可能。

寻求最小均方根误差(RMSE)作为优化目标,即计算PSO算法中的适应度函数Fitness,在本文中为预测值与实际测量值以得到随机粒子群中最优解,其公式为:

(13)

以PSO算法优化LSSVR模型的流程如图4所示,其步骤描述为:

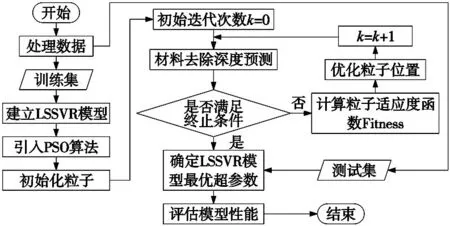
图4 PSO优化LSSVR流程图

步骤1:对数据进行归一化处理,并划分为训练集和测试集;

河道现状存在地表径流量持续减少，河床沙化、河道两侧植被覆盖率低、水土流失严重，个别河段河床被农业作物侵占等诸多问题，对河流生态造成极大影响。河头村生态蓄水工程作为桑干河河道综合治理的一部分，有增加水面面积和湿地面积、改善河道生态环境、提高河水自净能力，提升区域景观效果的重要作用。

步骤2:利用训练集建立初始LSSVR模型;

步骤3:基于粒子群优化算法,通过计算粒子适应度函数Fitness获取全局最优解;

步骤4:建立具有最优超参数的LSSVR模型;

步骤5:利用测试集对提出的PSO-LSSVR模型进行性能评估。

3 结果分析及验证

为了验证建立的PSO-LSSVR预测模型是否能准确地预测材料去除深度,在搭建的叶片机器人砂带磨抛实验平台上进行多工艺参数实验。本文主要考虑砂带粒度、砂带转速、进给速度、接触力和曲率半径5个影响因素,通过对比磨抛前后不同叶片截面上均与分布的各点材料去除深度,图5为叶片截面材料去除深度测量示意图,其中各点的曲率半径可在Solid Works软件中提取。

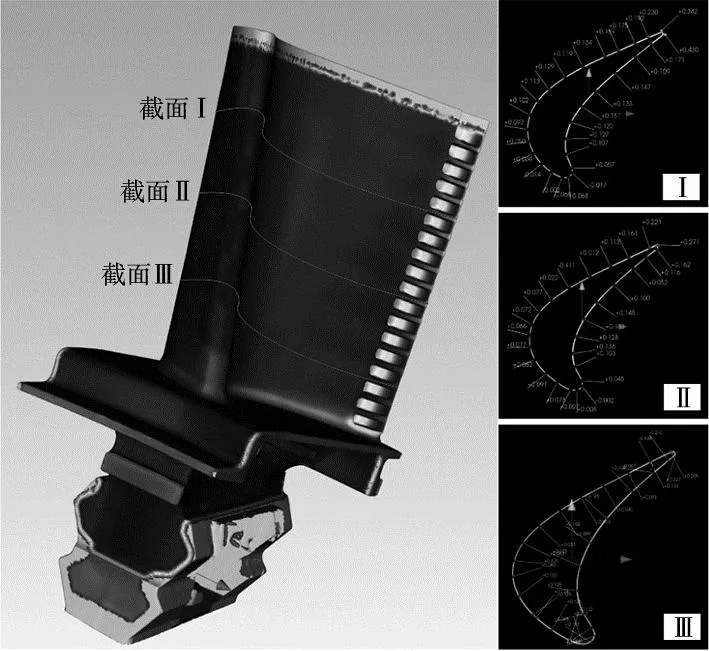
图5 叶片截面材料去除深度测量示意图

根据工程应用与实际加工情况,选用了目数为120、180、240、400的4种砂带,设置砂带转速为575 r/min、722 r/min、865 r/min、1004 r/min、1155 r/min,进给速度为3 mm/s、6 mm/s、9 mm/s、12 mm/s、15 mm/s,接触力为3 N、5 N、7 N、9 N、11 N,并以这些影响因素设计了26组参数实验,每组取3个截面,以截面上的一个点作为一个样本数据,一共得到1248个样本数据,部分实验数据如表1所示。

表1 部分样本数据

结合上文介绍的建立PSO-LSSVR预测模型流程,将实验数据随机排列后,以前1148个样本数据作为训练集用于建立模型,再利用后100个样本数据验证模型的可靠性。对于PSO算法中参数的设置:种群数目20、迭代次数100、加速度因子c1=1.5、加速度因子c2=1.7、惯性权重w=0.8,得到适应度迭代次数图如图6所示。

图6 适应度函数迭代过程

图7 PSO-LSSVR模型测试集预测结果对比 图8 测试集预测误差

为了进一步对上述得到的PSO-LSSVR模型的预测准确率和全局最优性进行分析,本文使用多元非线性回归(MNR)预测模型和SVR预测模型进行对比,分别计算平均绝对误差MAE、均方根误差RMSE、决定系数R2,表2为各模型预测精度对比。结果表明:相较于MNR、SVR模型,PSO-LSSVR模型的MAE和RMSE较小,说明其预测误差较小,可以更精确的进行材料去除深度预测,R2则反应模型拟合的相关性,可见模型的相关性排序为PSO-LSSVR>SVR>MNR。

表2 模型预测精度对比

为了验证预测模型在实际生产加工中的可行性,在叶片的叶背和叶盆上随机选取6个点,将各点的加工余量作为输入,并设定砂带目数为180、砂带转速575 r/min、进给速度9 mm/s,利用PSO-LSSVR预测模型输出目标接触力,结合上述工艺参数进行实验,对加工后的叶片进行检测,结果如表3所示。

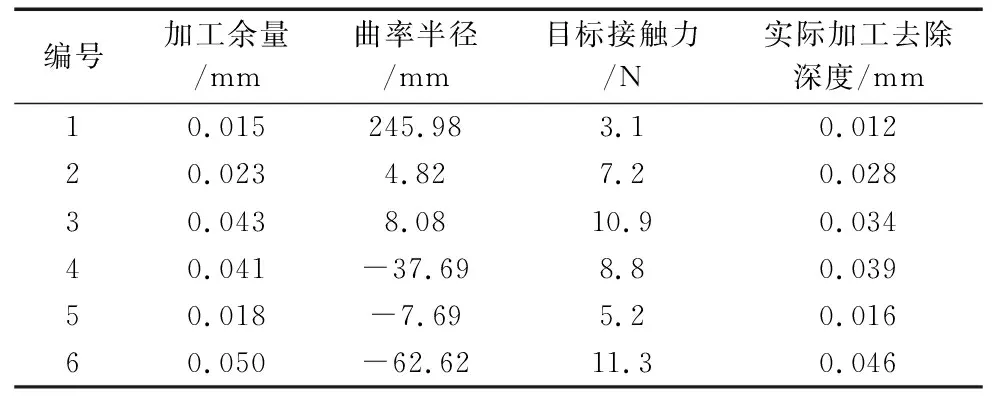
表3 实际加工验证数据

从表3中可以得到,在利用PSO-LSSVR模型输出的目标接触力进行加工后,平均加工误差在0.004 mm,与测试集结果近似,验证了PSO-LSSVR预测模型可有效的指导实际生产加工。

4 结论

(1)基于PSO-LSSVR建立的叶片机器人砂带磨抛材料去除深度预测模型,能够实现对叶片表面材料去除深度的预测,预测精度可达到95.37%,平均误差为0.003 463。

(2)通过对比PSO-LSSVR、SVR、MNR三种模型的预测精度,分别计算了各模型的平均绝对误差MAE、均方根误差RMSP、决定系数R2,可以发现PSO-LSSVR预测模型准确性更高,可以对材料去除深度进行有效且合理的预测。

(3)通过以加工余量作为PSO-LSSVR模型的输入,接触力作为输出,进行叶片机器人砂带磨抛实验,得到的平均加工误差为0.004 mm,进一步验证预测模型在实际加工的可行性。