旋转主轴轴系温升预测模型*

周学文,王彩年,毛范海,王 智

(1.大连理工大学机械工程学院,大连 116024;2.通用技术集团大连机床有限责任公司,大连 116620)

0 引言

主轴是许多机械产品的核心,从各类机床到大型风力发电机,汽车到精密模具等领域,无不扮演着关键的角色,其性能好坏、制造精度的高低直接影响了产品的质量。由于主轴轴系自身特点,长时间的运转会累积大量热,进而导致主轴受热膨胀产生变形,影响其精度[1]。因此,结合当下工业装备智能化、高效化、实时化趋势,对主轴轴系温升进行精确的预测与控制,是众多领域高端产品实现智能化的一大前提。

关于主轴轴系热特性的研究,最早始于上世纪中期,发展到现在随着温度传感设备的更新和仿真模拟技术的提升,主轴轴系热分析已迈入全新时代。陈小安等[2]建立球轴承热-机耦合模型,通过数值分析的方法分析轴系热态性能及其影响,并对主轴关键部位温升进行实验,认为电主轴前轴承负载处温升最高;HOLKUP等[3]提出基于滚动轴承主轴热力学模型的有限元分析方法,并高效精准计算出了主轴温度场分布和热变形;UHIMANN等[4]采用了有限元的方法,考虑了复杂的边界条件对电主轴建模,并结合实验数据,表明传热系数与瞬态热分析之间具有良好的相关性。张丽秀等[5]用实验数据获得了电主轴生热量,并将实验数据与仿真数据相结合优化了电主轴传热系数,建立了电主轴温度场预测模型。DAI等[6]同样通过实验数据与仿真结合的方式对变预紧电主轴建立了温度场预测模型,对传热系数采用的是梯度下降法,同时还对主轴热变形模型做出预测。

综合上述学者对于主轴热特性研究可知,主轴轴系内部热源的生热量以及各部件之间换热系数基本通过经验公式确定,无法对轴系温度场分布做到精确计算。本文通过建立主轴生热理论模型,在转速1400 r/min,轴向力2000 N,径向力1000 N的工况之下,计算生热量和传热系数理论值,然后建立该工况之下仿真模型,结合实验数据对生热量和传热系数进行优化,从而建立主轴轴系瞬态温度场预测模型,为主轴轴系智能化设计提供可靠的依据。

1 主轴轴系生热与传热分析

构成主轴轴系的零部件很多,由于这些零部件的结构、材料的差异,使得它们接合面之间的接触热阻和换热系数不同,进而构成了复杂多变的温度场。本文通过自行搭建的轴系结构如图1所示,其热源仅来自于轴承,实验环境位于厂房内,故外部热源忽略不计。

1.圆螺母1 2.法兰盘1 3.后端盖 4.预紧盘 5.轴承座 6.角接触球轴承 7.前端盖 8.法兰盘2 9.圆螺母2 10.主轴图1 主轴轴系装配图

1.1 主轴轴系生热量计算

依据所搭建轴系,其热源来自于轴承生热。轴承热量主要来自于滚动体与内外圈接触区的摩擦损耗和滚动阻力,所以可以通过计算轴承摩擦功耗计算其生热量大小。图2为主轴轴系受力模型图,D点为主轴端部受力点,承受外部的轴向力Fa和径向力Fr;B、C两点为轴承所在位置,为整个轴系提供支撑,受到来自主轴传递的力。

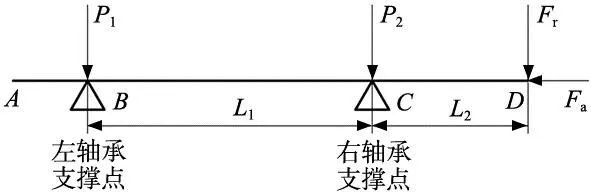
图2 主轴轴系受力图

根据PALMGREN[7]经验公式,轴承摩擦功耗主要由载荷引起的摩擦力矩M1和空载时润滑粘性引起的摩擦力矩M0两部分组成。

(1)由载荷引起的摩擦力矩M1计算公式为:

M1=f1P1dm

(1)

式中:f1是与轴承结构和载荷相关的系数,P1为决定轴承摩擦力矩的当量动载荷,N。

(2)由润滑引起的摩擦力矩M0计算公式为:

(2)

式中:f0是与设计和润滑有关的系数,v是润滑油动力粘度,mm2/s;n为轴承内圈公转转速,r/min。

引起轴承摩擦热的另一个重要原因就是球自旋产生的摩擦力矩,在前述基础之上引入内(外)圈沟道自旋摩擦力矩Msi(o),可使摩擦热计算更为精确:

(3)

式中:μi(o)为球与内(外)滚道接触摩擦系数,Qi(o)为球与内(外)滚道接触载荷,N;ai(o)为球与内(外)滚道接触处椭圆长半轴,mm;E(e)i(o)为球与内(外)圈接触处第二类椭圆积分。

轴承高速转动的过程之中,由于离心力的作用导致外圈接触角也会不同,因此需要将前述摩擦力矩等额分成内、外圈沟道分量,转化为接触区的局部分量,对于一个轴承不同方位角处的滚动体而言,其摩擦力矩计算为[8]:

(4)

式中:Mi(o)j为内(外)圈沟道第j个球的摩擦力矩,N·mm;Z为轴承滚子数,Dw为滚子直径,mm;di(o)为内(外)圈沟道直径。

综上所述,轴承在内外圈滚道产生的热量为[8]:

(5)

式中:ωroll为钢球相对于外圈滚道的角速度,rad/s;ωsi(o)为滚动体在内、外圈自旋角速度,rad/s。

1.2 轴系传热分析

对于轴承所在的主轴系统而言,其热量传递主要由热传导、热对流和热辐射组成。相较于轴承、主轴和轴承座之间的热传导,轴系中各零件之间温差较小,其热辐射占比很小,因此可以忽略其带来的影响[9]。

轴系中用一对角接触球轴承支承主轴,其热传递过程如图3所示,轴承热量的传播途径主要为两方面:①通过热传导将热量传递给轴系其他部位,包括:主轴外壳与轴承外圈之间的热传导、轴承外圈与润滑脂之间的热传导、润滑脂与轴承滚子之间的热传导、轴承滚子与轴承内圈之间的热传导、轴承内圈与主轴之间的热传导;②轴承表面与空气强迫对流换热;主轴和主轴外壳表面与外界环境之间的自然对流换热。

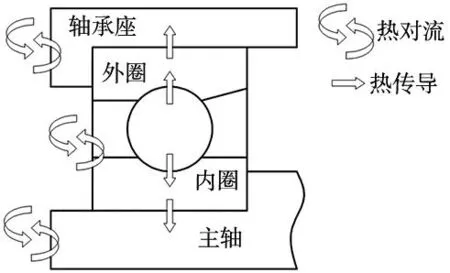
图3 热传递方式图

主轴轴承对流换热系数h计算通常按照HARRIS等[10]提出的经验公式得出:

(6)

式中:K为润滑剂导热系数,x为特征长度,Pr为普朗系数,Re为雷诺数。

空气自然对流换热系数经验公式为:

(7)

2 主轴轴系温升预测模型

由前述可知主轴热传递主要来自于热传导和热对流,由于热传导的传热速率主要与各零部件材料属性和各部位温差有关,故本文不从热传导角度提升温度预测精度。在已知轴承为一定热源的情况之下,考虑对其生热量和传热系数进行修正,进而建立出更精确主轴轴系温升模型。

2.1 生热量修正

由式(5)可知,对于轴系中确定的轴承,生热量主要与主轴所受载荷P、轴承润滑脂运动粘度v、主轴转速n等有关,且成比例关系。文献[11]给出主轴生热量通过测温点实时温度修正公式:

(8)

式中:H′为修正之后的生热量,W;Tf为有限元计算所得的测温点温度,℃;T∞为环境温度,℃;Tm为测温点实测温度,测温点选择轴系内轴承外表面,均布4组,分布如图4所示。

(a) 测温点分布实物图 (b) 测温点分布正视图图4 测温点分布图

2.2 传热系数修正

根据牛顿冷却定律,轴系温度和传热系数成反比,和热流密度成正比,其关系为:

q=h(T-T∞)

(9)

式中:q为热流密度,W/m2;h为表面换热系数,W/(m2·℃)。

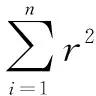
(10)

最终可得到各部分优化之后的换热系数值。

2.3 主轴轴系温度场预测模型

首先通过对轴系发热模型进行理论建模,计算出某工况之下的生热量和传热系数初始值,然后将这些初值加载到有限元模型之中,得到主轴轴系初始温度场;进行轴系实验,取得该工况之下采样点实时温度;提取实验温度数值和仿真温度数值,对生热量和传热系数优化,将优化之后的数值代入主轴轴系温度场有限元模型,得出精确的主轴轴系温度场。模型流程图如图5所示。

图5 主轴轴系温度场预测模型

3 温升实验

本文通过自行搭建轴系实验台来收集轴承温升数据,实验台实物如图6所示。实验台由主轴系统、加载系统、温度采集系统、电机动力系统等组成。

(a) 轴承实验台实物图 (b) 温度传感器布置图图6 主轴轴系温升实验台

实验台可以对被测轴承加载轴向力和径向力,主轴由电机驱动,内部仅有轴承单一生热源,而且结构简单、零件少,会提升测试温度的准确性。温度传感器PT100通过轴承端盖开孔插入轴承座中,与被测轴承外圈接触,末端相接数据采集系统。

温升实验条件为:主轴转速1400 r/min,轴向力2000 N,径向力1000 N;实验环境温度为9 ℃。实验前,先将温度传感器按照图4位置布置4个温度传感器,并进行调试。然后使用红外温枪记录环境温度;接着打开电机,调整转速,缓慢施加轴向力和径向力至指定工况;设置温度采样频率为每10 s采集一次,记录轴承外圈温升,直至其温度不再随时间升高,即达到热平衡状态。

该工况之下温升实验结果如图7所示,由图中结果可知,该工况之下前4000 s主轴轴系温升基本与时间成线性关系,之后温升趋势变缓。在8000 s左右时轴系达到热稳态,被测轴承外圈表面温度4号点位最高,达到18.5 ℃。

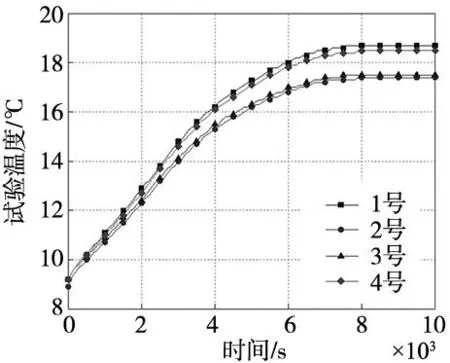
图7 温升实验结果

4 温度场模型仿真及其优化分析

本文针对自行搭建的主轴轴系进行热仿真。构建仿真模型时,在保证结果精度的基础之上忽略零部件倒角、螺纹孔等不必要特征;轴系内一对角接触球轴承是唯一生热源,其结构参数如表1所示。轴承内外圈采用扫掠划分网格,大小为2.5 mm;轴系其他零件采用六面体主导划分网格,根据设计尺寸,网格大小设置为6 mm,图8为主轴轴系网格划分图。由于在计算生热量时已考虑到摩擦力矩,所以轴承滚子和滚道接触面设置为绑定接触。

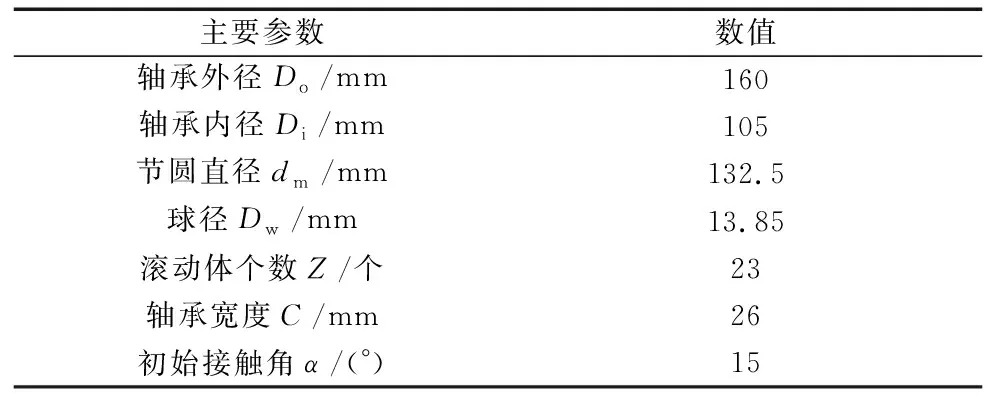
表1 7021C轴承主要结构参数

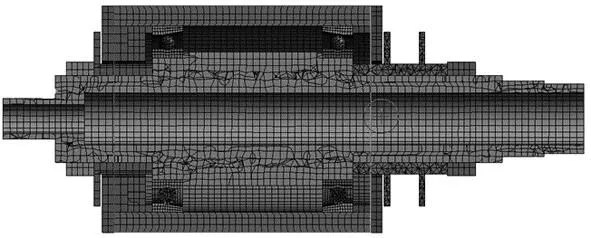
图8 主轴轴系网格划分图

表2给出了主轴轴系中各部件材料属性,除了主轴和轴承之外,其他部件材料都相同。

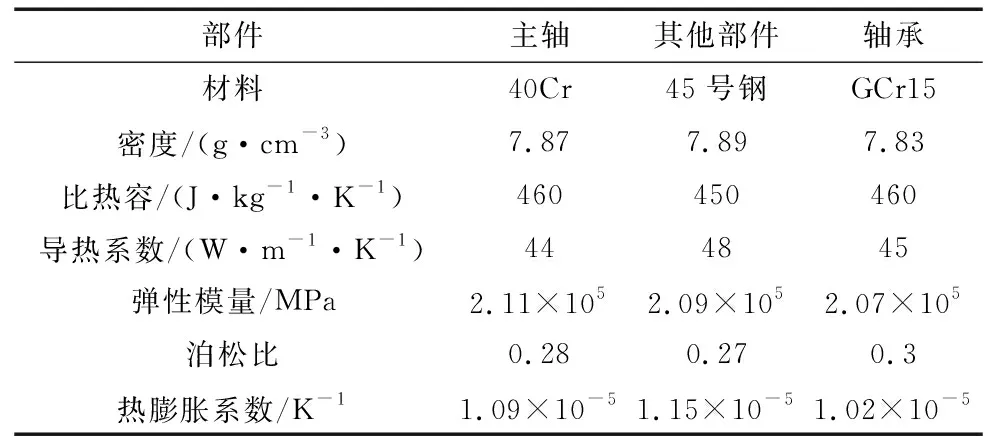
表2 各部件材料属性表

有限元分析边界条件设置为实验工况,将理论模型计算出的生热量和传热系数加载到有限元模型之中,计算出优化之前主轴轴系稳态温度场;然后以实验结果为对照,对生热量和传热系数进行优化,加载优化之后的结果得到优化之后的稳态温度场,优化前后的系数如表3所示。对比优化前后轴系温度场如图9所示,可以看出主轴轴系温度变化明显。图10对比看出轴承温度分布不均,这是由于轴系下部将一部分热量传递给支撑座,实验数据中1号和4号测点温度比2号和3号测温点略高也印证了这一点。

表3 优化前后边界条件

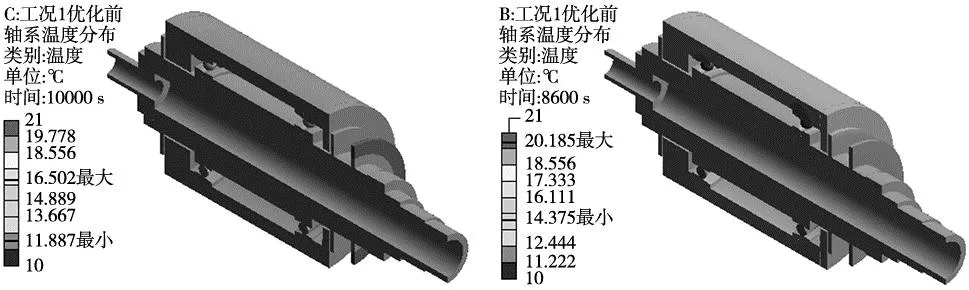
(a) 优化前主轴轴系温度场 (b) 优化后主轴轴系温度场图9 主轴轴系温度场分布云图

选取4号测温点实测数据,将优化前、优化后仿真数据和实验温度做对比,如图11所示。可以看出,在实验工况之下,主轴轴系在8000 s时达到稳态。优化之前主轴轴系温度预测模型平均绝对误差为2.74 ℃,相对误差为14%;优化之后轴系温度场预测模型平均绝对误差为0.89 ℃,相对误差为5%。优化后的温度预测曲线与实验温度曲线在轴系达到稳态后的有着较高的吻合度;达到稳态之前的温升阶段,平均相对误差达到7%,综合分析可能由于实验时间较长,实验场地环境温度变化造成的。

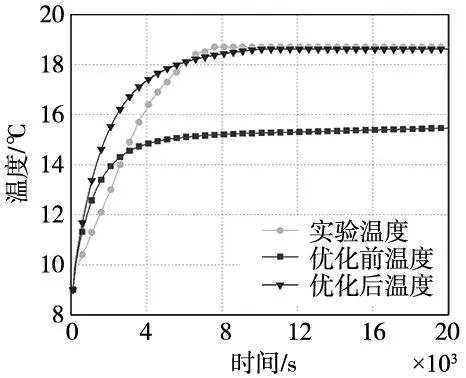
图11 4号测点优化前后实验温度与仿真温度对比图

5 结论

通过对主轴轴系温升预测模型的研究和实验对比分析得出以下结论:

(1)搭建的实验台仿真模型可以精确地模拟轴系温升分布情况,验证仿真模型的准确性。

(2)在对轴承生热量修正和传热系数优化的基础之上,建立了主轴轴系温度预测模型,优化后的预测模型平均误差降低了1.28 ℃,相对误差精度提高了9%,为主轴轴系温升的智能化控制提供了参考。