触发式测头在机标定方法研究*

李 禾,贺永海,袭萌萌,刘海波

(1.大连理工大学高性能精密制造全国重点实验室,大连 116024;2.西安航天动力机械有限公司,西安 710025)

0 引言

触发式在机测量系统的应用为工件的补偿加工及最终加工质量的检测提供了一种有效的检测方式[1]。与采用坐标测量机进行零件加工质量检测的离线测量方式相比,在机测量方式减少了工件转移与定位的时间,避免了二次装夹引起的定位误差,对保证加工质量、提高生产效率具有重要意义[2]。

触发式测头是触发式在机测量系统的重要组成部分,BARINI等[3]研究表明,对触发式测头进行有效标定可以大幅降低触发式测量系统的不确定度,提高在机检测精度。国内外学者对触发式测头的标定研究主要集中在测头预行程误差的标定。BUTLER[4]研究表明,预行程误差约占测量误差的60%,因此对测头预行程误差进行补偿具有重要意义。ESTLER等[5]根据机械电阻式测头的内部结构及受力情况建立了测头触发的力学模型,对预行程的变化进行了定量描述。JANKOWSKI等[6]运用赫兹接触理论,进一步建立了包含赫兹变形的预行程误差模型。LI等[7-8]通过分析测头内部运动支架的移动和测针的弯曲,提出了刚柔耦合的预行程误差模型。测头预行程误差存在各向异性,理论模型较为复杂,而且测头的各项参数与其理论值会有一定偏差,因此通过理论推导得到的预行程误差值会与其实际值之间存在偏差。高健、汤泽航等[9-10]先后提出基于径向基函数神经网络和基于最小二乘配置的预行程误差预测方法,通过测量标准球得到测头部分方向的预行程误差,以此为训练数据预测测头各个方向的预行程误差。但是基于数据驱动的建模方式在获取训练数据时并没有考虑机床空间误差对训练数据的影响,因此建立的预行程误差模型包含了机床空间误差的影响。NAFI等[11]利用多步误差分离技术实现了机床空间误差和测头预行程误差的分离,但是这种方法需要对标准球进行多次循环测量,耗时较长且只能获得近似解。高峰等[12]提出了一种基于误差隔离的触发式测头预行程误差标定方法,但是这种方法仅适用于金属测针,对于红宝石测头的测针并不适用。

触发式在机测量结果受机床空间误差和测头预行程误差共同影响,需要对两种误差分别标定与补偿。本文在分析金刚石车床空间误差的基础上,提出了虑及机床空间误差的预行程误差在机标定方法。同时根据测量系统测量及数据处理需求,提出了测头空间位置标定方法。实验结果表明,本文提出的方法满足测量系统的标定需求。

1 测头预行程误差标定方法

1.1 触发式测头工作原理及预行程

基于金刚石车床的触发式在机测量系统采用应变片式测头,其基本结构如图1所示。应变片式测头在机械电阻式测头的基础上加以改进,增加独立于运动机构的腹板并在腹板上加装应变片,通过应变片检测X、Y、Z三个方向的接触力并将它们的输出相加,以便任何方向的接触力超出触发力阈值时产生触发信号。

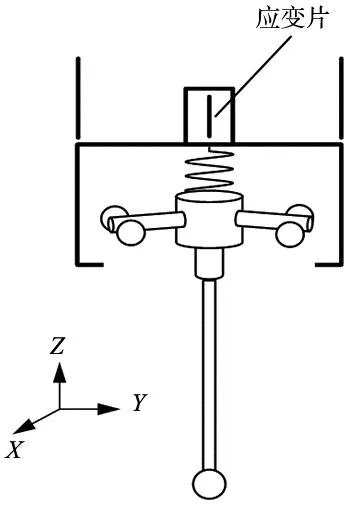
图1 应变片式测头基本结构

根据触发式测头的工作原理可知,测头在测针刚接触工件表面时并不会立即产生触发信号,只有当测针与工件之间的接触力超过测头的触发力阈值时,测头才会产生阶跃信号并发送至机床数控系统。数控系统捕捉到测头触发信号后记录当前机床坐标。触发式测头的工作原理导致机床控制器记录的机床坐标与测针刚接触工件表面时的机床坐标存在一段距离Δx,即预行程误差,如图2所示。

应变片式测头采用应变片检测X、Y、Z三个方向的接触力并将它们的输出相加,其预行程误差在X-Y平面内分布较为均匀,其大致形状如图3所示,但误差数值为未知量,需要对测头进行标定获得误差值。

1.2 金刚石车床空间误差建模

基于金刚石车床的触发式在机测量系统基本结构如图4所示。该系统选用应变片式测头,测头利用调整夹具水平安装至机床B轴工作台,通过调整B轴角度实现测针轴线与机床Z轴平行。在测量过程中,X轴带动主轴实现X向移动,Z轴带动测头实现Z向移动,主轴带动工件实现C分度转动。

图4 基于金刚石车床的触发式在机测量系统基本结构 图5 金刚石车床运动链

根据齐次坐标变换法可建立金刚石车床的空间误差模型,其拓扑结构为WCXFZT,如图5所示。

在理想情况下,测量坐标系t相对于工件坐标系w的齐次变换矩阵为:

wTt=wTccTxxTffTzzTt

(1)

在考虑几何误差情况下,测量坐标系t相对于工件坐标系w的齐次变换矩阵为(右上角标e表示该齐次变换矩阵受到误差的影响):

(2)

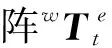
(3)

基于小误差假设,测量坐标系t相对于工件坐标系w的误差运动变换矩阵wEt可以假设如下:

(4)

式中:ηx、ηy、ηz为平移误差,γx、γy、γz为转角误差。

忽略二阶及二阶以上小量,由式(1)～式(4)可得金刚石车床空间误差模型如下:

(5)

1.3 虑及机床空间误差的预行程误差标定方法

触发式测头预行程误差的大小与触发速度、测针长度、测头触发角度等因素有关,其标定主要利用标准球完成,标定原理如图6所示。在标准球上预先规划n个测点,对应标定n个方向(θi,φi)的预行程误差err(θi,φi),i=1,2,…,n。根据预行程误差的定义,可以将预行程误差表示为:

图6 触发式测头预行程误差标定原理

(6)

式中:r为测球标称半径,R为标准球半径,(xi,yi,zi)为测球中心坐标,(x0,y0,z0)为标准球球心坐标。

(7)

2 测头空间位置标定方法

2.1 测头中心高度标定

基于金刚石车床的触发式在机测量系统在测量前需要将测针测球球心与机床主轴进行对中,该过程需要对测球球心偏离主轴轴线的高度进行标定。利用标准球和手动升降台完成测球中心高度的标定,标定模型如图7所示。将标准球找正、安装至机床主轴,利用升降台调整测针高度,使测球球心低于标准球球心,测量标准球的第1个截面圆,利用升降台将测针调高h,此时测针球心应高于标准球球心,测量标准球的第2个截面圆,两组测点坐标可分别拟合得到拟合圆半径R1、R2。由于两组测点数据为测量同一标准球获得,因此可认为两组测点分布在半径为R的球面上,根据几何关系可知:

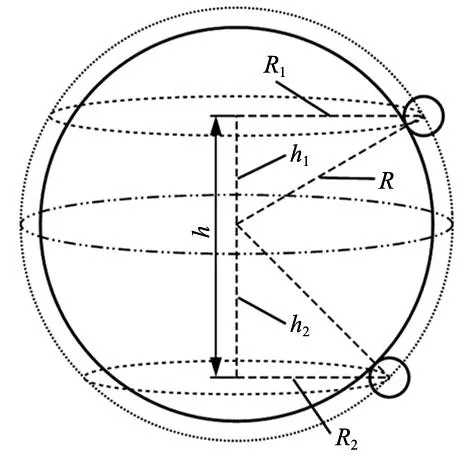
图7 测球中心高度标定模型

(8)

由式(8)可计算两截面圆在竖直方向偏离主轴轴线的距离,即两测量位置下测球中心偏离主轴轴线的距离h1、h2:

(9)

2.2 测头中心X向标定

金刚石车床的机床坐标系采用柱坐标系,工件坐标系采用笛卡尔坐标系,在处理测点数据需要将柱坐标系转换为笛卡尔坐标系,如图8所示。对任意测点A,测量系统获得的测点坐标为(x,z,c),根据式(10)可获得该点在工件坐标系下的坐标值(x′,y′,z′)。

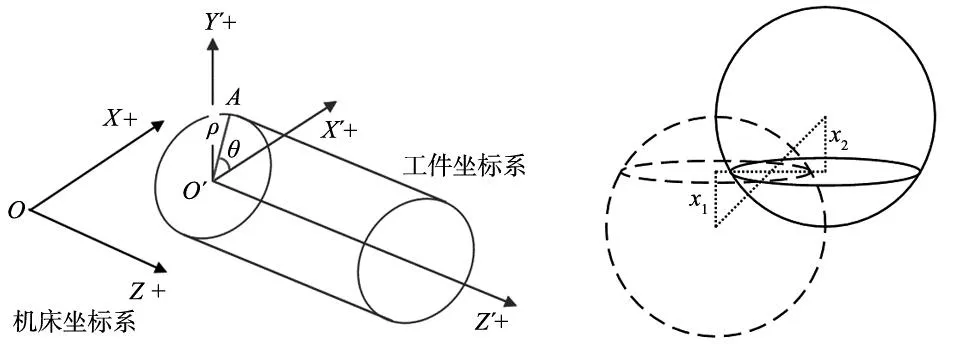
图8 机床坐标系与工件坐标系转换 图9 测头中心X向标定

(10)

由式(10)可知,在测点坐标转换前需要对工件坐标系原点位置xO′进行标定。通过测量标准球截面圆可拟合得到截面圆圆心坐标,圆心X坐标即为工件坐标系原点位置xO′。标准球在安装、找正过程中存在一定偏差,这导致在标准球调整安装后,标准球球心与机床轴线并不绝对重合,如果将截面圆圆心坐标直接作为坐标系原点坐标将对测量精度产生不良影响。为避免标准球安装偏心引入的误差,需要对标准球进行两次测量,两次测量C轴位置相差180°,如图9所示。将两次测量得到的圆心X坐标的平均值作为坐标系原点,即:

(11)

3 实验及结果分析

3.1 触发式测头在机标定

在对测头空间位置进行标定后,需要对测头预行程误差进行标定。在本测量系统中,触发式测头水平安装在机床B轴工作台,其工作角度为XOZ平面内0～180°范围,因此需要对该范围内的预行程误差进行标定。在利用激光干涉仪和球杆仪完成直线轴、旋转轴的几何误差标定后,利用标准球对测头预行程误差进行标定。将测量数据进行机床空间误差补偿后由式(6)得到触发式测头工作范围内预行程误差。触发式测头如图10a所示,标定结果如图10b所示。根据标定结果可知,应变片式测头的预行程误差具有较好的一致性。

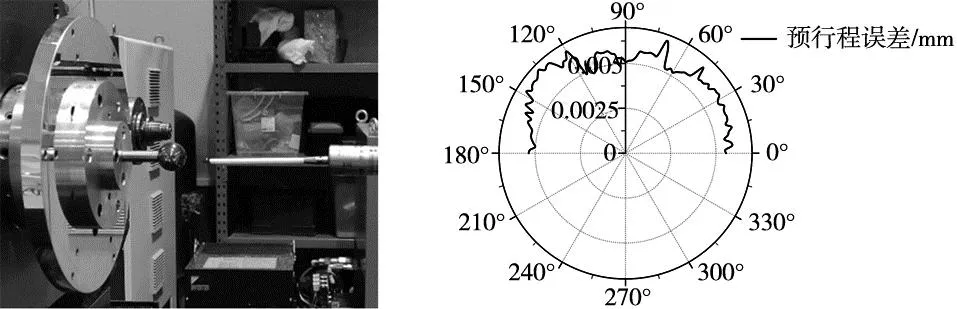
(a) 测头标定 (b) 测头0～180°范围内预行程误差标定结果图10 测头预行程误差标定

3.2 触发式在机测量系统测量精度测试

在对测头空间位置及测头预行程误差进行标定后,利用触发式在机测量系统检测典型特征型面,并将在机检测结果与三坐标测量机检测结果进行比较,以验证标定方法的有效性和在机测量系统的测量精度。

选取平面、柱面与球面作为典型特征型面,在利用金刚石车床完成上述型面加工后,利用触发式在机测量系统测量端面平面度、圆柱面直径与球面母线轮廓度,在机测量过程如图11所示。完成在机测量后,利用三坐标测量机对上述测量指标进行离线测量。离线测量采用与在机测量相同的测点分布方式,待测指标均采用最小二乘法进行评价,在机测量与离线测量的测量结果如表1所示。根据测量结果可知,本文提出的测头标定方法对基于金刚石车床的触发式测头进行了有效标定,保证了在机测量系统的测量精度。

表1 离线测量与在机测量结果 (mm)

(a) 平面度测量 (b) 圆柱直径测量(c) 球面母线轮廓度测量图11 典型样件特征在机测量

4 结论

(1)在分析金刚石车床空间误差的基础上提出了虑及机床空间误差的触发式测头预行程误差标定方法。

(2)根据基于金刚石车床的触发式在机测量系统标定需求,提出了测头空间位置标定方法。

(3)对触发式测头进行在机标定,分别利用触发式在机测量系统与三坐标测量机对典型型面特征进行测量,在机测量结果与三坐标测量结果偏差均小于2 μm,测量结果验证了本文提出的标定方法的有效性。