基于改进的SURF算法的机械臂识别定位及抓取研究*

李鑫炎,周 敏,张美洲,陈燕军

(武汉科技大学 a.冶金装备及其控制教育部重点实验室;b.机械传动与制造工程湖北省重点实验室;c.精密制造研究院,武汉 430081)

0 引言

当前机械臂广泛应用于各种领域,为多种工作减轻劳动强度并大幅度提高工作效率。现今一部分适配双目立体视觉[1]的机械臂多以特征点检测、匹配及三维重建[2]作为对目标识别定位的关键技术。在特征点的检测匹配算法中,SURF(speeded-up robust feature)[3]是对SIFT(scale-invariant feature-transform)[4]的一种改进,能在保留图像尺度及旋转不变性的同时处理速度更快,效率更高。但传统SURF算法会产生较多误匹配点对且会生成64维描述子,不仅匹配准确度低,运行中的计算、匹配速度也较慢,无法满足现场作业的实时性要求。黄春凤等[5]基于改进的RANSAC算法剔除错误匹配对,弥补了传统SURF算法存在的匹配精度低的缺陷,但该算法生成的高维特征描述符会导致运行速度偏慢。陈伟等[6]利用FAST角点取代SURF斑点在图像重合区域提取特征点,解决了传统SURF算法计算时间长问题,但利用FAST角点提取特征点时存在检测特征点重复、不是最优点等缺陷。张文卿等[7]基于Radon变换对SURF描述符降维,有效提高了彩色图像的配准速度及配准精度,但该算法在去除误匹配点时仍存在需要特征点对较多、剔除误匹配效果不佳等问题。

针对上述算法存在的问题,本文提出一种改进的SURF算法,在传统SURF算法的基础上通过基于rBRIEF的特征描述和基于低方差过滤的特征降维以降低特征描述符的维度,提高运行速度;引进基于Hamming距离的2-NN特征点交叉匹配与基于RANSAC算法的误匹配剔除以减少重复特征点对的产生,提高误匹配剔除效果。最后在自主搭建的实验系统中应用该算法,实现机械臂对目标的识别定位及实时自动抓取。实证分析表明,采用该算法能在保证较高匹配准确度的前提下,使匹配速度较传统SURF算法大幅度提高,并有效提升机械臂抓取的实时性及精准性。

1 机械臂识别定位及抓取实验系统搭建

搭建的机械臂识别定位及抓取实验系统主要由四自由度机械臂、计算机、双目相机、目标等组成,其中双目相机采用“Eye-to-hand”的手眼标定方式与计算机及机械臂连接,如图1所示。

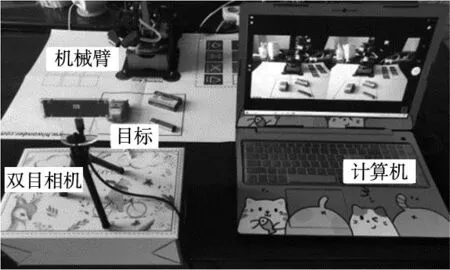
图1 机械臂识别定位及抓取实验系统

根据实验系统中各模块不同的功能特点,将机械臂识别定位及抓取实验系统分为识别定位子系统、控制子系统与抓取子系统。在识别定位子系统中,首先采用改进的SURF算法对目标物体经过预处理后的数字图像进行特征匹配并筛选错误特征匹配对,随后利用双目相机的三维重建技术求得目标的空间三维坐标信息,完成对目标的实时定位。控制子系统主要由Jetson Nano控制系统进行控制。抓取子系统的功能则主要依靠HTS-35H舵机实现,将机械臂逆运动学求解获得的各关节驱动角信息传输到机械臂Jetson Nano控制系统,再通过Jetson Nano控制HTS-35H舵机带动末端执行器完成对目标的抓取作业。3个子系统通过Visual Studio与MATLAB两种环境实现配合运作,机械臂识别定位及抓取实验系统框架如图2所示。

2 改进的SURF算法

SURF算法构建的尺度空间能够提取带有尺度的特征点[8],rBRIEF描述子可以生成便于特征高速匹配的二进制编码特征描述子,且较传统BRIEF描述子还具备了旋转不变性的特性,因此传统SURF算法搭配rBRIEF描述子可以实现图像特征的高速匹配及准确识别。改进的SURF算法具体流程为:利用传统SURF算法提取出目标图像特征点,确定所取特征点的主方向,再采用rBRIEF描述子与低方差过滤分别对提取特征实施描述及降维。降维后,每个特征点只保留32维的描述子。通过进行基于Hamming距离的2-NN特征点交叉匹配以筛除误匹配点对,随后配合RANSAC算法对图像中仍存在的误匹配点对进一步剔除。最后,输出目标的特征匹配图像,传统SURF算法及改进后的SURF算法流程对比如图3所示。

2.1 特征点提取及定位

传统SURF算法的基本流程主要包括4个部分:尺度空间建立、特征点定位、特征点主方向确定,特征点描述。由于构建尺度空间需要构造Hessian矩阵,故需要先对目标图像进行高斯滤波处理为构造Hessian矩阵做准备,经过滤波后尺度为σ的点(x,y)处的Hessian矩阵表述如式(1)所示。

(1)

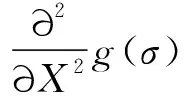
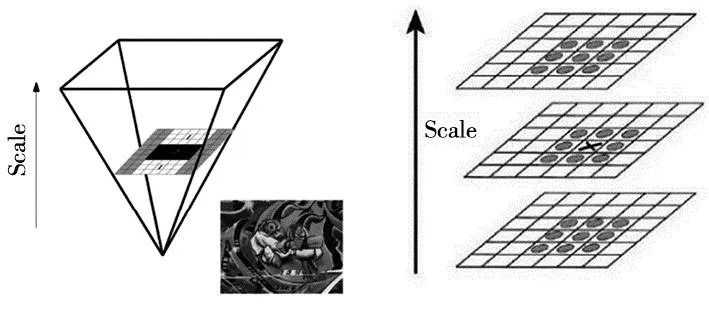
图4 构建尺度空间 图5 精确定位特征点

2.2 特征点主方向确定

传统SURF算法采用计算特征点圆形领域内的Harr小波特征作为确定特征点主方向的方法,即在特征点的圆形邻域内,以60°扇形为一个区间,计算区间内所有点的水平、垂直Harr小波特征的总和并形成矢量,随后扇形以0.2 rad的间隔重复旋转并进行统计,最终将扇形方向中最长的矢量作为该特征点的主方向。通过反复进行上述步骤即可得到所有已提取特征点的主方向,特征点主方向确定过程如图6所示。

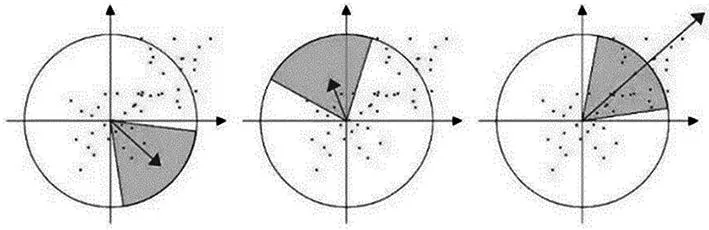
图6 确定特征点主方向过程

2.3 rBRIEF特征描述

rBRIEF(rotation-aware BRIEF)特征描述子[9]是一种二进制编码描述子,能够在事先取得特征点位置的情况下建立特征描述符,可以大幅度加快描述子的建立速度与特征的匹配速度。rBRIEF特征描述流程分为3步:首先,对目标图像进行高斯滤波处理以减少噪声的干扰;其次,以特征点为中心取一定半径的圆形邻域窗口,在此圆形窗口内以特征点和窗口质心的连线为x轴建立二维坐标系并随机选取一对点,通过比较像素点的灰度值大小进行二进制赋值,如式(2)所示。

(2)

最后,在窗口中随机选取K对点(K一般取256),重复上一步中的二进制赋值过程以形成一个二进制编码,如式(3)所示,此编码即是对特征点进行描述的特征描述子。

fk(p)=∑1≤i≤k2i-1τ(p,xi,yi)

(3)

式中:τ表示二值测试函数,p(x)、p(y)分别表示随机点x、y的像素值,i表示1～256区间的数字变量。

2.4 特征降维

图像中提取的每一个特征点经过rBRIEF描述子进行特征描述均会得到一个256位二进制描述符,因此改进后的SURF算法将生成64维特征描述子。其中检测到的无用特征点及生成的高维描述子均会提高运算复杂度,在进行匹配过程中还将降低匹配速度并产生误匹配点对。因此本文对高维描述子采用低方差过滤的特征降维方法,以达到缩短特征匹配时间的效果,具体流程如图7所示。

图7 特征降维流程

步骤1:将256位二进制描述符分为4个样本矩阵,每个矩阵包含64个样本数据且都为8×8标准矩阵;

步骤2:计算样本矩阵每一列均值,由于每个二进制描述符数据为0或1,故将均值设置为0.5,均值越接近0.5则说明该列方差越大,代表特征样本值有较多差别,而均值越偏离0.5则说明该列方差越小,代表特征样本值有较多重复,据此对列方差大小进行比较,将方差最小列从矩阵中剔除;

步骤3:对4个样本矩阵重复上述步骤,剔除所有方差较小的数据样本列并重新进行整合,最终得到128位二进制描述符(32维特征描述子),达到降维目的。

2.5 特征匹配

经过降维处理后,首先对128位二进制描述符间进行Hamming距离D的计算,随后根据Hamming距离设置相应的误差阈值ε,对待匹配的两特征点进行相似度比较以筛除错误特征点并将正确匹配对保留,误差阈值ε可根据文献或实验获得。当D<ε时,则代表特征点属于同一组,可认为匹配结果正确。当D>ε时,代表特征点不属于同一组,可认为匹配结果错误。虽然通过Hamming距离匹配已筛除掉大部分的错误匹配,但仍有少量的错误匹配存在。针对此问题,本文依据K最邻近(K-nearest neighbor,KNN)算法[10]能筛除不属于同一区域匹配点对的功能,对特征点的特征描述向量进行基于Hamming距离的2-NN交叉匹配[11]。

基于Hamming距离的2-NN交叉匹配通过找到待匹配点的最邻近点pi与次邻近点pi+1,并设置最邻近点Hamming距离Di与次邻近点Hamming距离Di+1的比值δ(如式4所示)来判断最邻近点是否属于同一区域,也避免了因阈值ε太相似而导致的错配现象。

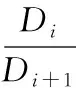
(4)

2.6 误匹配剔除

筛除非同一区域的匹配点对后,本文采用随机抽样一致(RANSAC)算法[12]对仍存在的误匹配点对进行剔除,RANSAC算法基本步骤为:首先选择最小数据点集拟合出最优的数据模型,并使用数据集来计算出当前数据模型,随后将所有数据点带入得到的当前数据模型中计算误差,统计出所有满足误差阈值的点数目(“内点”),最后比较当前数据模型与之前最优的数据模型间内点的数量,保留最大“内点”数据模型的参数及其“内点”数目。重复上述步骤,直到内点数目超过一定数量则表示迭代结束,当前数据模型已达到最好。

3 双目立体视觉三维重建原理与目标定位

双目立体视觉能模拟人眼获得场景中的深度信息,因此可利用两台相机从不同位置同时采集被测目标的数字图像对并建立图像特征间的对应关系,随后基于视差原理,通过计算图像对应点间的位置偏差以获取目标的空间三维位置信息,双目立体视觉三维重建原理如图8所示。

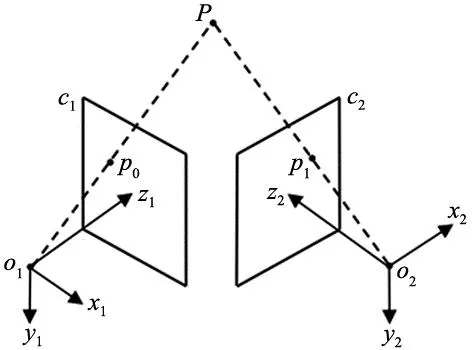
图8 双目立体视觉三维重建图

已知空间某点P的世界坐标(xw,yw,zw)T与该点对应的投影点像素坐标(u,v,1)T间的关系有:

(5)

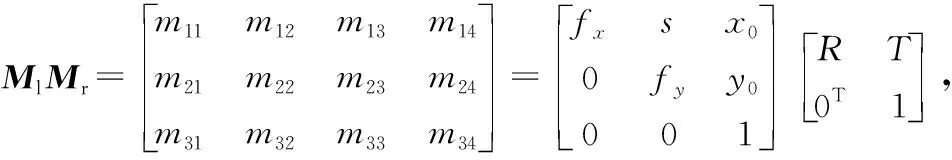
由于Ml、Mr为两相机的投影矩阵,z分别为zc1、zc2,故对于两相机分别有:

(6)

(7)

另外,目标图像与模板图像的图像像素坐标(u1,v1,1)、(u2,v2,1)及图像物理坐标(xl,yl)、(xr,yr)的转换如式(8)所示。

(8)

将式(7)中zc1及zc2消除并整理写为矩阵形式可得:

(9)

即:

AP=b

(10)

式中:

由最小二乘法可以得到[13],目标的空间三维坐标为:

P=(ATA)-1ATb

(11)

4 实验方案、验证及结果对比分析

4.1 实验方案设计

本文首先采用SIFT、传统SURF及本文改进的SURF算法对目标进行识别及特征点匹配准确度对比实验以验证改进的SURF算法的有效性和准确性,随后开展双目立体视觉定位实验以获取目标的空间三维坐标信息,最终通过编写逆运动学求解程序获得机械臂的各关节驱动角并完成机械臂抓取实验。本次实验的硬件工具为HBV-1780高清双目相机、HiWonder Jetson Nano机械臂,实验软件工具包括Microsoft Visual Studio 2012、PyCharm2021中的python3.9、opencv-python4.6.0.66以及MATLAB2018b,实验环境为Inter(R)Core(TM)i5-8300h CPU@2.3 GHz,16 GB内存,Windows 10计算机系统,抓取实验目标为蓝牙耳机充电盒。

4.2 实验验证与结果对比分析

4.2.1 目标识别及特征点匹配准确度对比实验

机械臂在实施抓取过程中,目标的位姿可能会因现场情况而发生旋转、平移等变化,因此在对目标图像与模板图像采用改进的SURF算法进行匹配时,需分别记录目标在旋转、平移变化下的识别匹配情况,以此完成在目标位姿变化下的算法效果检验,如图9所示。

(a) 旋转情况

另外,改进的SURF算法的识别匹配性能也会受光照强度、遮挡及较大图像尺度变化的影响,故还需分别检验在上述变化下的算法效果,以进一步验证本文算法的有效性,如图10～图12所示。

图10 不同光照强度的算法识别匹配效果

图11 受遮挡的算法识别匹配效果

图12 图像尺度变化的算法识别匹配效果

确定改进的SURF算法在上述因素影响下整体性能仍较好后,分别采用3种算法提取图像中的特征点并进行匹配,得到的各算法运行结果如表1所示,图13为验证不同算法所进行的目标特征点识别及匹配实验。

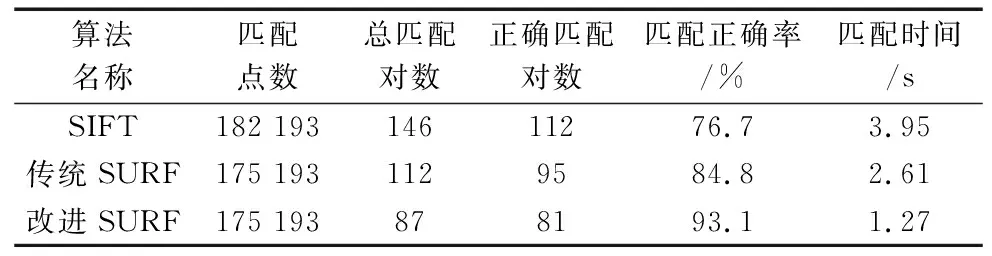
表1 各算法运行结果

(a) SIFT算法特征匹配实验

分析上述实验结果(见表1)可知,由于传统SURF算法与改进的SURF算法所采用的特征点检测方法相同,故最终目标图像与模板图像上的特征点数均相等。在匹配点数上,SIFT、传统SURF较改进的SURF算法更多。但在正确匹配对数方面,改进的SURF算法点对匹配正确率达到了93.1%,显然高于SIFT、传统SURF算法。另外,改进的SURF算法经过误匹配剔除后,较传统SURF算法减少了点对的总匹配对数,使特征匹配时间较SIFT算法缩短67%,相比传统SURF算法缩短51%。综上所述,改进的SURF算法可在保证较高匹配正确率的前提下提高机械臂对目标的识别速度。

4.2.2 双目立体视觉定位实验

为了取得目标的准确坐标,需要在特征匹配后开展双目立体视觉定位实验。定位实验主要是根据投影点像素坐标和相机主点坐标分别通过式(8)和式(11)计算出目标、模板图像的物理坐标及目标的空间三维坐标。目标的实际测量坐标主要通过MATLAB2018b进行双目相机标定并基于PyCharm2021编程显示其对应空间三维坐标获得。经过多次实验后,取实验中前四组定位结果,如表2所示。由表2可知,视觉定位的目标空间三维坐标与目标的实际测量坐标之间的平均误差为(0.14,-0.30,1)(mm),定位平均误差在机械臂识别误差范围内,据此验证了本文双目立体视觉三维重建对目标的精确定位效果。

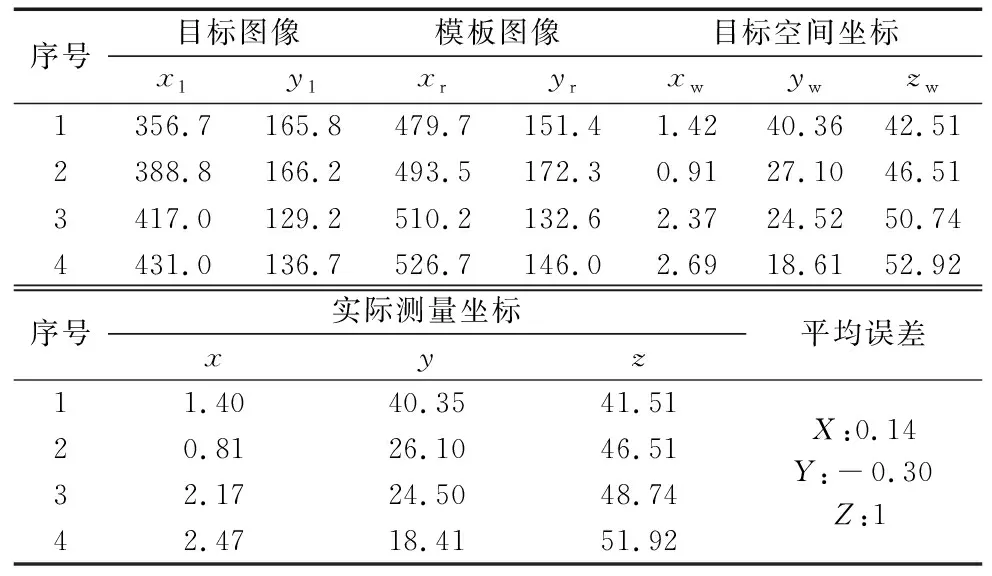
表2 目标空间三维坐标定位结果 (mm)

4.2.3 机械臂抓取实验

在进行抓取实验前需先调整好机械臂的初始状态,同时将目标放置在双目相机视觉范围内。求得目标的三维坐标后,通过MATLAB机器人工具箱编写逆运动学求解程序以获得机械臂的各个关节驱动角,随后将驱动角信息传输至机械臂Jetson Nano控制系统,由控制系统驱使HTS-35H舵机带动机械臂各关节运动并执行抓取动作,完成抓取后各项坐标信息将实时反馈回计算机系统,抓取过程如图14所示。

(a) 步骤1 (b) 步骤2

机械臂完成自主抓取时到达的实际位置与双目立体视觉定位坐标位置之间产生的平均位置误差为(1.18,0.52,0.63)(mm),如表3所示。由于目标的长、宽、高分别为:58 mm、45 mm、20 mm,且实验误差在机械臂允许的抓取误差范围内,因此验证了本文改进的SURF算法与双目立体视觉三维重建相结合能够实现机械臂的精确抓取。

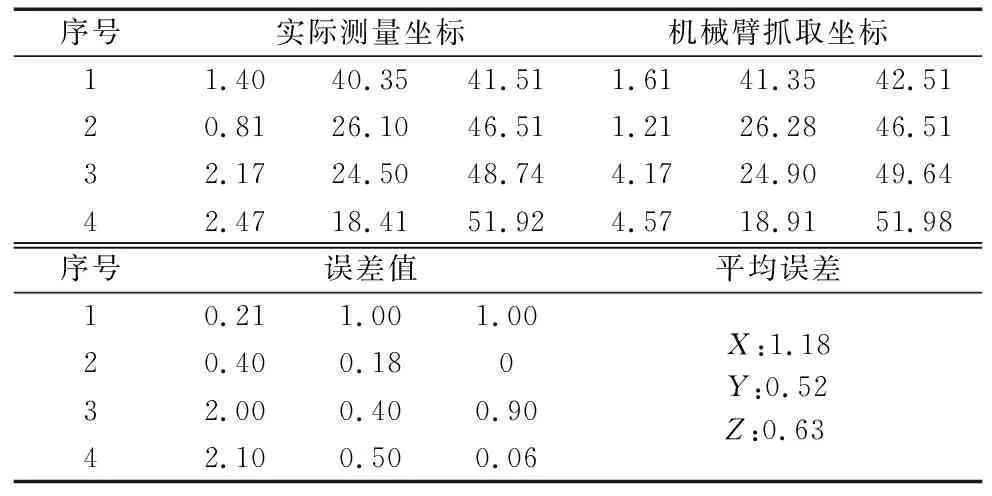
表3 机械臂抓取误差数据 (mm)

5 结论

本文通过改进的SURF算法结合双目立体视觉三维重建对机械臂的识别定位及抓取实验系统进行了深入研究,最终引导机械臂对目标实施实时抓取。实验结果表明:本文所提出的改进的SURF算法识别正确率可达到93.1%,整体匹配时间较传统SURF算法缩短51%,能在保证较高匹配准确度的前提下,使匹配速度较传统SURF算法大幅度提升,对机械臂工作区域内目标的快速、准确识别以及机械臂的实时、精确抓取具有较高的实际意义与应用价值。