基于UMAP改进的多域特征提取方法及轴承故障诊断*

尹泽明,王彩年,王 智,毛范海

(1.大连理工大学机械工程学院,大连 116024;2.通用技术集团大连机床有限责任公司,大连 116620)

0 引言

滚动轴承在机械设备中是应用最多也最易损坏的零件。据不完全统计,由滚动轴承引起的故障约占旋转机械故障总数的30%[1],因此准确且迅速地判断滚动轴承的运行状态并采取应对措施非常重要。由于受到负载、碰撞和环境等因素的影响,传统的特征提取技术很难在振动信号中找出具有代表性的特征信息,增加了诊断的难度。

针对这个问题,研究人员分别在信号的时域、频域与时频域上提取特征信息尝试提高故障诊断的准确率[2-4]。但是单一域的特征提取往往会忽略掉振动信号中的重要信息造成部分误判,彭宅铭等[5]通过多域特征提取提高滚动轴承故障诊断的准确率。

虽然多域特征集对故障的表征会更全面,但是其维度过高、信息冗余和非线性等问题会降低识别度准确率。

郑新[6]采用了EMD与PCA结合的滚动轴承故障诊断方法对相关矩阵进行降维,有着较高的准确率。JIANG等[7]将变尺度离散熵和t-SNE结合,对混合尺度模型进行降维,能够有效的识别故障类型。但PCA的主成分特征维度的含义具有模糊性且会丢掉很多底层的结构信息,t-SNE可以保留底层的数据结构但是计算速度非常慢,而统一流行逼近与投影算法(uniform manifold approximation and projection for dimension reduction,UMAP)[8]既可以获得PCA的速度优势又能保留更多特征集中的数据信息。

因此为提高多域特征提取方法对故障类型识别的准确率、降低计算资源占用、加快识别速度,本文提出了基于统一流形逼近与投影算法(UMAP)改进的多域特征提取方法。通过此方法建立的特征集输入到支持向量机进行诊断模型的训练,采用某大学滚动轴承实验信号将基于UMAP算法改进的多域特征提取方法与不同算法改进的多域特征提取方法进行对比分析,进一步验证该方法在滚动轴承故障诊断中的可行性。

1 改进的多域特征提取方法

1.1 多域特征提取方法

为保留更多特征信息本文选取了多种时域、频域特征参数构成时域特征向量S、频域特征向量P,具体如表1所示。

表1 特征参数分类

滚动轴承一但发生故障会导致振动信号的某些频段的能量发生一定的变化,能量矩[9]是将经CEEMDAN分解[10]产生的IMF分量做对时间轴的积分而得到的能量,表达式为:

(1)

式中:Δt为采样周期,n为总采样点数,k为采样点,Ci(t)为轴承振动信号CEEMDAN分解产生的IMF分量。

将其归一化并构造能量矩特征向量L为:

L=[E1,E2,E3,…,EN]/∑iEi

(2)

样本熵算法对近似熵算法进行了改进,同时相比小波能量熵更抗干扰。样本熵越高,信号的时间序列越混乱。对给定容限r的m维向量其样本熵的表达式为:

(3)

当L为有限值时,样本熵的近似值为:

(4)

式中:m为维数取值一般为1或2,相似容限r的取值范围一般为原始数据标准差的10%～25%。本文选取m=2,r为20%。

构造样本熵特征向量SE:

SE=[SampEn1,SampEn2,…,SampEnN]

(5)

由于不同故障类型的信号经过CEEMDAN分解后会产生数量不等的IMF分量。因此为保证各组数据多域特征集的特征与维度一致性,采用相关系数法计算选取与原始振动信号互相关系数ρi(τ)≥0.1的IMF分量提取能量矩与样本熵特征。

将时域特征特征向量S、频域特征特征向量P、能量矩特征向量L和样本熵特征向量SE结合构造为多域特征集T。

T=[S,P,L,SE]

(6)

1.2 基于UMAP算法改进的多域特征提取方法

原始的多域特征提取方法虽然能更好的展现滚动轴承故障信息,但是其构造的特征集维度较高且非线性易产生信息冗余使诊断模型的训练速度变慢精度降低,往往最后得到的诊断结果不理想。

UMAP算法是一种数据信息提取融合的优化算法,通过假设数据均匀流行分布在拓扑空间中将其近似映射到低维空间。由于具有更优越的运算性能、更好的可扩展性同时保留了更多的关键信息,所以UMAP算法可以有效地解决传统多域特征提取方法构造的特征集高维、非线性、信息冗余等问题。UMAP算法的步骤为:

步骤1:求每个数据点xi的k近邻,定义ρi和σi,设:

ρi=min{d(xi,xij)|1≤j≤k,d(xi,xij)>0}

(7)

并设σi为:

(8)

步骤2:使用力导向图布局算法计算xi的加权k邻域图的低维分布:

(9)

式中:a和b是超参数,yi和yj为坐标。

改进后的多域特征提取方法步骤为:

步骤1:提取轴承振动信号时域、频域特征;

步骤2:将轴承振动信号进行CEEMDAN分解提取IMF分量能量矩与样本熵特征并根据相关系数法选取有效特征;

步骤3:将时域特征、频域特征、能量矩特征与样本熵特征组合构造多域特征集;

步骤4:采用UMAP算法对多域特征集进行全局信息提取与融合,将多维特征映射到低维空间;

步骤5:结束算法,输出新的特征集合。

改进后的流程图如图1所示。

图1 改进的多域特征提取方法流程图

2 故障诊断模型

由于传统的多域特征提取方法构造的多域特征集存在维度过高、信息冗余和非线性等问题导致其占用计算资源过大,分类精度不足,所以对训练故障诊断模型的智能算法要求过高。因此本节采用前文所提出的基于UMAP算法改进的多域特征提取方法通过基础的支持向量机构造滚动轴承故障诊断模型,避免分类算法过于复杂、模型计算时间过长、诊断准确率降低的情况。具体流程如图2所示。

图2 滚动轴承故障诊断流程图

由图2可知,本文的滚动轴承故障诊断流程主要分为3部分:

(1)对获取的轴承振动数据进行CEEMDAN分解等基础处理;

(2)采用基于UMAP算法改进的多域特征提取方法求解多域特征的低维映射构造低维特征集;

(3)将构造好的低维特征集输入到支持向量机中进行诊断模型训练与故障信号识别。

3 案例分析

实验验证数据来自某大学的滚动轴承振动信号实验数据集,选取负载2 hp,转速1750 r/min,故障直径0.177 8 mm,采样频率12 kHz,外圈滚道故障在6点钟位置的驱动端轴承故障数据进行测试。

4种轴承振动信号如图3所示。每种样本状态取200组共800组数据,每组数据1024个点。

(a) 健康状态 (b) 内圈故障状态

根据图2所示的流程图对每组轴承振动信号进行多域特征提取。经过实际计算CEEMDAN分解的各组信号的前4个IMF分量与原始信号的互相关系数均大于0.1,所以选取各组前4个IMF分量作为有效分量提取能量矩与样本熵特征。在图4中可见各个轴承样本状态分解后的前4个IMF分量,4种轴承样本状态的振动信号IMF分量波形有明显的不同。

由图5可知,UMAP算法改进的多域特征提取方法效果最好,其特征集在三维与二维中各状态的数据点聚集在一起且清晰可分,t-SNE算法改进的多域特征提取方法构造的特征集在三维与二维中勉强可分但有少部分数据接触在一起发生混叠,而PCA、KPCA与MDS三种算法改进的多域特征提取方法构造的特征集在三维与二维中均有特征数据点混叠发生。

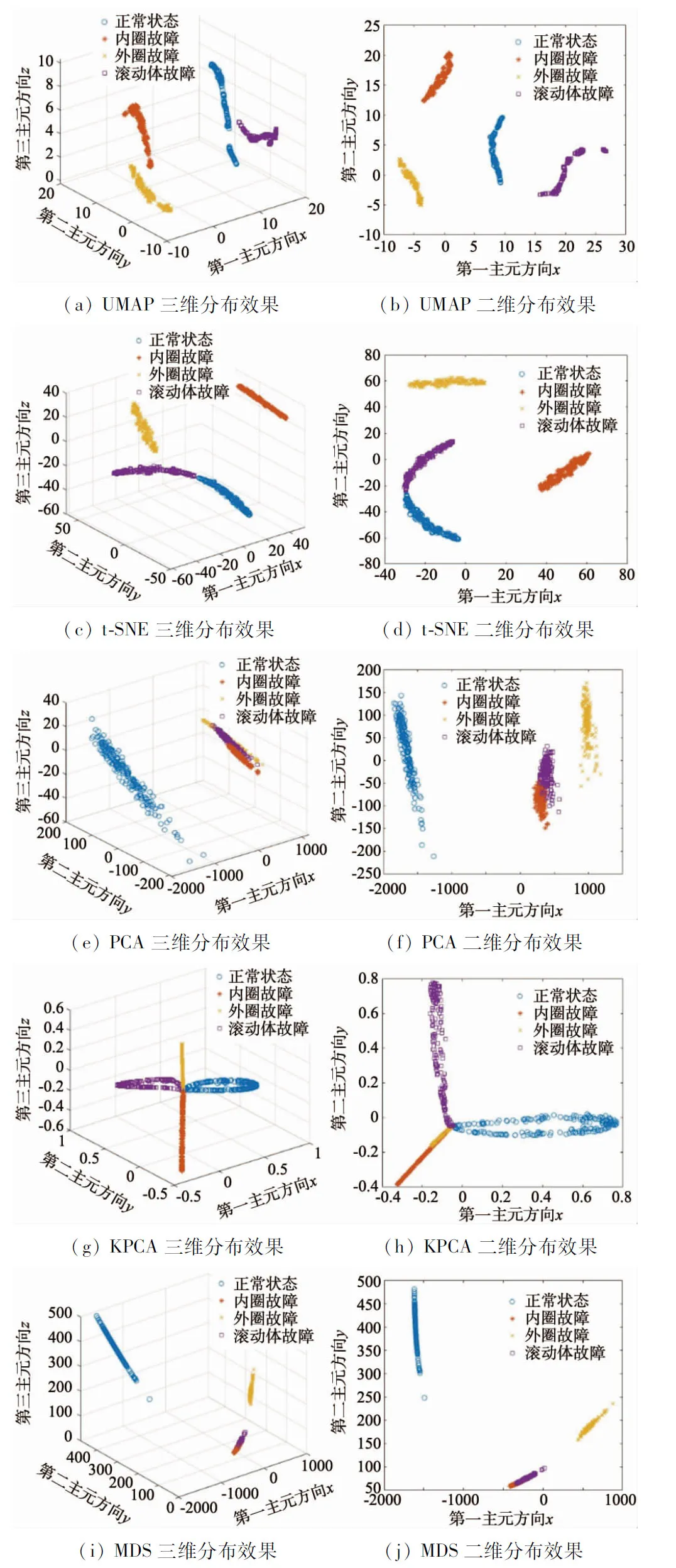
图5 不同优化算法效果对比图

将通过各改进算法得到的特征集输入到支持向量机中进行训练,采用五折交叉验证对训练得到的模型进行检验并对比。

由表2和表3可知,基于UMAP算法改进的多域特征提取方法计算速度较快且识别准确率为100%。虽然t-SNE算法改进后的多域特征提取方法识别结果较为准确但计算时间过长,PCA、KPCA、MDS三种算法改进的多域特征提取方法识别准确率较低,而传统的多域特征提取方法识别准确率为89.3%不能实现轴承故障的完全识别且训练时间较长。

表2 各方法准确率对比

表3 各方法计算时间对比

因此基于UMAP算法改进的多域特征提取方法在诊断的准确率与计算速度方面都优于其他方法,验证了本文所提方法的有效性。

4 结论

本文提出了一种基于统一流行逼近与投影算法(UMAP)改进的多域特征提取方法并通过支持向量机与轴承振动信号数据集验证了该方法的有效性。实例分析结果表明,基于UMAP算法改进的多域特征提取方法构造的特征集各故障状态特征点清晰可分,相对于其他优化算法和传统多域特征提取方法在计算速度与识别准确率方面均有改善,能准确识别出轴承故障状态。