SLAM精度的向量加权平均自适应调节研究*

蔡 艳,杨光永,陈旭东,徐天奇

(云南民族大学电气信息工程学院,昆明 650000)

0 引言

随着社会不断发展,越来越多场合下需要移动机器人在不确定的陌生环境中进行自主工作。因此,SLAM(simultaneous localization and mapping)即瞬时定位与建图,成为了机器人导航与定位领域的一项重要技术[1]。目前SLAM的求解方法可大致分为基于卡尔曼滤波器的方法、基于粒子滤波器的方法、基于图优化的方法[2]。粒子滤波(particle filter,PF)基于蒙特卡罗方法,易实现且具有非线性[3-4],是常用于解决SLAM问题的方法之一。

由于粒子滤波算法基于蒙特卡洛方法,因此要达到所需估计精度需要大量的粒子,而粒子数量越多,算法时间复杂度越高;此外,重采样会不断拷贝权重较大的样本,抛弃权重较小的样本[5],易导致样本多样性下降,出现粒子退化的问题。而进化问题和粒子滤波器本质上都是通过评价、选择和更新的迭代过程获得最优解[5],因此很多研究者采用进化方法来解决粒子滤波器存在的问题。如陈志强等[6]将帝王蝶算法融入粒子滤波中,引入自适应遗传参数提高算法精度;田梦楚等[7]采用萤火虫算法智能优化粒子滤波,利用萤火虫群体的优胜劣汰机制及个体的吸引和移动的行为,提高粒子滤波的预测精度;刘海涛等[8]利用遗传算法改进粒子滤波,提出对低权值粒子的改进的智能粒子滤波处理策略,以此提高精度等。上述方法均提高了粒子滤波算法的性能,但大多都是通过经验值控制智能算法迭代次数,易造成优化不足或过度优化而引起估计精度降低的问题。

受这些方法的启发,本文引入向量加权平均算法这一智能算法来改善粒子滤波器的性能。向量加权平均算法(weighted mean of vectors algorithm,INFO)是一种新型智能优化算法[11],该算法通过向量的不同加权平均规则,来达到寻优目的。相比之前多数的智能算法,该算法的搜索精度、收敛速度、稳定性更佳[11],为避免仅依靠经验值设置迭代次数,引入自适应调整迭代次数策略。

本文为进一步提高PF算法的性能,引入自适应调整迭代次数的INFO收敛速度快、寻优能力强的特性更新预测粒子集,提高粒子集质量;当粒子密集度过高时,加入次优粒子的作用合理调整粒子集分布,多样化粒子;根据自调INFO获取的最优解调整预测粒子集,使粒子集在权重计算前就更接近期望值,以此提高路径和路标的估计精度;在重采样阶段通过重组粒子集来增加粒子多样性。

1 自调向量加权平均优化的粒子重组PF

1.1 自调向量加权平均算法

向量加权平均算法(weighted mean of vectors algorithm,INFO),是一种新型智能优化算法[11]。该算法通过向量的不同加权平均规则,来达到寻优目的,具有寻优能力强,收敛速度快等特点。为自适应调整迭代次数与粒子分布,提出一种自调INFO算法,在原算法基础上增加了粒子密度监测与自调粒子分布策略,该算法包括以下5个阶段。

(1)粒子更新规则阶段。AINFO使用基于均值的规则(MeanRule)更新粒子的位置,此外,为了提高全局搜索能力,在更新规则算子中加入了收敛加速部分。更新规则的主要公式如式(1)和式(2)所示。

(1)

(2)

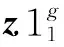
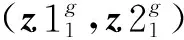
(3)

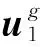
(3)局部粒子搜索阶段。AINFO使用局部搜索阶段来防止陷入局部最优解。根据该算子,如果rand<0.5,则可以围绕生成一个新的粒子。新生成粒子表达式为:

(4)

(4)粒子密度监测阶段。为避免仅依赖经验值设置迭代次数造成优化不足或过度优化的问题,引入粒子密度监测阶段。实时监测最优粒子附近的粒子密度,当密度达到阈值时,停止迭代。粒子密度计算表达式为:

(5)

式中:Nbest表示最优粒子周围的粒子数,rbest表示密度半径,find操作表示查找密度半径内的粒子数量。

(6)

式中:ρbest表示最优粒子周围的粒子密度,N表示粒子总数。

(5)自调粒子分布阶段。当粒子集过于集中于最优粒子附近时,考虑次优粒子的影响自适应调整部分粒子分布,从而增加整体粒子多样性。当粒子密度超过所设置的最大集中密度时,根据下式调整部分粒子分布:

(7)

式中:σ为[0,1]之间的随机数。

1.2 粒子重组重采样

本文针对粒子滤波算法在重采样阶段去除小权值粒子而降低估计性能的问题,在重采样阶段设计如下粒子筛选策略:

(1)计算有效粒子数Neff以及粒子权重,并将权重按降序排列;

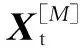
(8)

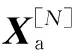
1.3 基于自调向量加权平均的粒子重组粒子滤波

针对传统粒子滤波算法存在需要大量粒子来提高精度与粒子多样性缺失的问题,本文引入INFO算法对其进行优化。为避免优化不足或过度优化且减少时间复杂度,采用自适应调整迭代次数策略;为增加粒子多样性引入自适应调整粒子集分布与重采样阶段粒子重组策略。算法步骤为:

步骤1:初始化粒子集X0,每个粒子初始权重为w0=1/M;

步骤2:从proposal分布中采样粒子集,t时刻的采样粒子集Xt如下:

Xt～p(xt|xt-1,ut)

(9)

步骤3:AINFO优化,更新粒子集:

①根据粒子集初始化向量集;

②对粒子集中所有粒子根据式(9)计算适应度函数;

③粒子更新规则阶段,根据式(1)、式(2)更新粒子位置;

④粒子合并阶段,通过更新规则阶段得到的粒子根据式(3)合并成新的粒子;

⑤局部粒子搜索阶段,如果rand<0.5,则根据式(4)生成一个新的粒子;

⑥粒子密度监测阶段,根据式(5)、式(6)计算粒子密度,当密度大于阈值ρth时,停止迭代;

⑦自调粒子分布阶段,当粒子密度大于ρmax时,根据式(7)调整粒子分布。

步骤4:根据AINFO的输出更新粒子集分布;

步骤5:计算粒子权重;

步骤6:粒子重组重采样,根据式(8)重组粒子集;

步骤7:迭代更新预测值,根据下式输出预测值。

(10)

基于AINFO优化的粒子重组粒子滤波算法流程图如图1所示。

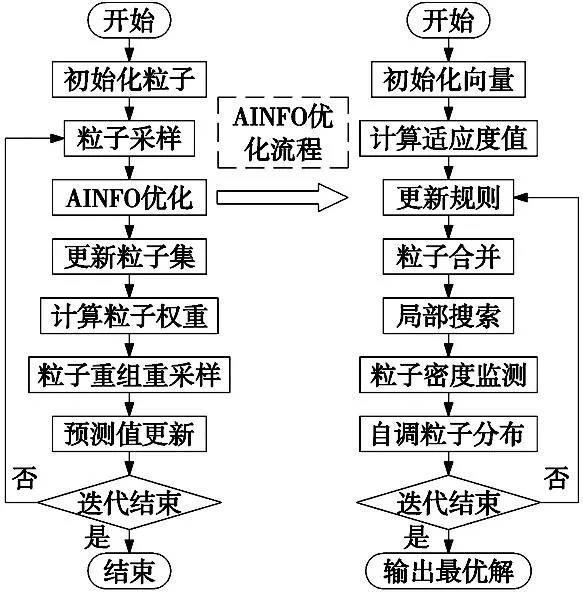
图1 基于AINFO的粒子重组PF算法流程图

2 仿真实验

进行仿真实验验证本文算法在SLAM中的估计性能,由于基于粒子滤波的FastSLAM因定位精度较高、鲁棒性较好等特性已发展成SLAM技术的主流算法[12],因此将传统FastSLAM与本文AINFO-FastSLAM算法进行仿真对比实验。

2.1 密度半径设定

引入智能算法优化粒子滤波时,一般设置最大迭代次数,而智能算法迭代过程中具有随机性,仅通过最大迭代次数可能会造成过度优化或优化不足问题。本文引入自适应调整策略,设置粒子密度监测阶段,自适应调整迭代次数。粒子密度的衡量标准取决于密度半径的设定,表1统计了当粒子数为100时,不同时刻不同密度半径下的粒子密度占比值。

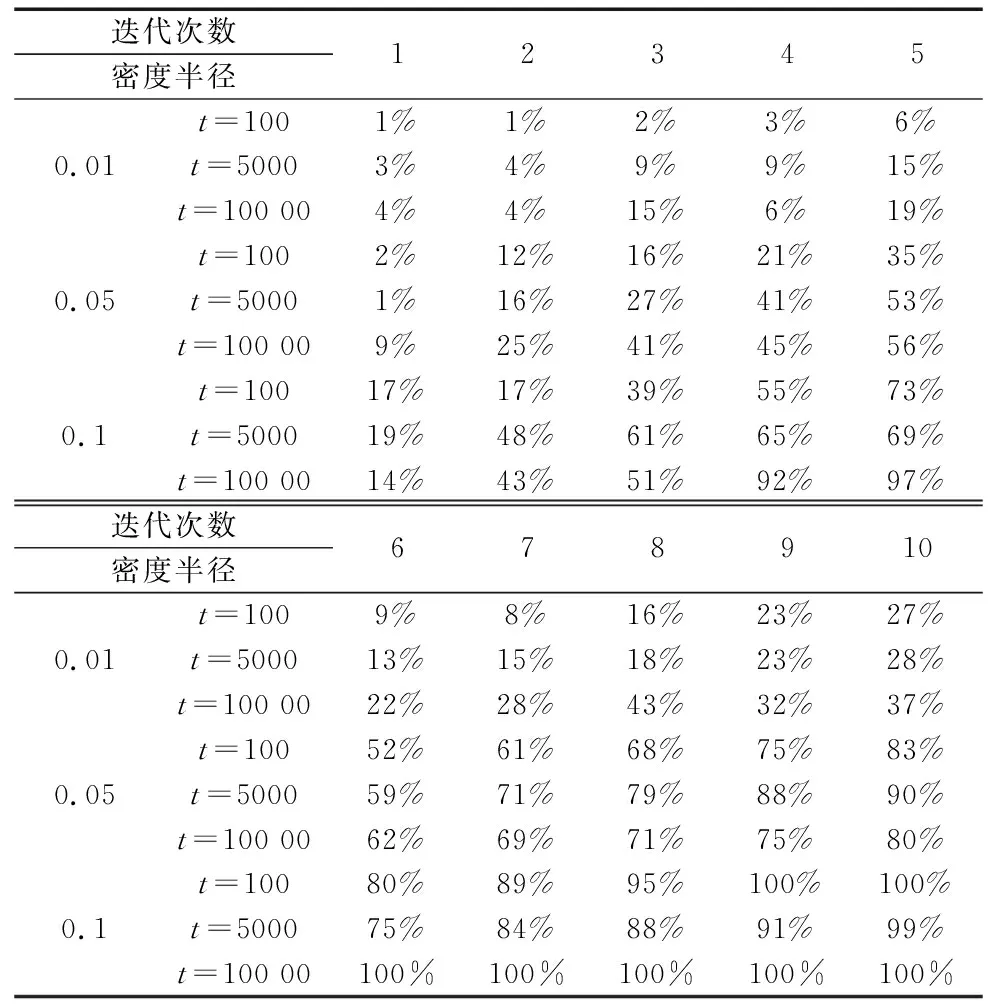
表1 不同时刻不同密度半径下的粒子密度占比

从表1可知,当密度半径为0.01时,粒子密度总体随着迭代次数的增加而增大,但局部存在波动且随着迭代次数增加粒子密度增长较缓慢,达到期望优化程度时间复杂度较高;当密度半径为0.05与0.1时,随着迭代次数的增加粒子密度的增长速度较快,但后者粒子密度在前几次迭代就达到100%,迭代次数过少会导致精度下降问题。当密度半径为0.05时,随着迭代次数的增加,粒子密度增长趋势相对平缓,能较好反映粒子分布情况,因此,本文选取密度半径为0.05。

2.2 自适应调整迭代次数分析

为进一步验证本文算法自适应调整迭代次数的准确性,分别在粒子数为20、50和80的情况下进行30次仿真实验,计算该算法的平均迭代次数,最后计算30次实验的平均迭代次数,结果如表2所示。

表2 不同粒子数的AINFO-PF平均迭代次数

从表2可以看出,随着粒子数目的增加,AINFO-PF算法的平均迭代次数会相应减少,这是因为,粒子数的增加会提高粒子滤波的估计精度,达到期望优化程度的迭代次数会相应减少,由此可见,本文算法可根据当前优化程度自适应调整迭代次数,避免过度优化或优化不足导致的估计精度降低问题,且可自适应减少迭代次数,降低计算复杂度。

2.3 仿真模型

(1)运动模型,本文移动机器人运动模型为:

(11)

式中:[xtytθt]T表示t时刻机器人预测位姿,ΔT为机器人里程计采样时间间隔。

(2)观测模型,描述了机器人观测值与当前位姿估计和环境路标之间的关系。

(12)

式中:dt与βt分别为t时刻机器人观测到的路标距离和角度。

2.4 实验结果及分析

为验证本文算法有较好的估计性能,将INFO-FastSLAM、AINFO-FastSLAM算法与传统的FastSLAM算法进行对比实验,并进行误差对比分析。

根据Bailey开发的SLAM算法通用模拟器[16]设计了尺寸为100 m×82 m,并具有42个路标特征的环境地图及机器人运行参照路径,模拟机器人在真实场景中进行瞬时定位与建图,仿真环境如图2所示,其中黑色星号代表路标,灰色折线代表机器人的控制输入量,即规定路径。灰色圆圈为机器人位姿点,共有14个。仿真环境的移动机器人相关参数设置如表3所示。

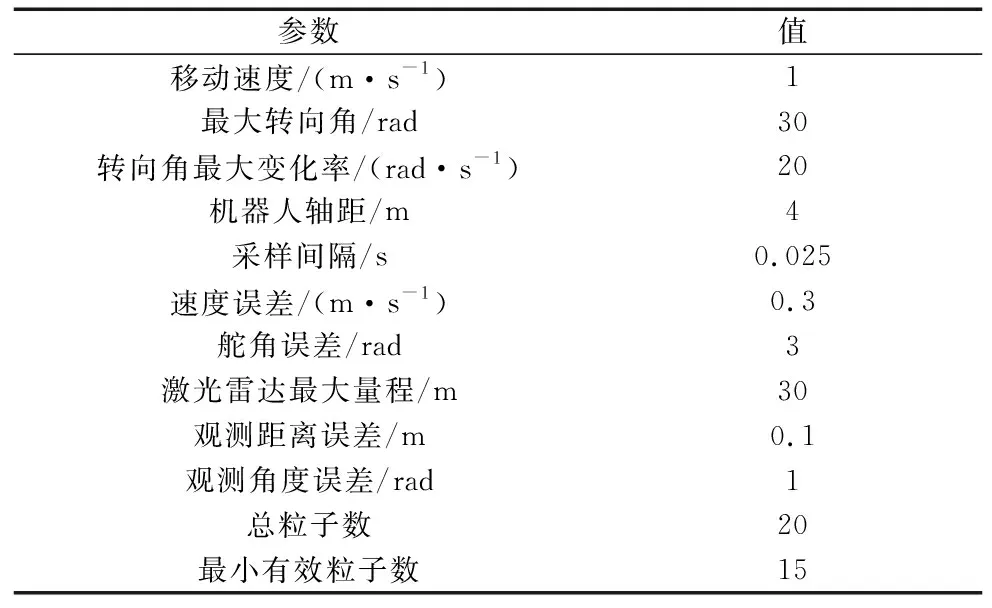
表3 仿真实验机器人参数设置

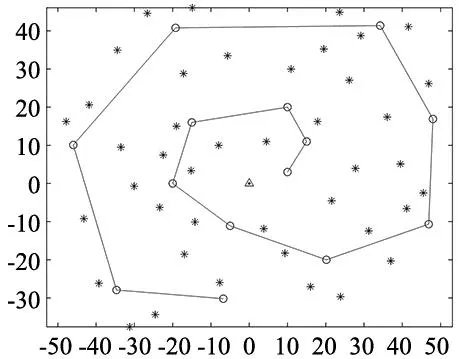
图2 仿真环境地图

设置机器人相关参数后,机器人从坐标原点出发沿预设路径逆时针运动一圈,通过运动模型与观测信息实现实时定位与建图。仿真实验结果对比如图3所示。

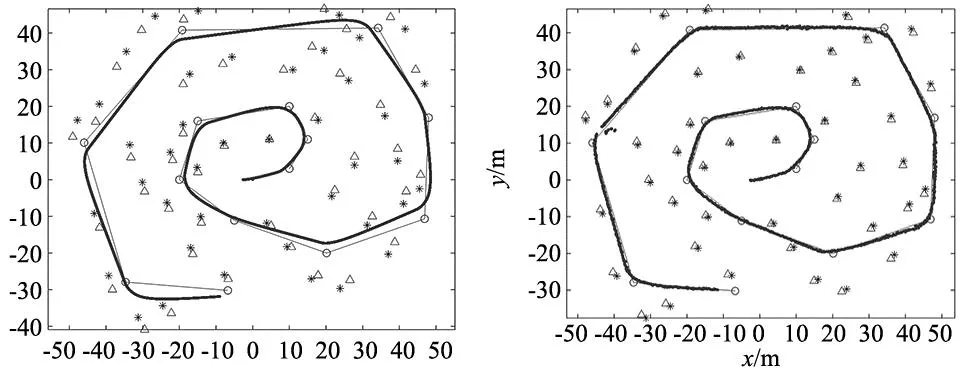
(a) 传统FastSLAM算法预测结果 (b) INFO-FastSLAM算法预测结果

从图3可以看出,传统FastSLAM随着误差的累积,机器人路径随着时间推移误差增大,路标估计也出现较大误差;INFO-FastSLAM与AINFO-FastSLAM的机器人路径与真实路径基本一致,且路标估计的误差明显减少;但INFO-FastSLAM存在估计鲁棒性不佳现象,路径估计会突然偏离真实路径,AINFO-FastSLAM相比INFO-FastSLAM,其路径估计更稳定且误差更小,同时环境路标估计位置与实际路标位置基本一致。其原因在于:INFO-FastSLAM运用向量加权平均优化这一思想优化传统算法,能有效提高路径与路标估计性能,但仅依靠经验值会存在过度优化导致精度下降或优化不够导致误差较大的问题;AINFO-FastSLAM采用自适应调整策略的INFO算法调整预测粒子集,避免了过度优化或优化不足的问题且减少时间复杂度,能实时纠正机器人路径估计,降低路标估计误差。

2.5 实验误差对比

为进一步验证本文算法应用到实际场合中的有效性,在该仿真环境中,分别对传统FastSLAM、INFO-FastSLAM以及AINFO-FastSLAM三种算法进行位姿预测误差对比与路标位置预测误差对比,如图4～图6所示。

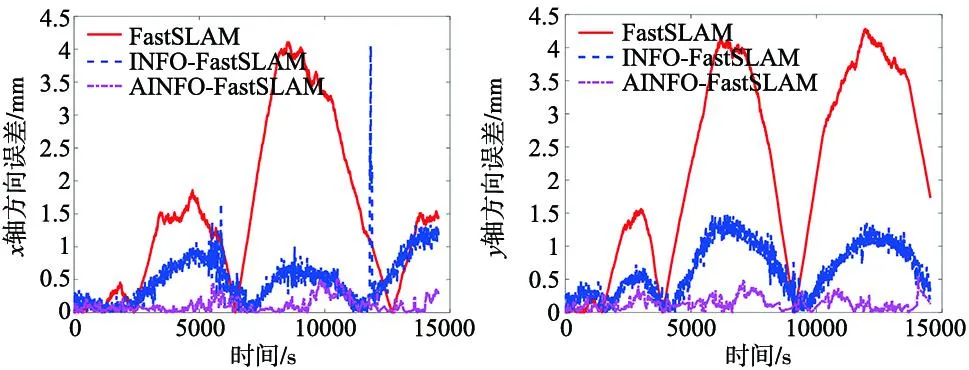
图4 x方向位姿估计误差 图5 y方向位姿估计误差

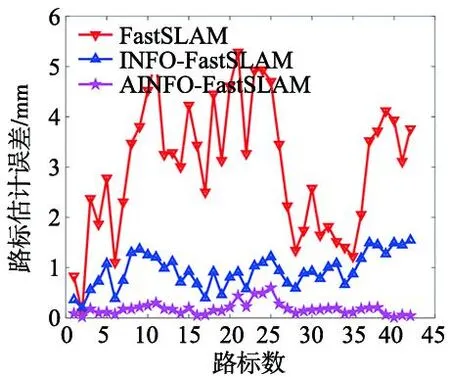
图6 路标位置估计误差

图4和图5为3种算法的位姿预测误差比较图。可以看出,INFO-FastSLAM在x轴的估计误差非常不稳定,相比之下AINFO-FastSLAM的位姿预测误差稳定且更小;从图6可以看出,AINFO-FastSLAM算法的路标位置预测误差相比INFO-FastSLAM算法更小。

考虑到实验结果的偶然性,为进一步证明本文提出的算法性能的优越性,引入均方根误差(RMSE)对机器人路径与路标位置估计进行评价[17],将3种算法分别进行30次仿真实验并取平均值,采用RMSE作为衡量指标,表达式为:

(13)

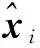
表4 3种算法x轴、y轴、路标位置均方根误差对比

3 结论

本文提出一种基于自调INFO优化的粒子滤波算法,引入自适应调整策略的INFO更新预测粒子集,当粒子密集度过高时,自适应调整粒子集分布,使预测粒子集更快向移动机器人真实位置聚集,提高粒子集质量;在重采样阶段,考虑大权值粒子和部分小权值粒子的共同作用重组粒子集。将该算法应用到SLAM中,仿真实验结果表明,当粒子数为20时,AINFO-FastSLAM相比传统FastSLAM在x轴位姿估计精度提高了78.5%,在y轴位姿估计精度提高了80.3%,路标估计精度提高了81.6%。在同等条件下,该算法定位及地图构建精度更高,综合性能更强。