基于相位稳定的音圈电机鲁棒控制器设计

陈昊男,孟范伟,王重辉

(东北大学秦皇岛分校控制工程学院,秦皇岛 066000)

0 引言

音圈电机因为具有结构简单、响应速度快、便于控制等优点而广泛应用于精密伺服系统中。然而在这类系统中,系统性能往往会受到机械谐振、负载扰动、工况变化等因素的影响,因此需要设计控制器提高系统的抗干扰能力及鲁棒性来减小这些因素带来的不良影响[1]。

为了提高精密伺服控制系统的性能,国内外学者展开了广泛的研究。CHEN等[2]将复合非线性反馈控制应用于精密伺服系统,不仅实现了系统的快速响应,还有效增加了闭环系统的阻尼比,减少线性部分引起的超调。GUO等[3]提出了一种复位最优控制律,相较于传统的时间最优控制而言,设计过程大幅简化,并且明显改善了精密伺服系统的瞬态响应。HAWWA等[4]提出了一种非线性PID控制方案用于设计伺服控制器,利用非线性函数的微分作用调节系统阻尼,有效改善了系统的调节时间并提高了抗干扰性能。白姗等[5]提出一种递归型互补滑模控制器实现音圈电机的位置控制,有效的增加了系统的响应速度并抑制了抖振效果。BASHASH等[6]提出了一种频域数据驱动控制设计方法用于防止后奈奎斯特频率谐振模态混叠,有效提升了系统的跟踪性能。然而这些控制方法大多并未考虑模型参数摄动的情况,从而无法保证摄动系统的鲁棒性能与抗干扰能力。

为此本文提出了一种基于相位稳定的鲁棒控制策略,用于抑制系统的机械谐振与输入干扰,并在模型参数出现摄动的情况下保证系统的鲁棒性能。

1 被控对象模型

对于硬盘驱动器单级磁头定位系统而言,主要通过音圈电机(VCM)驱动磁头进行定位实现读写操作。理想的音圈电机模型本质上可以看作一个双积分器[7],但如果考虑其主导谐振模态,则音圈电机的机械模型如式(1)所示。

(1)

式中:ξmi为谐振模态的阻尼比,ωmi为谐振模态的固有频率,ki为谐振模态的残差。

对于音圈电机模型还需要考虑其电路模型的特性,电路模型一般在低频段具有稳定的幅值与相位特性[8],因此可以近似为一个一阶惯性环节,如式(2)所示。

(2)

式中:ωe为电路系统的带宽。

同时,在精密伺服控制系统中,一般无法忽略时间延迟的影响[9],因此将这部分时间延迟建模如式(3)所示。

Pd(s)=e-Tds

(3)

式中:Td为延迟时间。

综上所述,音圈电机模型包含了机械模型特性,电路模型特性及时间延迟特性,传递函数如式(4)所示。

P(s)=Pm(s)Pe(s)Pd(s)

(4)

模型参数的选取由文献[8]中的硬盘驱动器基准模型给出,具体参数如表1所示。

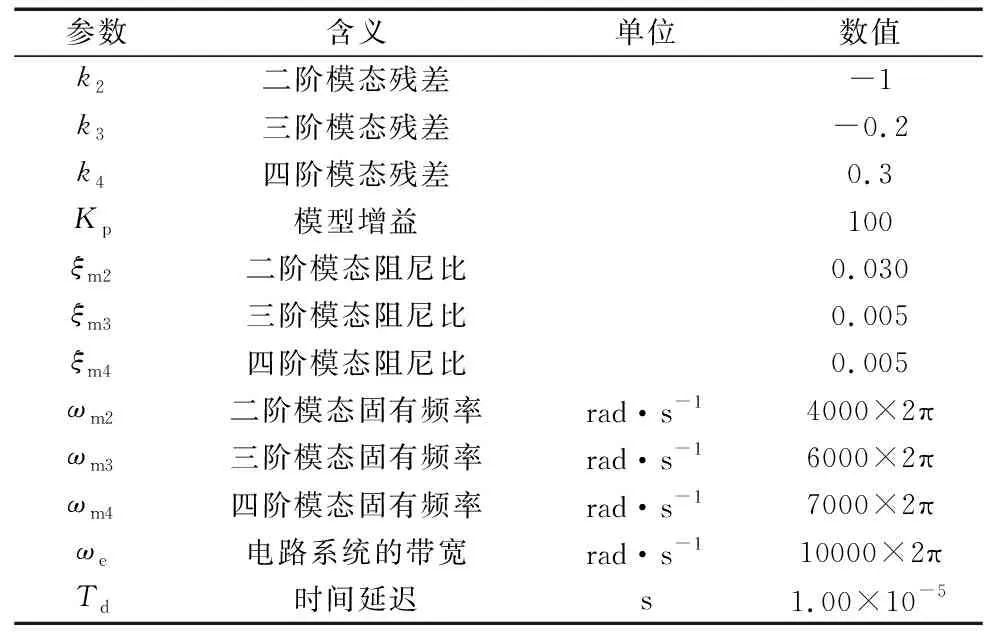
表1 音圈电机模型具体参数

2 鲁棒控制系统设计

控制系统框图如图2所示。图中,P(s)是被控对象,C(s)是用于稳定回路的控制器,F(s)是用于补偿机械谐振的滤波器,df是转矩扰动,e是位置误差信号。

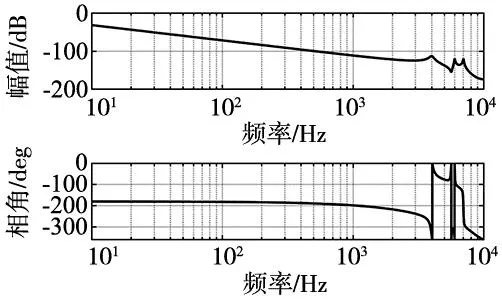
图1 被控对象频率响应

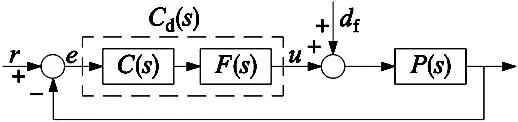
图2 系统控制框图

设计的控制器需要包含以下特性:具有积分特性用于构成Ⅰ型伺服系统;稳定刚体模态的相位超前特性;补偿一阶振动模态的相位滞后;降低具有不稳定相位条件的二阶振动模态的增益。同时,反馈控制系统设计应满足如表2所示的性能指标。

表2 期望性能指标

2.1 相位稳定控制器设计

在伺服控制中使用增益稳定设计的方法来抑制机械谐振会导致系统的相位特性大幅衰减,因此采用改善系统“第二相位裕度”的方法来抑制机械谐振[10]。第二相位裕度一般在系统的幅值频率特性多次穿越0 dB线时定义,其示意图如图3所示。

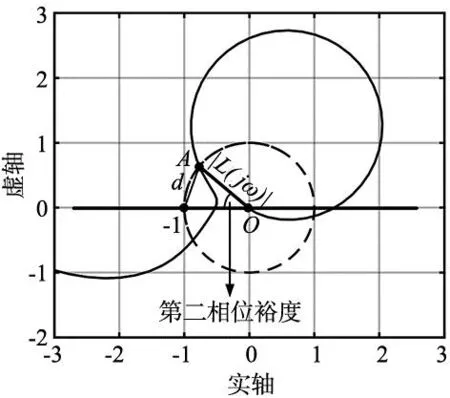
图3 第二相位裕度

定义1:奈奎斯特曲线第一次穿出单位圆时的交点定义为A,原点为O,第二相位裕度即线段OA与负实轴的夹角。

二次穿越点A与(-1,j0)点的距离为:

d1=|L(jω)-(-1)|

(5)

式中:L为系统的开环特性。

如果系统的第二相位裕度过小,则d1也同样会变得很小,这将会使得系统灵敏度函数的幅值|1/(1+L(jω))|变大,从而导致系统的闭环频率响应出现峰值,且系统的响应曲线也将出现振荡。

由此可以看出,相位稳定设计就是在保持一定的系统带宽的同时,通过改善系统的第二相位裕度来避免上述情况的发生。

为了使控制器具有积分特性并且可以稳定刚体模态的相位超前特性,选择使用比例积分-超前(PI-Lead)控制器[11-12]。PI-Lead控制器的形式为一个PI控制器与一个一阶超前补偿器串联,式(6)为PI-Lead控制器的广义表达式。

(6)

式中:Kc是控制器增益,ωcn1是PI-Lead控制器从积分特性变成比例特性的转折频率,ωcn2是PI-Lead控制器从比例特性变成微分特性的转折频率,ωcd是PI-Lead控制器从微分特性变成比例特性的转折频率。各参数的选择规则如下:

ωcn1:决定控制器积分特性强弱的参数。增大ωcn1时,积分特性增强,但相位裕度随之减少。该参数调整应满足当转矩扰动df为阶跃函数时响应也能足够快的收敛。

ωcn2:决定控制器比例特性强弱的参数。增大ωcn2时,能够降低比例特性频段的灵敏度函数增益,但相位裕度随之减少。调整该参数使得低频范围内的灵敏度函数增益尽量降低。

ωcd:决定控制器微分特性强弱的参数。增大ωcd时,相位裕度增加,但幅值裕度减少。调整该参数使得相位裕度、幅值裕度满足性能要求。

Kc:是决定带宽的参数。在设置ωcn1,ωcn2和ωcd之后,调节增益Kc以满足系统带宽的性能要求。

同时设计低通滤波器Flp(s)形式为:

(7)

参数ωlp是用于确定反馈控制器的奈奎斯特频率附近的增益的参数。由于使用双线性变换,因此设定ωlp大于奈奎斯特频率并对该参数进行调整以保证系统在奈奎斯特频率附近的增益足够小。

综上所述,相位稳定控制器的传递函数为:

(8)

为了使控制器具有积分特性并且可以稳定刚体模态的相位超前特性,将控制器参数选择为:

(9)

为了补偿一阶振动模态的相位滞后并降低具有不稳定相位条件的二阶振动模态的增益,选择设计如下改进形式的双T型陷波滤波器[13]:

(10)

补偿一阶振动模态相位滞后的陷波滤波器Fnt1(s)设计为式(11)。

(11)

降低具有不稳定相位条件的二阶振动模态增益的陷波滤波器Fnt2(s)设计为式(12)。

(12)

将陷波滤波器Fnts(s)设置为两个陷波滤波器的串联形式,即Fnts(s)=Fnt1(s)Fnt2(s)。最后,可得反馈控制器为Cd(s)=Cps(s)Fnts(s)。

2.2 基于鲁棒性能条件的控制器参数优化

在伺服控制系统中,公差、温度等因素都有可能会导致被控对象模型的参数出现摄动[14]。鲁棒性就意味着系统抵御这种摄动带来的不确定性对系统动态特性影响的能力。

被控对象P(s)的两种参数摄动情况如表3所示。图4与图5显示了反馈控制系统在模型出现参数摄动时的灵敏度函数幅值响应及Nyquist曲线。

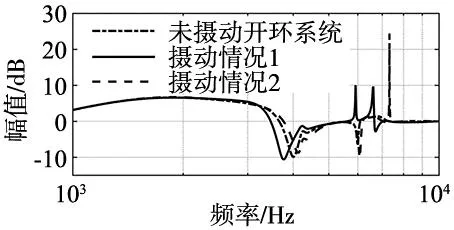
图4 摄动系统灵敏度幅值频率响应

图5 摄动系统Nyquist曲线 图6 摄动系统的幅相频率响应

表3 被控对象参数摄动

由图4及图5可知,在被控对象发生参数摄动时控制系统仍然稳定,但此时灵敏度函数的H∞范数超过7.5 dB,因此不满足期望设计指标,需要根据鲁棒性能条件调整控制器参数来保证参数摄动情况下系统仍满足设计需求。

为了保证摄动系统的鲁棒性能,根据鲁棒性能条件对反馈控制器Cd(s)的参数进行优化。下面对鲁棒性能的幅值条件与相位条件进行推导。

假设系统的结构不确定性Δs包含在标称对象Pn中,仅将非结构不确定性Δus作为乘法不确定性给出,则标称对象Pn可表示为:

Pn(jω)=(1+Δs(jω))P0(jω)

(13)

式中:P0是被控对象中不包含不确定性的部分。

系统标称开环传递函数Ln可表示为:

Ln(jω)=Pn(jω)Cd(jω)

(14)

系统的鲁棒性能条件为[15]:

(15)

式中:W1为鲁棒性能权函数,W3为不确定性权函数。

整理式(15)可得:

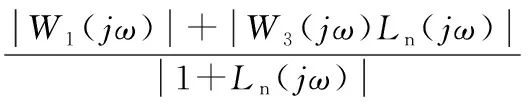
(16)

对Ln使用欧拉变换并代入式(16)可得:

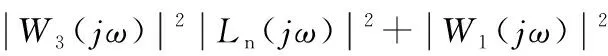
(17)

求解式(17)中的cos(∠Ln(jω))可得系统鲁棒性能的相位条件:

cos(∠Ln(jω))>Q(jω),∀ω

(18)

式中:

(19)

求解式(17)中的|Ln(jω)|可得系统鲁棒性能的幅值条件。

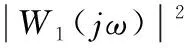
(20)

根据式(18)与式(20)验证使用控制器Cd(s)时控制系统的鲁棒性能,可知系统在5 883.7～5 938.8 Hz,6 489.5～6 643.3 Hz及7 302.7～7 343.22 Hz三个频率范围内不满足鲁棒性能条件式(15),因此需要调整控制器参数以满足系统的鲁棒性能要求。

标称对象Pn及参数摄动后对象的频率响应如图6所示。为了抑制谐振频率下的振动的影响,将性能加权函数W1在频率为4 kHz以上时设置为-3 dB,在频率为4 kHz以下时设置为-7.5 dB。考虑到奈奎斯特频率附近存在的不确定性,不确定性权函数W3在频率为9 kHz以上时设置为12 dB,在9 kHz以下为-40 dB。

根据不满足鲁棒性能条件的频率范围,对反馈控制器Cd(s)的参数作如下调整。调整式(6)中的参数ωcd以增加在高频区域内控制器的相位超前量;调整式(11)的ωn参数用于降低5.92 kHz附近的幅值;调整式(12)的ωn参数用于降低7.3 kHz附近的幅值。

调整后的控制器CpsR(s),陷波滤波器FntR1(s)与FntR2(s)如式(21)所示。

(21)

(22)

(23)

将陷波滤波器FntsR(s)设置为两个陷波滤波器的串联形式,即FntsR(s)=FntR1(s)FntR2(s)。则鲁棒控制器变为CdR(s)=CpsR(s)FntsR(s)。

3 仿真分析

使用鲁棒控制器CdR(z)=CpsR(z)FntsR(z)进行仿真,其中CpsR(z)通过对CpsR(s)双线性离散化得出,FntsR(z)通过对FntsR(s)匹配z变换离散化得出,并设置采样时间Ts=5×10-5s。

控制器参数优化前后系统的性能指标如表4所示,可以看出控制器参数优化后,第二相位裕度提升了8.1%,其它性能指标略有下降但仍满足性能要求。

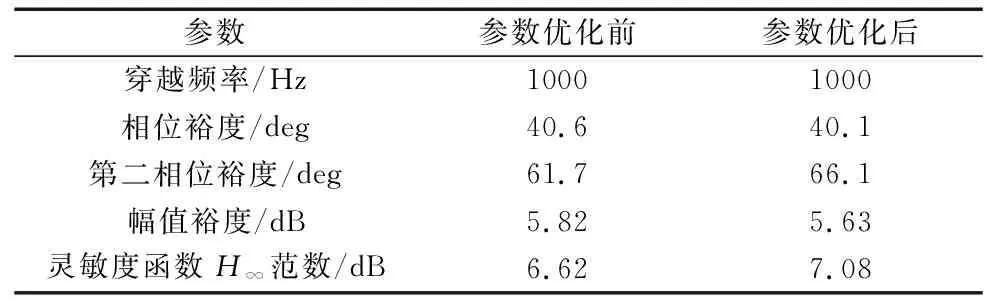
表4 控制系统性能

图7显示了系统的开环频率响应,经过控制三阶模态的幅值得到了有效的抑制。图8显示了系统的Nyquist轨迹,从图8可以看出系统的一阶与二阶谐振模态的奈奎斯特轨迹远离(-1,j0)点,保证了系统的稳定性。

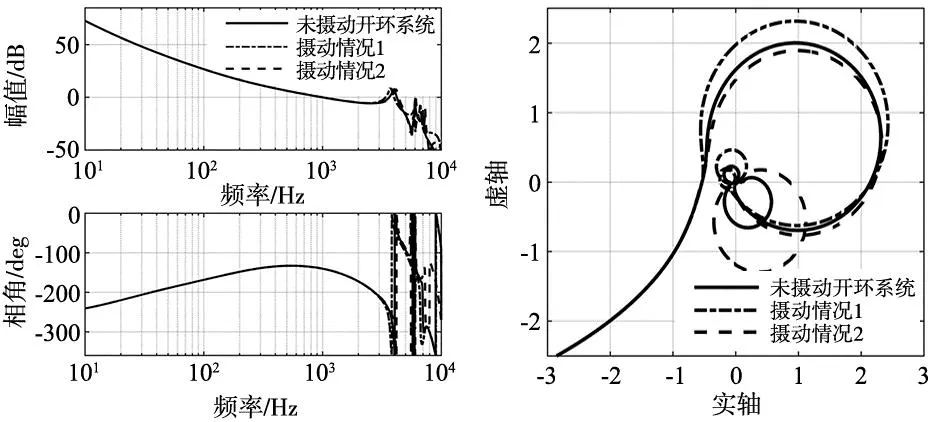
图7 系统的开环频率响应 图8 改进后的系统Nyquist曲线

图9与图10显示了改良后系统的灵敏度与补灵敏度的幅值频率响应。从图中可以看出灵敏度函数幅值在工作频段内满足|W1Sn<1|,补灵敏度函数幅值在工作频段内满足|W3Tn<1|,因此满足鲁棒性能条件(15),同时系统的一阶与二阶谐振模态的灵敏度幅值均小于0 dB,说明系统具有鲁棒性能。

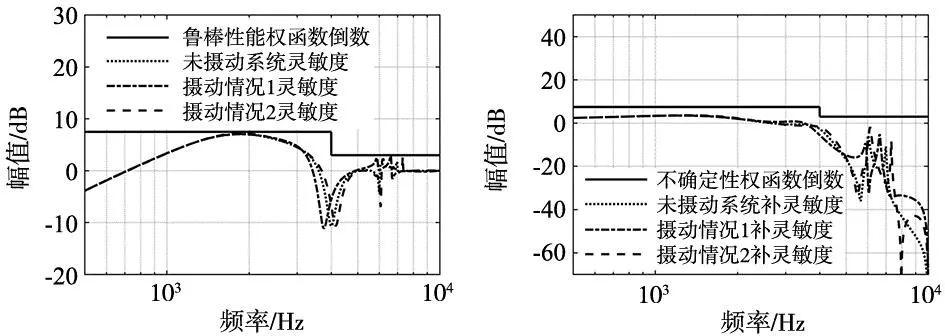
图9 摄动系统的灵敏度函数幅值频率响应 图10 摄动系统的补灵敏度函数幅值频率响应

接着,使用平均值为0.01 N、最大振幅为0.005 N的随机信号作为转矩扰动df对控制系统进行仿真。图11表示了输出y的时间响应,由于控制器所具有的积分特性,在0.05 s时控制量y达到目标值r附近。图12为通过离散傅立叶变换(DFT)求出的振幅频谱的频率响应,由图11及图12可知,控制系统可以有效抑制各谐振模态的振动。

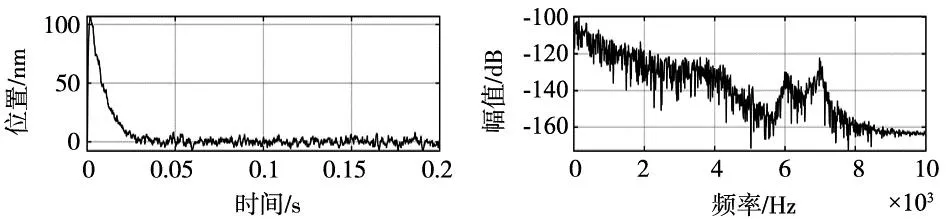
图11 输出y的时间响应 图12 振幅频谱频率响应

4 结论

为了解决传统增益稳定设计方法中出现的系统相位特性衰减与输入扰动出现振荡的问题,本文提出了一种相位稳定设计方法,通过引入第二相位裕度有效抑制系统机械谐振。针对模型的参数摄动通过鲁棒性能条件优化控制器参数,满足了系统的鲁棒性能要求。