基于改进正余弦算法的机械臂轨迹规划*

潘明章,潘 雷,李昌伦,梁 科,姚博炜

(1.广西大学机械工程学院,南宁 530004;2.柳州赛克科技发展有限公司,柳州 545005)

0 引言

轨迹规划是机械臂运动控制的基础。随着工业自动化的不断发展,机械臂的应用环境也愈发复杂,现有的轨迹规划算法正在向着智能化的方向发展。高性能的轨迹规划算法使机械臂运行更平稳,工作效率更高,使用寿命更长。因此,轨迹规划算法得到了国内外专家和学者的广泛关注和研究,许多以时间最优、能量最低和冲击最优为目标的轨迹规划算法被提出[1-3],而其中时间最优轨迹规划由于其广泛且重要的应用价值成为深入研究的热门话题。

关节空间中的3次多项式插值的轨迹规划方法由于计算简单得到了广泛的应用,而其所产生轨迹会使机械臂的关节角加速度会突变,突变意味着驱动力的不连续,这会导致机械振动现象的发生从而降低了机械臂的使用寿命和控制精度。针对这一问题,可以通过增加轨迹插值多项式的阶数来解决,如5次多项式插值,但是每一段轨迹都采用5次多项式插值会导致运算量大幅增加。因此XU等[4]使用3-5-3多项式插值来在上述两种插值方法中取得良好的折中,然而他们没有对插值时间进行优化,所生成的插值轨迹作业效率低。由于多项式插值的阶次高,缺乏凸包,传统方法难以对插值时间进行优化,于是利用智能优化算法进行时间最优轨迹规划成为一个有价值的研究方向。常用的智能优化算法包括粒子群算法[5]、遗传算法[6]和差分进化算法[7]等。但是相较于正余弦算法[8],这些算法参数结构复杂且收敛速度较慢。

正余弦算法因其出色的性能被广泛地应用在各领域中。马莹莹等[9]将正余弦算法运用于机器人的路径规划中以增强探索性能。郎春博等[10]提出改进的正余弦算法来解决多阈值图像分割方法计算量大、分割精度低的问题。王庆等[11]针对含风能的经济排放调度问题,提出了一种混沌正余弦算法以最小化发电成本和碳排放量。正余弦算法的相关研究在众多领域已取得大量成果,但尚未应用于机械臂的轨迹规划问题中。

本文提出了一种基于改进正余弦算法的机械臂时间最优3-5-3多项式插值的轨迹规划算法。该算法在迭代过程中通过平衡因子动态调整当前解和当前最优解之间的权重,加强了局部开发的能力,此外通过引入Lévy飞行改善传统正余弦算法容易陷入局部最优的不足,提高了收敛速度。以UR5e机械臂为研究对象,根据机器人运动学确定多项式插值函数,在一系列约束下使用改进正余弦算法优化插值时间。通过实验验证所提出算法的有效性,并与其他先进的优化算法进行了对比。

1 机械臂运动学模型与多项式插值

1.1 机械臂运动学建模

机械臂的运动学模型是轨迹规划的基础。在绝大多数机械臂应用场景下,都需要根据机械臂末端执行器的位姿来获取各关节的角度位置,从而完成任务空间的运动。本文以UR5e协作机器人为研究对象,机器人实体如图1所示,通过D-H参数法来对其进行运动学建模,D-H参数如表1所示。

表1 UR5e的D-H参数

图1 UR5e机械臂

1.2 3-5-3多项式插值

为了使机械臂在任务空间中完成对指定运动,可以对任务的起点,第一个中间点,第二个中间点和终点进行逆运动学求解,得到每个关节的角度,然后通过3-5-3插值完成轨迹规划。具体的插值方法如下:

(1)

式中:qi1(t)代表机械臂第i个关节第j段的轨迹,aijk代表机械臂第i个关节第j段轨迹插值多项式的k次项所对应的系数,t1、t2、t3分别为3段轨迹的执行时间。插值所生成的轨迹还应满足以下条件:

(1)4个插值点的各关节角度已知;

(2)起点和终点对应的各关节角速度和角加速度为0;

(3)整个轨迹过程中各关节角速度和角加速度连续。

现在,我们可以求解出插值多项式中所有的未知系数,具体过程为:

a=A-1·θ=[a1a2a3]

(2)

式中:

θ=[0 0 0 0 0 0θi40 0θi10 0θi3θi2]T

2 改进正余弦算法

2.1 传统正弦余弦算法

正弦余弦算法(SCA)是一种新颖的基于种群的随机优化算法,其仅利用正弦和余弦函数的波动性和随机性作为实现算子的设计目标来搜索和迭代最优解。与遗传算法,粒子群算法,布谷鸟算法等众多智能优化算法相比,正弦余弦算法具有参数少、结构简单、易实现、收敛速度快等优点,在实际应用中具有较优的性能。其优化迭代过程可分为全局搜索和局部开发两个阶段。在全局搜索中,对于当前解集中的解施加较大的随机波动来搜索解空间中的未知区域;在局部开发中,对当前解施加微弱的随机扰动来充分搜索当前解的邻域。具体的迭代方程分为以下正弦迭代和余弦迭代方程两种,由式(3)所示。

(3)

(4)

式中:xi(t)表示解个体在第t次迭代时在第i维度的分量,pi(t)表示在到第t次迭代为止的所有解集合中的最优解在第i维度的分量。参数r1由式(4)定义,用来实现全局搜索和局部开发的平衡和切换,其中a是一个常数,通常被设置为2,t和T分别为当前迭代次数和最大迭代次数。参数r2～U[0,2π]描述了当前解向当前最优解更新时移动的方向。参数r3是范围为[0,2]的随机数,为当前最优解带来随机权重以强调或者忽略最优解在定义移动距离时的影响效果。参数r4是[0,1]的随机数,使迭代在正弦更新和余弦更新之间随机切换。

2.2 改进的位置更新方程

正弦余弦算法和其他基于种群的优化算法一样,需要平衡全局搜索和局部开发。在传统的正弦余弦算法中,解的位置更新方程仅仅将当前最优解用于随机确定到下一搜索区域的距离,而没有利用当前最优解的位置信息,导致SCA整体更倾向于全局搜索,算法的收敛性较差。因此,针对SCA的上述不足,本文提出了一种平衡权重更新机制,充分利用当前最优解的位置信息来加强算法的局部开发能力,设计了一个改进的位置更新方程,由式(5)所示。

(5)

式中:λ是平衡因子,由式(6)描述,其功能是调整当前最优解和当前解之间的权重。

(6)

式中:fit(p(t))和fit(x(t))分别为当前最优解和当前解的适应度值,与式(3)相比,式(5)强调了当前最优解的位置信息,而部分淡化了当前解的位置信息,这使得SCA更加专注于当前最优解附近的区域,加强了局部开发能力。此外,为了避免过度的局部开发,引入平衡因子λ,利用当前最优解和当前解的适应度值来动态调整其各自权重。当λ较小时,当前解与当前最优解之间存在较大差异,下一个搜索区域将更多地集中于当前最优解附近,相反,当λ较大时,当前解很接近当前最优解,下次搜索将加强对当前解自身位置附近区域的开发。

2.3 混合Lévy飞行策略

Lévy飞行理论自被提出以来[12],因其步长为概率分布呈重尾分布的随机游走,已被广泛应用于智能优化算法中来提高算法的搜索能力。正余弦算法通过两个相互排斥的正余弦方程来搜索迭代寻找最优解,然而在实际应用中,这种搜索过程很容易陷入局部最优的困境。因此,针对这一问题,本文将Lévy飞行的随机游走策略融入到正余弦算法中,在式(5)的基础上作出改进,将位置更新方程分为3个方程,如式(7)所示。

(7)

式中:c是常参数,用来调整3个更新方程的比重;randn是步长缩放因子,为均值为0,方差为1的服从正态分布的随机数;Levy(xi(t))描述了步长服从Lévy分布的随机游走,游走的随机步长采用Mantegna提出用正太分布求解随机数的方法来求解[13],其模型为:

Levy(xi(t))=s·(pi(t)-xi(t))

(8)

(9)

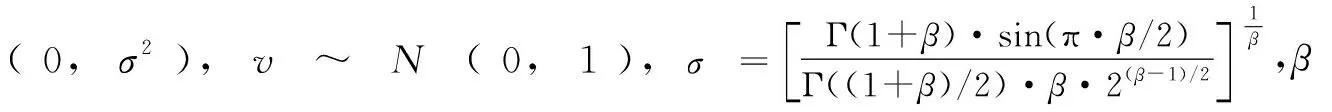
3 基于改进正余弦算法的轨迹优化

时间最优轨迹规划的最终目标是找到一条沿着设定路径的最快可行轨迹,来提高机械臂的工作效率。针对机械臂的最优时间轨迹规划问题,本文采用“3-5-3”多项式来进行轨迹插值,通过所提出的改进SCA算法来优化每段轨迹的运行时间t1,t2,t3。考虑到在真实环境中,机械臂受到自身的运动学和动力学的物理极限的限制,将优化问题的约束条件设置为:

(10)

式中:qi(t)(t=1,2,…,n)代表机械臂第i个关节在t时刻的角度,n为机械臂的关节数,Qimax、Wimax、Aimax分别为机械臂每个关节的最大角度,最大角速度和最大角加速度。

为了弃除不满足约束条件的解并评价迭代过程中解的优劣程度从而更新最优解,本文使用如下的适应度函数:

(11)

式中:x(t)表示解个体(t1,t2,t3),inf表示无穷大。

改进SCA算法针对六轴机械臂时间最优轨迹的优化步骤为:

步骤1:设置算法中的基本参数:种群数量N,最大迭代次数T,Lévy飞行的指数参数β,比重常参数c。设置机械臂各个关节3段轨迹的运行时间(t1,t2,t3)的上下限,随机初始化种群。设置机械臂各关节角度,角速度和角加速度的限制;

步骤2:求解插值多项式,判断种群中每个个体解是否超出约束限制,并计算适应度值;

步骤3:根据适应度更新当目前未知的最优解,并记录其对应位置;

步骤4:更新算法参数r1,r2,r3,r4,λ,根据式(5)计算下一次迭代的种群中每个个体的位置;

步骤5:判断新个体位置是否超出所设置的范围,对超出范围的个体重新进行初始化;

步骤6:判断是否达到最大迭代次数,若已达到,则结束迭代;若尚未达到,则返回步骤2继续迭代;

步骤7:程序完毕,得到各关节的时间最优轨迹,选取每段轨迹中各关节所需完成时间的最大值作为所有关节的执行时间,使所有关节都能同步完成每一段轨迹,以保证机械臂末端能够到达每一个所设置的任务点。

4 仿真实验与结果分析

为了验证所提出的算法的正确性和有效性,本文以UR5e机械臂为实验对象进行了3-5-3多项式插值并使用上述改进SCA算法对所生成的各关节轨迹进行时间最短优化。为了模拟实际任务需要,在任务空间中设置了起点X1、第一个中间点X2、第二个中间点X3和终点X4的位置坐标分别为(400,300,300)、(225,175,200)、(-125,-75,0)和(-300,-200,-100),姿态固定不变,并通过逆运动学得到各关节在以上4个插值点的角度,各关节经过的角度信息如表2所示。

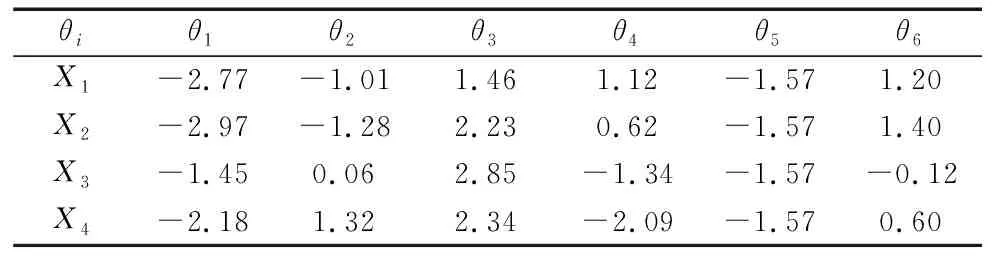
表2 各关节经过的角度信息 (rad)

设置种群数量N为40,最大迭代次数T为500,(t1,t2,t3)在[0,3]的范围内初始化。设置机械臂关节物理限制最大角度Qimax=2π,最大角速度Wimax=3 rad/s,最大角加速度Aimax=10 rad/s2。在改进SCA算法中,Lévy飞行的指数参数β设置为1.5,取比重参数c为0.3。优化过程中适应度值的变化曲线如图2所示,各关节优化后的每段轨迹的运行时间如表3所示。优化后机械臂各关节的角度,角速度和角加速度曲线如图3所示。

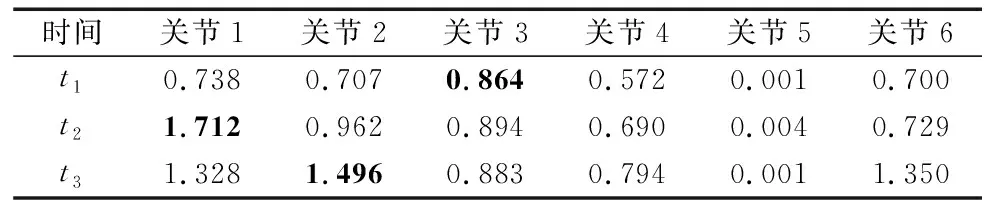
表3 各关节优化后的每段轨迹的运行时间 (s)

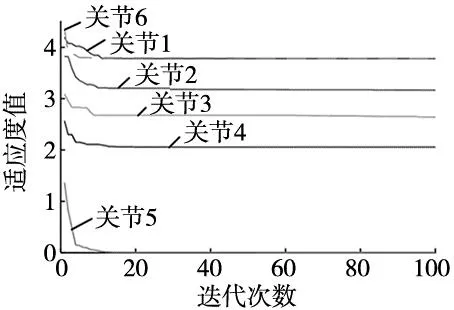
图2 改进SCA的各关节迭代图

根据以上实验结果,可以看出改进SCA算法能够在满足所设置的机械臂各关节约束的条件下,保证所生成轨迹对应的各关节角度、角速度、角加速度曲线平滑无突变,完成了机械臂的时间最优轨迹规划的任务,尽可能缩短了机械臂完成指定任务所用时间,提高了工作效率,验证了本文所提出的改进SCA算法的有效性。

为了进一步验证改进SCA算法的优越性,针对上述机械臂的时间最优轨迹规划问题,依次采用传统正余弦算法(SCA)和3个较优的智能优化算法布谷鸟算法(CS),乌鸦算法(CSA)和粒子群算法(PSO)进行优化,与本文所提出的改进SCA算法进行实验对照,各关节优化迭代过程中的适应度变化曲线如图4所示,完成优化所耗时间如表4所示。所有实验均在lntel(R) Core(TM) i5-10400F CPU @2.90 GHz 16 GB RAM计算机平台上的MATLAB 2020b上进行。

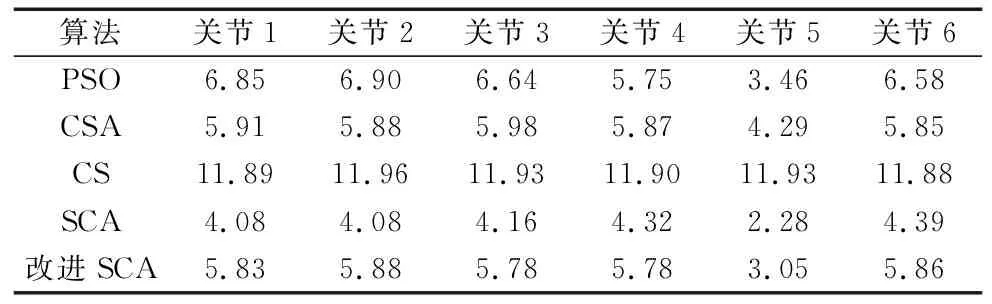
表4 各算法完成优化所耗时间 (s)

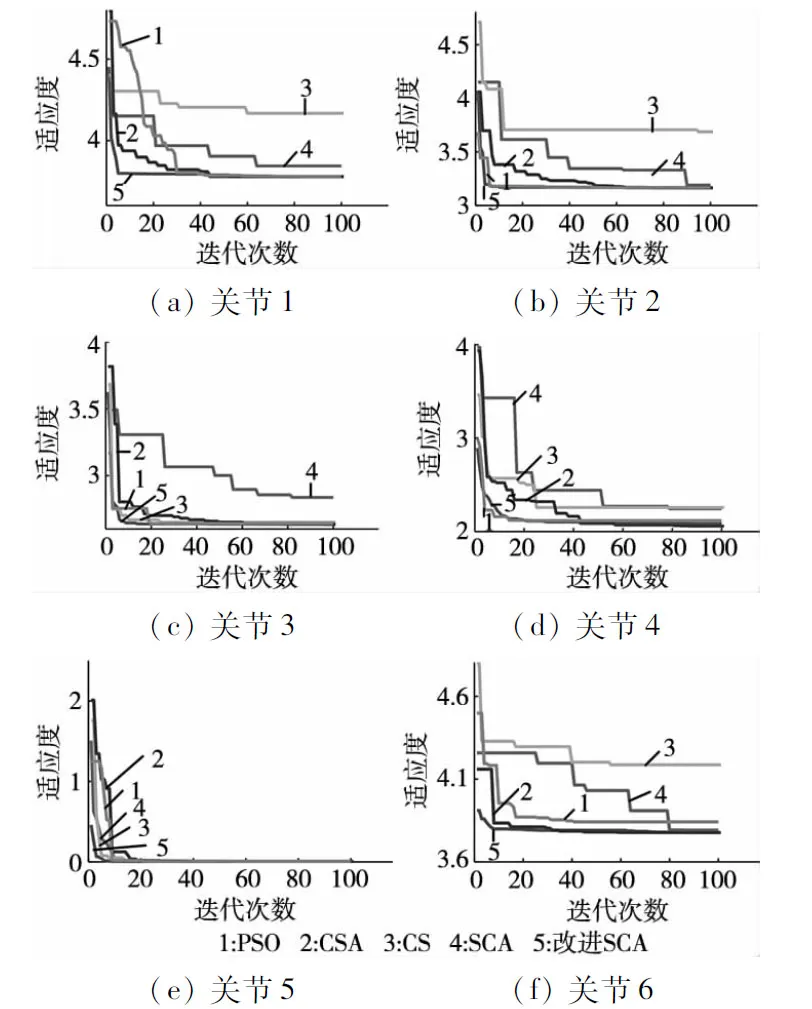
图4 各关节优化迭代图

从图4中可以看出,相较于传统SCA算法改进SCA算法在6个关节上得到的最终轨迹运行总时间更短,具有更强的摆脱局部最优的能力和更高的收敛精度。此外,改进SCA算法在关节1、关节2、关节3、关节5和关节6上的较上述传统4个优化算法都能在更少的迭代次数下收敛到相对最短时间,表现出更快的收敛速度。

从表4中可以看出,虽然改进SCA相较于传统SCA由于额外运算的引入增加了部分优化耗时,但是相较于其他算法,仍表现出出色的优化运行速度。

综合以上实验结果,在六轴机械臂的时间最优轨迹规划问题中,与其他传统优化算法相比,SCA算法运算量小,运行速度快,而改进SCA算法少量牺牲了传统SCA算法的优化速度,但使得算法跳出局部最优的能力和收敛精度得到了显著提高,能够快速得到更优的机械臂运行轨迹。

5 结论

针对关节空间中六轴机械臂时间最优轨迹规划的问题,在3-5-3多项式轨迹插值的基础上,提出了一种改进的正余弦算法来对所生成轨迹进行时间优化。实验表明改进正余弦算法与传统正余弦算法相比,具有更强的跳出局部最优的能力和更高的收敛精度。在与其他优化算法的对比中,改进正余弦算法在保持较高收敛精度的同时表现出更快的收敛速度。经过改进正余弦算法优化后的机械臂轨迹,关节角度,角速度和角加速度变化平滑且均满足所设置的约束条件,缩短了机械臂完成任务轨迹所用的时间,提高了工作效率。