超精密磨削YAG 晶体的脆塑转变临界深度预测

敖萌灿， 黄金星， 曾毓贤， 吴跃勤， 康仁科， 高 尚*

（1.大连理工大学 高性能精密制造全国重点实验室，辽宁 大连 116024；2.华侨大学 制造工程研究院，福建 厦门 361021）

1 引 言

钇铝石榴石（YAG）晶体属于立方晶系，具备良好的光学性能（如光学均匀性、光学透射率等）和热力学性能，在力学性能和化学稳定性上接近蓝宝石晶体，且没有双折射效应［1-3］，广泛应用于制备固体激光器增益介质，在军用和民用领域具有广阔的应用前景［4-7］。工业上主要采用提拉法生产YAG 晶体，该方法生产的YAG 晶体呈棒状，需要经过“外圆磨削-切片-研磨-抛光”的工艺流程获得高面形精度和高表面质量的YAG 晶片［8-10］。YAG 晶体是一种典型的硬脆材料，采用金刚石线锯对YAG 晶棒进行切片加工时，晶片表面会产生大量的切痕、微裂纹等损伤，形成较大深度的损伤层，需要进一步通过研磨和抛光等工艺去除损伤层。其中，研磨工艺存在加工效率低、表面损伤难控制和面形精度不稳定等缺点，会影响后续抛光加工的效率和成本［11-12］。因此，国内外学者将超精密磨削技术应用于硬脆材料基片的高质量加工。目前，超精密磨削已广泛应用在单晶Si、单晶SiC 等硬脆晶体基片的高质量加工中［13-16］，其加工效率远高于研磨，且工件旋转法磨削工件的面形精度容易控制，通过采用细粒度的砂轮和优化磨削参数还能够使磨削表面以塑性域方式去除材料，获得低损伤表面，进而减小抛光的损伤去除余量，提高基片的抛光效率［14-15］。

为了实现YAG 晶体的低损伤磨削加工，很多学者对YAG 晶体的超精密磨削工艺进行了系统的研究。研究结果表明，通过控制磨削加工的砂轮粒度，降低磨粒切深，可以使YAG 磨削表面由裂纹、破碎坑共存的“脆塑共存表面”转变为“塑性磨削表面”。塑性磨削表面无任何脆性损伤、剥落，只有塑性磨削痕迹，具有较高的表面质量［17-18］。因此，研究YAG 晶体超精密磨削中的脆塑转变深度，对于实现YAG 无脆性损伤的“塑性域”加工具有重要意义。现有研究主要围绕硬脆材料加工过程中表面的材料去除方式展开。Bifano 等［19］通过开展大量工程陶瓷和光学玻璃等硬脆材料的塑性域磨削试验，首次提出硬脆材料“塑性域”加工的概念，并基于压痕断裂力学建立临界深度与硬脆材料力学性能的数学关系模型，结合大量试验结果确定了模型中的比例系数，首次建立了硬脆材料脆塑转变临界深度的预测模型。Huang 等［20］同样开展磨削试验，详细地分析Bifano 建立的模型并进行修正，提高了模型预测精度。Arif 等［21］假设脆性材料加工中材料去除模式的转变伴随着能量消耗模式的相应转变，基于比切削能从塑性变形模式转变为断裂模式的变化，建立了脆性材料脆塑过渡预测模型。Venkatachalam 等［22］认为应力强度因子等于材料断裂韧性时即为脆塑变形过渡点，基于约翰逊库克材料模型并采用Irwin 应力强度因子计算模型，建立了临界切削厚度预测模型。李琛［17］和李洪刚［23］等基于弹塑性接触理论，详细分析了单颗金刚石压头划擦作用下硬脆材料表面的变形过程，分别建立了脆塑转变临界深度预测模型。然而，现有的脆塑转变临界深度预测模型中，各项材料力学性能都以测得稳定值代入计算，忽略了磨粒与材料不同深度接触区域的材料力学性能差异。大量研究表明，微观尺度下YAG 等硬脆材料的硬度、弹性回复率等力学性能随压痕深度的改变会发生明显变化［24-26］，人们认为硬脆材料的微观力学性能具有明显的尺寸效应［27-28］。这导致目前的理论研究结果与实验结果仍存在一定误差。

本文基于弹塑性接触理论和压痕断裂力学，通过分析单磨粒划擦作用下材料表面的变形过程，考虑材料的弹性回复、微观下力学性能的尺寸效应，建立脆塑转变临界深度预测模型，通过纳米压、划痕试验测得YAG 晶体的微观力学性能代入预测模型，计算YAG 晶体超精密磨削的脆塑转变临界深度，并通过不同粒度金刚石砂轮超精密磨削YAG 晶体试验验证了模型的可靠性。

2 试 验

试验材料为透明的YAG 晶体，样件尺寸为10 mm×10 mm，厚1 mm，已抛光预处理使初始表面粗糙度Sa都处于0.5 nm 以内，如图1 所示。

图1 试验样品Fig.1 Test samples

2.1 纳米压痕试验

纳米压痕试验采用美国KLA 公司的Nano Indenter G200，如图2（a）所示。采用的金刚石压头为标准Berkovich（玻氏）压头，尖端半径R≈20 nm，如图2（b）所示。压痕试验参数如表1所示。

表1 纳米压痕试验参数Tab.1 Nano-indentation test parameters

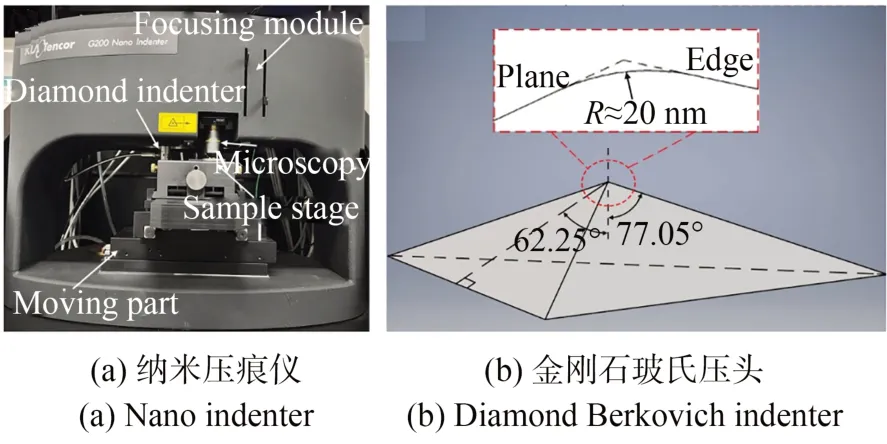
图2 试验设备Fig.2 Experimental equipment

2.2 准静态纳米划痕试验

纳米划痕试验采用美国KLA 公司的Nano Indenter G200，如图2（a）所示。有研 究 表 明，划痕速率的提高会使硬脆材料表面的变形情况发生极大变化［29-30］。为避免应变率效应的影响，玻氏压头选择低划痕速率以棱朝前模式进行准静态下的试验，试验参数如表2 所示，线性加载划痕过程如图3 所示。 使用JSM-7610FPlus 场发射扫描电镜（JEOL，日本）观察划痕表面。

表2 准静态纳米划痕试验参数Tab.2 Quasi-static nano-scratch test parameters

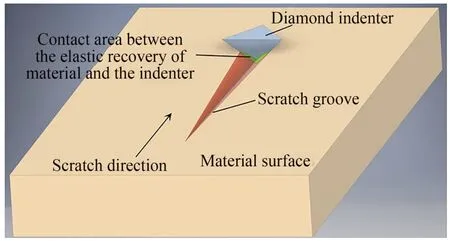
图3 棱朝前线性加载纳米划痕示意图Fig.3 Schematic diagram of linear loading nano-scratche with edge forward

2.3 超精密磨削试验

图4 所示为VG401MKII 超精密磨床（OKAMOTO，日本），主轴配有高精度空气轴承，轴向跳动和径向跳动可限制在0.05 μm 以内。磨床的轴向刚度为1 176 N/μm，径向刚度为205.8 N/μm。该机床采用工件旋转法磨削方式。YAG 晶体用石蜡固定在硅片上距中心35 mm处，硅片通过真空吸盘吸附在工作台上，并使中心重合。杯型砂轮直径为350 mm，磨削层通过工作台中心，磨削时砂轮和工件分别绕各自轴线旋转，同时砂轮沿轴向进给实现材料去除，冷却液采用去离子水。磨削试验参数如表3 所示，为完全消除前道工艺产生的表面/亚表面损伤对试验结果的影响，在磨削试验中的材料去除厚度确定为50 μm。使用JSM-7610FPlus 场发射扫描电镜、NewView9000 型3D 表面轮廓仪（ZYGO，美国）观察磨削后YAG 晶体表面的粗糙度和形貌。

表3 工件旋转法超精密磨削试验参数Tab.3 Parameters of workpiece rotation ultra-precision grinding tests

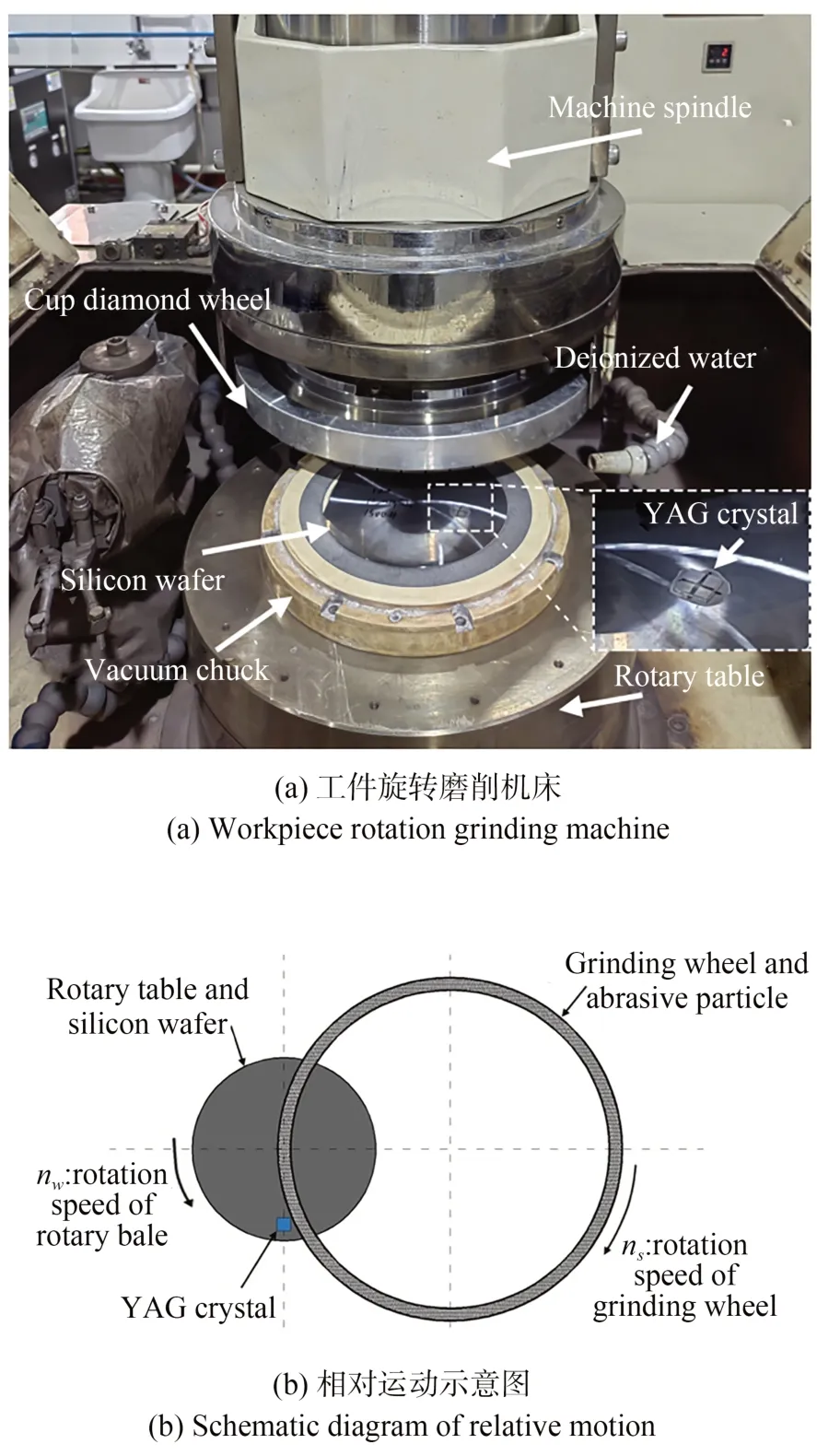
图4 超精密磨削设备及方法Fig.4 Ultra-precision grinding equipment and method

3 试验结果

3.1 纳米压痕试验结果

如图5 所示，随着法向施加载荷的减小，对应卸载曲线最高点处的斜率逐渐变小，同时整体变形中弹性变形量占比有所增大。首先，基于Oliver-pharr 分析法计算得到接触刚度，进而获得YAG 的力学性能［31］。试验结果表明，载荷较小时，计算获得的弹性模量、微纳米硬度以及弹性回复率越高；随着载荷的逐渐增大，材料的力学性能降低并趋于稳定，具有明显的尺寸效应，如图6 所示。随载荷的增大，弹性回复率也由70.5%降低趋近稳定值35.2%。YAG 晶体的弹性模量E、微纳米硬度H分别稳定在325 GPa 和20 GPa。

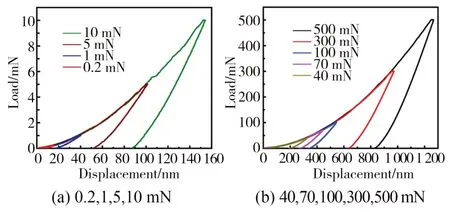
图5 纳米压痕载荷深度曲线Fig.5 Load depth curves of nano-indentation

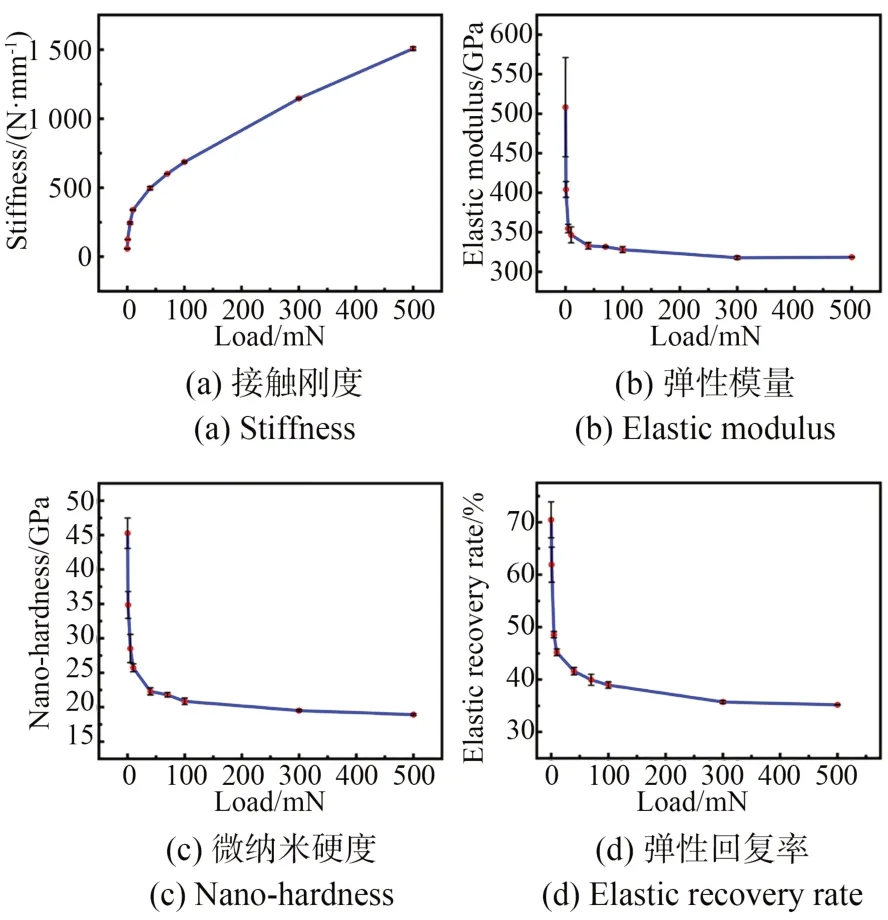
图6 YAG 微观力学性能Fig.6 Micro-mechanical properties of YAG

3.2 准静态纳米划痕试验结果

划痕表面如图7 所示，在距初始端5.5 μm 处首次观察到沟槽内裂纹这一脆性变形特征，视此处为脆塑转变临界位置。因为线性加载模式中载荷（由0 mN 逐步增大到100 mN）与划痕位移（从初始位置到100 μm 处）相对应，可确定该位置对应的载荷为无裂纹产生的临界载荷，即P*=5.5 mN。

图7 YAG 准静态划痕沟槽的表面形貌Fig.7 Surface morphology of YAG quasi-static scratch groove

3.3 超精密磨削试验结果

超精密磨削试验后YAG 晶体表面的形貌及粗糙度分别如图8 和图9 所示。对比不同砂轮磨削试验的加工表面，可以观察到#325，#600 砂轮磨削表面存在破碎坑、裂纹等损伤，#325 砂轮磨削表面的破碎坑尺寸更显著且表面粗糙度Sa接近微米级。由此表明，#325，#600 砂轮磨削加工时，晶体表面材料的去除方式以脆性断裂为主。#1 500，#3 000 砂轮磨削表面则大幅改善，磨粒划擦过的磨削纹路规则排列，表面没有发现破碎坑、裂纹等脆性损伤。#3 000 砂轮磨削表面的细微磨纹更为平整，表面粗糙度Sa接近1 nm。#1 500，#3 000 砂轮磨削以塑性流动方式去除晶片表面材料。

图8 磨削试验样件的表面形貌Fig.8 Surface morphology of grinding test samples

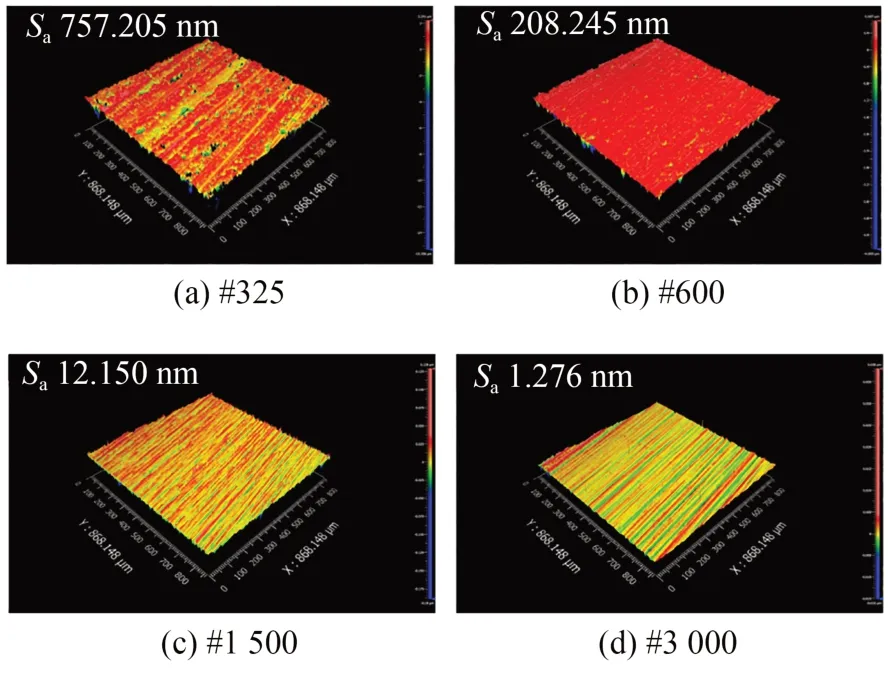
图9 磨削试验样件的表面粗糙度Fig.9 Surface roughness of grinding test samples

4 讨 论

磨削加工硬脆材料时，控制磨粒切深低于脆塑转变临界深度，可实现“塑性域”加工，获得低损伤表面。准确的脆塑转变临界深度预测模型能为硬脆材料的低损伤加工提供理论指导。因此，本文基于分析单磨粒准静态划痕过程中表面材料变形情况，考虑材料的弹性回复及其尺寸效应，建立脆塑转变临界深度预测模型。

划痕过程中，压头与材料的实际接触投影面积与压头法向载荷以及划痕硬度的关系如下：

其中：HS为材料硬度，FN为压头法向载荷，AN为压头与材料的接触投影面积。

如图10 所示，玻氏压头与材料的实际接触投影面积与划痕深度呈几何关系。划痕过程中，实际接触投影面积要考虑两部分：AN1蓝色区域为压头划动朝前一端与材料划擦推挤的接触投影面积；AN2黄色区域为压头划过后表面材料弹性回复的接触投影面积。AN1与压头形状和切深呈几何关系，具体为：

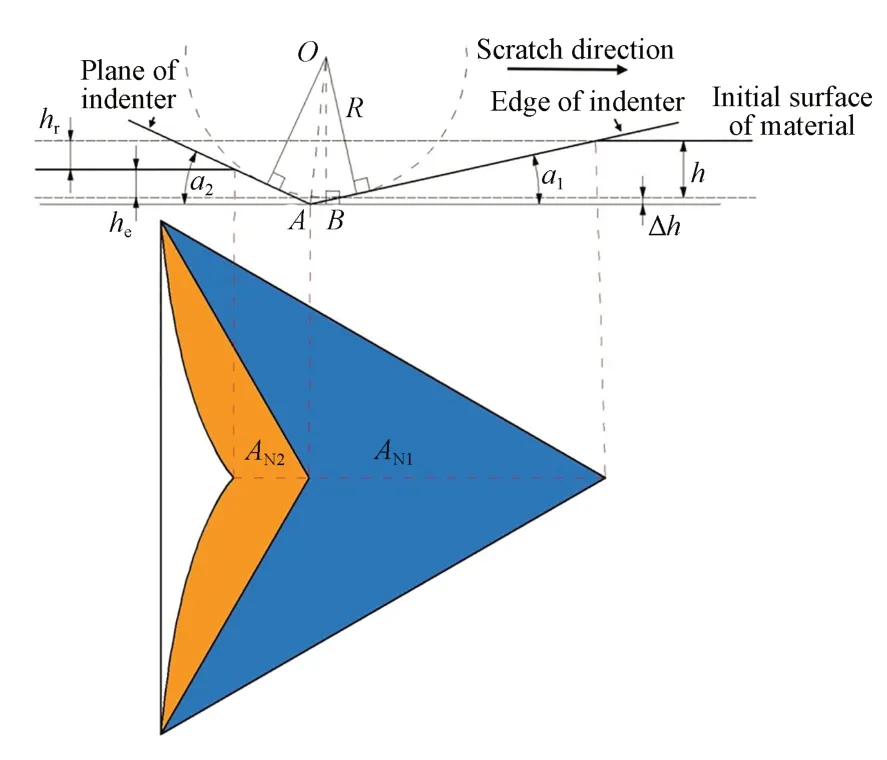
图10 划痕过程中玻氏压头与材料的实际接触投影面积Fig.10 Projection of actual contact area between Berkovich indenter and material during scratch

其中Δh为理想划痕深度与实际划痕之差，由式（3）计算：

其中：h为压头划痕深度，hr为残余深度；a1=12.95°和a2=24.75°，分别为玻氏压头的棱边和面与水平线之间的夹角；R为所采用的玻氏压头的尖端半径，为20 nm。计算得到Δh=1.025 nm。

因为AN2为材料弹性回复后与压头后端接触区域的投影面积，其计算要考虑到弹性回复率。许多学者在硬脆材料上发现压痕压入深度越小，弹性变形的占比越大，弹性回复率越高［24-26］。所以，本文根据过往研究推导出弹性回复率与压入深度之间具体的函数关系，并用压痕试验结果拟合出曲线。

由纳米压痕中硬度的定义可知，法向载荷P与接触投影面积A成正比，而接触投影面积A与深度h0的关系为［31］：

式中：C0为常数，对于玻氏压头C0为24.5。

在载荷深度曲线的加载过程中，法向载荷与压入深度的平方成正比。在载荷最大为FN时，深度同为最大值hmax，即有［32］：

其中C为与材料种类相关的常数。整理式（5）得到：

在压痕试验分析材料特性常用的Oliverpharr 分析法中，载荷位移曲线的卸载部分可表示为［31］：

其中：a与m为拟合参数，hr为残余深度，P，h分别为卸载时的载荷和对应深度。在卸载过程中，载荷最大时，深度为hmax，卸载的弹性回复量he=hmax-hr，代入式（7）得到：

将式（6）与式（8）代入弹性回复率的定义式可推导出弹性回复率与压入深度的关系如下：

因C，a，m都为拟合参数，令，得弹性回复率与深度成幂函数关系，即：

应用纳米压痕试验测得数据对式（10）进行拟合，hˉ用于消除量纲，为1 nm。

使用压痕测得各载荷下的弹性回复率数据用 于 式（10）的 拟 合，得 到A为110.74，B为-0.168，拟合优度R2＞0.95，如图11 所示。

图11 弹性回复率尺寸效应的拟合曲线Fig.11 Fitting curve of elastic recovery size effect

对式（10）从两侧划痕边缘到中部（划痕深度为h）进行积分计算，可得弹性回复接触投影面积：

划痕过程中实际接触投影面积为：

代入式（1），可得到划痕深度h与法向载荷FN的关系：

其中划痕深度h随法向载荷FN单调递增，所以式（13）中明确临界载荷可求得对应的深度ḣ。

表面形变过程中，在形变区域边缘存在压入深度极低只发生弹塑性变形的情况，此时压头接触深度h始终小于实际最大压痕深度hmax，如图12 所示。两者关系如下［31］：

图12 表面变形形貌截面示意图Fig.12 Schematic diagram of cross section of surface deformation morphology

其中：ε为压头形状的影响系数，对于玻氏压头为0.75，FN为法向载荷，S为对应法向载荷时的接触刚度，在压痕试验测得接触刚度数据中插值取得。

准静态划痕试验与压痕试验的材料变形过程均匀缓慢，避免了应变率的影响，所以脆塑性临界深度预测模型也应考虑式（14）的情况，那么划痕时在脆塑转变临界位置有：

式中：P*为法向载荷，接触刚度S为164 N/mm。

Lawn 等基于压痕断裂力学得出材料发生脆塑性转变时的临界载荷公式为［33］：

其中：λ0为材料的无量纲修正系数，KC为断裂韧性，取2.2 MPa·m12［34］。代 入 准 静 态 划 痕 试 验 观察的脆塑转变临界载荷值5.5 mN，求出YAG 晶体的λ0为1 878.28。

联立式（13）、式（15）和式（16）可得最终脆塑转变临界切深预测模型：

其中h*为预测硬脆材料的临界切深。

将纳米压、划痕试验中获得相关力学参数与各项系数代入式（17）和式（18），计算出预测脆塑转变临界深度h*为66.7 nm。

目前，学界普遍认为材料力学性能是影响硬脆材料的脆塑转变临界深度的关键因素，而磨削速度则影响的是磨粒的实际切深［19-21］。由准静态纳米压、划痕试验测得的微观力学性能最终计算出的临界深度h*，可由更高划擦速度的磨削试验进行验证。

用Zhang 等［35］建立的工件自旋转法磨粒切削深度解析模型来计算实际的磨粒切深：

其中：rg为磨粒的 平均半径，f为进给 率，R1是工件距离工作台旋转中心的径向距离为35 mm，nw，ns分别为工作台和砂轮的转速，θ是磨粒切削角为38°，η为砂轮的磨粒体积比取0.25，k为砂轮有效磨粒比取0.15，W是磨齿宽度为3 mm，D是砂轮直径为350 mm，H为加工工件硬度，Et⋆为砂轮结合剂的杨氏模量（树脂与陶瓷结合剂分别为40 GPa 和80 GPa）。

由 式（19）计 算 得 到#325，#600，#1 500，#3 000 砂轮磨削试验中磨粒的切削深度分别为160.7，83.7，33，16.7 nm，与脆塑转变临界深度h*进行对比，结果如图13 所示。由图13 可知，#325，#600 砂轮的磨粒切深高于脆塑转变临界深度h*，磨削加工时表面材料的去除方式主要为脆性去除，加工表面质量较差，出现大量显著的破碎 坑、裂 纹 等 表 面 损 伤，与 图8（a），8（b）和图9（a），8（b）中#325，#600 砂轮的磨削结果相符。Bifano 首先提出了“塑性域”磨削概念，并把工件表面可观测的脆性断裂区域少于10%作为判定“塑性域”去除模式的指标［19］。人们将磨削表面形貌无破碎、凹坑等损伤或表面呈现塑性变形特征作为依据来判断是否为“塑性域”磨削［36-38］。#1 500，#3 000 砂轮磨削试验的磨粒切深低于脆塑转变临界深度h*，磨削加工时表面材料以塑性流动方式去除，可实现“塑性域”加工，获得低损伤、高质量的加工表面，与图8（c），8（d）和图9（c），9（d）中#1 500，#3 000 砂轮的磨削结果相符。

图13 磨粒切削深度示意图Fig.13 Schematic diagram of abrasive cutting depth

5 结 论

本文开展YAG 晶体在不同载荷下的纳米压痕试验，检测其微观力学性能弹性模量E、微纳米硬度H和弹性回复率。随载荷增大，弹性模量E、微纳米硬度H各趋近稳定值325 GPa 和20 GPa，弹性回复率由70.5%降至35.2%，具有尺寸效应。开展准静态线性加载纳米划痕试验，测得YAG 晶体表面的无裂纹产生的临界载荷为5.5 mN。通过分析单磨粒划擦下YAG 晶体材料表面的微观变形过程，基于弹塑性接触理论和压痕断裂力学，考虑材料的弹性回复、微观下力学性能的尺寸效应，建立了脆塑转变临界深度的预测模型。结合YAG 晶体的微观力学性能及无裂纹产生的临界载荷，计算得到YAG 晶体的脆塑转变临界深度为66.7 nm。采用不同粒度砂轮开展磨削试验对预测模型进行验证，并计算不同粒度砂轮在相同工艺条件下的磨粒切深。结果表明，#325，#600 砂轮磨粒切深高于YAG 晶体脆塑转变临界深度，以脆性方式去除表面材料，加工表面有大量显著的破碎坑、裂纹等损伤；#1 500，#3 000 砂轮磨粒切深低于预测脆塑转变临界深度，以塑性方式去除表面材料，加工表面无脆性去除的损伤，粗糙度Sa达到1 nm，实现了“塑性域”加工。本文建立的硬脆材料脆塑转变临界切深预测模型，能够较好地解释YAG 晶体超精密磨削过程中的材料去除机理，从而指导YAG 晶体的低损伤磨削加工，获得高质量表面。