集成视觉显著性和群决策的航空零件孔特征检测

田佳淳， 王 亮， 梅 标， 朱伟东

（1.浙江大学 工程师学院，浙江 杭州 310015；2.中航西安飞机工业集团股份有限公司，陕西 西安 710089；3.中国科学院 福建物质结构研究所 泉州装备制造研究中心，福建 泉州 362100；4.浙江大学 机械工程学院，浙江 杭州 310058）

1 引 言

孔特征检测是航空零件质量评估和航空结构件自动化精准制孔的重要环节。航空钣金件自动化检测时，孔特征检测是计算孔边距、孔间距等几何尺寸的基础；航空结构件自动化制孔时，基准孔检测用于引导自动化制孔系统实现制孔位置修正［1］。传统的人工检测方法存在误差大、复现性差、劳动强度大，难以适应数字化装配制造需求等缺点。随着机器视觉相关理论和技术的不断发展，视觉测量技术凭借其非接触、自动化等特点，在测量领域得到了广泛的应用［2］。不过，在复杂工业生产环境中实现高效高精度的孔特征视觉检测对所采用的检测算法提出了更高要求。

目前，研究人员提出了多种航空零件孔检测算法。张太恒等［3］提出了检测复合材料圆孔的VGSR 算法，将纹理边界引导和随机圆检测相结合实现多孔检测，但该算法只适用于纹理边界与圆边界相吻合的场景。Yu 等［4］结合边缘跟踪和RANSAC 拟合算法实现了飞机壁板上的埋头孔检测，该算法在划痕、毛刺、污渍下的抗噪性能较好，平均检测时间在0.5 s 左右，时间成本较高。Lou 等［5］结 合SURF 和DBSCAN 算 法 对 飞 机 蒙皮上的遮挡基准孔进行区域分割，并利用Kmeans 聚类和椭圆几何性质提取孔轮廓，最后基于最小二乘拟合轮廓。该方法具有不同光照条件下的检测稳定性，但定位精度在0.03 mm 左右，测量精度并不高。

孔轮廓提取与拟合是孔检测算法的关键组成，直接影响孔的视觉检测精度。孔轮廓提取是从图像中自动或半自动地识别和提取孔的轮廓信息，边缘检测则是其中的重要技术之一。常用的边缘检测算法包括一阶微分算子如Sobel，Roberts，以及二阶微分算子如LoG，Canny 等［6］。数学形态学是在格论和拓扑学上利用不同结构元素对图像进行形态学运算，以此获得图像边缘［7］。孔轮廓拟合则是基于统计分析和特定数学模型如圆、椭圆等拟合轮廓数据，从而确定最佳匹配的形状参数。

在提取孔轮廓时，通常希望孔与背景具有高对比度，孔边缘清晰。视觉显著性源于视觉注意力模型，旨在识别图像中最具吸引力和显著性的区域，准确地从复杂图像中突出显著特征［8］。显著性检测通过定位图像中最显著的区域，可以帮助人们更快速地理解图像的内容，从而提高图像处理和分析的效率。经典方法包括谱残差（Spectral Residual， SR）方法［9］、频率调谐（Frequency Tuned， FT）方法［10］和基于图的流行排序（Manifold Ranking， MR）方法［11］等。此外，还有基于深度学习的方法。Yang 等［12］提出了一种端到端扩张初始网络DINet，将显著性预测转变为全局概率分布预测任务。王向军等［13］提出了一种主干模型为嵌套U 型网络的EGMFNet，并在较低层级引入由边缘信息引导的全局空间注意力模块。若将视觉显著性算法用于实际航空制造这一特殊工业场景，本文认为其应满足以下要求：（1） 算法应生成全分辨率显著图，且显著特征应突出并具备清晰的边界；（2） 算法应在恶劣的工业场景下保持较高的稳定性，且能实现高效的检测。经典的FT 方法可以高效地生成全分辨率显著图，但生成的显著图中孔特征不够突出，因此亟需进行改进。

在拟合孔轮廓时，需充分考虑离群点的影响［14］。Meanshift 算法通过迭代寻找数据分布的最大密度区域，因此在计算核平均位置时，离群点对核移动的幅度影响较小。Cheng 等［15］通过引入核函数和权重系数进一步扩大了算法的使用范围，使它广泛应用于聚类［16］、图像分割［17］及目标跟踪［18］等场景中。群决策是管理领域的概念［19］，其含义是最佳决策的制定需要集中群体优势和众人智慧，该思想对于圆拟合算法设计具有一定的启发意义。

受实际航空制造场景中不均匀光照、噪声、污渍和孔内壁干扰等的影响，孔特征检测需要一种稳定性更强的算法。为了提高孔检测的抗噪性能，弱化外部环境因素的影响，同时获得较高的检测精度和效率，本文提出了一种适用于航空制造场景的孔特征检测方法，用于实现含孔航空钣金件尺寸特征的精确检测与航空零件制孔中基准孔的精确定位。

2 算法原理

2.1 改进的FT 显著性特征检测

FT 方法是一种基于空间频域分析的显著性检测算法，通过比较像素颜色与图像平均颜色之间的差异来估计像素的显著性。该算法流程如下：首先对输入图像进行高斯平滑处理，然后将颜色空间从RGB 转换到LAB，LAB 与RGB 颜色空间不同，它分离了亮度信息即L 通道和颜色信息即A 通道和B 通道，然后在LAB 中计算平滑后图像的各个颜色通道的均值，最后根据式（1）计算显著值。

式中：Iμ（x，y）为图像在LAB 颜色空间中的像素算术平均值，Iωhc（x，y）为图像的高斯模糊模板，‖ ‖指计算欧式距离。

在计算过程中，像素的显著值越大，属于显著区域的可能性就越大，在显著图中被高亮显示。图1 为原始孔图像以及经典FT 方法的检测结果，平均处理时间为0.12 s。图1（b）表明，尽管该算法检测速度较快且输出全分辨率的显著图，但显著区域即孔所在区域的像素被抑制，并且受到背景中划痕、毛刺等干扰，孔特征不够突出，不利于孔区域的提取。

图1 原始孔图像以及经典FT 方法的检测结果Fig.1 Original hole images and detection result of classical FT method

本文对经典的FT 方法进行改进。由于在FT 方法中显著值与像素颜色和图像平均颜色之间的差异密切相关，所以增强图像各像素间的差异有利于突出显著特征。在平滑输入图像和转换颜色空间两个步骤之间，增加图像增强步骤，具体方法如下：

式中：Ires为增强后的灰度值，round（）为四舍五入取整函数，Iori为原始灰度值，Iave为原始灰度平均值，Imax为原始最大灰度值，Imin为原始最小灰度值，E为增强因子。E过大，会导致图像出现伪影并引入过多噪声；E过小，会导致图像边缘模糊和细节丢失，可根据实验测试结果进行设置。为便于后续图像处理，这里根据图像背景的复杂程度将E设为［3，10］，图像背景越复杂，增强因子越大。

该方法引入增强因子使得增强程度可调，调整图像灰度值时兼顾灰度平均值、最大、最小灰度值等图像原有特征，以便使得图像中原本亮的区域更亮、暗的区域更暗，从而在后续显著值计算中获得更大的数值差异。

在基于式（2）～式（4）对FT 方法进行初步改进后，对图1（a）中的原始图像进行显著性检测，如图2 所示。结果表明，得到的显著图中孔特征更加突出，被高亮表示；但图中混入较多不属于孔区域的干扰项，因此有必要进一步滤除背景中孤立的碎片化显著区域。

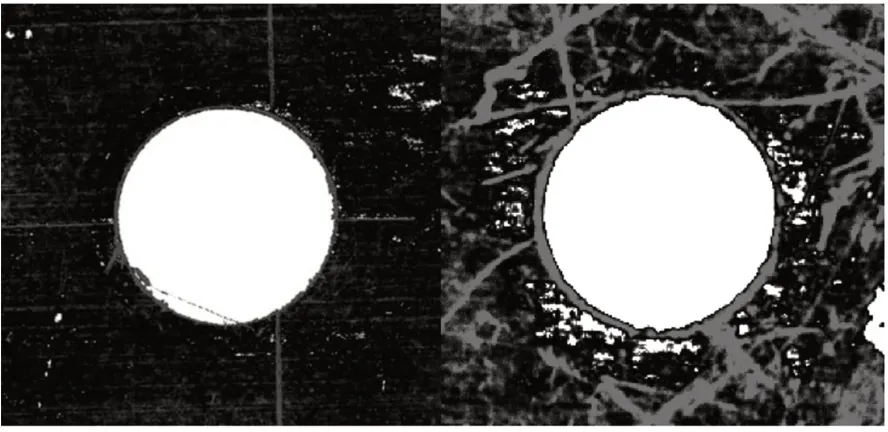
图2 基于初步改进FT 方法的显著性检测结果Fig.2 Saliency detection results based on preliminary improved FT method

显著图中面积最大的显著区域通常作为显著区域定位和估计结果。利用区域筛选算子，根据“最大面积”特征，提取面积最大的显著区域，并根据每个像素到最大显著区域中心的距离预测显著目标。这里认为靠近最大显著区域中心的部分属于最终显著区域，而远离最大显著区域中心的部分则属于背景。根据式（5）～式（7）生成以最大显著区域中心为参考的权重分布。权重分布从1 到0，中心权重值为1，边缘权重值趋近于0，从区域中心到边缘权重逐渐减小，将这些权重赋给先前步骤中计算得到的显著值得到最终显著值。

式中：h为生成的权重，dp为像素到最大显著区域中心的距离，Rw为根据最大显著区域特征设定的权重半径，floor（）为向下取整函数，sqrt（）为平方根函数，S为最大显著区域面积，π 为圆周率，Rp，Cp为图中任意位置像素的横纵坐标，Xc，Yc为最大显著区域的中心坐标。

在对FT 方法进行最终改进后，对图1（a）中的原始图像进行显著性检测，结果如图3 所示。与图1（b）相比，在基于改进FT 方法获得的全分辨率显著图中，孔特征更加突出，并且边界清晰。图像背景中划痕、毛刺等干扰显著减少，有利于后续的阈值分割。由于该算法已将显著值归一化到［0，255］，因此，只需设定适当的阈值就可以从显著图中分割出孔区域。经过多次实验测试，灰度阈值设为47 即可从显著图中分割出孔区域。

图3 基于最终改进FT 方法的显著性检测结果Fig.3 Saliency detection results based on final improved FT method

2.2 新型数学形态学轮廓提取

数学形态学利用结构元素对图像进行形态学运算，从而实现图像的分析和识别，具有计算复杂度小、对图像几何特征不敏感等特点。其基本运算有膨胀和腐蚀，其余运算是这两种基本运算的复合，如开运算、闭运算等。

基本的数学形态学算子操作简单快速，但去噪效果不佳，在实际图像边缘提取中难以运用。因此研究人员构造出复合算子［20］，如下：

式中：A为灰度图像，B为结构元素，∘为开运算，·为闭运算，Θ 为腐蚀运算，⊕为膨胀运算，-为差运算。

经过测试，基于上述算子处理显著图时均不能有效抑制噪声，会导致孔轮廓误检。图4 为基于式（8）表征的算子对显著图的孔轮廓检测结果，其中结构元素B设置为常用的3×3 像素的矩形，红色区域为检测到的孔轮廓（彩图见期刊电子版）。由于先前步骤得到的显著区域存在部分孔轮廓缺失、孔内部区域有空洞等问题，该方法不加区分地将这些缺陷处的轮廓均视为孔轮廓，如图4 中白框区域所示，这会导致后续轮廓拟合引入较多的误差。

图4 基于现有算子的孔轮廓检测Fig.4 Hole contour detection based on existing operator

为了获取更多真正的孔边缘信息，同时去除冗余轮廓，本文设计了一种新的孔轮廓提取算法，主要包括基于多尺度多结构元素的新型形态学边缘检测算法以及轮廓细化算法。在新型形态学边缘检测算法中，设计了新型形态学边缘检测算子，如下：

式中：A为灰度图像，B1，B2，B3均为结构元素，∘为开运算，·为闭运算，Θ 为腐蚀运算，⊕为膨胀运算，-为差运算，∩为交运算，∪为并运算。

在基于数学形态学的轮廓提取中，结构元素的选择很重要。在基于式（8）和式（9）这类具有单个结构元素形态学算子进行边缘检测时，选用大尺寸结构元素能有效去除噪声，但处理后的图像边缘细节信息不突出；选用小尺寸结构元素能较好地保护边缘细节，但去噪声效果不佳。此外，检测对象圆孔为非线性结构，因此算法中的结构元素应设计为非线性结构。B1，B2，B3为设计的不同结构元素，如下：

其中B3为具有自适应大小的圆结构元素，其半径r与1.1 节中得到的显著区域面积相关，B3（r=2）表示r等于2 个像素时的B3。

运用上述新型数学形态学边缘检测算子对图3 中左侧显著图进行检测，结果表明，该方法在保留轮廓关键信息的同时，可以有效简化孔轮廓，检测到的轮廓点数量为817 个，而基于式（8）算子检测到的轮廓点数量高达1 186 个。研究发现，虽然提出的新边缘检测算子已经简化了孔轮廓，但仍然包含部分尺寸超过1 个像素的区域，导致后续轮廓拟合时存在信息冗余。骨架是基于物体对象形状特征的简化描述方式，是指图像的中央线条部分［21］。可利用骨架提取算子对得到的孔轮廓进行细化处理，结果表明，细化后的轮廓点数量仅为710 个。

图5 为采用新型数学形态学轮廓提取算法提取的显著图的孔轮廓。结果表明，该方法能有效过滤缺失区域轮廓以及区域内部空洞轮廓等噪声，减少后续轮廓拟合时的计算误差，从而在提取孔特征轮廓关键信息的同时，降低轮廓点数量，有利于提高后续轮廓的拟合精度和效率，确保航空钣金件的检测精度和航空结构件基准孔的定位精度。

图5 新型数学形态学轮廓提取方法的检测结果Fig.5 Detection results of novel mathematical morphological contour extraction method

2.3 融合Meanshift 和群决策的轮廓拟合

基于2.2 节得到的轮廓点仍有可能包含由毛刺、污渍、灰尘等缺陷引入的离群点，直接对所有轮廓点进行最小二乘拟合，会引入较多误差。因此，本文提出了一种融合Meanshift 和群决策的圆检测算法，该算法主要包括圆心位置寻找和半径计算两个部分。

首先计算每个轮廓点的坐标，并将所有点坐标按照轮廓顺序保存在一个数组中。设置分段点数Tc，其值为轮廓点总数与3 相除得到的商并向下取整，按照下标将轮廓点数组分成［0，Tc-1］，［Tc，2Tc-1］和［2Tc，3Tc-1］三组，从每组中随机选取一个点，使用最小二乘法拟合圆，并将拟合后的圆心和半径保存在另外两个数组中。

分段拟合结果显示，少数圆心分散在各个位置，而大多数圆心集中在一个区域，可以认为真正的圆心就在该区域中。结合Meanshift 算法可以使目标收敛到点群密度最大处，因而制定如下的圆心位置寻找步骤：

（1）从分段三点拟合得到的圆心点群中任选一点作为初始质心，位置记为（Xo，Yo），并以初始质心为中心按照预先设置的扫描半径进行扫描；

（2）基于Meanshift 算法，寻找该扫描范围内圆心点群的新质心，其位置记为（Xr，Yr）；

（3）基于新旧质心坐标计算它们之间的欧式距离，记为误差Te，如果Te大于预设值Ts，则继续重复执行步骤（1）和（2），其中上一次的质心成为下一次的扫描中心；

（4）循环结束后，选取最后一次的质心位置作为最终的圆心位置，并统计在扫描半径范围内的所有圆心点及其对应的拟合半径。

图6 为圆心点群和基于Meanshift 的质心迭代过程。图中，圆点表示通过分段三点拟合得到的圆心，十字表示质心，红色箭头为初始质心到最终质心的迭代方向，初始质心经过多次迭代收敛到圆心点群密度最大处。黑色箭头所指的图像是经过基于Meanshift 质心迭代后的孔圆心位置（彩图见期刊电子版）。

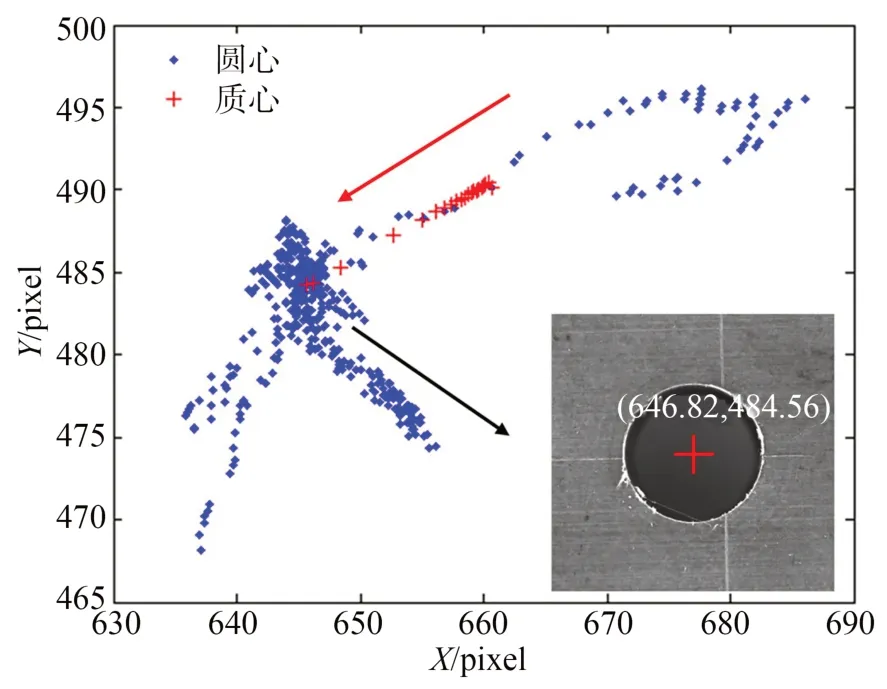
图6 基于Meanshift 的质心迭代过程Fig.6 Process of centroid iteration based on Meanshift

根据群决策理论，同一组员对不同问题、不同组员对同一问题的意见大多不同，基于某个组员的威望、知识水平等先验因素得出结论过于主观随意，而兼顾每个组员的意见也未必正确，因为这需要提前确认所有组员的意见都合理。本文借鉴群决策的思想，设计了一个用于半径计算的群决策模型。假设有n位组员参与某个有m类问题的工程决策，则意见矩阵如下：

式中dij为第j个组员对第i类问题的意见。意见用介于0 和1 间的数字表示，数字越大表示越重视。矩阵每行表示不同组员对同一问题的意见，每列表示同一组员对不同问题的意见，且每列各个意见的总和为1。

由于确定某类问题的最终意见要兼顾每位组员的合理意见，充分利用组员们的群体智慧，所以模型的最终目标函数用最终意见与每位组员意见的最小偏差来表示，如式（14）所示：

式中：dij为第j个组员 对 第i类问题的 意 见，di为对第i类问题的最终意见。最终意见需要满足：

在计算半径时，首先筛选扫描半径范围内的所有圆心点及其对应的拟合半径。设置阈值Tv=1。计算各圆心点与最终圆心间的距离，若距离小于阈值Tv，则该圆心点及其对应的拟合半径被视为第i类问题。计算各圆心点与最终圆心间的距离与所有距离总和的比值，视为1 号组员对每类问题的合理意见。计算各拟合半径与所有半径总和的比值，视为2 号组员对每类问题的合理意见。基于群决策模型计算上述各类问题对应的最终意见，计算最终半径得到：

式中：ri为第i类问题对应的半径，di为第i类问题的最终意见，r为最终半径。

完整轮廓拟合算法的伪代码如表1 所示。

表1 算法的伪代码Tab.1 Pseudocode of algorithm

3 实 验

为验证所提出的孔特征检测算法的可靠性和有效性，基于工业相机在不同环境下对不同零件上的孔进行拍摄，得到孔特征检测图像。其中，一部分检测图像为图7 所示的钣金件视觉检测实验平台拍摄的实验件，另一部分检测图像为图8 所示机器人制孔系统上集成的视觉系统拍摄的孔图像。其中，钣金件视觉检测实验平台由相机支架、工业相机、镜头、环形光源、试验件和计算 机 组 成。 计 算 机 处 理 器 为Intel（R） Core（TM） i7-7700HQ CPU @ 2.80 GHz，使用Visual Studio 2019 软件和Halcon 机器视觉库进行联合编程。通过相机标定获得当前条件下的像素当量约为0.025 mm/pixel。

图7 钣金件视觉检测实验平台Fig.7 Visual detection test platform for sheet metal parts

图8 航空结构件机器人制孔系统Fig.8 Robotic drilling system for aircraft structural parts

3.1 稳定性实验

在实际航空制造场景中，常常遇到许多复杂情况，导致获取的图像无法清晰和完整显示孔特征。为了验证提出的孔特征检测算法的稳定性，对在不均匀光照、孔缺陷、孔内壁干扰等情况下拍摄的基准孔和钣金件孔图像进行检测。

检测结果如图9 所示，在光照不均匀导致部分孔轮廓特征缺失或者孔轮廓不突出，以及孔轮廓存在毛刺和污渍等缺陷的情况下，提出的算法仍能获得良好的检测结果。

图9 存在不均匀光照和孔缺陷时孔特征检测结果Fig.9 Hole feature detection results under uneven lighting and hole defects

由于改进的FT 算法在检测过程中采用高斯滤波，所以在抗噪性实验中主要针对椒盐噪声进行测试。制作的孔检测图像如图10 所示，图像尺寸为660×640 像素，包括毛刺、缺损等孔缺陷，以尽可能模拟实际航空制造场景下的复杂孔缺陷。

图10 人工制作的孔图像Fig.10 Artificially created hole image

抗噪性能检测中，通过在图像中添加不同密度的椒盐噪声后比较孔检测结果，椒盐噪声密度指的是噪声所占当前图像全部像素的百分比。在人工制作的孔图像中分别添加了5%，10%，15%，20%，25%，30%密度的椒盐噪声，并使用提出的算法进行检测。

图11 为抗噪性实验结果，其中纵坐标定义为孔内实际检测结果与理论参数之间的差异。结果显示，在不同的椒盐噪声密度下，采用提出的算法进行圆心坐标（X，Y）和半径R检测的误差均在0.012 mm 以下。即使在椒盐噪声密度高达30%的情况下，仍能完成孔特征检测，这表明提出的算法具有良好的抗噪能力和高精度的检测能力。

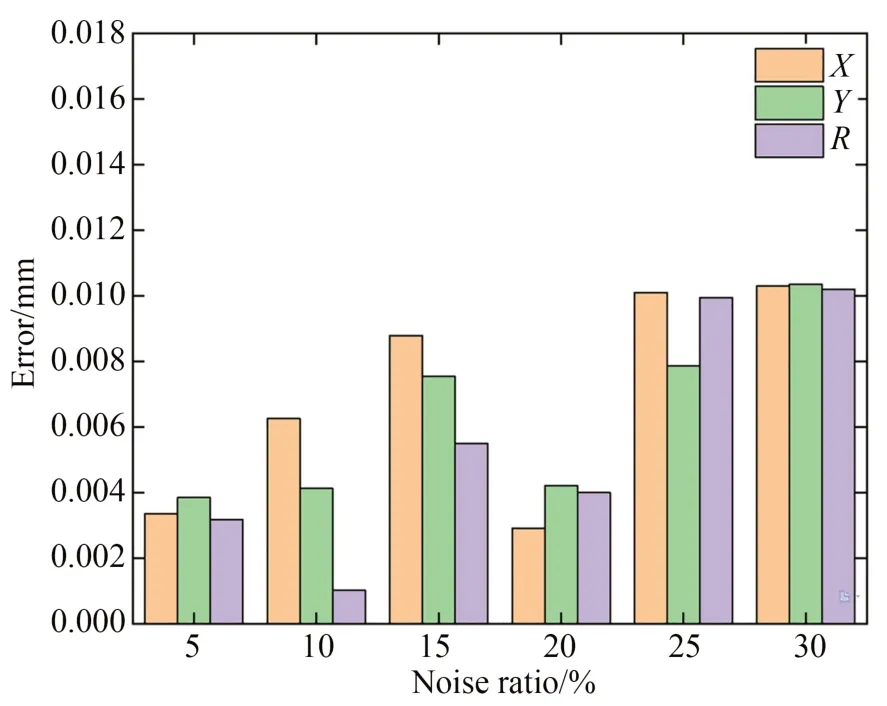
图11 不同椒盐密度对孔参数检测结果的影响Fig.11 Impact of different salt-and-pepper noise densities on detection results of hole parameters

受拍摄角度、光照条件等影响，拍摄得到的孔图像可能会包含部分孔内壁。由于内壁边缘与孔边界相似，常规算法可能会错误地将孔内壁的边缘识别为孔的一部分，导致误检或孔边界定位不准确。使用提出的算法对包含孔内壁的孔图像进行检测，结果如图12 所示。结果表明，本算法能够在不同的背景下准确区分孔内壁，具有一定的抗干扰能力。

图12 孔内壁干扰下的检测结果Fig.12 Detection results under interference of hole inner walls

稳定性实验结果表明，在孔图像具有不均匀光照，毛刺、污渍、划痕等孔缺陷以及噪声和孔内壁干扰时，本算法均能较好地检测出孔，稳定性较高。

3.2 质量和效率实验

为了评估提出算法的质量和效率，将它与Halcon 机器视觉库自带的Measure_circles 算法以及基于稳定RANSAC 算法的圆检测方法［22］进行对比，结果如图13 所示。为了方便区分，将这两种方法简称为H 方法和D 方法。

图13 不同方法的检测结果Fig.13 Detection results of different methods

在Measure_circles 算法中，首先使用快速阈值法对孔区域进行分割，然后使用Canny 算子提取感兴趣区域的亚像素轮廓，并判断轮廓的全局属性，筛选全局属性为类圆弧的轮廓，连接位于同一圆上的轮廓并计算轮廓点的坐标，最后使用最小二乘法进行圆拟合。

在基于稳定RANSAC 算法的圆检测方法中，引入一种基于形态操作的边缘掩模和一种通过划分扇区筛选轮廓点的方法，并使用RANSAC 算法进行圆拟合。RANSAC 算法是一种迭代的、稳定性较强的参数估计方法，用于从包含噪声和异常值的数据集中拟合数学模型，在圆检测算法中具有代表性。

实验对象是尺寸为660×640 像素的孔图像，分为4 组进行实验。由图13（a）可以看出，提出的算法能够准确检测多种环境和材料下的孔特征，具有较高的可靠性。对比3 种算法的检测结果，可以发现：在背景简单且光照效果良好的孔图像（第一组图像），3 种方法都能成功地进行检测。然而，当图像背景复杂，受到杂质或材料纹理等干扰，或者光照效果不佳导致孔特征与背景对比度较低时，H 方法和D 方法的检测精度明显下降。这种情况在第二组图像中较为明显，在第三组图像中甚至出现了锪孔外圆被误检为目标孔特征的情形。在最后一组人工制作的孔图像中，添加了毛刺、缺陷等孔缺陷以及15%的椒盐噪声，很明显D 方法无法完成孔检测。

表2 给出了3 种算法的孔半径检测误差。结果表明，本文算法在各组实验中的检测误差均小于其他两种方法，平均检测误差仅为0.011 mm，检测精度较高。表3 为3 种算法的检测时间。在第4 组图像检测实验中，由于D 方法无法成功检测，因此不进行比较。结果表明，虽然本算法的检测时间略长于其他两种方法，但4 组对比实验的平均时间成本仅为0.236 s，检测速度较快。

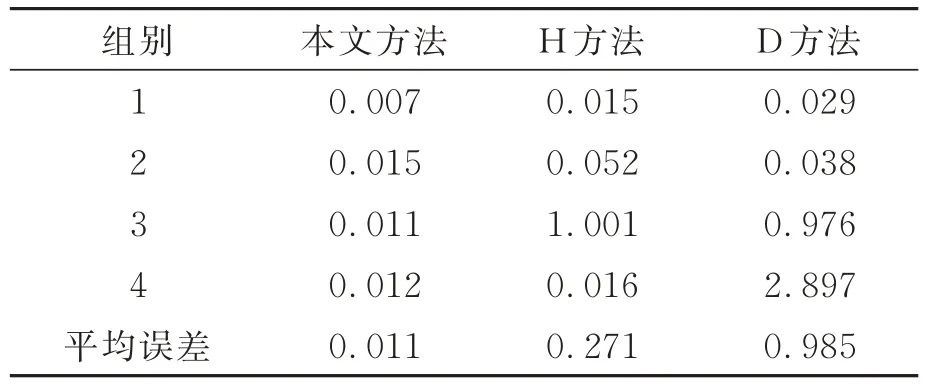
表2 各算法的孔半径检测误差对比Tab.2 Comparison of hole radius detection errors of various algorithms （mm）

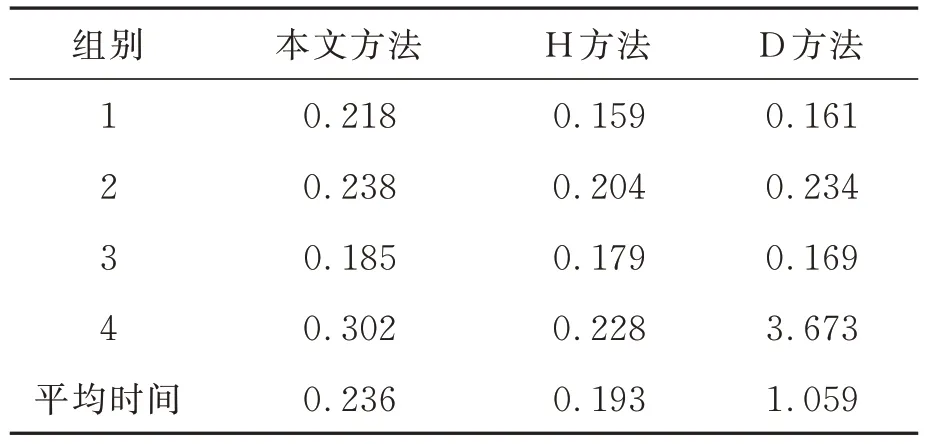
表3 各算法的检测时间对比Tab.3 Comparison of detection time of various algorithms （s）

质量和效率实验结果表明，与H 方法和D 方法相比，本算法能优先保证高质量的孔检测，同时检测用时也较短，0.236 s 的平均检测时间对于航空制造中的孔检测已经足够了。

4 结 论

本文提出了一种适用复杂航空制造场景中的航空零件孔特征检测算法。该算法将视觉显著性、数学形态学、Meanshift 和群决策有机集成和融合。通过在经典的FT 算法基础上增加图像增强步骤，并基于各像素与最大显著区域中心的距离确定各像素的权重，可以获得能够极大突出孔特征的全分辨率显著图，有效减少划痕、毛刺等对孔检测的干扰，有助于在后续阈值分割中提取完整孔区域。开发的具有多尺度多结构元素的新型数学形态学边缘检测算法结合轮廓细化算法，可以有效细化轮廓，去除一些非关键的孔特征轮廓点，在简化后续处理过程的同时，提高了算法的拟合精度。在圆拟合时采用Meanshift 算法寻找圆心，引入群决策模型计算圆孔半径，具有一定的抗干扰能力，即使基于在复杂背景下提取的复杂轮廓点，也能实现高精度圆拟合。该算法在面对不均匀光照、各类孔缺陷和孔内壁干扰的情况下具有较高的稳定性，在噪声密度高达30%的情况下仍能成功完成孔检测，且圆心坐标和半径的检测误差均在0.012 mm 以下。与现有的孔检测算法相比，该算法适用于在航空制造场景中多种孔图像的高精度检测，稳定性较高，检测速度较快，平均检测时间仅为0.236 s。

在实际工程应用中，需要注意本算法的参数选择和调优，如融合Meanshift 和群决策的轮廓拟合算法中的扫描半径和预设值。未来可进一步改进该算法中的显著值计算过程和Meanshift算法的迭代过程，有望进一步减少检测时间，提高孔特征的检测效率和精度。