星载InSAR 基线构型测量误差模型与灵敏度分析

鲍 捷， 刘兴潭， 陈建武， 李 林， 赵春晖

（北京控制工程研究所 空间光电测量与感知实验室，北京 100190）

1 引 言

双天线干涉合成孔径雷达（Synthetic Aperture Radar，SAR）卫星用于实现全天候、全天时、高精度全球数字高程测量。卫星采用柔性长基线构型的InSAR 系统，基线长度和指向变化会严重影响雷达的成像质量和干涉测量精度［1-4］。为达到米量级的测高精度，InSAR 的基线长度测量精度须达到亚毫米量级，指向测量精度达到角秒级，必须对安装在支撑臂远端的副天线的位置和姿态进行动态精密测量。在天线位姿测量过程中，存在各种可能导致系统位姿估计偏差的误差源。空间应用环境差异性的影响，还会引入地面应用场合没有的误差因素。因此，必须针对引起基线测量误差的各种因素加以研究，完善基线误差模型的建立与误差分配，并分析误差在系统中的传递与影响［5-6］。

美国“航天飞机雷达地形测绘任务”（Shuttle Radar Topography Mission， SRTM）是经典的单星双天线InSAR 系统，使用姿态和轨道确定子系统（Attitude and Orbit Determination Avionics， AODA）提供必要的基线测量、姿态和轨道确定，为克服单目视觉测量在视线方向精度的不足，选择基于激光与视觉组合测量的方案［7］，并研究了系统高程测量误差的影响，相关文献虽然提及基线长度和指向误差对总SRTM性能有显著影响，并从系统总体高程精度影响层面给出了误差分配表，同时据此调整部件性能约束和后续校正系统设计［8-10］，但没有给出基于此方案具体进行基线确定的误差分析方法。中国科学院电子所开展了InSAR 长基线测量技术的研究，通过解析推导分析了基线长度和角度的精度影响因素及来源，但缺少定量分析与误差分配［11］。

影响测量系统的误差来源复杂，且彼此间存在非线性耦合。目前的精度指标分解常侧重于经验与试验，缺少全流程仿真闭环验证，在初期寻找指标分配最优方案的过程中，往往耗费较多人力物力亦不能满足实际需求［12］。因此，有必要开展基线测量系统测量误差量化分配方法的研究，定量评估各误差的贡献度，为方案设计、安装优化以及系统精度指标分配等提供支撑。本文通过数学建模解析推导与数值计算定量仿真给出基线确定过程中的误差源，对各误差贡献度进行评估以及误差定量分配。

2 基线测量方案与模型

2.1 基线测量模型建立

本文采用激光干涉和视觉组合的测量方案，系统坐标系由它在卫星平台上的安装方式决定。双天线系统中两侧的基线测量系统相同，单侧系统组成如图1 所示，主要包括安装在卫星本体的测量系统和星敏感器，以及安装在天线平台端的靶标组，平台之间通过可伸缩天线臂连接。为对基线矢量进行建模，建立单侧基线测量系统坐标系如图2 所示。其中，基线测量系统涉及表1 所示的8 组坐标系。

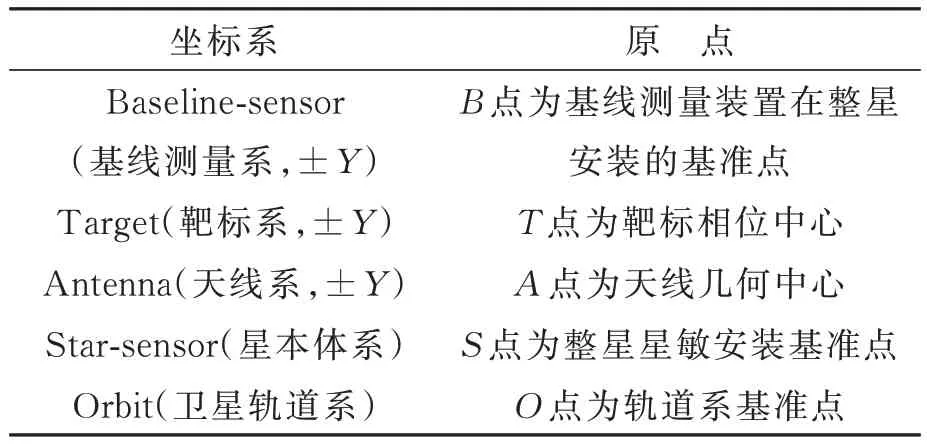
表1 系统坐标系定义Tab.1 Definition of coordinate system

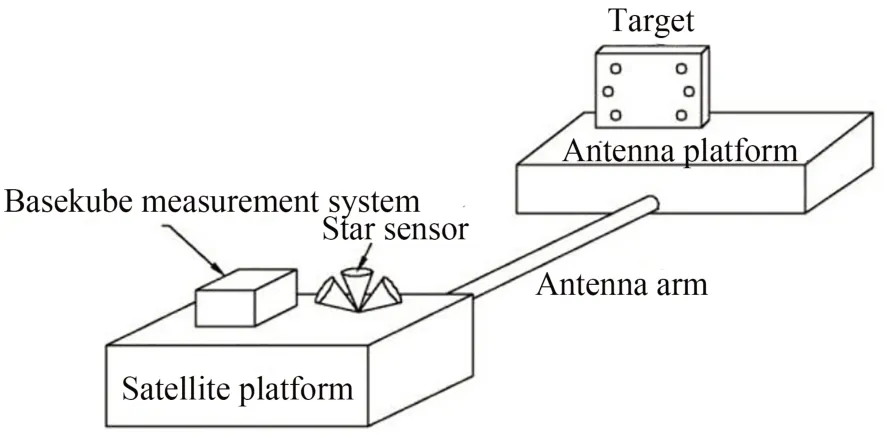
图1 双天线InSAR 基线测量系统（单侧）示意图Fig.1 Baseline measurement system of InSAR（one side）

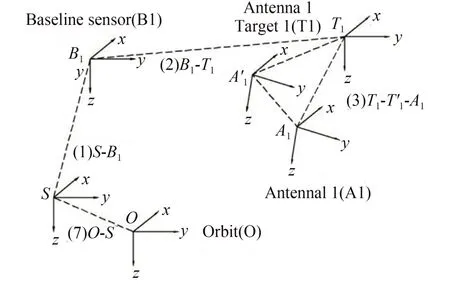
图2 基线测量系统坐标系（右侧）Fig.2 Baseline measurement system coordinates（right side）

天线中心与靶标中心安装并不重合，实际工作中需要考虑天线形变带来的测量误差。图2中，A'坐标系为原始安装条件下的天线几何中心，A为在轨运行中因天线变形导致天线中心发生变化后的实际天线本体坐标系。A'-T的转换关系通过地面标定已知，A-A'的转换关系可通过天线端安装星敏测量角度变化计算得到。因此，A-T之间的转换可以通过A-A'-T完成。

各个坐标系的转换关系与相应的矢量定义如表2 所示。

表2 坐标系转换关系定义Tab.2 Coordinate transformation definition

2.2 误差传递模型

测量误差在坐标系转换过程中传递，建立坐标系转换关系式推导误差在转换中的变化。通过其中一侧5 个坐标系之间的转换关系可以得到轨道系与天线系之间的关系：

其中：ROA=ROS RSB RBT RTA'，TOA=ROS RSB RBTRTA'TA'A+ROS RSB RBTTTA'+ROS RSBTBT+ROSTSB+TOS。

在双天线InSAR 系统中，空间基线为两侧天线相位中心的矢量连线，如图3 所示。根据式（1）可得：

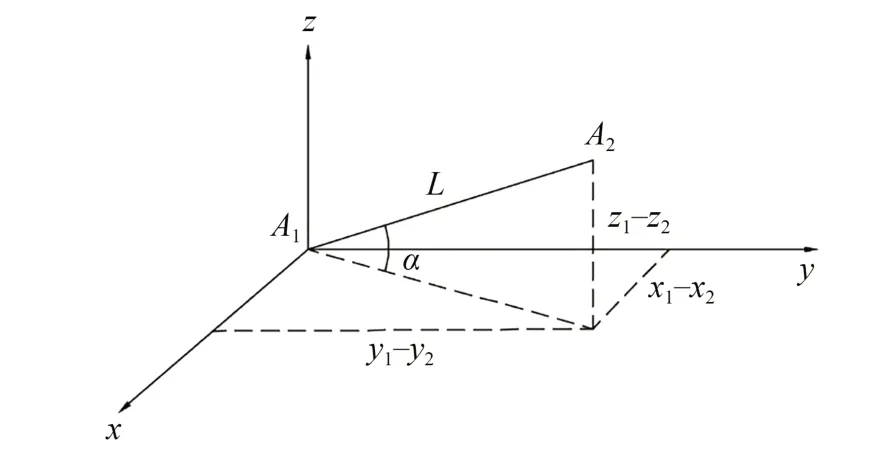
图3 双天线InSAR 基线示意图Fig.3 Baseline of dual antenna InSAR

则基线长度为：

基线角是基线矢量与水平面的夹角，利用式（3）中得到的基线各方向位置TA1A2_x，TA1A2_y，TA1A2_z，通过反正切三角函数关系计算得到基线角度：

3 解析推导与误差源分析

由式（2）和式（3）可得基线长度为：

对其中一侧求偏导，可得基线长度误差ΔL为：

将式（5）代入式（4）可得：

基线角误差ΔJ即为：

同理基线角度误差可以表示为：

其 中CJ为 系 数 矩 阵 ，CJ=

设向量μ，λ，δ分别表示旋转矩阵RSB，RBT，RTA中的角度误差矩阵，ΔTSB，ΔTBT，ΔTTA分别为平移向量TSB，TBT，TTA中的位置误差。单侧基线长度误差可以表示为：

对于三维矢量μ，λ，δ引入反对称阵概念。以μ为例，μ=（μx，μy，μz）3 个分量可以构成其反对称阵μx且两矢量之间满足a×b=axb=-bxa。

系统中主要的动态误差来源于测量系统与靶标系之间的动态跟踪误差，μ，δ和ΔTSB，包括测量装置的测量误差，在轨运行中机械振动以及热致震颤等微小扰动。ΔTTA主要来源于前期安装和标定，可视作静态误差。将基线误差按不同误差来源分类，可以得到：

其中：D=ROS RSB[1-(RBT(RTA'TA'A+TTA'))x]，由于天线抖动时角度变化较小，此时正弦项与余弦项可近似为：sinα≈α，cosα≈1，则旋转矩阵可以简化为I式加上一个小角度矩阵，如I+A，其他转阵类似。3 个转阵相乘则有RxRyRz=I+A+B+C+ABC，由于小量相乘趋近于零，将ABC乘积项省略，按小角度近似得到则有：

基线长度误差主要由天线相位中心Y方向 误差引起，而基线角误差主要由Z方向误差引起。据此可近似得到：

由此可知，影响基线测量精度的因素有：（1）系统标定残差，主要指系统地面安装位置标定手段和设备精度导致的各坐标系标定残差；（2）测量器件误差，测距精度直接影响Y方向结果从而影响基线长度结果，姿态角误差在Y方向上引入的分量也会间接影响长度精度；（3）天线相位中心误差，考虑远端天线在天线臂展开后发生的姿态改变，这部分误差主要受力热变形和长期稳定漂移影响；实际的天线相位中心不可测，其偏移还受电子器件稳定性的影响，导致天线波束扰动产生随机误差。

不同的误差源在误差传递过程中对测量结果的影响不相同，因此本文提出系统误差分量灵敏度的概念，定量分析误差源的贡献。

4 误差灵敏度分析

基线测量误差在坐标转换中传递。基线长度的表示中涉及7 组旋转矩阵与平移矩阵，每个矩阵涉及3 个自由度，共42 组自由度，包括长度与角度分量，共计84 个变量，变量数量繁多且每一项携带的误差对最终基线长度与角度测量结果带来的影响各有不同。并且误差模型中包含非线性项，难以直接利用微分法推导各项误差与精度的关系。因此，本文运用随机化法快速准确地量化分解精度指标，定量评估各误差贡献度，以保证高精度测量方案的可行性与稳定性。

误差灵敏度定义为其中一个变量产生的偏差对最终基线长度或角度测量结果产生的误差，反映每一个变量对测量精度的贡献。将灵敏度作为影响系数参与到后续误差分配计算中。通过上述对坐标系转换位姿，在综合位置灵敏度（3σ）与姿态灵敏度（3σ）范围内随机分配误差量（随机过程保证零均值正态分布，标准差为1σ）。表3 为根据实际测量值或经验值进行预分配，通过误差合成结果检验误差分配是否与预期结果相符，再通过多次迭代得到的误差分配结果。基线测量系统误差定量分析的仿真流程如图4所示。

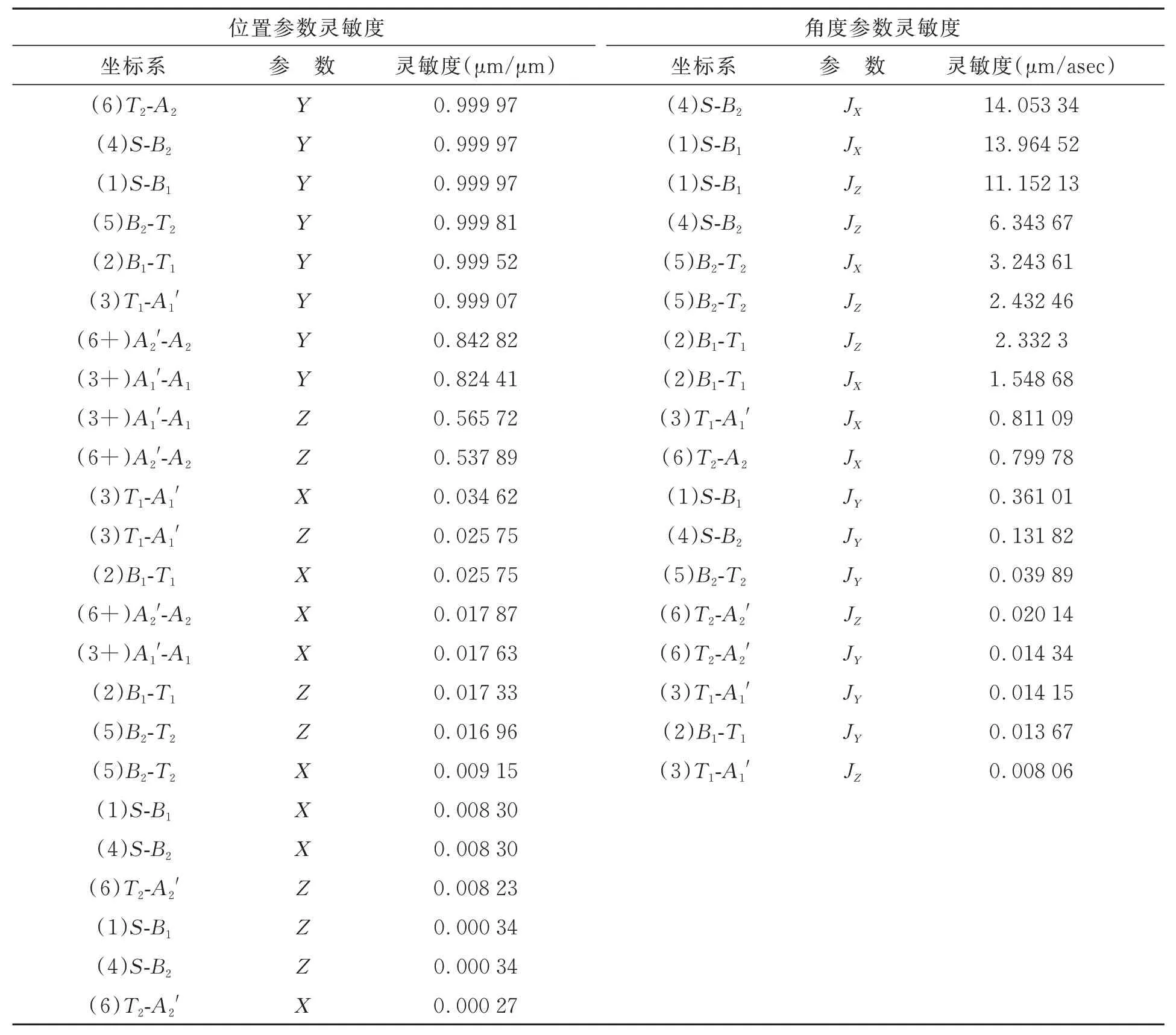
表3 基线长度误差灵敏度Tab.3 Baseline length error sensitivity

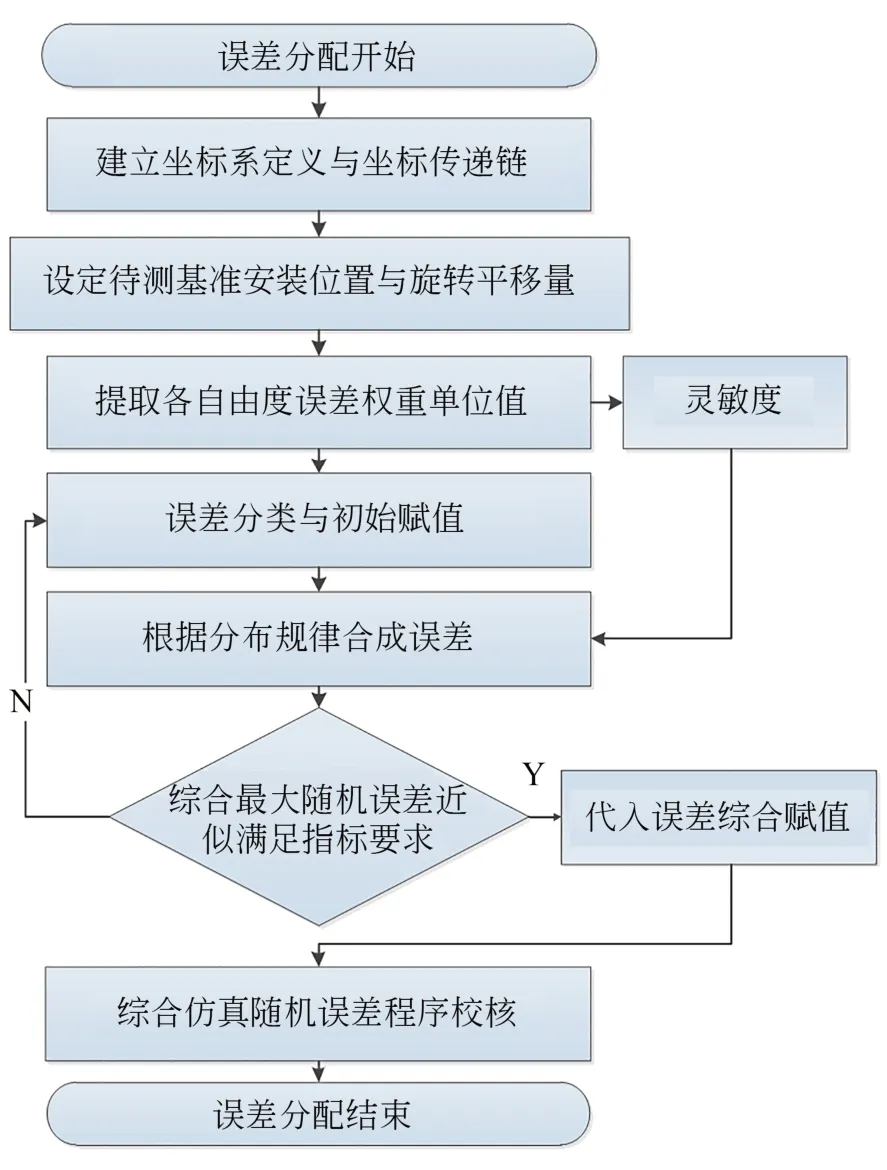
图4 误差分配与仿真流程Fig.4 Error distribution and simulation flow chart

对基线模型进行灵敏度计算，结果如表3 和表4 所示。表3 给出了基线测量系统测量天线臂在120 m 距离下，各坐标系六自由度参数对基线长度误差灵敏度的计算结果，由于单位不同又分为角度参数灵敏度和位置参数灵敏度，并按灵敏度数值降序排列。

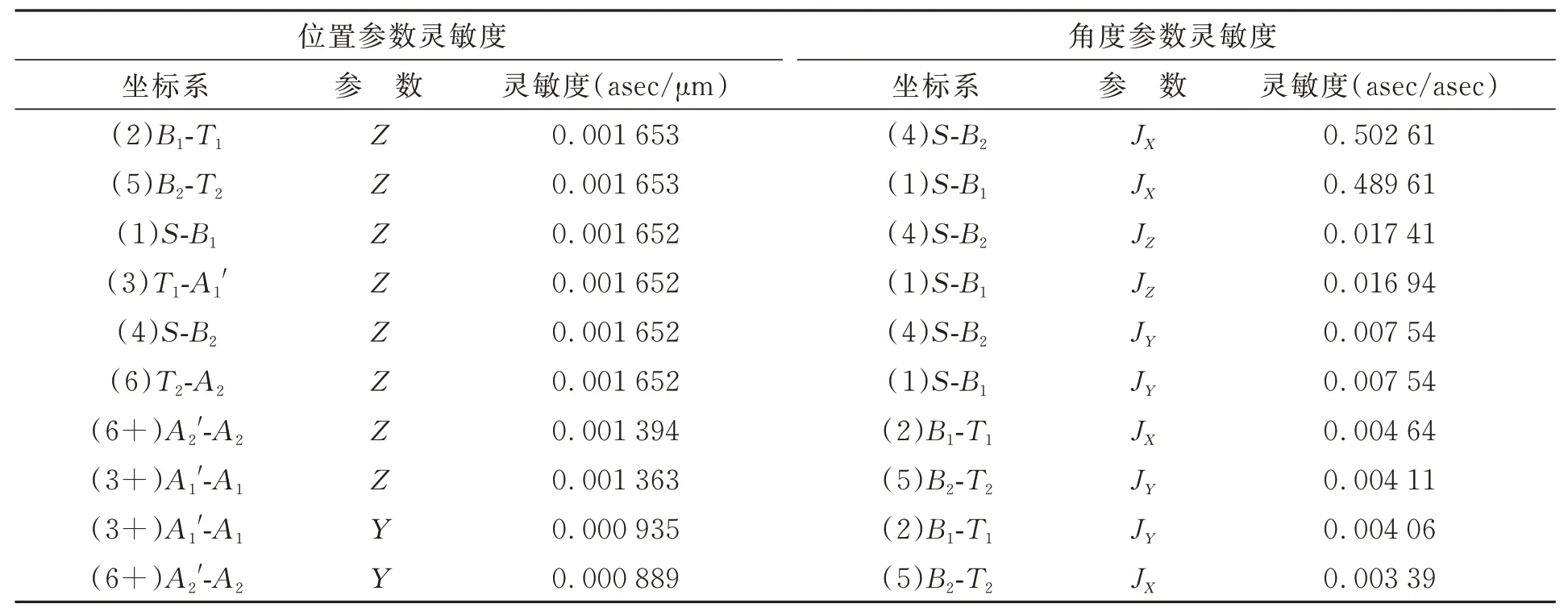
表4 基线角度误差灵敏度Tab.4 Baseline angle error sensitivity

从表3 中可以看出，较大的位置灵敏度主要集中在Y方向，即距离方向，该方向上位置误差对基线长度的影响将近1∶1，单轴位置偏离1 μm，基线长度将产生近1 μm 的误差。角度对基线长度的影响方面，有关测量系即B系的俯仰与偏航角灵敏度较大，最大能达十几微米每角秒，即单轴每产生1″的角度测量误差，会给基线长度结果带来十几微米的误差。

表4 展示了各坐标系六自由度参数对基线角度误差的影响灵敏度计算结果。结果显示，位置参数在Z轴方向的影响较大，比其他位置高至少一个量级。而角度参数影响方面，测量装置在星本体上安装标定等带来的俯仰角度误差贡献最为突出。比起解析式，灵敏度表格为系统精度分析提供了更直观的参数影响，系统的结构设计调整以及误差分配等工作均可以在此基础上进行。

表3 和表4 中灵敏度计算中给定的基线测量系统到星本体系三轴角度真值均为1°，为探究这些角度对灵敏度是否有影响，计算了基线测量系统相对星本体系三轴角度分别在-90°到90°条件下基线角度灵敏度、基线长度灵敏度的数值，并将最大、最小值标注在图上，结果如图5～图6所示。

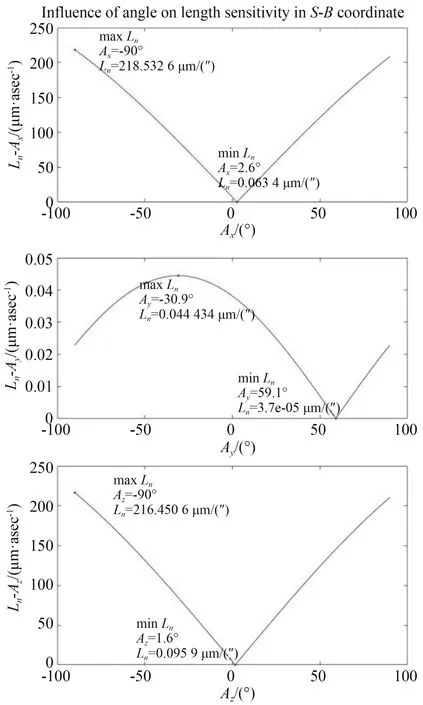
图5 测量装置相对星本体系安装角度对长度灵敏度的影响Fig.5 Influence of installation angle of measuring device on length sensitivity

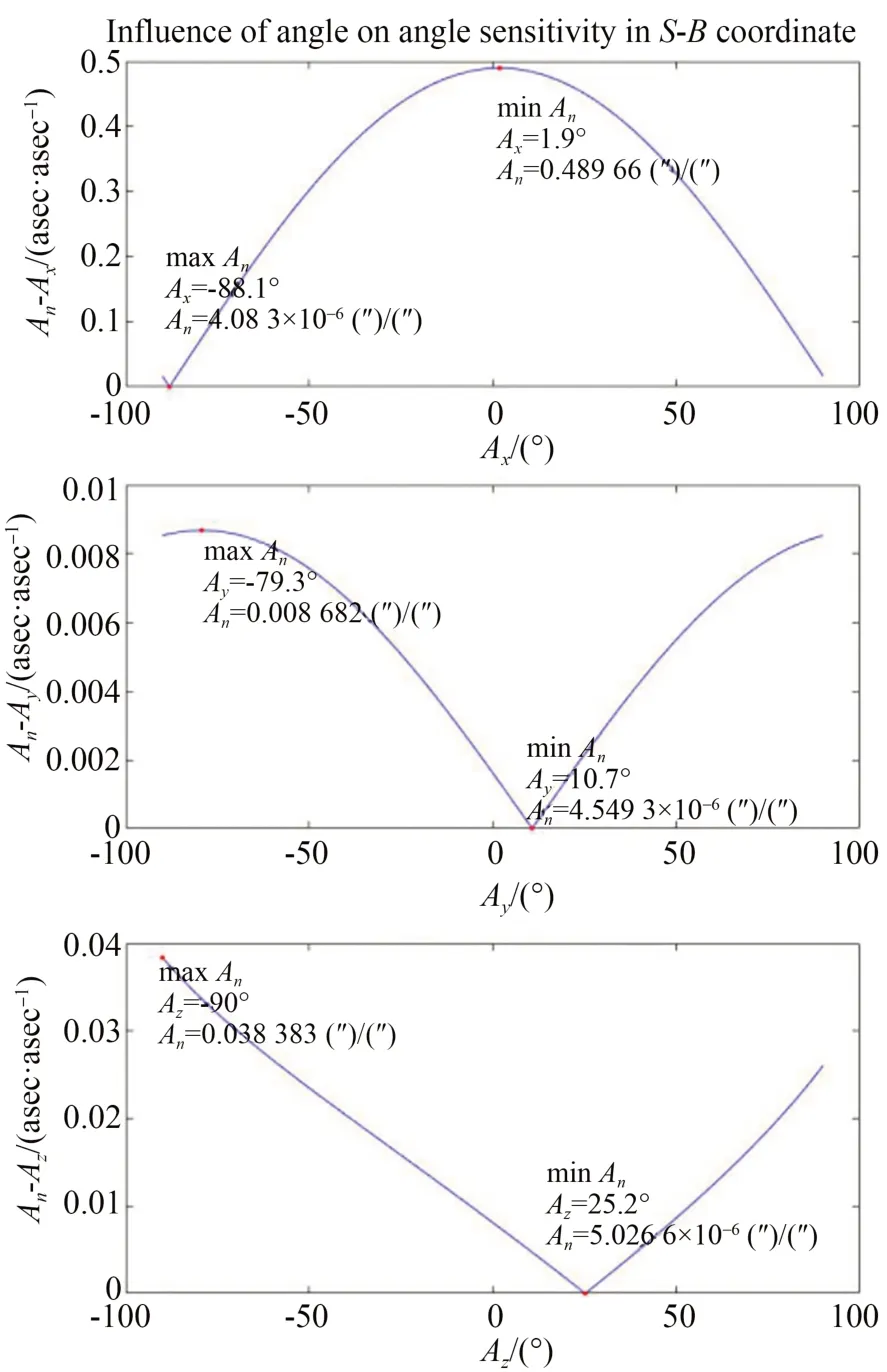
图6 测量装置相对星本体系安装角度对角度灵敏度的影响Fig.6 Influence of installation angle of measuring device on angle sensitivity

从图5 中可以看出，安装角度确实对长度灵敏度有影响。Y轴灵敏度最大为0.044 μm/（″），低于X轴Z轴灵敏度最小值，其他角度处更是差出数个量级。X，Z轴最小值在2.6°与1.6°处，且角度越靠近两端灵敏度越大，对基线长度误差的影响就越大，因此考虑基线长度误差较小的情况下，1°的安装角度是较为合适的。

从图6 中可以看出，安装角度对角度灵敏度也存在影响。X轴灵敏度峰值在1.9°位置，Y，Z轴则是灵敏度谷值更靠近零点，分别为10.7°和25.2°，且三轴角度影响趋势与量级不一致，很明显X 轴角度灵敏度比其他两轴高一到两个量级，这也能说明为什么在三轴均为1°时X轴角度灵敏度比另外两轴大一个数量级。从图中也能看出，三轴角度均设计为1°并不是灵敏度最优选择。真值的设计可能会影响基线测量误差结果，为反演出最佳安装角度，将不同灵敏度数据代入基线角度误差求解过程中，根据计算得到的误差选择更优的三轴角度。很显然，灵敏度在各自的谷值处基线角度误差最小。越靠近±90°，X轴角度越小，但实际安装的俯仰角不可能这么大，应当在满足安装约束的前提下选择灵敏度尽量小的角度位置。同理也可以对其他参数进行分析，这一反演思路可为系统结构的设计与优化提供理论支持。

5 仿真分析

根据误差传递与灵敏度分析结果，综合考虑各误差源（假设相互独立且服从正态分布），得出一组误差综合影响案例：对标定残差、测量误差、力热变形和长期稳定漂移4 种影响明显的误差进行初步分配。系统误差主要考虑地面标定残差，随机误差关注器件性能、结构设计等引起的测量误差、力热变形、长期稳定漂移。根据系统的测量精度要求，这里给定的长度测量精度为1 mm，角度测量精度为2″（1.6σ），误差分配如表5 所示。由于篇幅有限，在此只列出部分分配结果。

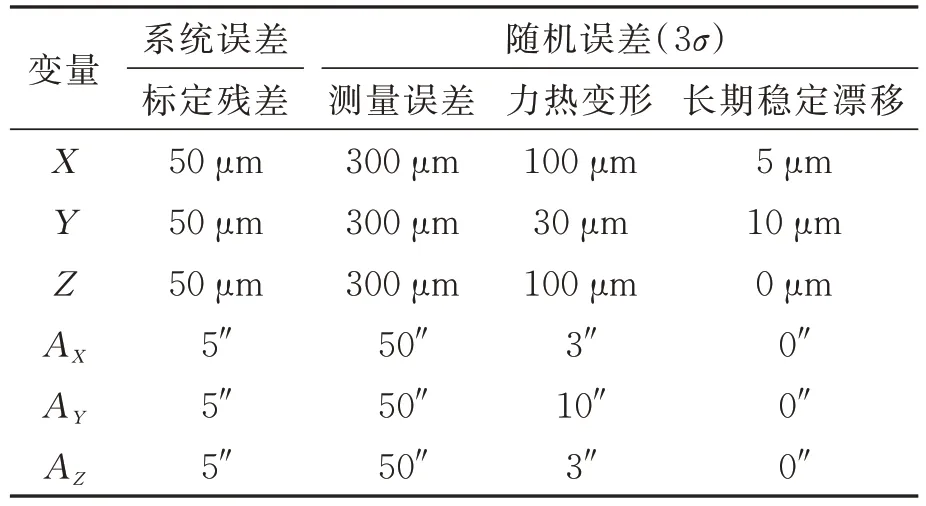
表5 误差分配（B1-T1）Tab.5 Error distribution（B1-T1）

为更贴近真实工况，验证理论推导计算与分配结果的合理性，通过蒙特卡洛法进行数值模拟仿真。蒙特卡洛法（Monte-Carlo）也称统计实验法，其基本思想是利用计算机的数值模拟来代替解析推导，在保证随机变量满足一定概率分布的情况下，通过大量仿真来研究随机参数在统计意义下的特性［13-15］。

代入表5 中分配的随机误差项之和作为对应坐标系间的误差输入，根据蒙特卡洛法，按照正态分布随机生成全局扰动，进行误差合成定量仿真，迭代2 000 次。在计算机仿真中，利用Matlab提供的random（）函数，产生服从标准正态分布的随机数序列以代表随机误差。当置信系数取1.6时，系统测量精度的仿真统计结果如图7 所示。

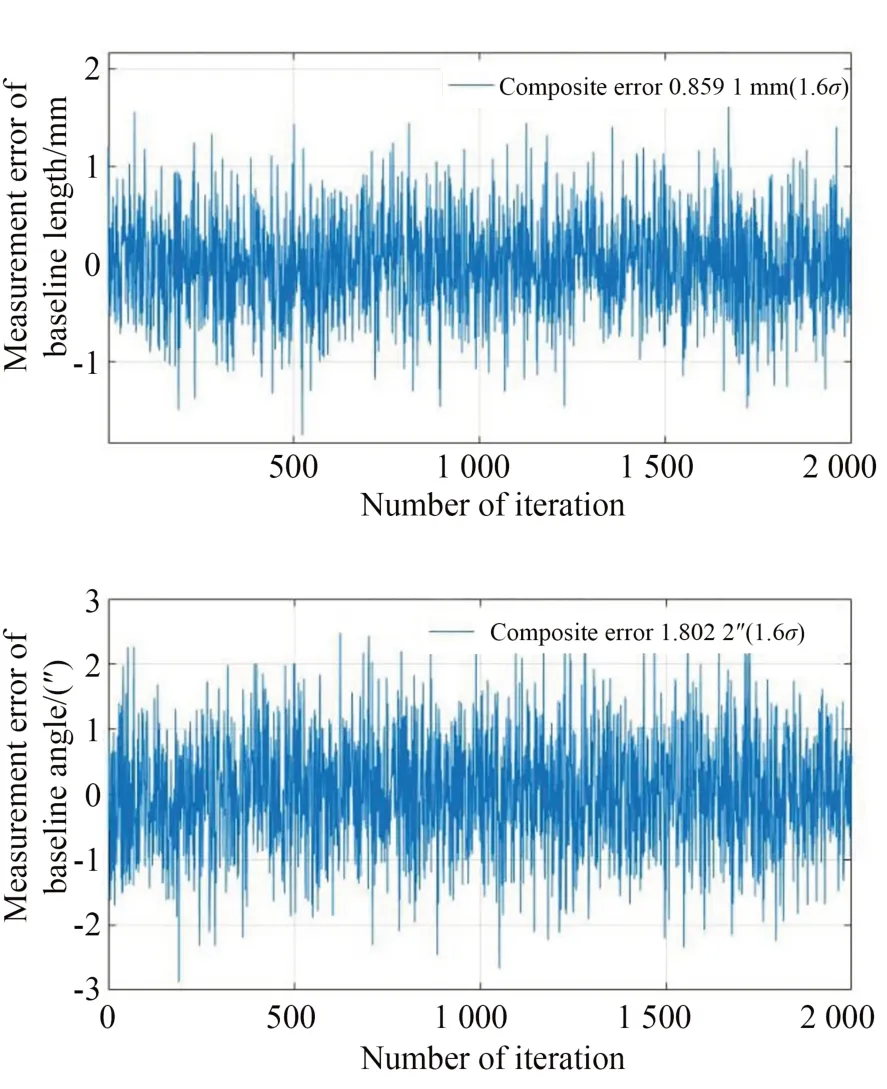
图7 基线测量综合误差合成仿真结果Fig.7 Synthesis simulation result of baseline measurement error

基于以上误差分配与灵敏度计算，得到基线测量系统长度的综合误差合成（std）仿真结果为0.859 1 mm（1.6σ），基线测量系统的角度综合误差为1.802 2″（1.6σ），满足给定的精度要求。同理，可分析反演出其他条件下所需的测量精度与误差分配方案。

6 结 论

星载双天线InSAR 系统基线测量中主要依靠实验统计与经验数据，缺少直接的函数解析式推导和直观的误差定量分析方法。本文通过基线测量系统模型与误差传递模型的建立，分析了空间基线误差来源，并给出了该模型的误差灵敏度分析。通过误差定量灵敏度计算明确了正向误差的传播途径，得到各误差项对总体精度的影响量级。对给定的总体精度指标要求，利用定量的灵敏度数值进行逆向误差分配反演，对各环节误差预算有整体把握，也可以据此对方案设计、安装标定参数和误差分配方案等进行优化。仿真分析结果表明，激光视觉三轴的位置测量精度为300 μm（3σ），角度测量精度为50''（3σ），即可满足基线长度精度为1 mm（1.6σ），基线角度精度为2''（1.6σ）的要求。然而，根据灵敏度逆向计算得到的误差分配结果不唯一，是否合理还需要通过实验在轨数据的支撑、反复迭代才能验证，但在方案论证阶段可以提供参数设计的数据支撑。这一误差分析方法与思路也可为其他类似空间相对位姿测量系统的指标制定与方案设计提供指导。