二自由度大行程无耦合压电粘滑定位平台

吴 彤， 杨依领*， 吴高华， 崔玉国， 魏燕定

（1.宁波大学 机械工程与力学学院 浙江省零件轧制成形技术研究重点实验室，浙江 宁波 315211；2.浙江大学 机械工程学院 浙江省先进制造技术重点实验室，浙江 杭州 310027）

1 引 言

作为微操作与微装配的关键技术之一，精密定位技术现已广泛应用于超精密加工［1］、生物显微操作［2］、光 学制造［3］、微机电系统［4］和生物医疗［5］等多个领域。目前，为满足宏-微-纳尺度的操控需求，运动行程大、尺寸紧凑、自由度多的高精度定位技术已成为研究热点。

在众多微纳操作应用中，压电驱动器因具有高响应、位移分辨率高、无磁性和结构灵活等优点而被作为常用的核心驱动部件［6-7］。但其尺寸和行程的兼容问题无法避免，在一定尺寸的限制下，运动范围较为有限。因此，为克服压电直接驱动时的输出行程有限问题，尺蠖驱动、超声驱动和粘滑驱动等受到了广泛关注［8］。

尺蠖驱动具有驱动方式稳定、驱动力大以及运动行程大等特点，但由于其需要多个压电元件互相配合才能实现驱动，存在结构尺寸大以及操作及控制复杂等弊端［9］。超声驱动常用于高速运动，但是其驱动频率较高，易于磨损［10］。与上述压电驱动方法相比，压电粘滑驱动结构紧凑、驱动单元少、使用寿命较长、工作行程大以及运动精度高等，具有较好的综合输出性能［11］。

Tian 等［12］设计了一种混联式二自由度压电粘滑运动平台，驱动单元采用并联解耦机构，并与滑块串联以实现运动解耦，同时采用压电预紧机构调整摩擦力大小。但其单步位移小，固有频率较低。Li 等［13］提出了一种压电粘滑式惯性运动平台，利用摩擦力与惯性力之间的差异运动来进行快速定位。但该类粘滑驱动平台只能实现单自由度运动，且单步位移较小。Lu 等［14］将非对称柔性铰链与桥式位移放大机构相结合，设计了一款直线压电粘滑台。桥式机构增加驱动过程中的预紧力，并且可以放大输出位移。但所用的桥式机构放大倍数较小进而导致单步位移小，且仅可实现单个自由度运动，平台承载能力低，分辨率也较低。

随着微纳操作技术的快速发展，多自由度运动已成为高精度定位平台的重要特性。常见的二自由度驱动机构的结构主要分为串联式和并联式［15］。串联式可以单独控制每个方向的运动，但其各向输出异性，且首级自由度惯量较大，削弱了平台的动态输出性能［16］。并联式各向输出特性一致，且共用一个驱动机构来实现多维运动，具有精度高、惯性小、体积小以及承载能力高等优点，已广泛应用于高精度定位平台上［17-18］。但是，并联式存在运动耦合，需设计相应的解耦机构减少寄生位移［19］。

针对目前粘滑驱动单步位移较小、运动自由度少以及存在并联耦合等问题，本文设计了一种二自由度大行程无耦合压电粘滑定位平台。通过桥式柔顺放大机构设计驱动单元以增加单步输出位移，并采用并联解耦方式减小各向运动的交叉耦合误差。同时，利用粘滑驱动原理设计定位平台结构，并通过预紧机构调节接触表面之间的摩擦力，进而提高定位平台的粘滑运动性能。

2 结构设计及其工作原理

2.1 结构设计

作为粘滑定位平台的关键部件，驱动机构主要由桥式放大机构和并联解耦机构构成。传统的单层直圆式桥式放大机构（SCBTA）如图1（a）所示。然而，其横向刚度较低，受外部载荷时可能会损坏压电驱动器。类似地，单叶型桥式机构（SLBTA）的固有频率也较低，影响结构稳定性，见图1（b）。本文设计了结构紧凑、且横向刚度大的拱形桥式放大机构（ASBTA），如图1（c）所示。该机构具有双层桥式结构，以提高其横向刚度。每个桥式支臂均由一个刚性连杆和两个半圆形柔性铰链组成，结构紧凑，且能够提高结构频率。此外，对称布置的方式利于良好的导向性能，并且可通过调节桥臂与水平线的夹角，获得不同的放大倍数以及输出位移方向［17］。

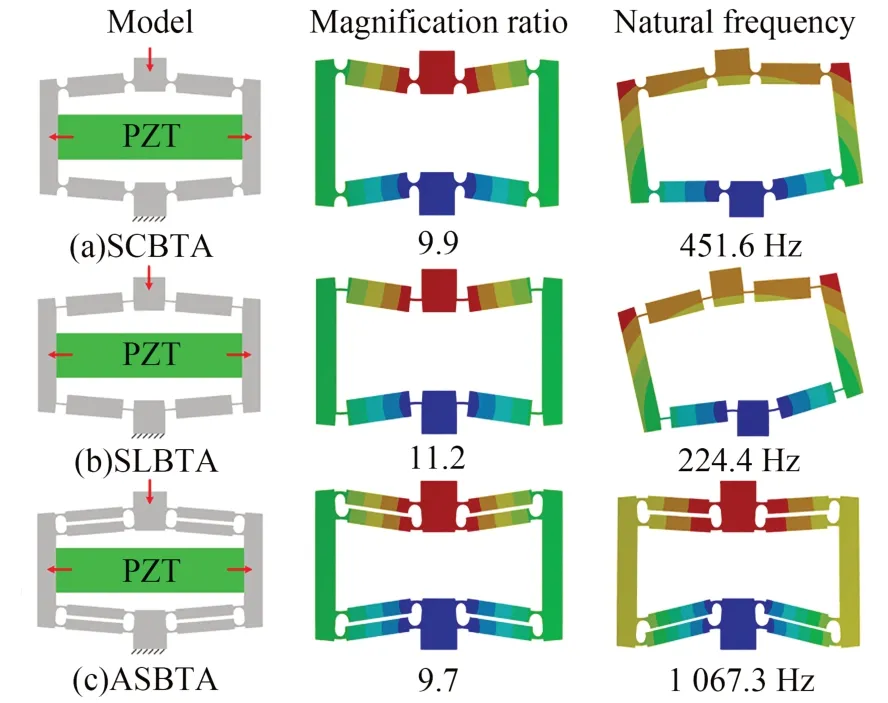
图1 不同放大机构的对比Fig.1 Comparison of different amplifiers

采用上述拱形桥式机构，图2 给出了设计的二维柔顺驱动机构。它由半圆形柔性铰链构成的桥式放大机构、叶型柔性铰链组成的复合解耦机构、压电驱动器、楔块、输出平台和连接块等组成。驱动机构采用4-PP 并联结构（P 代表移动关节），并将对称平行叶型铰链（SPLH）作为P 关节。x和y向均设有桥式放大机构，以保证输出平台在每个自由度上均具有较大的输出位移。压电驱动器在W1，W2处产生输入位移，经桥式机构放大后传递到W3处，从而推动中央平台沿y向移动。采用复合平行四边形机构进一步提高解耦性能，以消除x向运动的输出耦合以及沿整个运动链的不必要寄生运动。此外，解耦机构双层布置，有利于增加结构刚度，以保证柔性驱动机构运动时的稳定性。

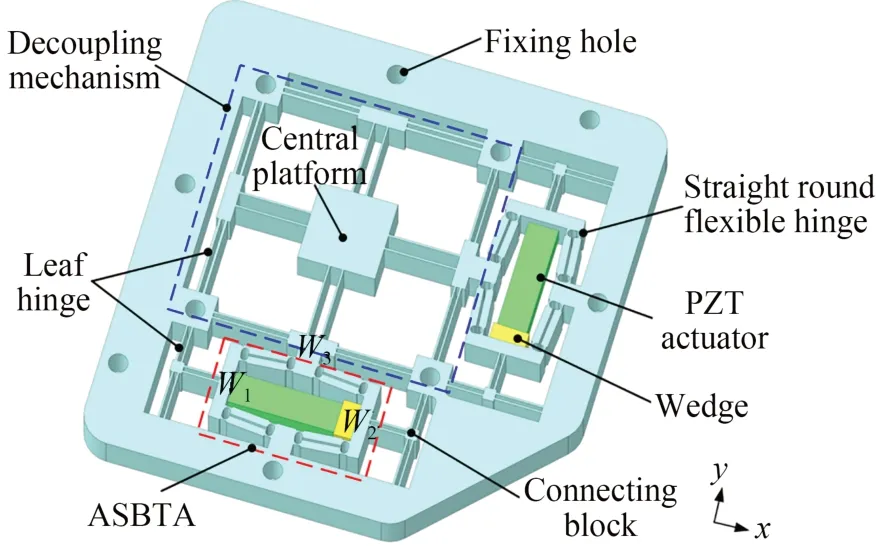
图2 二维柔顺驱动机构Fig.2 Two-dimensional compliant driving mechanism

由于x，y方向结构相同，两个自由度上的驱动性能类似。压电驱动器工作时，沿驱动方向的内部SPLH 由于纵向刚度高，可以将运动传递到输出平台。而垂直于驱动方向的SPLH 由于横向刚度低，将作为移动关节，从而降低交叉耦合误差。最终，可获得大输出位移、低耦合比以及高频响的二维柔顺驱动机构。

图3 为二自由度大行程无耦合压电粘滑定位平台，该平台主要包括柔顺驱动机构、移动台、交叉滚柱导轨、底座以及一系列连接件。交叉滚柱导轨和连接件用于连接移动台与驱动机构，并形成导向轴平动式方法对移动台进行导向及运动解耦，使平台结构紧凑，x与y向运动之间无耦合，运动惯量大大减小。由于粘滑平台的输出性能很大程度上取决于驱动机构上施加的摩擦力，因此，设计底部带有柔性铰链的移动台，并与预紧螺钉配合调整接触面上的摩擦力。当预紧螺钉上下调整时，移动台与驱动机构中央平台之间的压力减少或增加，从而调节两者接触面上的摩擦力。

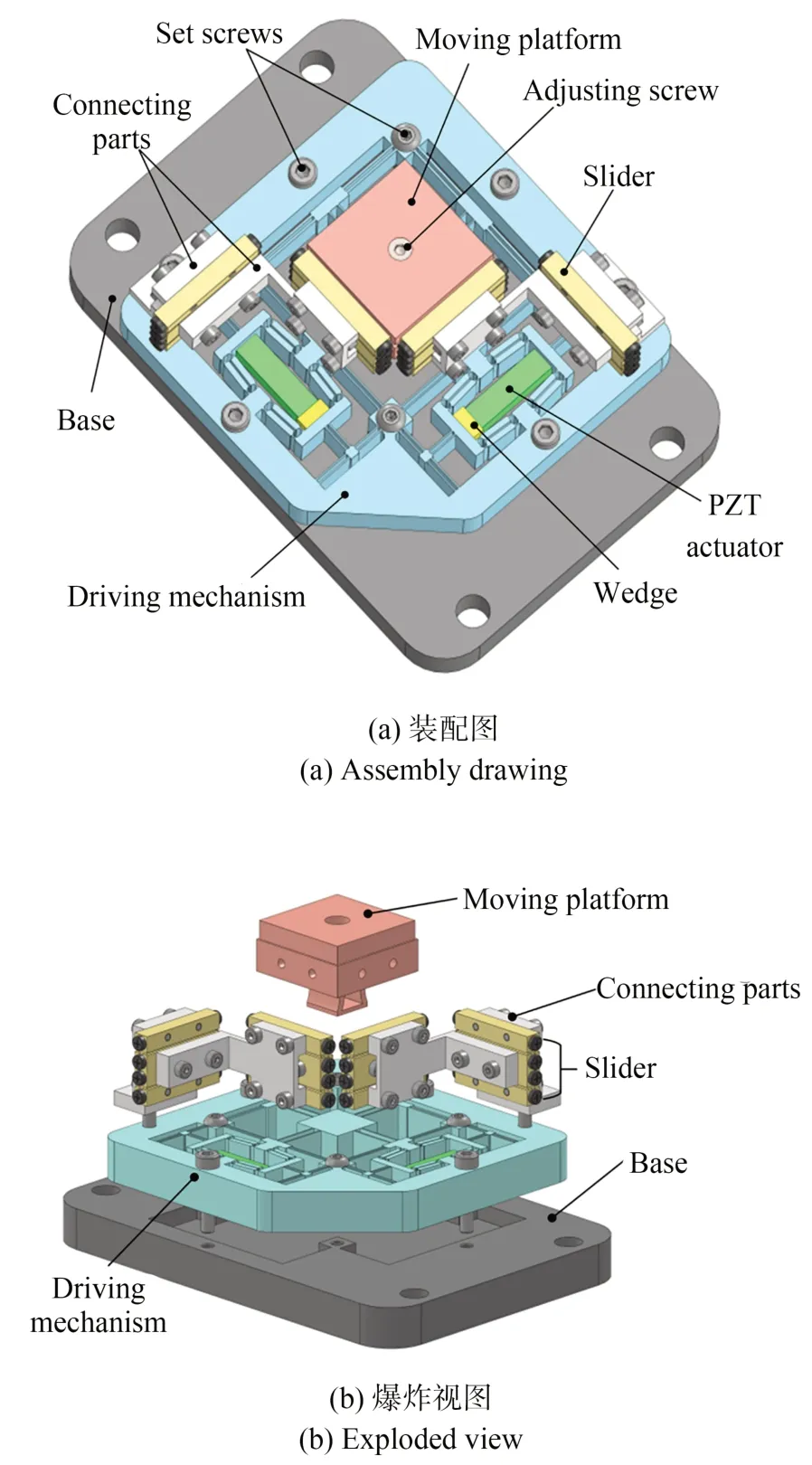
图3 粘滑定位平台Fig.3 Stick-slip positioning stage

对桥式支臂倾斜角度、直圆柔性铰链半径、连杆长度、叶型柔性铰链长度以及厚度等重要结构参数进行多次有限元仿真，最终得到驱动机构的关键尺寸，如表1 所示。其中，lBD，lEF，lKL，lMN，lOP和lQR为叶型铰链BD，EF，KL，MN，OP和QR的长度，t1～t5为叶型铰链厚度，t6为直圆铰链厚度，lAB，lBC和lGH为刚性连杆长度，r为直圆柔性铰链的半径，α为倾斜角度，如图4 所示。

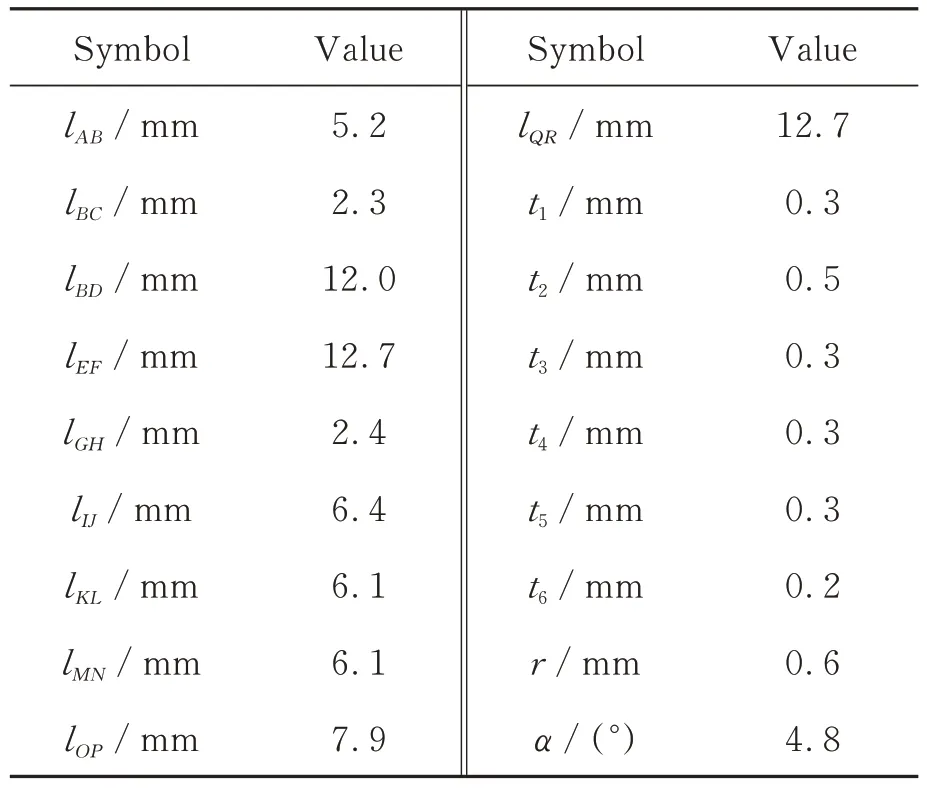
表1 驱动机构的关键结构尺寸Tab.1 Key structural parameters of driving mechanism

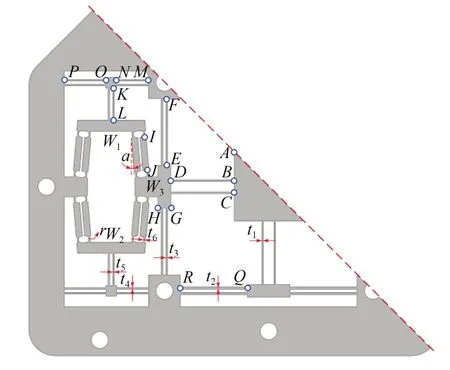
图4 驱动机构的关键尺寸Fig.4 Key parameters of driving mechanism

2.2 工作原理

定位平台利用粘滑驱动原理进行运动，其工作过程如图5 所示。

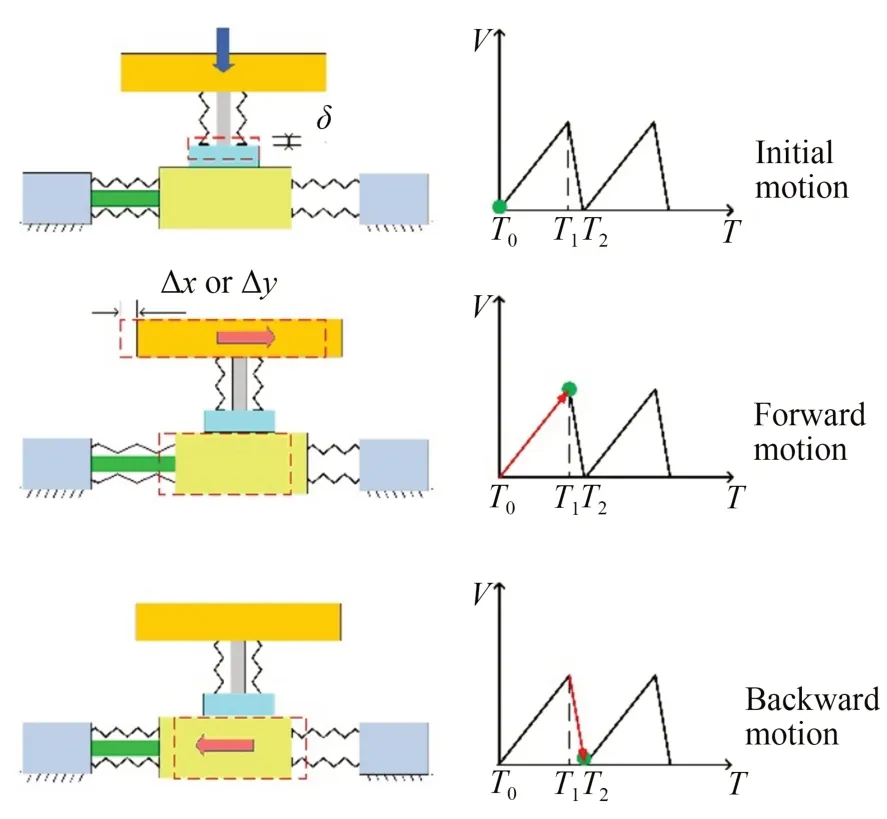
图5 粘滑运动原理Fig.5 Stick-slip motion principle

（1） 初始阶段：在T0时刻，驱动电压幅值为0，压电驱动器处于自然长度，调节预紧螺钉使移动台与输出平台接触。

（2） 粘贴阶段：由T0至T1，驱动电压缓慢增加，压电驱动器伸长，输出平台沿x或者y方向移动，由于静摩擦力的作用，移动台会向前移动。

（3） 滑动阶段：由T1至T2，驱动电压快速减小至零。压电驱动器和输出平台迅速回到起点。由于惯性作用，移动台停留并产生一个净位移。

不断重复粘滑运动过程（1）～（3），定位平台会产生连续输出位移，最终实现大范围运动。

3 理论建模

采用有限元理论对驱动机构进行静力学建模，柔性铰链和刚性连杆视为包含两个节点的柔性单元［2］。依次连接各柔性单元，得到图6 所示的有限元模型。

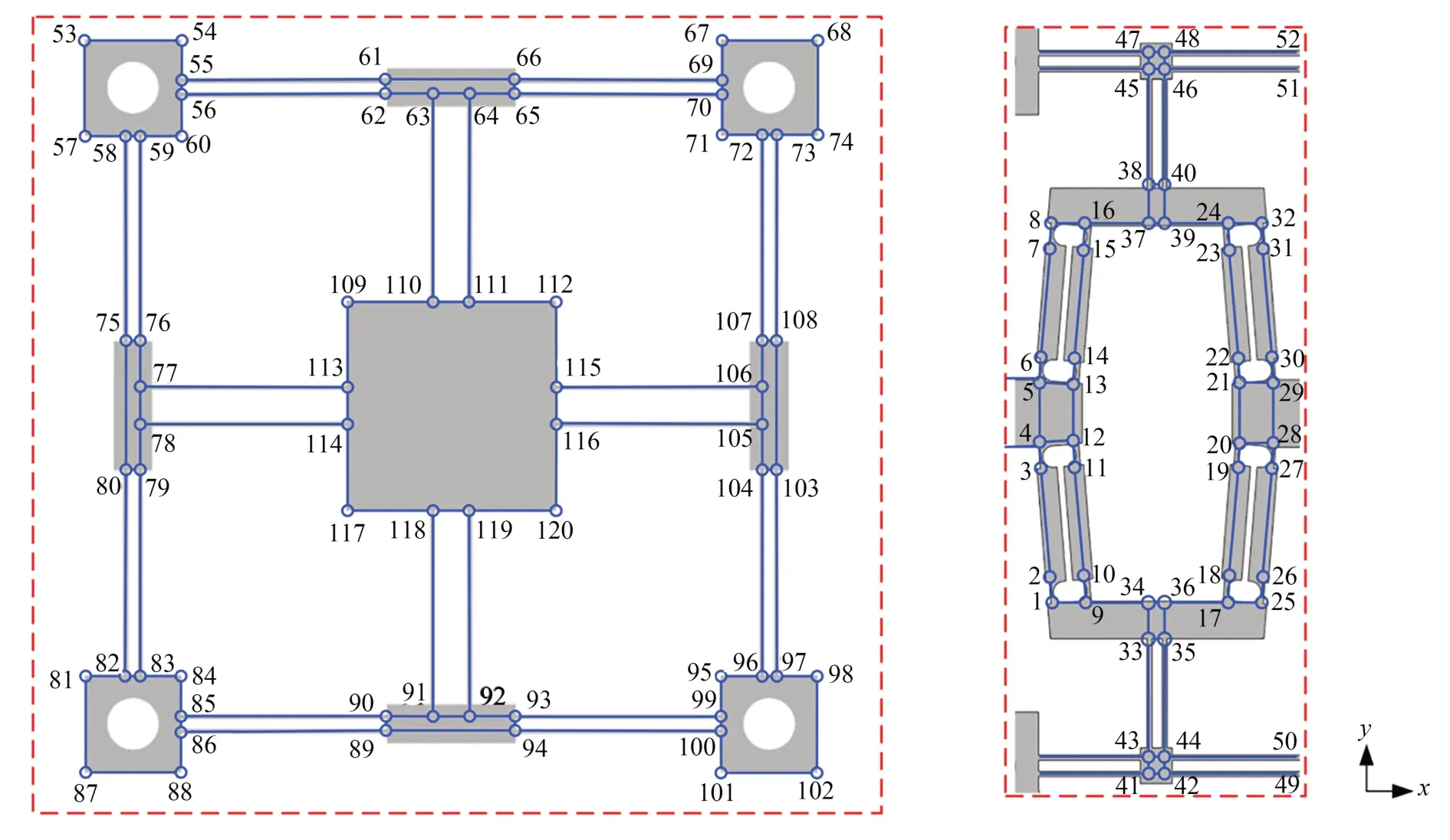
图6 驱动机构的有限元模型Fig.6 Finite element model of driving mechanism

叶型铰链和刚性连杆简化为梁单元，弹性模量、截面面积、惯量矩和连杆长度分别用E，A，I和l表示，则刚度KL表示为：

与此同时，半圆形柔性铰链简化为铰链单 元，刚度KC为：

式中：C1～C4表示相应力所产生的位移参数，R1=C1C3-C22，R2=2RC2-C3。

若要得到全局坐标系下的刚度矩阵Ke，需对局部单元刚度矩阵KeT转化，即：

式中：T是转换矩阵，具体表达式为：

式中α表示从全局坐标系到局部坐标系时顺时针转过的角度。

总刚度矩阵K的建立步骤如下：

（1） 将驱动机构依次进行分解、标记节点如图6 所示；

（2） 建立每一个单元的单元刚度矩阵，并将其转换到全局坐标系下；

（3） 将全局单元刚度矩阵分成4 个子块：

（4） 将局部单元刚度矩阵按照顺序对应放置；

（5） 处理边界条件并求解。对于驱动机构，系统刚度矩阵需删除固定节点49～52，53～60，67～74，81～88 和95～102 所在的行与列。

外力F、总刚度K和位移Q之间的关系为：

式中：Fi和Qi为第i个节点的受力和位移，n为节点数量。

对节点34，36，37 和39 施加外力Ft，则驱动机构y向的输入位移Qin为：

式中Q34，Q36，Q37和Q39为节点34，36，37 和39 的y向位移。

驱动机构的位移放大倍数λ和输入刚度kin为：

式中Q112，Q115，Q116和Q120为节点112，115，116 和120 的x向 位 移。

当压电驱动器内置于柔顺驱动机构后，其实际输出位移ΔL为：

式中kp和ΔL0分别为压电驱动器的刚度以及标称位移。因此，压电驱动时输出平台的位移为λΔL。

4 仿真分析

采用Ansys Workbench 验证粘滑定位平台性能，移动台、驱动机构和连接件的材料为铝合金7075，密度为2 810 kg/m3、弹性模量为71.7 GPa 以及泊松比为0.33。导轨的材料属性为密度7 900 kg/m3、弹性模量210 GPa 以及泊松比0.3。采用交叉滚柱导轨，忽略了滑块与导轨之间的摩擦。同时，将驱动机构中央平台与移动台底面的接触定义为“摩擦”，结合摩擦副材料特性并参考文献［20-21］，摩擦系数设置为0.3。

对驱动机构两侧输入端各施加10 μm 的位移，平台x向输出位移为114.63 μm，位移放大比为5.7 倍；y向输出位移为110.07 μm，位移放大比为5.5 倍，如图7 所示。考虑到式（9）计算的理论放大倍数为5.2，理论计算与仿真分析的相对误差分别为8.8%和5.5%，如表2 所示。此外，x和y方向的最大耦合位移分别为0.10 μm 和0.07 μm，耦合比分别为0.09%和0.06%，平台具有良好的平动解耦特性。

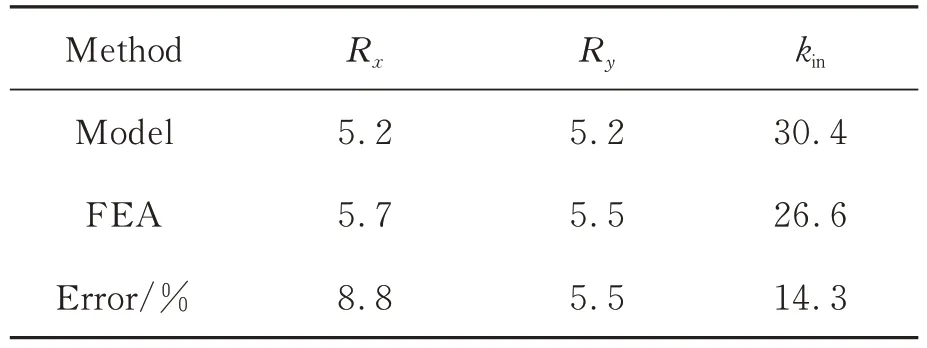
表2 位移放大倍数和刚度Tab.2 Displacement amplification ratio and natural frequency

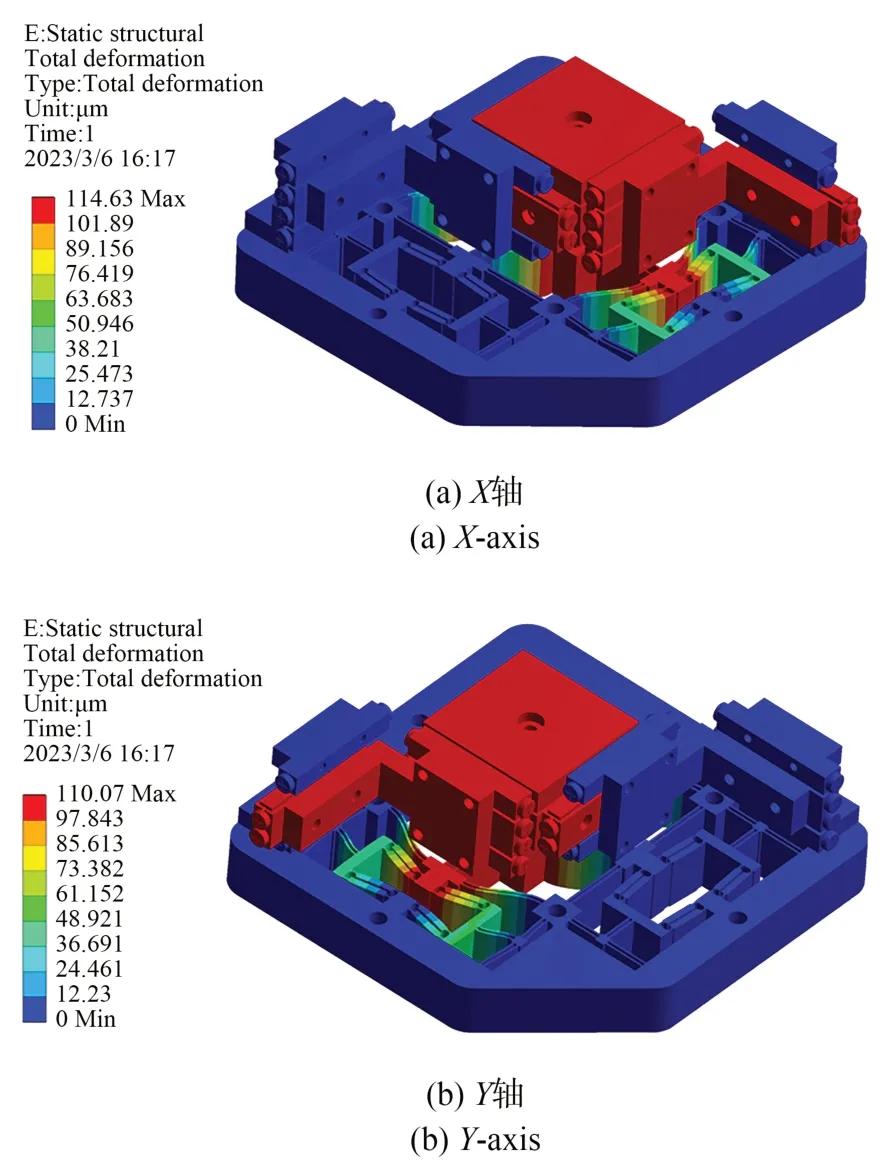
图7 输出位移Fig.7 Output displacement

图8 给出了粘滑定位平台的模态分析结果，前四阶固有频率分别为428.7，442.5，1 286.2，2 051.5 Hz。定位平台沿x，y方向的共振频率几乎相同，且频率较高。因此，平台具有良好的动态性能。此外，定位平台刚度的有限元仿真值和理论计算值如表2 所示。理论值与仿真值虽存在一定误差，但基本吻合，说明了计算模型的合理性。

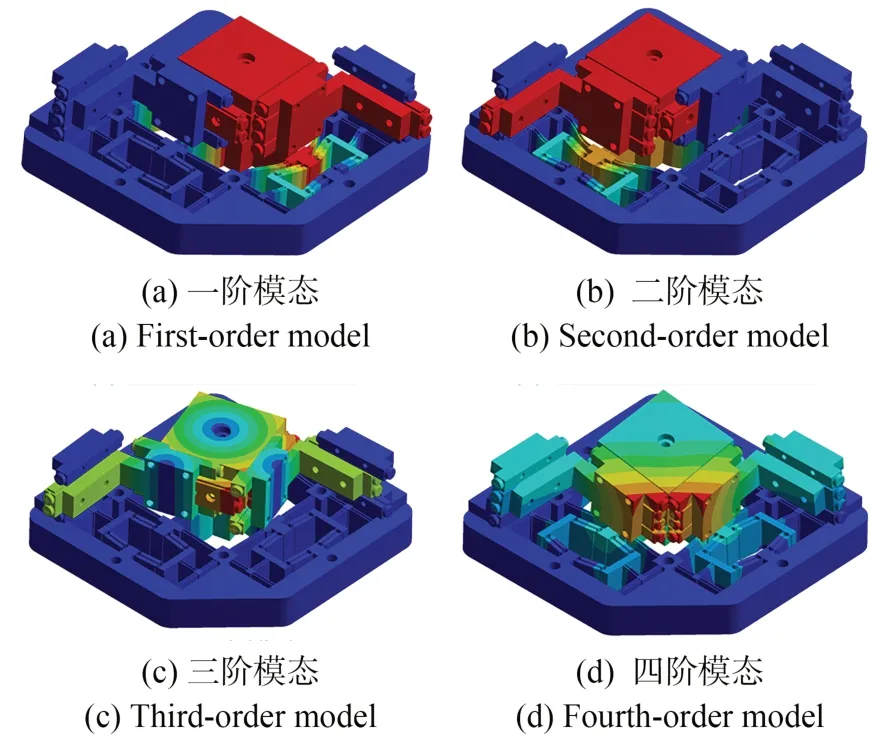
图8 粘滑定位平台的前四阶模态Fig.8 First four modes of stick-slip positioning platform

5 测试实验与结果

5.1 实验测试系统

图9 给出了粘滑定位平台的实验测试系统。驱动机构采用7075 铝合金并通过线切割加工而成。两对交叉滚柱导轨（日本THK，CRWM1-20）通过连接件垂直安装，用于引导移动台运动。工控机通过数据采集卡（美国国家仪器，NI-9263）发送驱动电压信号，该信号经电压驱动电源（哈尔滨芯明天，E01.C3）放大，作用于压电驱动器（哈尔滨芯明天，PSt 150/5×5/20），推动样机运动。平台输出位移由高精度激光位移传感器或电容传感器检测，并通过传感器控制模块传入计算机。

图9 粘滑定位平台实验装置Fig.9 Experimental setup of stick-slip positioning platform

5.2 扫描驱动模式下输出位移测试

对x和y向施加幅值150 V、频率1 Hz 的正弦驱动电压，定位平台在x和y方向的输出曲线如图10 所示。图中，Dx为x向输出位移，Dy为y向输出位移，Dc为耦合位移。x和y向的最大位移分别为63.84 μm 和62.61 μm。此外，图10 也给出了定位平台平动运动时的耦合位移曲线。当定位平台沿着x方向运动时，最大耦合位移为0.33 μm，耦合比为0.52%；y方向运动时的最大耦合位移为0.37 μm，耦合比为0.59%，因此定位平台具有良好的解耦性能。

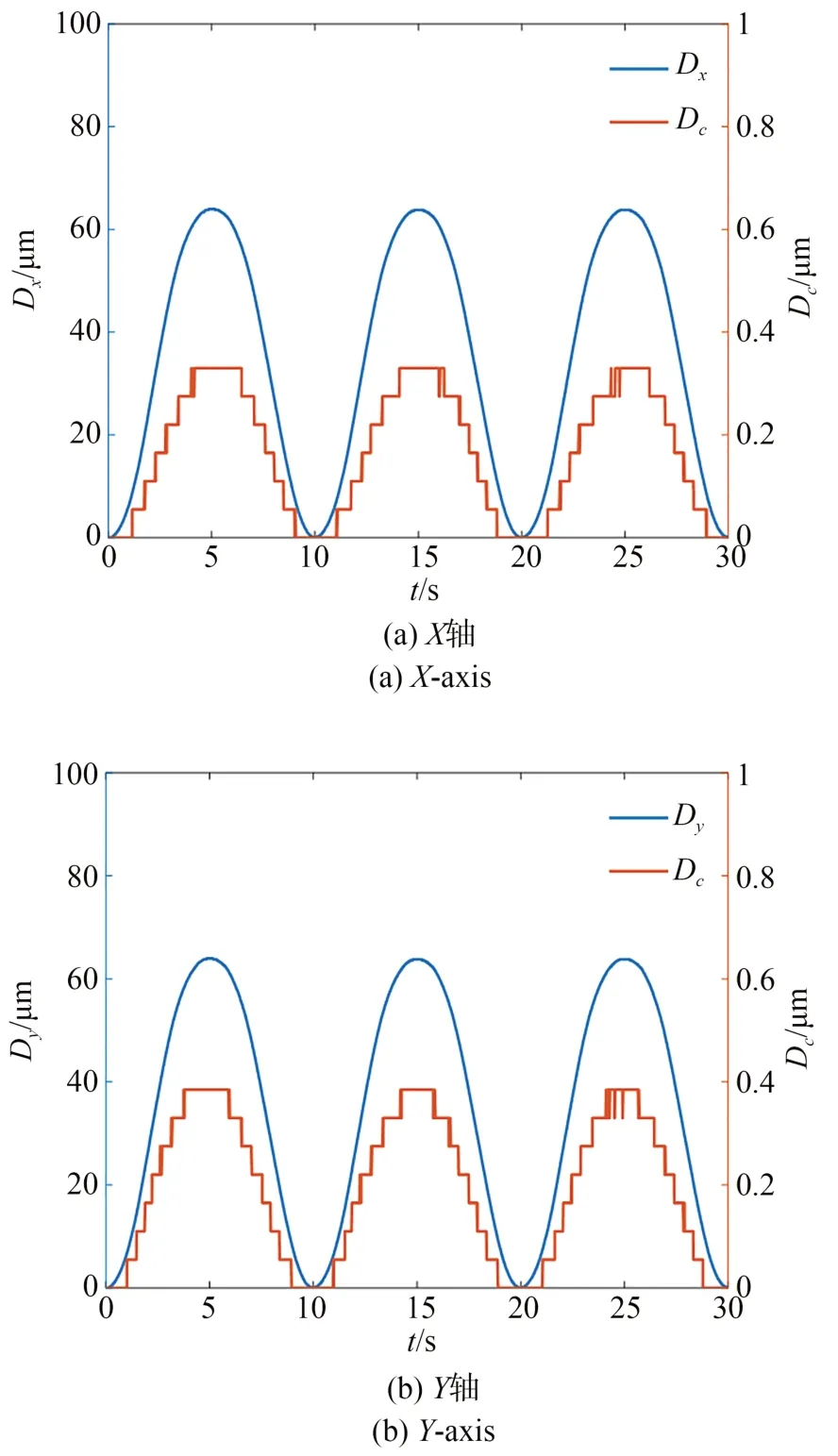
图10 输出位移Fig.10 Output displacement

5.3 步进驱动模式下运动位移测试

当1 Hz 锯齿波电压从0 V 间隔30 V 升高至120 V 时，平台输出位移如图11 所示。如图可知，输出位移随电压升高逐渐增大。x和y向输出近似，两个运动方向的粘滑特性类似。电压为120 V 时，x向最大单步位移S1为47.31 μm，有效单步位移ΔS为38.90 μm，耦合比为0.69%。类似地，y向最大单步位移S1为47.20 μm，有效单步位移ΔS为37.45 μm，耦合比为0.73%。因此，粘滑平台在大范围行程下依然具有良好的解耦性能。

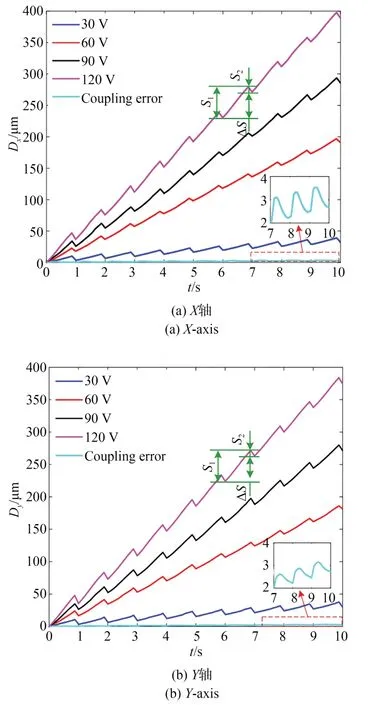
图11 粘滑位移Fig.11 Stick-slip displacement

5.4 运动速度测试

在120 V 锯齿波驱动电压作用下，定位平台运动速度与驱动电压频率的关系曲线如图12 所示。随着驱动频率的增大，平台运动速度先增加后减小。这是因为低频时平台的单步有效位移变化较小，运动速度会随着频率的增加而上升。但由于定位平台带宽有限，当频率超过带宽时，单步的有效位移显著减小。因此，在达到最大输出速度后，虽然驱动电压频率不断增加，但位移会以更快的趋势减小，导致定位平台运动速度不断下降，这与高频段实验结果一致。所以，定位平台的最大运动速度发生在350 Hz 左右，为13.40 mm/s。

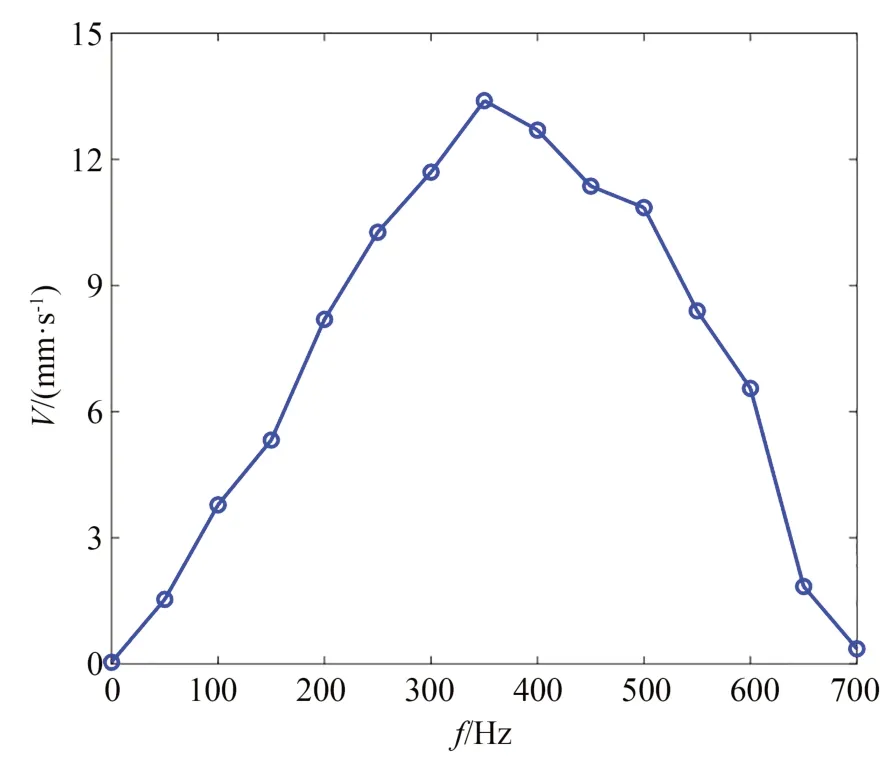
图12 不同频率下的运动速度Fig.12 Motion velocity with different driving frequencies

另一方面，随着驱动电压频率的不断增大，锯齿波激励可能会带来更为复杂的振动波形，影响粘滑运动。同时，压电驱动器也会发热，导轨之间也存在快速摩擦磨损现象。因此，压电粘滑平台在实际应用时，其驱动电压频率一般远小于共振频率，以保证粘滑运动性能。

5.5 垂直负载能力测试

定位平台的垂直负载能力是评价平台输出性能的重要指标。这里通过增减砝码测试了定位平台不同垂直负载下的输出位移变化曲线，如图13 所示。测试时，保持锯齿波驱动电压为 120 V，频率为1 Hz。由图13 可知，当负载在0 ～ 7.5 N 内，有效单步位移基本不变，约为38.5 μm，说明施加7.5 N 载重时，定位平台依然具有稳定的输出性能；而当承载力大于7.5 N 时，单步位移随着载重的增大而逐渐减小，最大垂直负载能力为50 N。

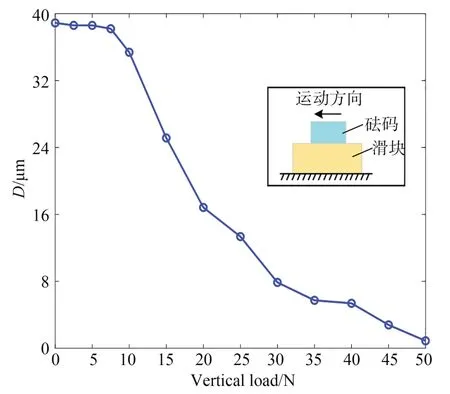
图13 单步位移与垂直负载的关系曲线Fig.13 Relationship between step displacement and vertical load

5.6 位移分辨率测试

图14 给出了定位平台在台阶电压驱动信号下的位移分辨率。测试时台阶信号间隔周期为1 s，通过不断调整驱动电压幅值，在幅值为0.1 V 时，对定位平台两个运动自由度进行测试。由图14 可知，扫描驱动模式下x向分辨率为6.5 nm，y向分辨率为7.2 nm，定位平台具有良好的位移分辨率。

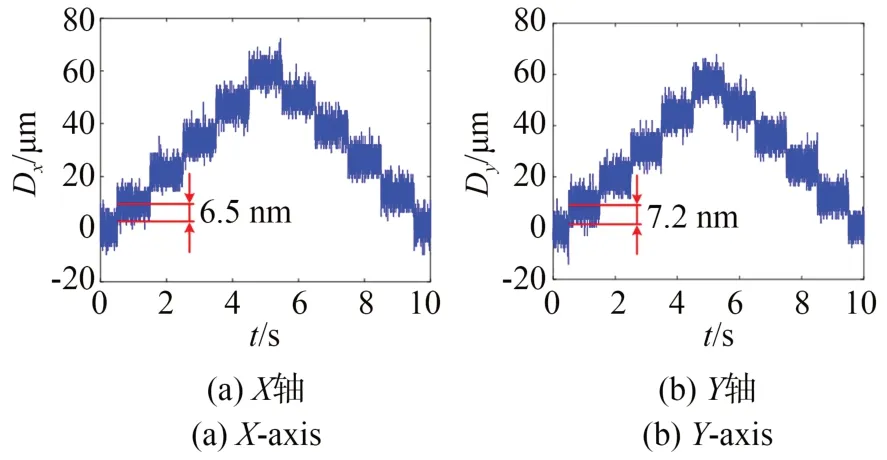
图14 扫描驱动模式的位移分辨率Fig.14 Displacement resolution for scanning driving mode

图15 给出了定位平台在锯齿波电压驱动信号下的位移分辨率。在步进驱动模式下，将驱动频率固定在1 Hz，并不断减小驱动电压幅值。驱动电压幅值为5 V，即为最小启动电压。由图15可知，x正向、x反向、y正向和y反向的运动分辨率分别为0.49，0.47，0.47 和0.42 μm。

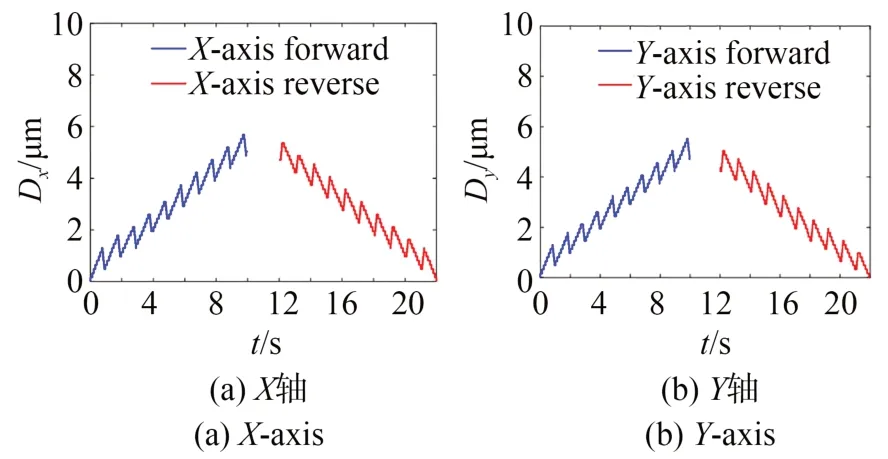
图15 步进驱动模式的位移分辨率Fig.15 Displacement resolution for stepping driving mode

6 结 论

本文介绍了一种新型的二自由度大行程无耦合压电粘滑定位平台的设计、建模和实验测试。首先，利用有限元法分析了定位平台的输出位移和刚度特性。然后，采用ANSYS Workbench 对定位平台的位移放大比和固有频率进行仿真。最后经过实验测试，验证了定位平台的输出性能及运动性能。在扫描驱动模式下，驱动电压为150 V 时，x和y向的输出位移分别为63.84 μm 和62.61 μm，耦 合 比 为0.52% 和0.59%，分辨率为6.5 nm 和7.2 nm。两个方向具有类似的运动性能。在步进驱动模式下，驱动电压为120 V 时，平台在x和y向的单步位移分别为47.31 μm 和47.20 μm，耦合比为0.69%和0.73%，x正向、x反向、y正向和y反向的运动分辨率分别为0.49，0.47，0.47 和0.42 μm。锯齿波驱动电压为120 V，频率为350 Hz 时，定位平台达到最高运动速度，为13.40 mm/s，定位平台的最大垂直负载能力为50 N，适用于众多微纳操作场合。