空间最优投影平面的斜口圆截面管路端头位姿测量

尚国威， 梁 晋*， 李磊刚， 牌文延， 赵贵中

（1.西安交通大学 机械工程学院 机械制造系统工程国家重点实验室，陕西 西安 710049；2.新拓三维技术（深圳）有限公司 创新实验室， 广东 深圳 518060）

1 引 言

管路在船舶、汽车、航天等工业领域扮演着重要角色，负责液体或气体的运送和重要部件的连接。圆形截面弯管受力均匀，制作工艺方便，在实际装配过程中通常采用圆形截面弯管进行连接。汽车、船舶、飞机等工业产品在运行过程中，不可避免地会产生振动，管路的受力更为复杂，管路焊接处为管路系统中受力较大的部分，一旦超过临界水平的应力累积时间过长，会引起疲劳裂纹的出现［1］，造成管路连接处断裂，对管路系统寿命造成巨大影响。目前，工程中管路通常由数控弯管机对圆柱形管路弯曲加工制得，在制作完成后对端面进行切割，通常弯管端面垂直于轴线进行切割。近年来，由于船舶、飞机等发动机越来越倾向于小型化，占用空间减少，对于此类比较狭窄空间的管路，用弯管连接会导致管路弧度太大，空间不够；如果用弯头连接，管路两条焊缝之间的距离太短，会影响质量。在此背景下，斜切截面被提出，通过将斜切面的中心进行对齐焊接，减小占用空间，如何进行管路端点位姿的精确测量，提高焊接对齐精度，减小应力集中，是管路端头测量过程中最重要的一环。

传统管型测量方法通常为靠模法或激光叉扫描点云测量方法，它们都存在测量精度不足，测量方法依赖人工操作，测量效率很低的缺点。近年来，以摄影测量为基础的立体视觉技术得到了快速发展，为弯管高效高精度的检测提供了新思路。它的特点是非接触、使用便捷、高效、准确、不受人工影响，因此广泛应用在工件质量检测、自动化装配等工业场景［2］。国内外学者在管线重建与测量上进行了大量研究［3-7］，这些方法直接以管线末端点作为端点，测量得到的管路端点精度较低。由于此类方法提取的轴线为图像中心线的三维重构，当端口出现倾斜时，中心线提取精度较低，因此要求测量的管路端头为平口，即端面与轴线垂直，无法测量斜口管的端点。单独针对端点测量的研究较少，主要通过拟合末端圆弧，在二维图像上测量弯管端点，再通过三维重建测量得到端点坐标。张天等［8］利用管路末端圆弧中点与中心线端点距离最近的性质得到管路末端圆弧，并用最小二乘法拟合椭圆，得到端点图像坐标。娄群等［9］根据局部区域面积效应估计非连续性边缘模型的二阶边缘参数，提高椭圆中心的拟合精度。陶立民等［10］通过欧式距离作为阈值删除噪点提高椭圆拟合精度。贾棋等［11］基于二次曲线约束的两阶段弧过滤策略对图像中椭圆边缘点进行筛选，提高椭圆拟合精度。王健等［12］利用多视角拍摄弯管提取管路轴线，通过中心线向量与管路外径测量端点的图像坐标。金鹏等［13］通过统计管路直径像素值，沿管线方向移动，在像素值发生变化点认为是管路端点坐标，还设计了二维靶标用于测量管路端点。张继耀［15］通过边缘轮廓约束拟合空间圆，直接对端点进行三维测量。

以上研究都只考虑了管路端面中心点的精确测量，实际安装过程中由于管路体积较大，通常使用机械臂输入位置参数进行装配，此过程中不仅依赖管路端面中心点，还依赖于端面的法向量以及与另一端管路端面中心点位置和法线关系的相对关系，它们共同决定了管路的装配质量。因此，还需研究一种管路端头测量方法，不仅能够测量管路中心点的相对位置，还能精确测量端面法向量。

针对斜口管路端头的位姿测量问题，本文采用多目立体视觉重建高精度管路轴线及末端面，通过非线性寻优得到残差最小的空间椭圆，重建得到空间椭圆中心以及端面与轴线夹角作为管路端头的位姿测量结果。实验结果表明，该方法能够准确计算管路端头位姿，满足精度要求且计算效率较高。

2 测量模型及基本流程

空间最优投影平面的端头位姿测量方法的具体流程如图1 所示。

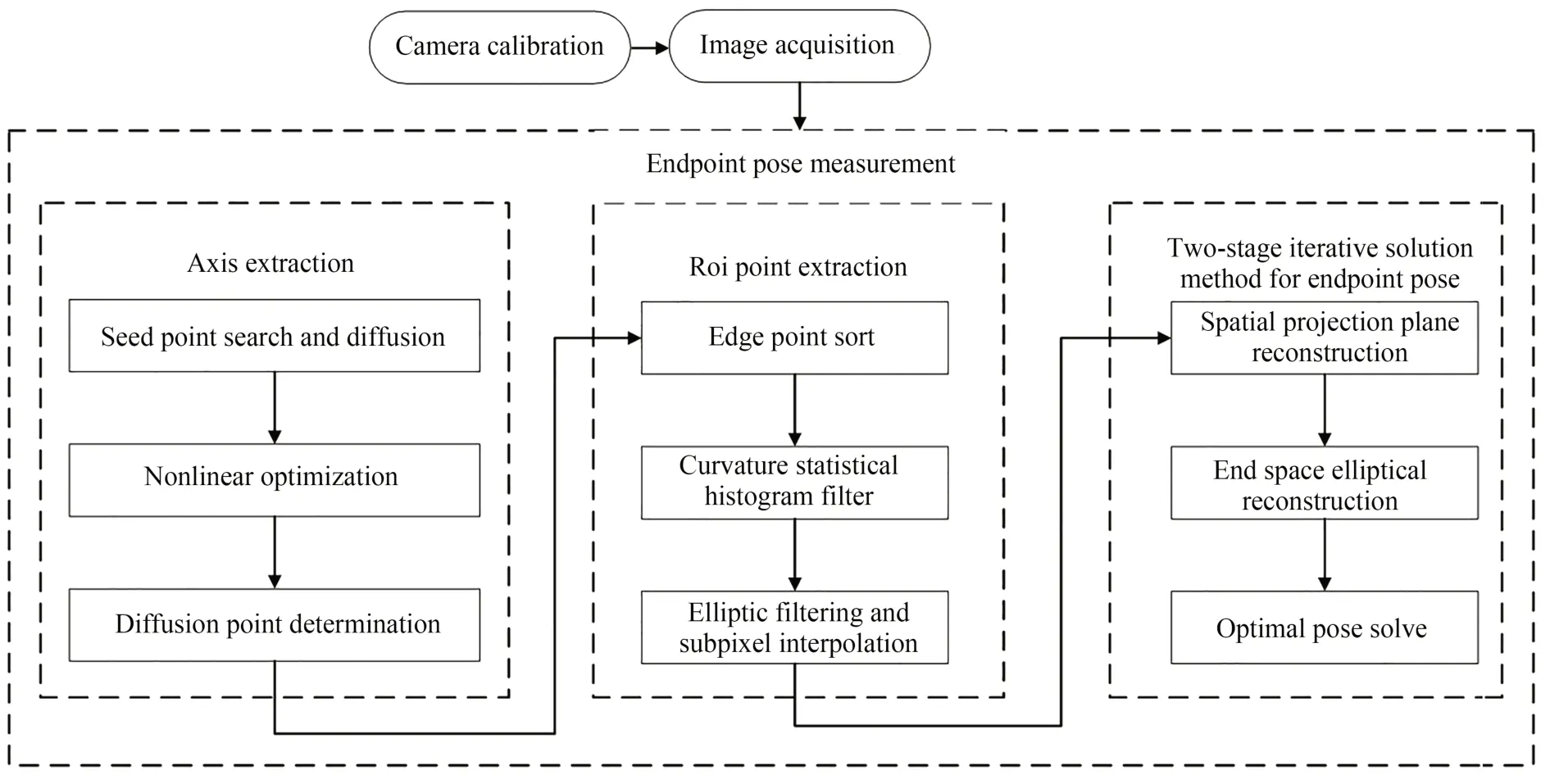
图1 端点位姿测量流程Fig.1 Flow chart of endpoint pose measurement

2.1 相机标定

通过摄影测量十参数相机自标定方法对相机进行标定，控制相机抓取管路图像。

2.2 管路轴线重建及终止点设置

忽略斜口管端头处特征，将整个弯管视为首尾相连的小圆柱，从弯管多视角图像上选取较优的种子圆柱段（靠近测量区域中心的直线段区域），结合本文提出的非线性寻优方法提高种子圆柱的重建精度，并利用极线约束找到它在每个视角下的对应圆柱段，利用多视几何的理论重建管路轴线，以种子圆柱为起点进行双向扩散，扩散过程中一旦拟合圆柱半径变化超出阈值即停止圆柱扩散。

2.3 基于特征的端面点筛选

通过边缘提取得到的像素点坐标进行八邻域排序，将排序后临近点建立曲率特征直方图，结合曲率特征图筛选方法以及椭圆拟合滤波及亚像素插值得到端面特征点参与后续优化计算。

2.4 端点位姿求解

通过端面特征点结合管路圆柱模型重建管路端面，分步修正端面及端面形状重建得到残差最小的空间椭圆。空间椭圆中心即为管路端点，空间椭圆所在平面与轴线的夹角即为端头位姿。

2.5 斜口管数学模型

在空间表达上［16］，末端无附件的正口弯管件可以看作由细长圆柱体在一定折弯角度下折弯得到的空间形态规则的物体，末端小圆柱与倾斜平面相交形成斜口管端头，如图2 所示。其空间形态可以使用弯管轴线，弯管折弯半径以及末端面法向量来表达，其中弯管端点由管路轴线与端面交点表示。

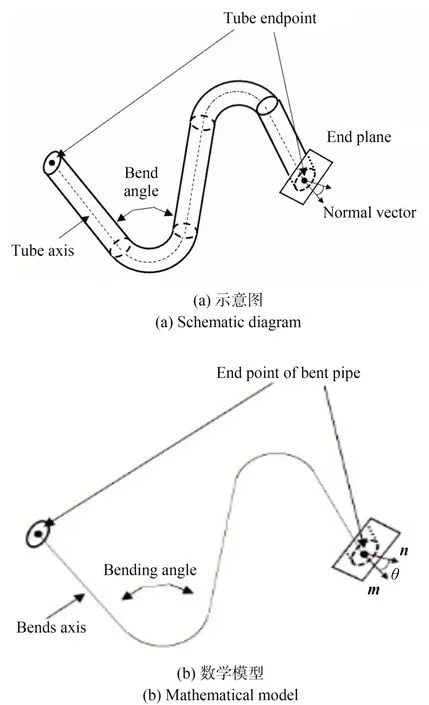
图2 斜口管三维形态描述Fig.2 Three-dimensional morphological description of oblique mouth tube

根据空间立体几何得到管路端头处的角度为：

式中：m为末端轴线的方向向量，n为末端面法向量。

3 测量原理

3.1 相机标定

图像在工业相机上的成像是一个光学成像过程，主要涉及4 个坐标系（像素坐标系、图像坐标系、相机坐标系和世界坐标系）之间的转换，通常采用小孔成像模型为理想成像模型。如图3 所示，相机的光心为O，所有的入射光线均经过该点，理想图像主点Oc为图像的几何中心点，过相机光心O与图像主点Oc的直线为相机光轴，物方点Pw在像平面上的理想像点为P，光心与图像主点之间的距离为相机的焦距f。

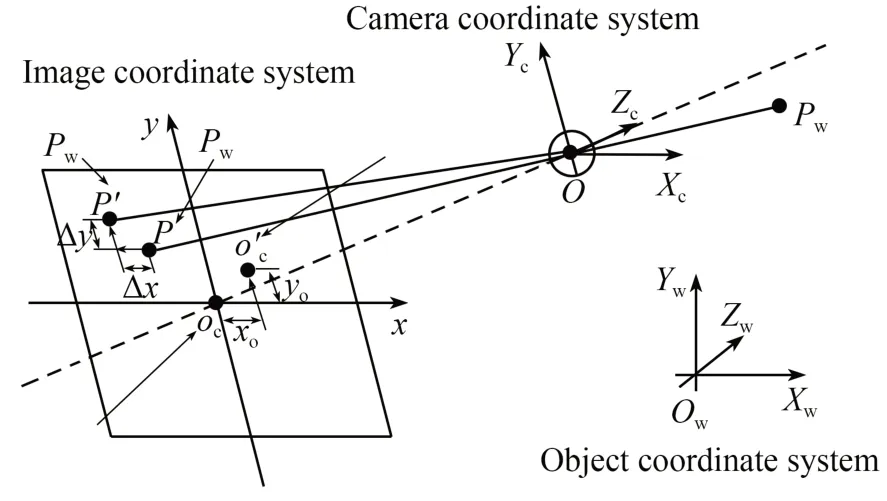
图3 相机成像模型Fig.3 Camera imaging model

由于工业相机及镜头实际的加工生产及装配过程中存在误差，图像主点会存在偏移，成像平面也不能保证垂直于相机的光轴方向，从而导致实际成像过程与理想的小孔成像模型之间存在偏差，即图像存在畸变，如物方点Pw在像平面上的理想像点P与实际像点P'之间存在偏差。考虑到实际成像过程中存在图像畸变，可以得到摄影测量中的共线方程：

式中：(x，y)为物方点在像平面的成像坐标；(x0，y0)为像平面中心；(Δx0，Δy0)为物方点对应的像点畸变量；(Xw，Yw，Zw)为物方点在世界坐标系下的坐标；f为镜头焦距；(Xs，Ys，Zs)为光心在 世 界 坐 标 系 下 的 坐 标；a1，a2，a3，b1，b2，b3，c1，c2，c3为世界坐标系到相机坐标系的旋转矩阵中的元素。

测量系统标定时，将标定板置于测量系统背光板上，并预先设定好标定板的14 个姿态，10 个相机同时采集标定板每个位姿的图像，用于后续的计算。标定板由编码点和非编码点组成，如图4 所示。

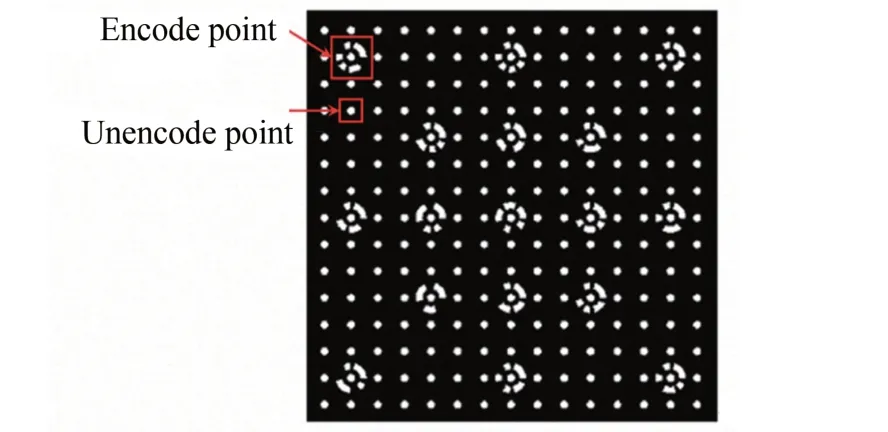
图4 标定板图像Fig.4 Image of calibration plate

通过已知的编码点与全局点的对应关系得到所有点与三维全局点的关系，结合共线方程计算得到相机内外参数完成相机标定。

标定板尺寸应与测量幅面一致，才能保证测量范围内的测量精度达标，标定板尺寸为120 mm×80 mm，能够满足在管径为10～200 mm 的弯管在测量幅面内的高精度测量。

3.2 管路轴线提取及终止点设置算法

3.2.1 管路轴线提取算法

为了进行高精度管线重建［3］，将多视角采集到的所有图像，通过最小二乘法结合边缘提取算法定位图像中直线区域，再通过高精度的直线拟合提高圆柱拟合的精度。重建误差最小的管单元称为种子圆柱段，通过立体视觉匹配选择种子圆柱段，具体要求为：（1）区域的边界为梯度方向的最大灰度值；（2）如式（2）和式（3）所示，边缘点拟合管件两侧直线度及平行度满足阈值；（3）满足上述两个条件的种子点可以在两张以上的图像中搜索到。

如图5 所示，在完成种子圆柱段搜索后，通过极线搜索匹配对应边缘点，通过重建得到的种子圆柱边缘点进行圆柱拟合，获得种子圆柱段的圆柱半径以及圆柱中心点。

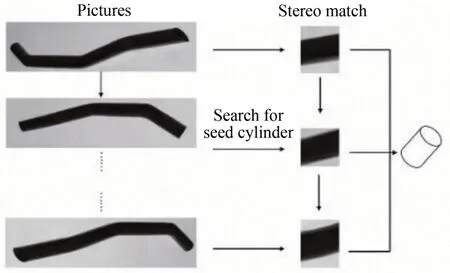
图5 种子圆柱拟合Fig.5 Seed cylindrical fitting

为进一步提高管路空间轴线的拟合精度，在获得种子圆柱参数后，结合边缘约束进一步对种子圆柱进行非线性寻优。相机成像模型如图6 所示，管路边缘点为相机光线与管面切点的二维投影，因此切线到轴线的异面直线距离为管路半径。

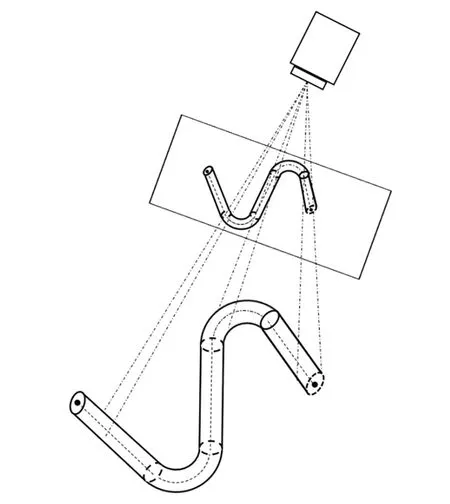
图6 管路成像示意图Fig.6 Schematic diagram of pipeline imaging

管路轴线的非线性优化过程如图7 所示。相机发射出的光束满足：

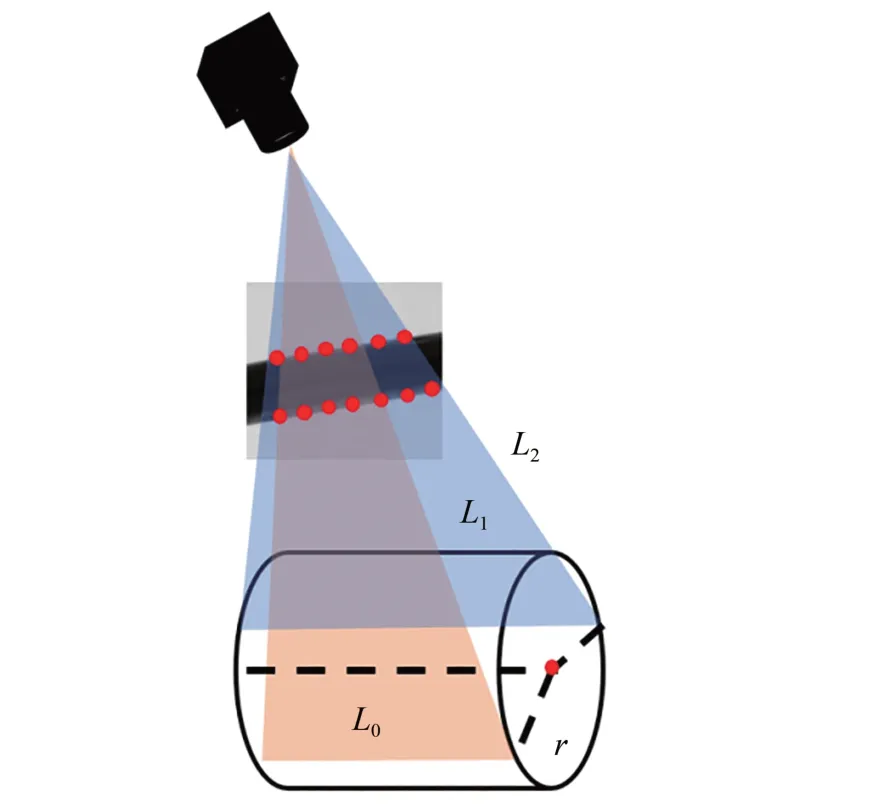
图7 种子圆柱轴线优化光线模型Fig.7 Model for seed cylindrical fitting

式中：Lij为第i个相机提取到的种子圆柱的边缘点对应的光线，r为初始拟合圆柱得到的圆柱半径，L0为拟合得到的圆柱轴线，r和L0为待优化变量，通过非线性优化圆柱轴线及半径得到高精度管路轴线。

在得到优化后的种子圆柱后，通过一定的步长沿着初始空间圆柱的轴线方向进行扩散，扩散后依然按照式（2）进行圆柱非线性寻优。扩散过程如图8 所示，通过圆柱的双向扩散，以扩散得到的圆柱中心点及方向拟合出弯管的空间轴线。

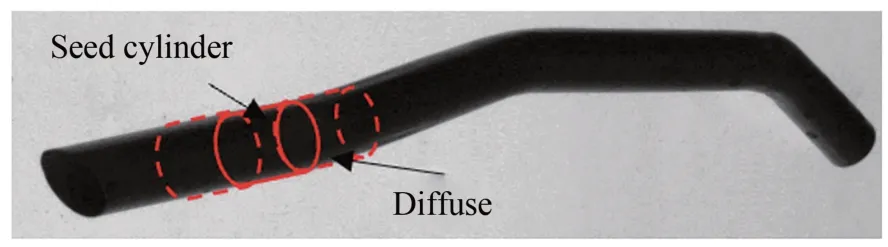
图8 圆柱扩散模型Fig.8 Cylindrical diffusion model

3.2.2 轴线终止点确认

如图9 所示，由于轴线提取过程中按照种子圆柱段基于边缘约束扩散进行拟合，在末端头会发生圆柱拟合异常，通常表现为圆柱半径变化较大，如小圆柱所示。

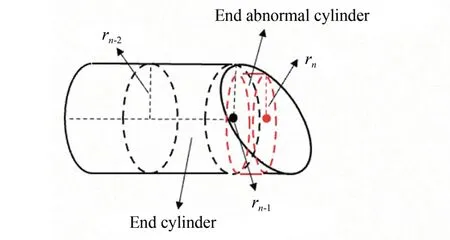
图9 末端圆柱扩散异常模型Fig.9 End cylindrical diffusion anomaly model

因此终止扩散条件设定如下：

式中：rn代表基于边缘轮廓约束扩散的第n个小圆柱的半径，tradius为相邻圆柱半径的偏差阈值。当半径波动超过阈值时，则认为扩散停止，取前一个小圆柱为末端圆柱。最终以扩散末端小圆柱的端点作为轴线末端点，圆柱轴线向量作为末端轴线向量。

3.3 端面边缘特征点提取算法

3.3.1 端面边缘轮廓点初始提取

末端面看作由平面与圆柱面相交而成，相交的截面形状如图10 所示。

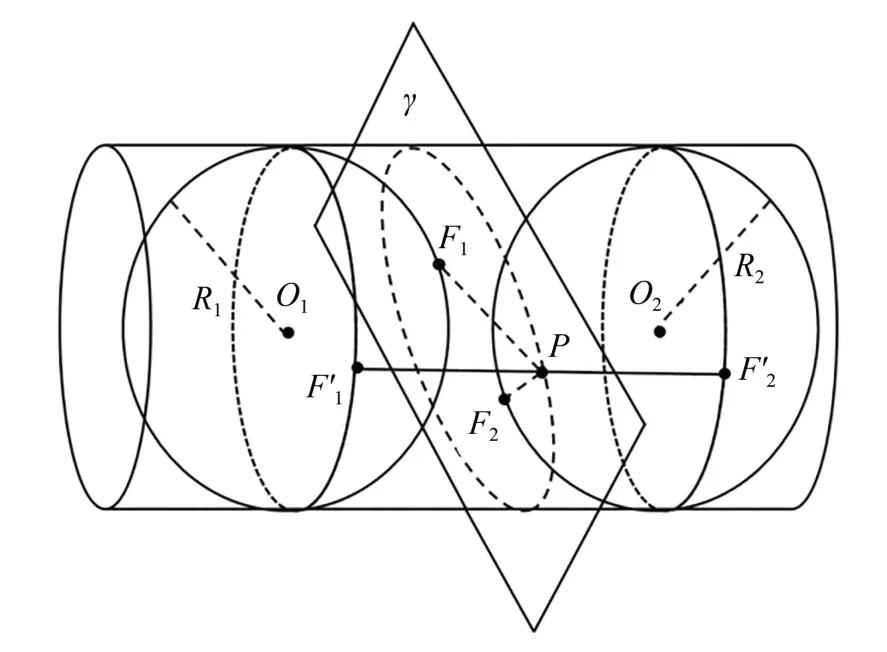
图10 双球数学模型Fig.10 Double-ball model

图中，虚线部分为γ平面与圆柱的截交线，为证明斜切面形状，将双球放入圆柱中，其半径与圆柱底面半径相同，双球与圆柱相切。假设 球O1，O2处 于 圆 柱 内 部，且 球O1与 平 面γ相切 于F1，球O2与 平面γ相切 于F2，取 截 口曲 线上任意一点P，由球的切线性质，即过同一点的球的切线长度相同，可以得到：

式中：F'1F'2为两个球与圆柱公共部分沿母线方向的距离，只要平面、球、圆柱的相对位置不变，则长度不变。因此，截面曲线上任意一点与切点F1，F2之和为定值。根据椭圆第一定义，截口曲线为以F1，F2为焦点的空间椭圆。由于圆柱面可以看作由无数个底面相同的圆组成，因此，截面椭圆的短轴长度为圆柱直径。

由相机成像模型可知，相机光轴与管路端面法线不垂直时，端面在摄像机中的投影在相机不垂直于轴线方向时为椭圆。多目视觉测量系统由于采用多相机进行拍摄，很好地避免了这种情况。如图11 所示，相机不是垂直投影，实际空间中的椭圆中心与二维图像椭圆中心由于透视投影偏差［17-18］并不重合，本文针对这一问题，采用拟合空间椭圆的方式直接得到三维中心，大幅提高测量精度，同时也能对端面角度进行测量。

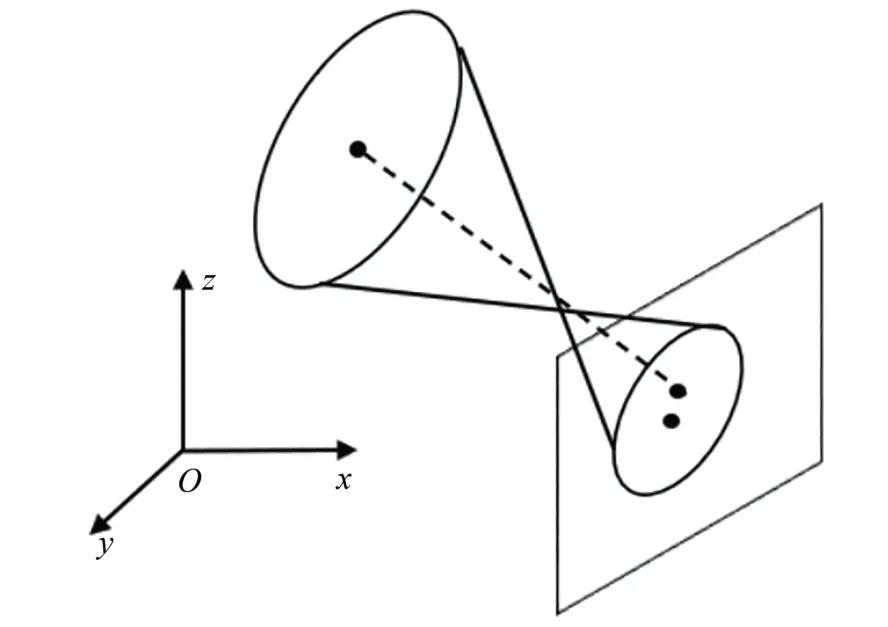
图11 透视投影偏差模型Fig.11 Perspective projection bias model

首先，通过边缘提取算法提取每个视角拍摄的管路整像素边缘坐标，将每张图像得到的坐标按照次序放入不同线性表有序排列，线性表首坐标为边缘点像素横坐标最小点（即x坐标最小点）。按照领域中右上方坐标开始，顺时针进行搜索，搜索到边缘点则停止，在搜索到的坐标按照八领域进行搜索，最终将边缘点整像素坐标依次放入线性表，如图12（a）所示，将所有坐标按照指定顺序进行排序。

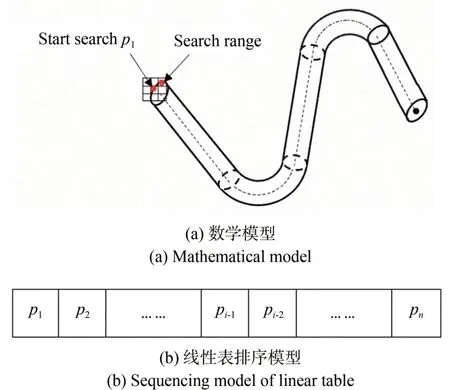
图12 边缘点次序排列示意图Fig.12 Schematic diagram of edge point order

端面特征点坐标获取方法如图13 所示。以一个视角为例，在获取到末端小圆柱端点坐标后，结合相机标定模型，将末端小圆柱端点投影回图像。分析管路形状特征可知，管路边缘为直线基元，管路端面边缘为曲线基元，因此，首先将特征点范围限制在末端点一定距离范围内，如图13 中虚线区域所示。由于曲率通常针对连续曲线，为统计离散点曲率，本文通过相邻三点拟合二次曲线，由二次曲线的曲率作为估计的边缘点曲率。

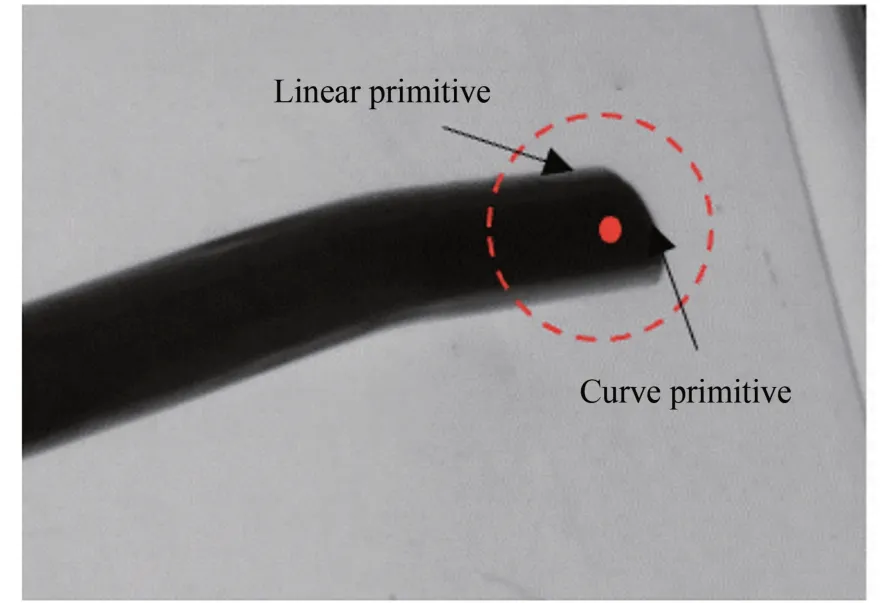
图13 弯管端面边缘提取Fig.13 Edge extraction of elbow end face

端面边缘点的筛选区域可被限制在末端点区域内，筛选区域表示为：

式中：（xend，yend）为末端小圆柱投影回图像坐标，（xi，yi）为线性表中第i个坐标，tdistance为设置距离阈值。

末端点区域内每3 个点具体的拟合曲线方程如下：

由拟合曲线方程以及连续曲线的曲率公式可以得到离散点的曲率计算公式为：

边缘提取过程中容易引入噪点，这是因为边缘提取算法对光源敏感，直线得到的像素坐标无法拟合成为完美的直线，曲率在直线段不完全为0，需要通过设置低曲率阈值进行筛选。

为区分弯曲段与直线段采用建立曲率统计直方图方式结合阈值筛选过滤区分直线段和曲线段，并且根据特征分析，曲线段中可能有一段平滑区域，将波峰之间的点全部当作端头边缘点，会使得统计点更为完整，仅仅设置阈值进行区分，则端头边缘处较平滑的部分就会被忽略，如图14 所示。满足筛选件的坐标作为端面坐标点提取的初始值。

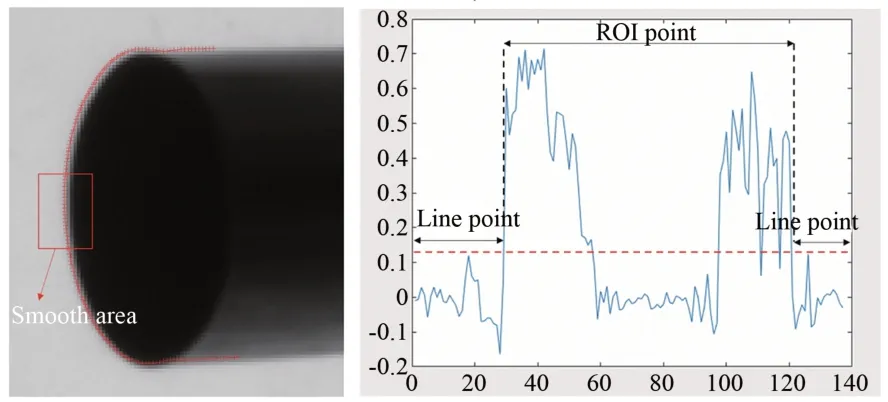
图14 特征点曲率统计Fig.14 Statistics of characteristic point curvature

3.3.2 端面边缘轮廓点滤波及亚像素坐标提取

考虑到通过曲率筛选的点仅是对端面点与端面附近边缘点进行筛选，并未过滤掉边缘提取过程中引入的噪声点，为了获得更精确的特征点，本文通过端面椭圆拟合剔除边缘提取过程中的噪点，具体算法流程如图15 所示。

图15 椭圆滤波算法流程Fig.15 Flow chart of elliptic filtering algorithm

首先，使用轮廓特征点初始值提取方法获得端面边缘点，将特征点通过最小二乘进行初始椭圆拟合，并进行标准化获得椭圆的中心点坐标、半长轴长度、半短轴长度和长轴与轴夹角。利用这些标准化参数，将边缘点坐标转换到椭圆标准方程坐标系下，即椭圆长轴与轴夹角为0，椭圆中心点坐标为（0，0），转换后的端面边缘点坐标为：

进一步，利用标准坐标系下的椭圆计算拟合椭圆的标准差，得到：

式中a，b为拟合椭圆的长轴与短轴。

利用3σ原则对端面边缘点进行滤波，即满足条件式（11）的端面边缘点保留，不满足则剔除；获得新的端面边缘点坐标后，重新进行椭圆拟合并以3σ原则剔除，直到所有的端面边缘点均满足原则时停止迭代，即点的数量不再发生变化时停止迭代。

此时剩余的边缘点坐标即为后续参与空间投影平面迭代优化的端面边缘点坐标。由于背光板导致管路边缘出现反光，部分整像素提取边缘时会出现肉眼可见的偏差。如图16 所示，常用的临近点双线性插值方法提取亚像素边缘点，局部点的误差较大。针对这一问题，本文采用经过滤波后的边缘点进行全局最优的椭圆拟合，采用整体的整像素点估计亚像素点，能够避免局部点误差过大导致的亚像素点插值误差较大的问题。通过射线求交得到亚像素坐标如图16 中白点所示，以此来提高后续端点的位姿求解精度。

图16 亚像素坐标插值方法对比Fig.16 Comparison of subpixel coordinate interpolation methods

求交点过程如图17 所示，射线从椭圆中心发射，在轴线二维投影的顺时针30°到逆时针30°内进行射线求交。

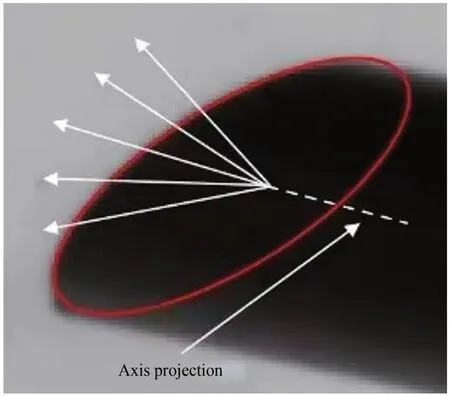
图17 亚像素坐标求解Fig.17 End face ellipse fitting

3.4 投影平面重建算法

在得到参与计算最优端面迭代优化的边缘点坐标后，通过摄影测量共线方程（式（12））以及相机标定模型，将得到的边缘点还原成空间光线，即：

式中：(x，y)为物方点在像平面给的成像坐标；(x0，y0)为像平面中心；(Δx0，Δy0)为物方点对应像点畸变量；(Xw，Yw，Zw)为物方点在世界坐标系下的坐标；f为镜头焦距；(Xs，Ys，Zs)为光心在世界坐标系下的坐标；a1，a2，a3，b1，b2，b3，c1，c2，c3为世界坐标系到相机坐标系的旋转矩阵中的元素。

由于图像上一点只能确定空间光线，无法获取到该点对应空间点的深度。为获取空间点深度，将平面视为空间中任意平面，由平面点法式表示，分析末端面特征可知，端面边缘点都位于圆柱表面。由圆柱模型特性可知：圆柱面上每一点到圆柱轴线的距离为圆柱半径，因此本算法的核心思想在于，通过非线性优化方法，使平面与圆柱表面交点到轴线的距离向圆柱半径逼近，得到的全局最优解即为最优平面，优化模型如图18所示。

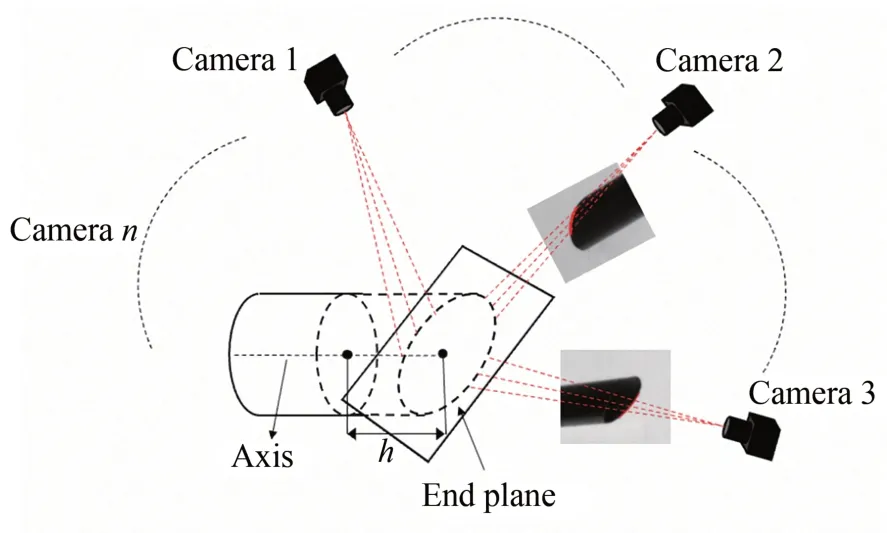
图18 最优端面重建算法模型Fig.18 Model of optimal end face reconstruction algorithm

最优平面可以表示为：

式中(vp1，vp2，vp3)为平面法向量，v0为末端圆柱轴线，h为沿轴线步长。

平面与光线交点可以表示为：

式中：（p1，p2，p3）为平面上一点；（l1，l2，l3）为光线上一点，因为光线必定通过相机光心，因此光线上一点即为光心在世界坐标系中的坐标；（vl1，vl2，vl3）为直线方向向量，由式（13）可得。因此，由式（14）可得不同相机发射的光线与平面的交点。

结合上文分析得到交点位于圆柱面表面构造优化方程，优化目标为光线与平面交点到轴线距离与弯管半径之差最小，构造的误差方程如下：

式中：ri为二维图像提取到的第i个亚像素边缘点形成光线与平面交点到轴线的距离，r0为弯管半径，N为筛选得到的边缘点数量。通过该优化方程可以很好地求解得到端面方程。

3.5 端点位姿分步优化算法

在得到初始测量端面后，端点位置初值认为是末端小圆柱的轴线与平面交线，切削角度为平面与末端小圆柱轴线的夹角。但由于末端轴线近似看作是末端小圆柱轴线，切割或轴线测量偏差可能会导致末端轴线与末端小圆柱轴线方向具有一定的偏差，因此，端点的精确值应当为轴线末端附近的全局最优值。通过前文分析末端面特征可知，末端面为椭圆面，在获取到最优平面后，相当于在空间中已知深度信息，所有边缘点可以在端面上进行重建。由于通过多相机采集相片，因此可以重建得到尽可能完整的端面边缘坐标，再通过空间椭圆拟合得到更精确的椭圆圆心。在得到椭圆圆心后，将椭圆圆心与最末端小圆柱圆心连线方向当作末端准确方向，椭圆圆心作为端点坐标。

为简化优化过程，采用先降维再拟合的方式进行椭圆拟合，如图19 所示。平面α为求解得到的初始端面，β平行于xoy平面，法向量为(0，0，1)，求得将平面α旋转到β的旋转矩阵，将α平面旋转至平行于xoy平面得到β平面，可以先不考虑z坐标的影响，直接在β平面进行椭圆拟合，然后再通过旋转矩阵将β平面坐标旋转回α平面，得到准确的空间点坐标。

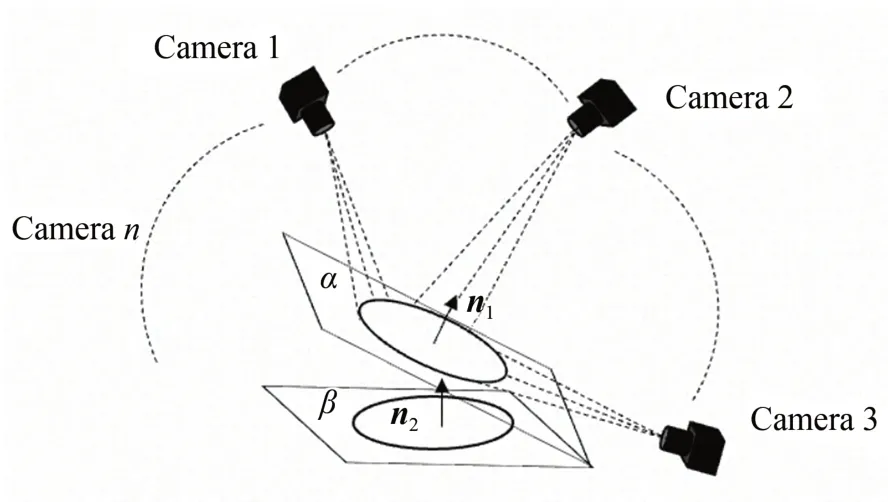
图19 椭圆降维拟合模型Fig.19 Ellipse dimensionality reduction fitting model

弯管端点的空间位姿优化问题为一个典型的非凸优化问题。若初值较差，则会导致优化过程收敛速度较慢或收敛于局部最优点，无法得到全局最优解，初值求解方法如图20 所示。

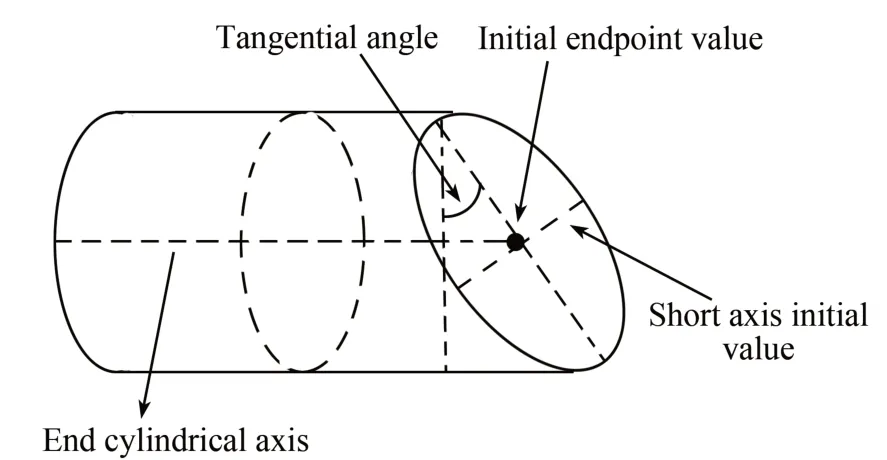
图20 椭圆初值求解方法Fig.20 Ellipse initial value solution method

椭圆圆心初值为轴线与平面的交点，椭圆短轴初值为弯管半径，椭圆长轴可以放在直角三角形中求得，即：

在获取到椭圆拟合初值后，为提高拟合精度，最小二乘拟合椭圆误差方程使用标准方程而非一般方程，误差方程为：

式中：(x0，y0)为待优化的椭圆圆心，a，b为椭圆的长轴和短轴。通过先修正端面，后修正端点，最终得到的末端点及末端面方程即为斜口管路端点的位姿测量结果。

最终得到的端点三维坐标投影回图像，如图21 所示，为放置于不同位置下端点的测量结果。

图21 端点测量结果Fig.21 Endpoint measurements results

4 测量实验与结果

4.1 实验平台

实验搭建的多目视觉测量平台如图22 所示。在该平台上进行管路测量实验，验证多目立体视觉下的斜口管路端点位姿测量精度。测量系统由10 个高精度相机（MV-CA030-10GM）、优质相机镜头（MVL-HF0628M-6MP）、LED 灯、背光板、遮光板、支撑架、控制盒和计算机（戴尔）构成。相机的像素分辨率为1 920×1 440，镜头焦距为6 mm，通过多目视觉保证管路特征尽可能被拍摄完整。

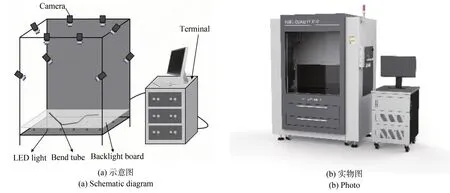
图22 多目视觉测量平台Fig.22 Multi-eye vision measurement platform

被测管件如图23 所示。为说明本方法的通用性，管件1 特征为：一端头为平口，一端头为斜口；管件2 特征为：两端头均为斜口。

图23 待测管件Fig.23 Shape of pipe to be measured

4.2 实验对比分析

管路端点的轴线精度可以通过两端点距离进行描述，管路端点位姿可以通过测量端头处的切割角度进行描述。上述管件经过三坐标测量机检测，得到的相对距离为管路一两端点距离为711.058 mm，端头1 处的测量角度为2.461°，端头2 处的测量角度为39.072°；管路二两端点的距离为211.715 mm，端头一处的测量角度为28.863°，端头二处的测量角度为117.598°，将三坐标测量仪得到的端点距离与端头位姿作为真值进行精度验证。

标定精度是测量系统精密测量的前提，因此，首先进行相机标定得到所有相机的重投影误差以及标定参数，以佐证本文视觉测量系统的精度，标定结果见表1。

表1 相机内参数Tab.1 Camera interior index

基于摄影测量的标定方法可以得到较高精度的标定结果，整体重投影误差低于0.03 个像素，满足高精度测量的要求。

在完成标定后，将待测管路放置在测量系统背光板上，并以任意角度摆放10 个不同的位置，拍摄不同位置下的管路图像，将端点之间的距离以及切削平面角度分别通过多目立体视觉进行测量，测量得到的端点位姿如表2 与表3 所示。

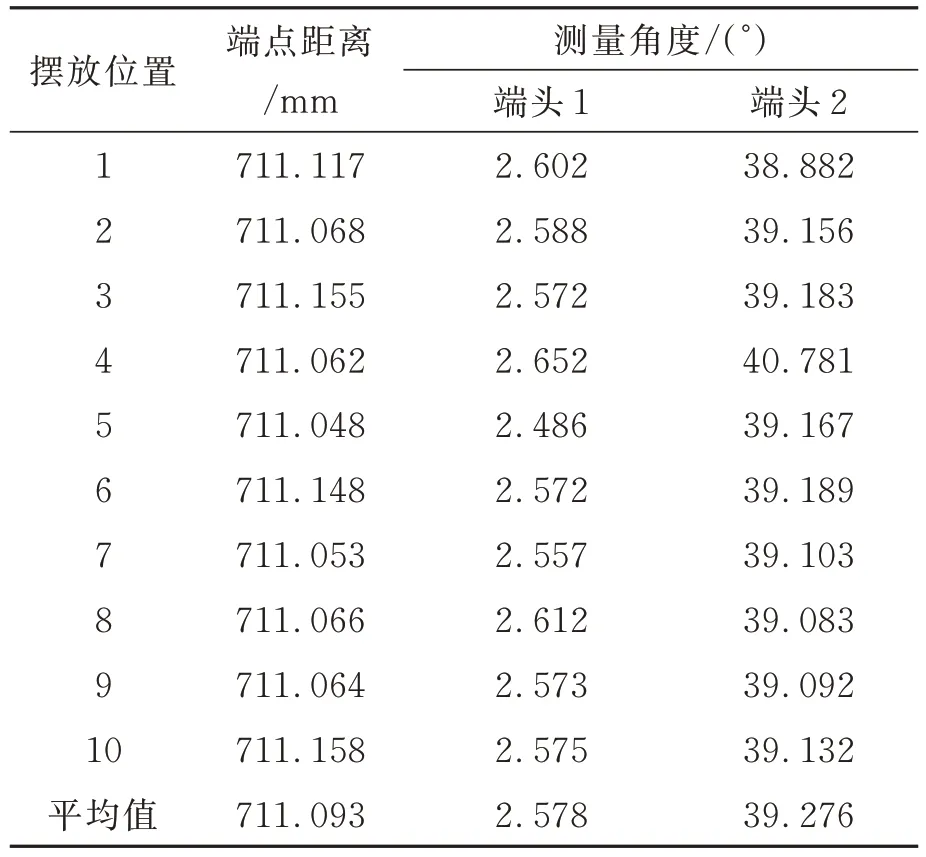
表2 管路1 的测量结果Tab.2 Measurement results of Pipe 1

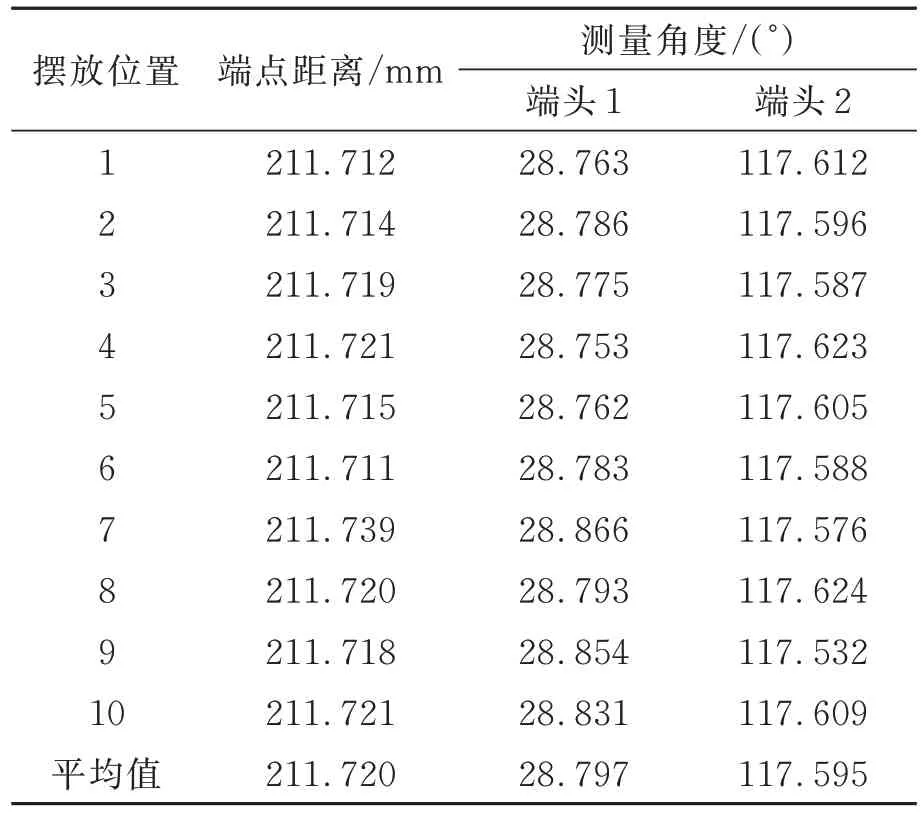
表3 管路2 的测量结果Tab.3 Measurement results of Pipe 2

光照分布不均的环境内，图像质量差［19］，因此亮度调节尤为重要。本文主要根据图像灰度直方图进行调节，过亮或过暗都会使得灰度直方图分布不均匀，如图24 所示，使测量精度受到影响［17］。为说明亮度对测量精度的影响，在低亮度及高亮度条件下进行了如图23 所示相同管路的测量，10 次重复测量得到的均值如表4 所示。

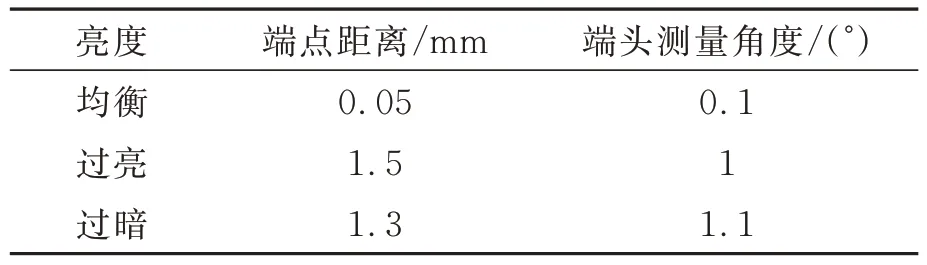
表4 不同亮度下的测量偏差Tab.4 Measurement mean at different brightness levels

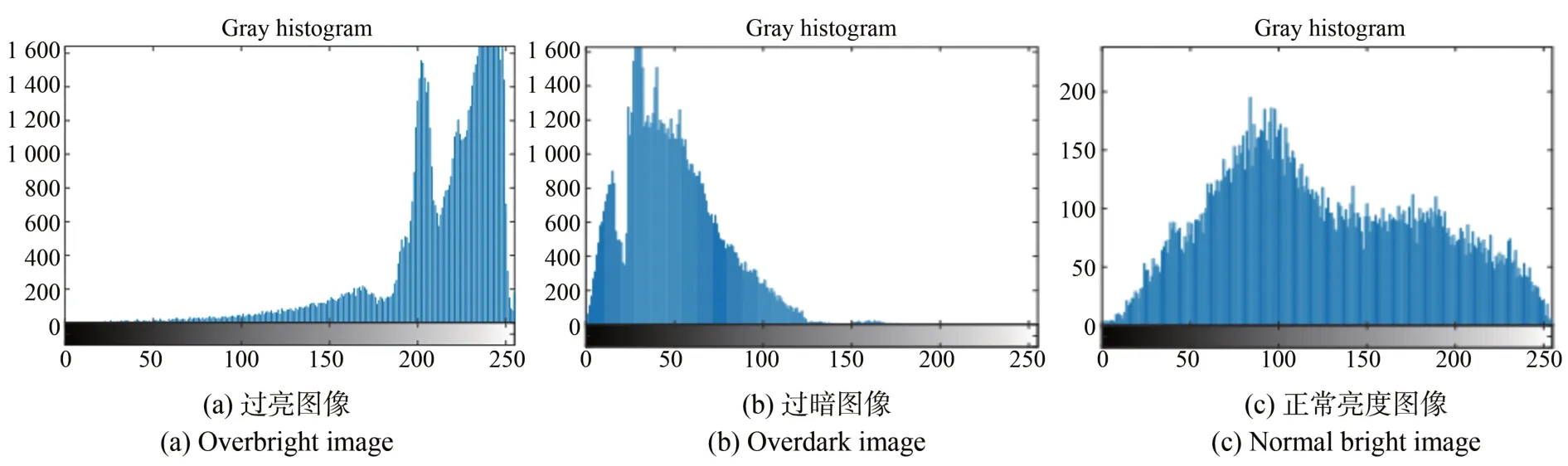
图24 不同亮度灰度直方统计图Fig.24 Grayscale histogram of different luminances

通过分析测量结果均值可以明显看出，光强对测量精度的影响较为明显，在光照过强或过弱时，距离测量误差超过1 mm，角度测量误差会超过1°。因此，实际中应该结合工程经验及灰度直方图分布对背光板光源进行调整。

由于目前暂时没有方法能够测量斜口管件端头的位姿，本文通过XTOM®面结构光扫描系统扫描管件进行管路端头位姿测量对比。分析端头处点云数据作为对比，管件1 的点云扫描结果如图25 所示。通过点云扫描端面拟合平面，扫描管路末端，拟合末端管路圆柱轴线，轴线与端面的交点作为管路端点，轴线法向量与平面法向量的夹角计算端头处角度，其余管件也按照本方法进行测量。面扫描针对管件端头测量结果如表5～表6 所示。

表5 点云测量管路1 的测量结果Tab.5 Point cloud measurement results of Pipe 1

表6 点云测量管路2 的测量结果Tab.6 Point cloud measurement results of Pipe 2

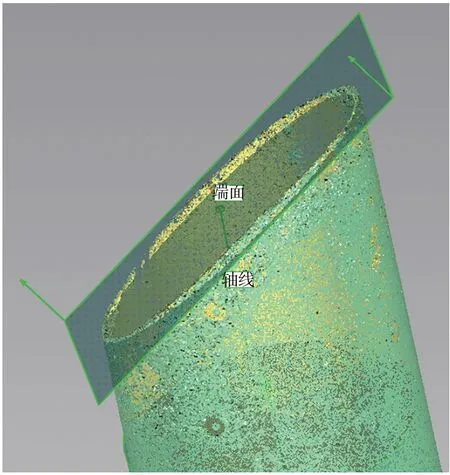
图25 点云端点测量示意图Fig.25 Point cloud of point measurement

4.3 测量结果对比分析

实验中，绝对精度定义为误差绝对值的最大值，重复精度定义为各个测量值间的最大偏差，检测精度对比如表7 和表8 所示。

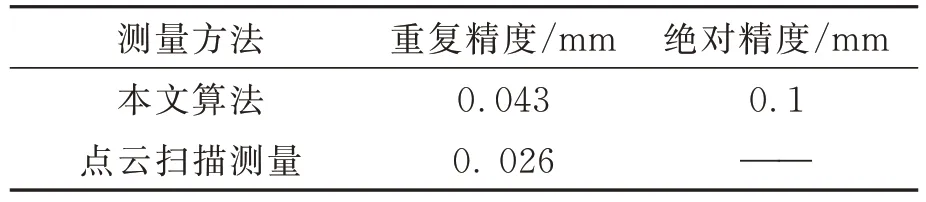
表7 端点距离测量精度对比Tab.7 Comparison of end-of-line distance measurement accuracy

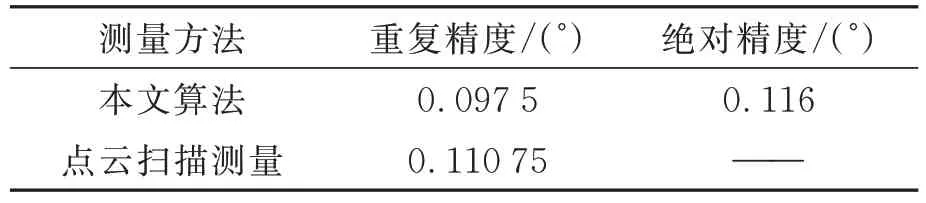
表8 端面切削角度测量精度对比Tab.8 Comparison of cutting angle measurement accuracy

由表7 可以看出，管路端点距离的重复测量精度为0.043 mm，较点云测量端点精度略低，但随着重复次数的增多，重复精度显著提高。点云扫描测量效率较低，并且由于引入人为操作，精度可能较差。

由表8 可以看出，整体角度测量的重复精度为0.097 5°，而点云扫描计算的重复测量精度为0.110 75°，误差略大，一定程度上验证本文方法具有较好的位姿测量精度。

为进一步验证本文算法的重复性，另外选取10 根直径包括φ30，φ40，φ50 mm 的管路零件，按照以上测量方式进行10 组重复测量，测量结果如表9 所示。

表9 不同测量方法的精度对比Tab.9 Comparison of measurement accuracy of different methods

为说明本文方法的优势，与已有的基于多目视觉的管路端点测量方法，如通过拟合末端轮廓线的端点测量方法［8］以及基于中心线的端点位置测量方法［14］进行对比，结果如表10 所示。

表10 不同视觉测量方法对比Tab.10 Comparison of different visual measurement methods

从表10 可以看出，传统的基于管路末端椭圆拟合的管路端点测量方法［8］与基于中心线的管路端点测量方法［14］的测量时间与精度较本文方法都有差距。此外，本文方法能够测量端点角度，在实际装配过程中具有更高的通用性和适用性。

通过对基于空间最优投影平面的管路端头位姿测量方法的实现流程进行分析，在测量系统标定结果良好的情况下，采用多目立体视觉的测量方法，其图像处理效果是决定端点位姿测量精度高低的主要因素。为了确保管路位姿测量结果的精确性，在筛选管路边缘点时，考虑到管路端面在成像过程中端面边缘点由曲线基元构成，管路边缘点为直线基元构成，通过双曲率阈值筛选以及椭圆拟合滤波得到最准确的端面边缘点坐标，为空间端面以及端点初值的计算提供了有力的保障。

为进一步提高端头位姿测量精度，通过分析端头投影回图像为椭圆，对边缘进行椭圆拟合，通过椭圆圆心发射射线，用交点作为管路边缘亚像素坐标替代传统的亚像素插值方法，能够很好地避免管路边缘处由背光板引起的反光而导致插值得到的亚像素坐标精度较低的问题。

与之前通过图像上搜索端点二维坐标再进行端点重建不同，本文提出方法结合弯管圆柱模型以及端面特征采用拟合空间残差最小的空间椭圆，以空间椭圆圆心作为端点坐标，有效地减小了多目测量系统中弯管端面处的空间椭圆投影回图像产生的透视投影偏差［20］，大幅提高了管路端点的测量精度。

基于空间最优投影平面的斜口管路端头位姿测量的测量误差进行分析，得到影响管路测量精度的因素主要有：

（1）管路截面加工质量。本文提出的测量方法通过重建管路端面进而进行管路端点位姿测量。然而，在实际的管路切割过程中，由于加工粗糙或材料本身较软，端面平面度较低，造成该方法测量精度下降。当管路端面的平面度较差时，可以通过精修管路端面来提高管路的测量精度。

（2）管路边缘的提取效果。由于管路最优端面的重建以及管路轴线的提取要在边缘提取的基础上进行，因此，每次图像边缘提取的质量直接影响管路轴线的重建以及管路端面的重建精度。而边缘提取效果主要受光源亮度的影响，为了保证每次开机测量时系统测量精度的稳定性，测量前要将背光板光源调到同一水平，具体可以参考采集图片中管路与光源的敏感对比程度。

5 结 论

本文针对已有的斜口圆截面管路测量方法精度不足以及无法兼顾端头位姿测量的问题，提出了一种基于空间最优投影平面的管路端头位姿测量方法。该方法通过直接重建空间椭圆避免透视投影偏差，大幅提高测量精度，同时能够兼顾端头位姿的高精度测量。与三坐标测量得到的标准值进行对比，结果表明：管路端头的位姿测量误差小于0.05 mm，角度测量误差小于0.1°，而且计算速度快，不引入任何人为操作，有效解决了斜口圆截面管路端头位姿的测量难题。