磁耦合式可调频压电振动俘能器

王淑云， 杜洁雅， 黄喆人， 阚君武， 柴超辉， 张忠华

（浙江师范大学 精密机械与智能结构研究所，浙江 金华 321004）

1 引 言

近年来，随着环境污染的日益严重，社会越来越重视对绿色能源的使用，清洁稳定的能源对人类生活越来越重要，广泛应用于交通运输、军事国防及生产生活等领域［1］。传统化学电池的工作寿命短、质能比过高、更新困难，严重制约了现代微电子器件的进步，因此，基于环境能量回收的微小型发电机的需求不断增加。目前，常见的发电方式有电磁式［2］，静电式［3］及压电式［4-5］。其中，压电式俘能器利用压电效应工作、结构简单、不需要外接电源，更适用于微电子器件和监测系统。

根据使用环境，压电俘能器可分为振动式［6］、旋转式［7］及流体激励式［8］等。压电振动俘能器是通过外界振动激励使压电材料弯曲变形从而实现振动能到电能的转换。然而，自然环境中的振动能具有分布频带较散、频率低、随时间变化的特点［9］，现有的压电振动俘能器大多只能在很窄的频带内工作，俘能器的固有频率无法与外界激励频率相匹配时发电效率较低。针对该问题，人们提出了两种调频方法，一种是通过采用浮动质量［10］、非线性调谐［11］和分段线性调谐［12］等方式进行调频；另一种是通过多模态俘能技术［13］拓宽压电振动俘能器的有效频带，最常见的是利用利用磁力改变俘能器系统刚度来调节谐振频率及拓宽频带。Du 等［14］提出了一种磁力调频压电电磁复合发电机，利用调节磁力间距离调节发电装置的固有频率实现宽频换能。Yang 等［15］通过弹簧连接可移动磁铁，频带相对固定磁铁增加两倍。Wu 等［16］将压电层安装在正弦形状的梁上下表面，能更有效地突破壁垒使峰值电压达1 377 mV。Wang 等［17］提出了一种双磁耦合式压电振动俘能器，通过调节系统参数来改变俘能器的固有频率及拓宽频带。以上压电振动俘能器虽然在增强频率适应性和拓宽频带上有所突破，但压电振子的弯曲方向与环境激励方向一致，难以同时实现可调频、频带拓宽及限幅激励。

本文提出了一种磁耦合式可调频压电振动俘能器，它由分别安装主动磁铁和被动磁铁的激励器和组合换能器构成，通过调节俘能器的结构参数实现低频、宽带、高强度及大振幅振动能量回收。在理论和实验上研究纵摆质量、横摆质量、磁铁间距离及负载电阻对俘能器输出性能的影响，证明磁耦合式可调频压电振动俘能器能够在较宽的频带上实现调频。

2 工作原理

图1 给出了磁耦合式可调频压电振动俘能器的结构原理。该俘能器的主要部件为激励器和组合换能器，激励器由弹簧、纵摆质量块、刚性摆臂及其端部安装的主动磁铁构成，刚性摆臂借助轴承和转轴可实现纵向摆动；组合换能器由横摆质量块、横摆簧片及两侧固定的压电振子和端部安装的被动磁铁构成。主动磁铁和被动磁铁同极相斥，压电振子包括末端弯折的金属基板及其一侧粘接的压电晶片，压电晶片发生单向弯曲故只承受单向压应力，分别用横向距离Lx、纵向距离Ly及竖向距离Lz来表示主被动磁铁间距离L在直角坐标系x，y，z上的投影。

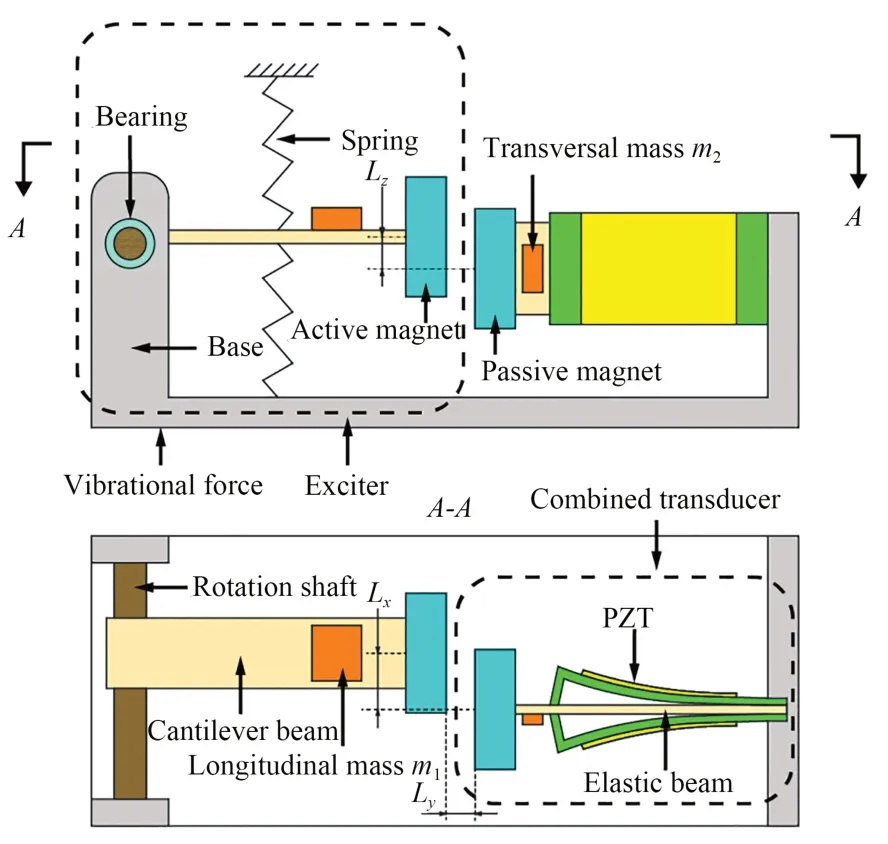
图1 压电振动俘能器结构原理Fig.1 Structure and working principle of piezoelectric vibration energy harvest（PVEH）

工作时，激励器的刚性摆臂在惯性作用下上下摆动，主动磁铁和被动磁铁间位置及磁力发生变化，使横摆簧片往复摆动、压电晶片弯曲，压电振子的形变会随着激励振幅的增大达到最大，然后停止增加，避免外界激励增大时压电振子受到突然冲击而损坏，提高了俘能器的环境适应性。俘能器的输出性能由激励器和组合换能器的结构参数共同决定，故通过调节激励器和组合换能器上质量块质量及磁铁间距离可以提升俘能器的有效带宽和输出电压。

3 仿真分析

3.1 理论建模与仿真分析

根据图1 得到图2 所示的俘能器物理模型。图中，M1，M2分别为激励器和组合换能器的等效质量，C1，C2分别为激励器和组合换能器的等效阻尼，K1，K2分别为激励器和组合换能器的等效刚度，l11，l12及l13分别表示激励器等效质量、激励器等效弹簧及激励器等效阻尼和支点O的距离，P（t）为基础位移，θ（t）为激励器的角位移，x（t）为组合换能器的位移，Fx（t）和Fz（t）分别为磁耦合力的横向分量和竖向分量。

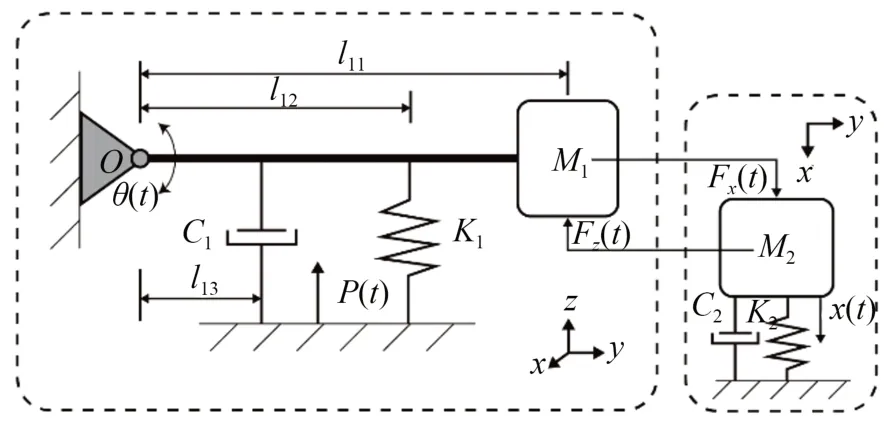
图2 压电振动俘能器的物理模型Fig.2 Energetics model of piezoelectric vibration energy harvest（PVEH）

由振动分析理论建立俘能器系统的振动微分方程为：

根据刚度计算方法得到激励器和组合换能器的等效刚度为：

式中：ks为激励器弹簧刚度，E为横摆簧片的杨氏模量，l2为横摆簧片长度。

根据磁耦合力的计算方法［18］，主动磁铁与被动磁铁间磁力在x与z方向的最大分量为：

式中：μ0为真空磁导率，M为磁力矩。

工作过程中，磁耦合力与磁铁间距离及其重叠面积相关，时域上可以近似视为正弦函数，即：

令P（t）为振动幅值为A的简谐振动，则有：

根据系统振动微分方程进一步计算得到主动磁铁与被动磁铁的位移Z（t）与Y（t），分别为：

式中σ为力的传递系数。

令Ymax为组合换能器的响应幅值，求得组合换能器的位移传递率为：

根据式（9）得到一次压电振子形变产生的电压为［19］：

式中η为与压电材料的结构尺寸和材料特性相关的系数。

由上述公式可知，激励器上纵摆质量m1、组合换能器上横摆质量m2和磁铁受力等因素会影响俘能器的输出性能。这里利用MATLAB 仿真获得m1和m2对俘能器响应特性的影响规律，仿真参数如表1 所示。

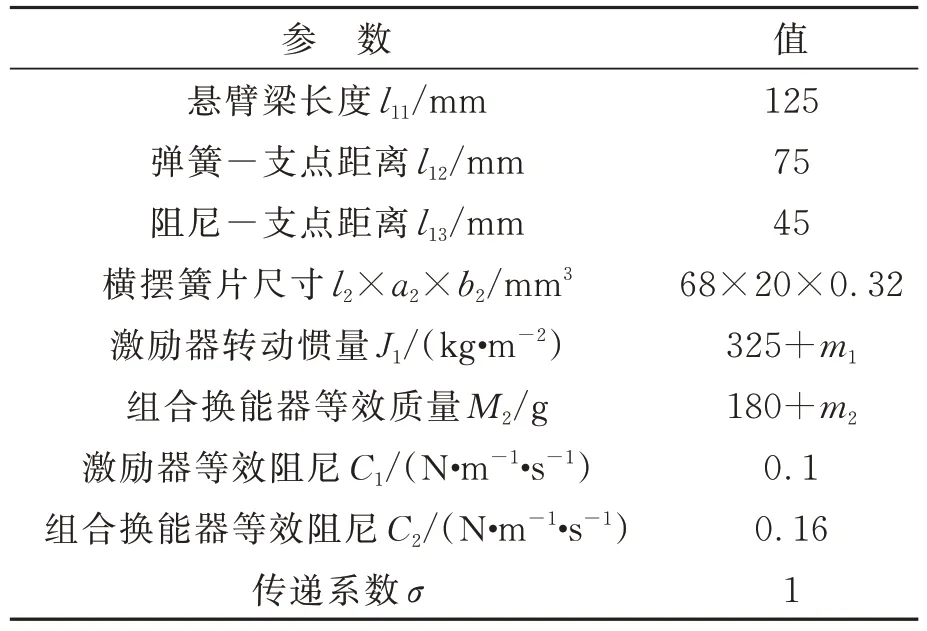
表1 压电振动俘能器的仿真结构参数Tab.1 Simulation structure parameters of piezoelectric vibration energy harvest

图3 为激励器上纵摆质量m1不同时位移传递率β与激励频率的关系曲线。由图可知，存在两阶谐振频率使位移传递率最大，m1主要影响一阶谐振频率及二阶谐振频率对应的位移传递率：m1增大时，一阶谐振频率降低，所对应的位移传递率基本不变；二阶谐振频率基本不变，所对应的位移传递率逐渐减小。由于增大m1相当于增大激励器的等效转动惯量使其谐振频率降低，一阶和二阶谐振频率分别为激励器和组合换能器的谐振频率。

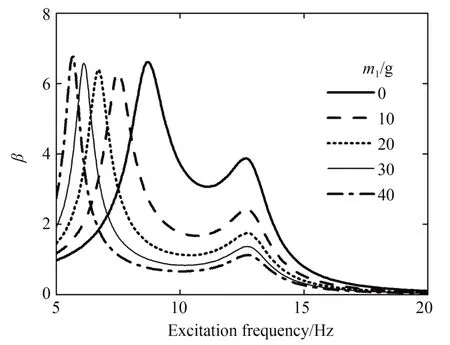
图3 纵摆质量不同时位移传递率与激励频率的关系曲线Fig.3 Relation curves between displacement transmissibility and excitation frequency at different longitudinal mass

图4 为组合换能器上横摆质量m2不同时位移传递率β与激励频率的关系曲线。由图可知，随着m2的增大，一阶谐振频率保持不变，二阶谐振频率减小，所对应的位移传递率均逐渐增大。其原因在于增大m2相当于增大组合换能器的等效转动惯量使其谐振频率降低，两阶谐振频率逐渐靠近，俘能器电压耦合叠加作用加强、输出电压增大。

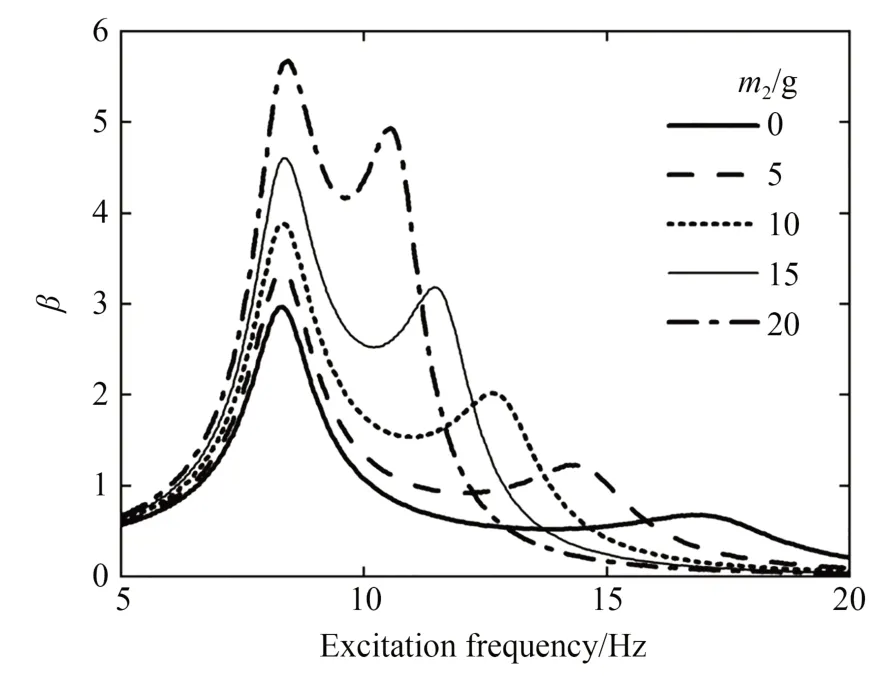
图4 横摆质量不同时位移传递率与激励频率的关系曲线Fig.4 Relation curves between displacement transmissibility and excitation frequency at different transversal mass

综上可知，磁耦合式可调频压电振动俘能器的动力学响应曲线存在两个谐振峰，一阶和二阶谐振频率分别为激励器和组合换能器的谐振频率，改变纵摆质量m1和横摆质量m2可以分别调节俘能器的一阶和二阶谐振频率，两阶谐振频率相差较小时位移传递率较大、相差较大时位移传递率较小，故通过调节m1和m2可以使俘能器在较宽的频带上获得更好的输出性能。

3.2 磁对的有限元建模与仿真分析

根据俘能器的结构原理，组合换能器通过主动磁铁和被动磁铁间的耦合作用获得激振力，激振力与磁铁直径和磁铁间距有关。在实际工作中，主动磁铁和被动磁铁的运动轨迹是非线性的，无法通过计算进行定量分析，故仅研究静态条件下环形磁铁的径向磁力和轴向磁力。基于麦克斯韦方程并利用COMSOL 建立了环形磁对在径向距离lx=0 mm 和轴向距离ly=5 mm 时的磁势云图，如图5 所示。

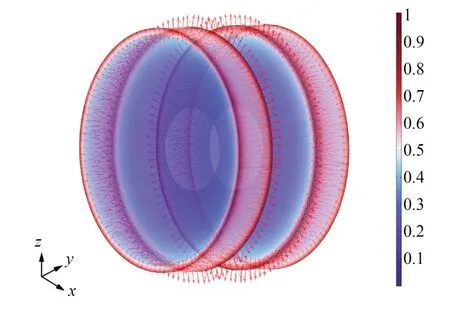
图5 环形磁铁的磁势云图Fig.5 Magnetic potential cloud map of ring magnet

图6 给出了磁铁轴向距离ly=0 mm、直径d不同时径向磁力Fx和径向距离lx的关系曲线。由图可知，在-15 mm＜lx＜15 mm 内，不同直径磁铁的Fx随lx的变化趋势一致，曲线关于lx=0 mm 对称，lx一定时，Fx随着d的增大而增大；在-15 mm＜lx＜0 mm 内，d一定时，Fx随着lx的增大而先增大后减小，在lx=0 mm 时为0 N，并且在lx=-5 mm 时达到最大；在0 mm＜lx＜15 mm内，d一定时，Fx随lx的变化趋势与-15 mm＜lx＜0 mm 时一致，Fx在lx=5 mm 时达到最大。

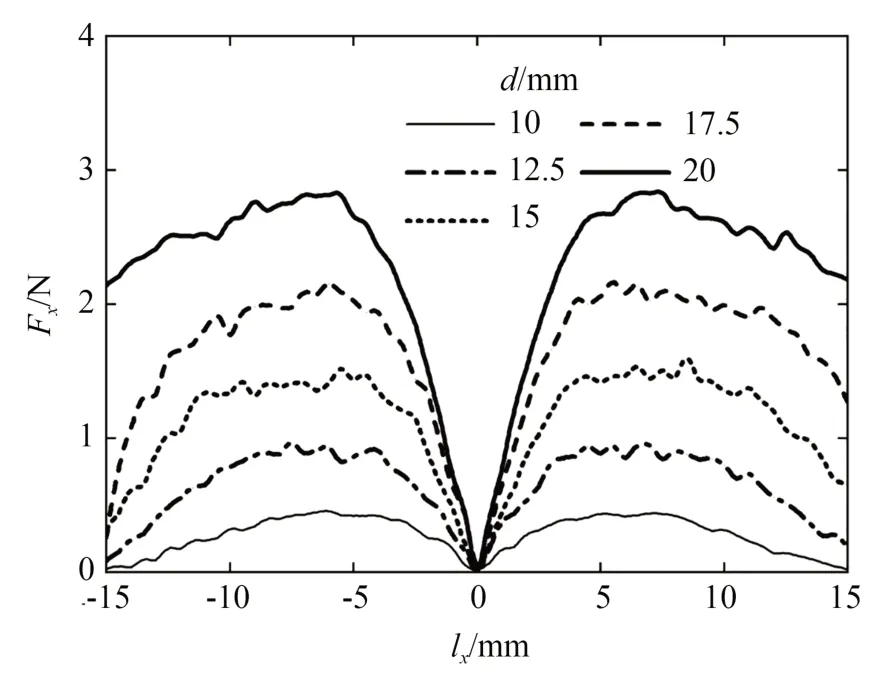
图6 磁铁直径不同时径向磁力和径向距离的关系曲线Fig.6 Relation curves between radial magnetic force and radial distance with different diameters of magnet

图7 给出了磁铁径向距离lx=0 mm、直径d不同时轴向磁力Fy和轴向距离ly的关系曲线。由图可知，在4 mm＜ly＜15 mm 内，轴向距离ly一定时，Fy随着d的增大而增大；磁铁直径d一定时，Fy随着ly的增大呈指数关系减小。

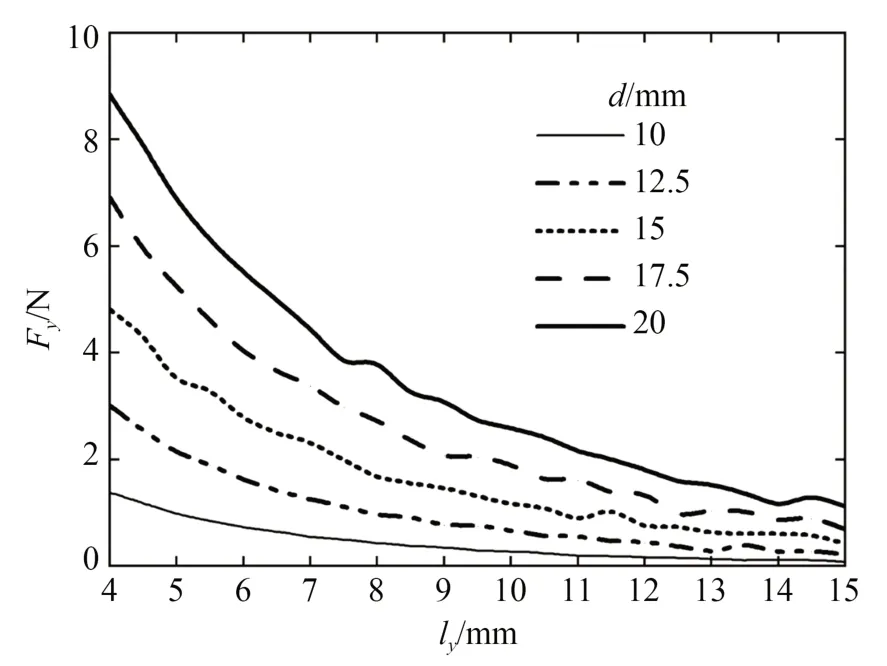
图7 磁铁直径不同时轴向磁力和轴向距离的关系曲线Fig.7 Relation curves between axial magnetic force andaxial distance with different diameters of magnet

由上述仿真结果可知，磁铁直径和磁铁间距都会影响磁力大小，故选择合适的磁铁直径可以获得与环境相适应的磁力，从而提高力的传递效率，改变磁铁间距离可以调节俘能器的输出性能，有效提升俘能器的有效频带和输出电压。

4 实验测试与分析

为验证磁耦合式可调频压电振动俘能器原理的可行性，并获得系统参数对俘能器输出性能的影响规律，设计制作了实验样机并搭建了测试系统，分别如图8 和图9 所示。实验仪器主要包括DC-1000 振动台、SA-15 功率放大器、MSO6014A 型混合信号示波器、RC-2000 信号控制器及电脑控制端变阻箱等，俘能器的相关参数如表2 所示。

表2 压电振动俘能器的结构尺寸参数Tab.2 Structural dimension parameters of PVEH

图8 压电振动俘能器实验样机Fig.8 Experimental prototype of piezoelectric vibration energy harvest

图9 压电振动俘能器测试系统Fig.9 Piezoelectric vibration energy harvest test system

由仿真结果可知，激励器上纵摆质量m1、组合换能器上横摆质量m2及磁铁间距L会影响俘能器的输出性能。为验证理论和仿真的正确性，在其他条件不变的情况下选取合适的磁铁直径，探究m1，m2，Lx，Ly及Lz对俘能器输出电压幅频特性的影响。

图10 给出了纵摆质量m1不同时输出电压与激励频率的关系曲线。由图可知，存在两阶谐振频率使俘能器的输出电压达到峰值，将这两阶谐振频率分别记为f1和f2（f1＜f2），峰值电压分别记为Un1和Un2，图11 为谐振频率f及所对应的输出电压Un与m1的关系曲线。由图10 和图11 可知：m1为0，10，20，30 及40 g 时（f1，Un1）分 别 为（12 Hz，21.6 V），（11.5 Hz，25.6 V），（10.5 Hz，44 V），（10 Hz，30.4 V）及（9.5 Hz，20.8 V）；（f2，Un2）分别为（16 Hz，28.2 V），（16 Hz，24.8 V），（16 Hz，22.4 V），（15.5 Hz，22 V）及（15.5 Hz，19.2 V）。由此可知，m1增大时，f1减小，f2基本不变，Un2减小，Un1先增大后减小并在m1=20 g 时达到最大，实验结果与图3 数值仿真结果基本一致。

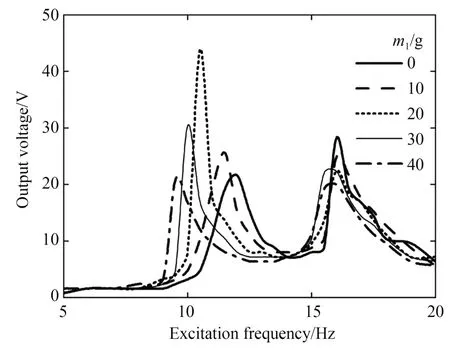
图10 纵摆质量不同时输出电压与激励频率的关系曲线Fig.10 Relation curves between output voltage and excitation frequency with different longitudinal mass

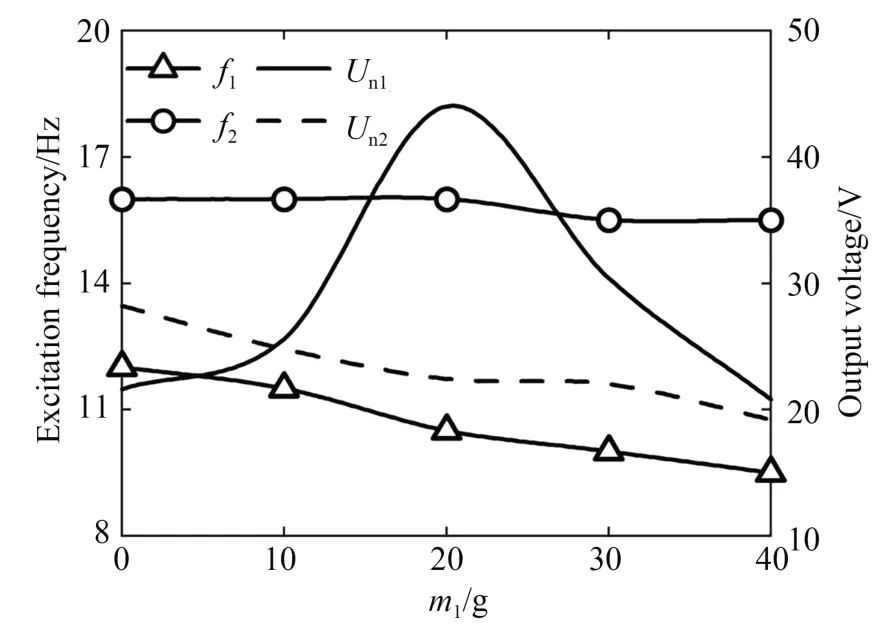
图11 谐振频率及输出电压与纵摆质量的关系曲线Fig.11 Relation curves between output power and excitation frequency with different longitudinal mass

图12 给出了横摆质量m2不同时输出电压与激励频率的关系曲线，图13 为谐振频率f及它对应的输出电压Un与m2的关系曲线。由图12 和图13 可知：当m2为0，5，10，15 及20 g 时，（f1，Un1）分别为（11 Hz，20.8 V），（11 Hz，21.2 V），（11.5 Hz，24 V），（11 Hz，27.2 V）及（10.5 Hz，28 V）；（f2，Un2）分 别 为（18 Hz，22.4 V），（16 Hz，24.8 V），（14.5 Hz，25.6 V），（13.5 Hz，28.8 V）及（13 Hz，34.4 V）。由此可知，m2增大时，f1基本不变，f2减小，Un1和Un2增大，该结果与图4 数值仿真结果基本一致。

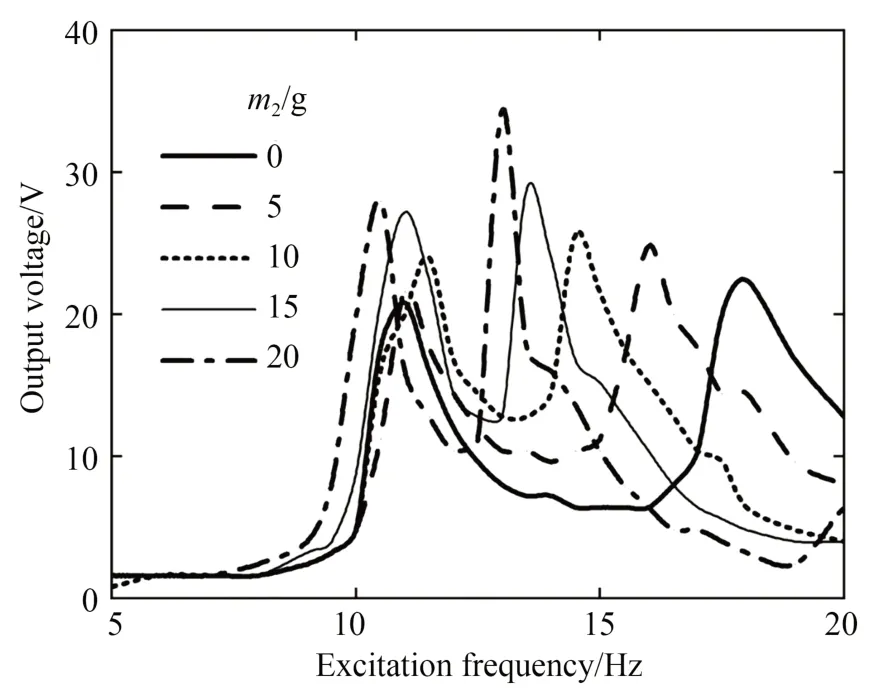
图12 横摆质量不同时输出电压与激励频率的关系曲线Fig.12 Relation curves between output voltage and excitation frequency with different transversal mass

图14 给出了横向磁铁间距Lx不同时输出电压与激励频率的关系曲线，图15 为谐振频率f及它对应的输出电压Un与Lx的关系曲线。由图14和图15 可知：当Lx为0，5，10，15 及20 mm 时，（f1，Un1）分别为（12.5 Hz，26.4 V），（11.5 Hz，29.6 V），（11.5 Hz，24 V），（11 Hz，22.4 V）及（11 Hz，15.2 V）；（f2，Un2）分别为（12.5 Hz，26.4 V），（14 Hz，22.4 V），（15.5 Hz，26.4 V），（16 Hz，29.6 V）及（16 Hz，30.4 V），即Lx增大时，f1逐渐减小，f2逐 渐 增 大，Un1先 增 大 后 减 小，Un2先 减 小 后 增大，在Lx=0 mm 时f1和f2重合，输出电压Un1达到最大值。结合图6 的仿真结果可知，随着Lx的增大，磁铁间径向磁力先增大后减小，这与实验中Un1先增大后减小的结果一致；此外，Lx增大时，f1和f2的差值逐渐增大，说明频带逐渐变宽，故调节Lx可以满足拓宽频带、提高俘能器的环境适应性的实际需求。

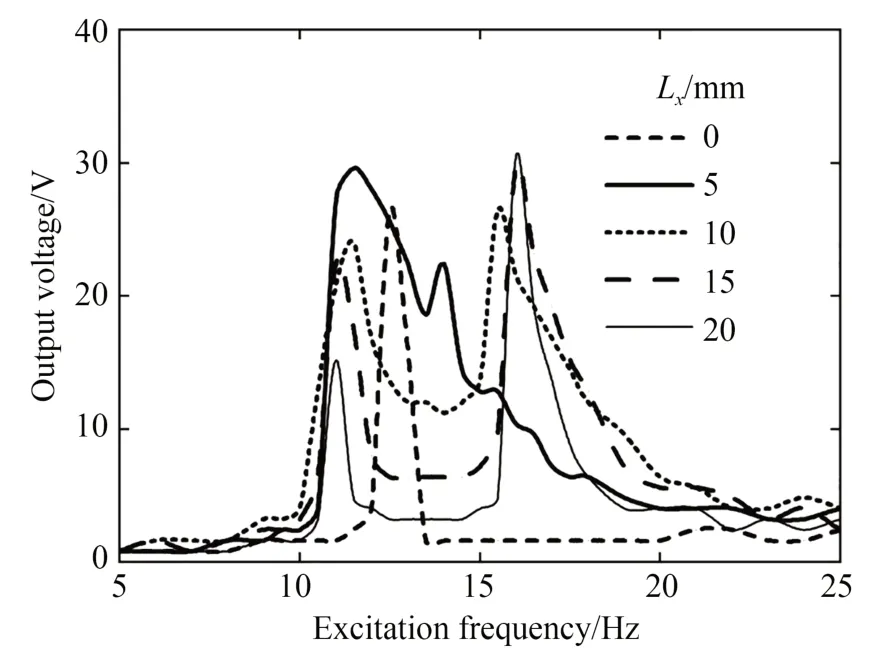
图14 横向磁铁间距不同时输出电压与激励频率的关系曲线Fig.14 Relation curves between output voltage and excitation frequency with different transversal magnet spacings

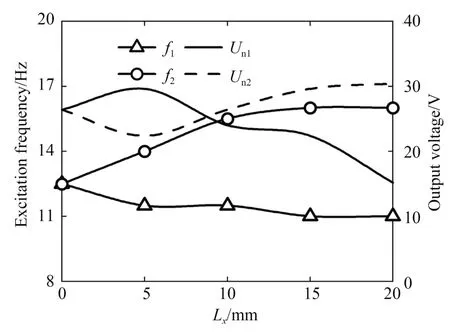
图15 谐振频率及输出电压与横向磁铁间距的关系曲线Fig.15 Relation curves between output power and excitation frequency with different transversal magnet spacings

图16 给出了纵向磁铁间距Ly不同时输出电压与激励频率的关系曲线，图17 为谐振频率f及它对应的输出电压Un与Ly的关系曲线。由图16和图17 可知：当Ly为5，7.5，10 及15 mm 时，（f1，Un1）分别为（11.5 Hz，34.4 V），（11 Hz，14.4 V），（11.5 Hz，11.2 V）及（11 Hz，4.8 V）；（f2，Un2）分别为（15.5 Hz，23.2 V），（15 Hz，27.2 V），（14.5 Hz，24 V）及（14.5 Hz，17.6 V），即Ly增大时，f1基本不变，f2小幅减小，Un1和Un2均逐渐减小。结合图7 的仿真结果可知，Ly的增大使磁铁间的轴向磁力减小，压电振子变形量减小导致输出电压Un1和Un2减小；此外，当Ly减小时f1和f2的差值增大，即有效频带逐渐变宽，且输出电压Un1和Un2增大，故存在合适的Ly使俘能器获得较高的输出电压和较宽的有效频带。

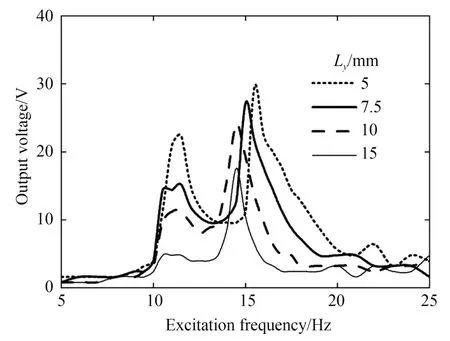
图16 纵向磁铁间距不同时输出电压与激励频率的关系曲线Fig.16 Relation curves between output voltage and excitation frequency with different longitudinal magnet spacings

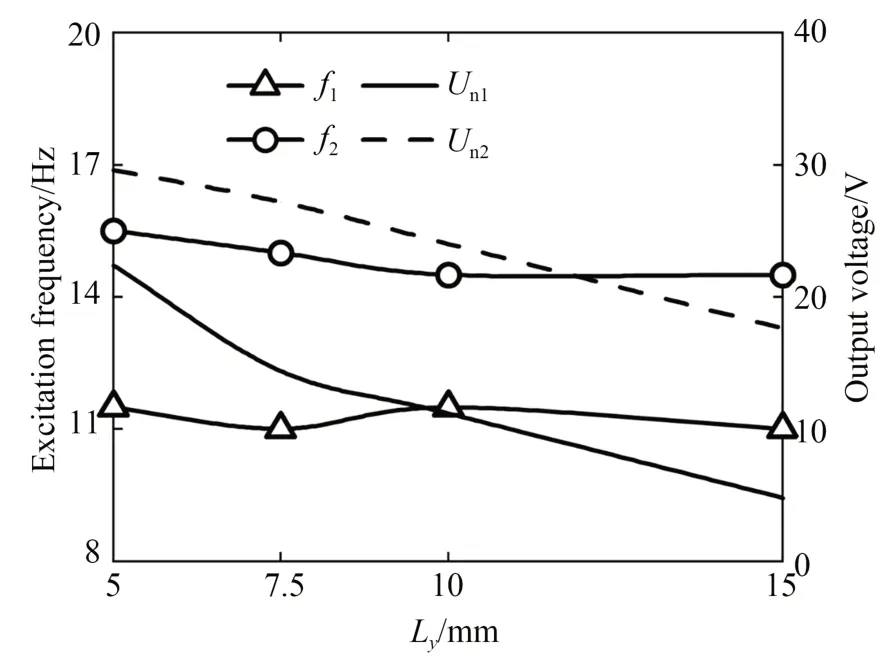
图17 谐振频率及输出电压与纵向磁铁间距的关系曲线Fig.17 Relation curves between output power and excitation frequency with different longitudinal magnet spacings

图18 给出了竖向磁铁间距Lz不同时输出电压与激励频率的关系曲线，图19 为谐振频率f及它对应的输出电压Un与Lz的关系曲线。由图18和图19 可知：当Lz为0，5，10，15 及20 mm 时，（f1，Un1）分别为（9 Hz，12.8 V），（9.5 Hz，10.4 V），（10 Hz，16 V），（11.5 Hz，33.6 V）及（11.5 Hz，16 V）；（f2，Un2）分别为（20 Hz，14.4 V），（20 Hz，14.4 V），（17.5 Hz，20.8 V），（15 Hz，29.6 V）及（15.5 Hz，12 V），即随着Lz的增大，在0 mm＜lz＜15 mm 内，f1增大，f2减小，Un1和Un2整体趋势均由缓变快大幅增大；在15 mm＜lz＜20 mm 内f1和f2基 本 不 变，Un1和Un2逐 渐 减 小，在lz=15 mm 时Un1和Un2达到最大值。俘能器的输出电压变化主要由两方面决定，一方面是横摆簧片受到磁力使压电振子弯曲产生电能，故在不考虑其他影响条件的情况下输出电压随磁力的增大而增大；另一方面是横摆簧片在摆动时会受到主动磁铁的阻力作用，阻力变大会引起横摆簧片的弯曲量变小、输出电压变小。Lz较小时横摆簧片受到的磁力虽大，但摆动时阻力也很大，此时Un1和Un2较小；Lz继续增大到15 mm 时，横摆簧片摆动受到的阻力较小，故Un1和Un2大幅增大；Lz增大到15 mm 之后由于距离过大，组合换能器受到的磁力较小，故Un1和Un2逐渐减小。

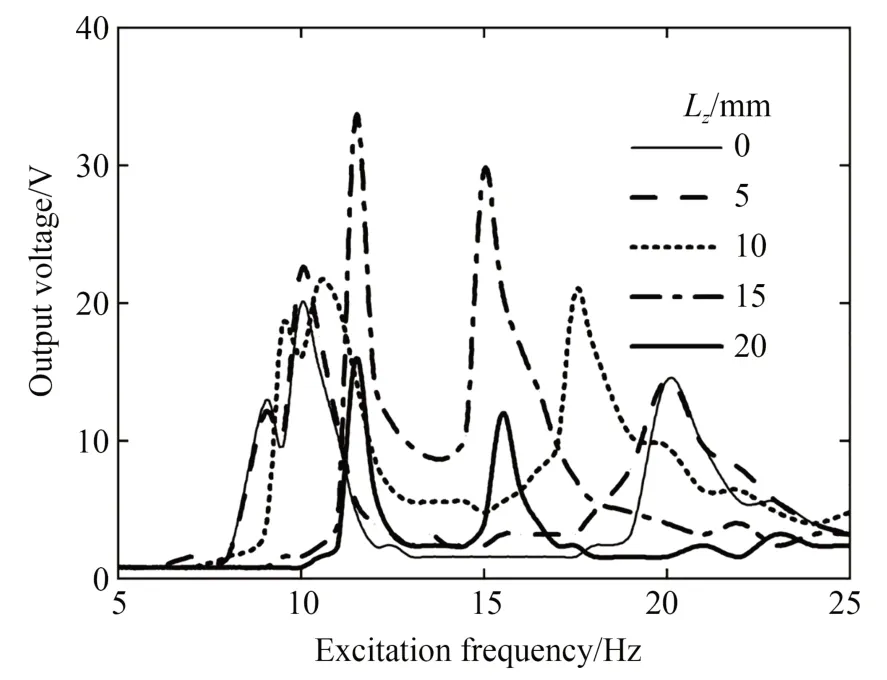
图18 竖向磁铁间距不同时输出电压与激励频率的关系曲线Fig.18 Relation curves between output voltage and excitation frequency with different vertical magnet spacings

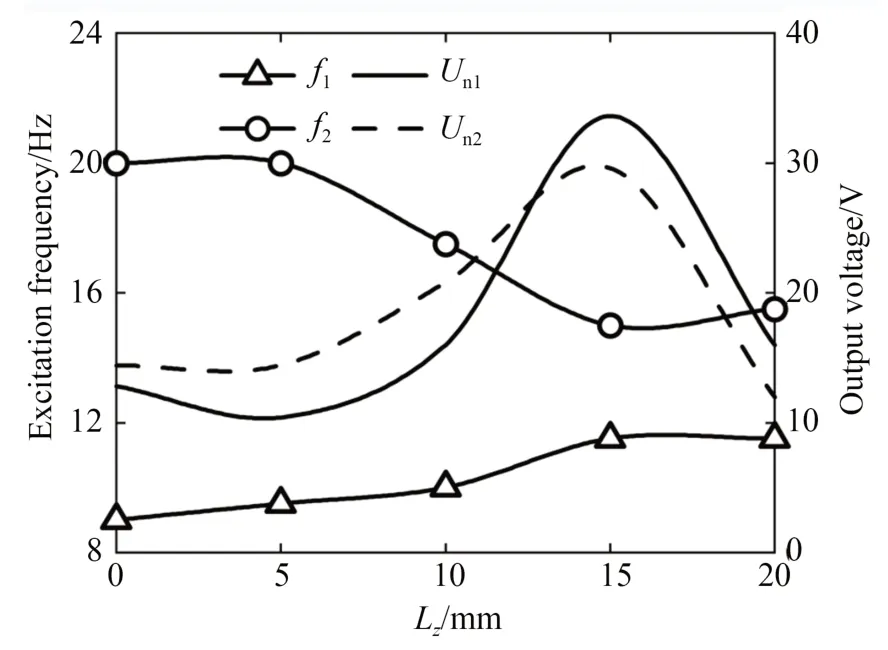
图19 谐振频率及输出电压与竖向磁铁间距的关系曲线Fig.19 Relation curves between output power and excitation frequency with different vertical magnet spacings

图20 给出了不同激励频率下输出功率与负载电阻R的关系曲线。功率测试中，俘能器的结构参数选取与表2 相同。将俘能器外接两个整流桥，再以串联的方式连接到负载电阻上进行输出功率测试。由图可知，负载电阻和激励频率都会影响俘能器的输出功率，各激励频率下都存在最佳负载电阻使俘能器的输出功率最大；当激励频率为15 Hz，负载电阻为2 200 kΩ 时，俘能器的最大输出功率为0.122 mW。

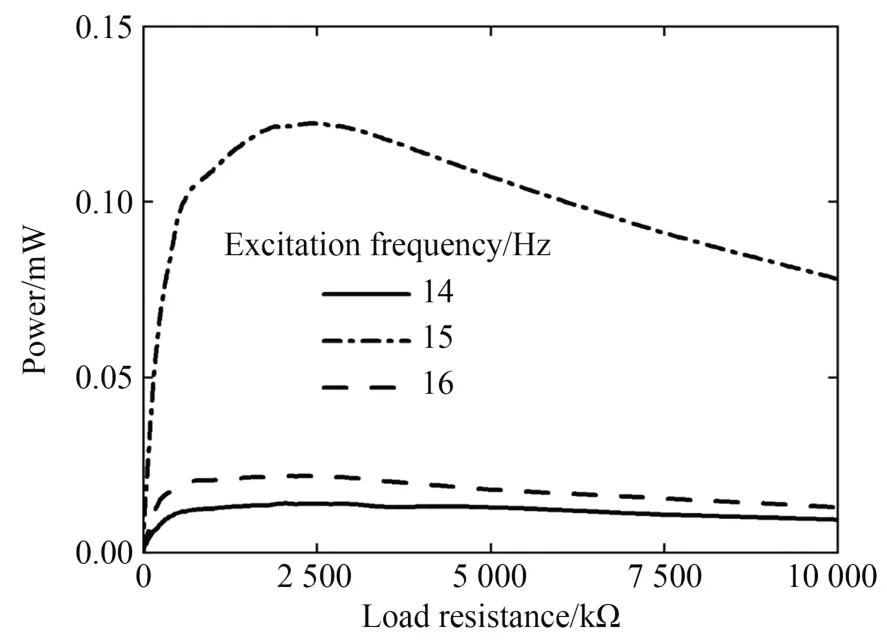
图20 激励频率不同时输出功率与负载电阻的关系曲线Fig.20 Relation curves between output power and load resistance at different excitation frequencies

表3 给出了不同压电振动俘能器之间的性能对比。相比之下，本文提出的磁耦合式可调频压电振动俘能器在环境适应性和输出性能方面均有提升，能够更好地满足微电子器件和监测系统自供电的需求。

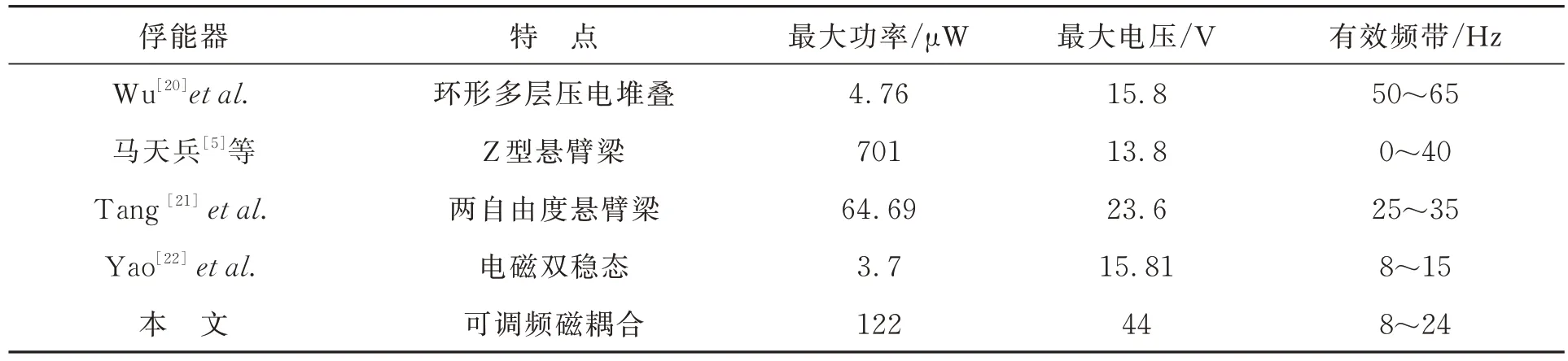
表3 压电振动俘能器的性能比较Tab.3 Performance comparison of PVEHs

5 结 论

本文建立了磁耦合式可调频压电振动俘能器的物理模型，获得了俘能器纵摆质量及横摆质量与组合换能器位移传递率的关系，通过有限元建模仿真获得了磁铁直径及磁铁间距与磁力的关系，在此基础上选取较佳的磁铁直径制作了实验样机并进行实验，得到了纵摆质量、横摆质量和磁铁间距离对俘能器输出性能的影响规律。在激励频率小于20 Hz 时，俘能器存在两阶谐振频率f1和f2，使它达到峰值电压Un1和Un2，f1和f2分别为激励器和组合换能器的谐振频率。当纵摆质量m1增加时，f1减小，f2保持 不变；当横 摆质量m2增加时，f1保持不变，f2减小，f1和f2互相靠近时其对应的电压Un1和Un2会显著增大，故可通过调节俘能器的纵摆质量和横摆质量来改变有效带宽和输出电压，以适应低频、宽频带的自然振动环境。Lx增大时，f1减小，f2增大，Un1先增大后减小，Un2先减小后增大；Ly增大时，f1不变，f2小幅减小，Un1和Un2均 逐 渐 减 小；随 着Lz的 增 大，在0 mm＜lz＜15 mm 内，f1逐 渐 增 大，f2减小，Un1和Un2均由缓变快大幅增大，在15 mm＜lz＜20 mm内，f1和f2基本不变，Un1和Un2逐渐减小，故可通过改变磁铁间距来调节两阶谐振频率及其对应的输出电压。存在最佳负载电阻使输出功率最大，当激励频率为15 Hz，负载电阻为2 200 kΩ 时，俘能器的最大输出功率为0.122 mW。