适应大范围星场密度变化的恒星辨识与抑制

杨禹凯， 谷 健， 王建立， 刘俊池

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049；3.吉林省智能波前传感与控制重点实验室，吉林 长春 130033；4.中国人民解放军63768部队，陕西 西安 710200）

1 引 言

随着航天科技的发展，越来越多的航天器被送入太空，逐渐拥挤的太空环境对航天器在轨运行安全构成很大威胁。为避免航天器、空间碎片［1］等发生碰撞，同时掌握重点航天器的在轨运行状态，利用地基光学望远镜［2］对目标进行观测并生成高精度的定位与测光信息，是有效的空间监视［3-4］手段之一。

中高轨目标的搜索效率［5-6］与视场大小正相关，因此中高轨望远镜的光学视场普遍较大。大视场望远镜在搜索中高轨目标时，图像中除中高轨目标外还存在恒星目标。恒星与中高轨目标在图像中呈点状或线状［7］，除此之外再无附加的轮廓特征，因此普遍基于速度差异对目标与恒星进行辨识［8］。在某种程度上，恒星速度辨识就等同于恒星辨识。中高轨目标最有效的搜索方法是凝视搜索，在指定的搜索天区，望远镜保持固定的方位与俯仰指向，图像中的大量恒星呈现同向匀速直线运动，而目标则相对静止或缓慢运动，因此计算恒星速度［9］，并对具有此速度的目标进行抑制，是中高轨目标成功检测的必要环节之一。

银河是位于银河系平面上的一条明亮的带状结构，由数十亿颗恒星及星际物质组成，在观测银道面附近天区时，图像中的恒星密集程度非常高［10］。当存在云雾遮挡等恶劣条件时，视场中可探测的恒星数量非常少［11］。由此可见，在中高轨目标搜索过程中，恒星场密度的变化区间非常大，这给恒星或恒星速度辨识带来了很大的难度，直观表现为恒星或恒星速度辨识失败，进而导致恒星虚警情况的发生。因此，研究适应大范围星场密度变化的恒星辨识与抑制方法，对提升中高轨目标检测具有重要意义。

当前，恒星抑制方法主要有图像差分法［12］、Top-hat 变换法［13］和全局航迹关联法［14］。其中，图像差分法容易出现恒星边缘残像；Top-hat 变换法需依据恒星及中高轨目标在图像中的空间分布选取合适的结构算子，工程实现较难；全局航迹关联法相对成熟，具有较高的稳定性。然而，前述恒星抑制方法均依赖于恒星速度的准确辨识。现有的恒星速度辨识方法主要有灰度投影法［15］、傅里叶梅林法［16］、速度众数法［17］，以及基于天文定位的惯性坐标关联法［18］。这些恒星速度辨识方法均要求视场中存在适量的恒星，恒星数量过少，则计算存在失效风险；恒星数量过多，灰度投影法会计算失效；当视场内存在突出的云雾、杂光特征时，傅里叶-梅林法会计算失效。

针对当前方法的局限性，本文在惯性坐标关联法的基础上，拟基于地平坐标系与惯性坐标系的数学转换关系计算恒星在图像中的惯性坐标，并由此实现恒星辨识。该方法可行性的前提是：在存在静态系统误差的条件下，恒星惯性坐标计算值与真值存在较大差异，但相邻图像帧的恒星惯性坐标计算值的时域相对差异较小，满足恒星辨识需求。该方法不依赖天文定位过程，解决了稀疏星场下天文定位失效引起的恒星辨识失败问题，并大幅缩短了运算时间。

2 现有方法局限性分析

2.1 恒星抑制方法

2.1.1 图像差分法

基于已知的恒星速度对图像序列进行配准，然后采用图像差分法对恒星进行抑制。图1（a）、1（b）为凝视模式下拍摄的两帧连续图像，图像差分法得到的恒星抑制效果如图1（c）所示。从图中不难发现，图像差分法处理后，恒星边缘仍存在残像，这些残像会干扰目标航迹关联。

图1 图像差分恒星抑制Fig.1 Stellar suppression with image differencing method

2.1.2 Top-hat 变换法

基于形态学的Top-hat 变换法广泛应用于图像背景抑制领域。依据恒星速度及曝光时间选取合适的结构元素对原始图像做灰度开运算，得到仅包含恒星的背景图像，并利用图像差分处理原图和背景，实现恒星抑制。Top-hat 处理过程如下：

式中：f为输入图像，belement为结构元素，fTop-hat为恒星抑制处理后的图像。Top-hat 变换的恒星抑制效果受限于选取的结构元素。凝视模式下，恒星速度在图像域中直观表现为匀速直线，恒星星象呈拉线状，如图2 所示。

图2 结构元素选取需参考的空间分布Fig.2 Spatial distribution in consideration for selecting structuring element

2.1.3 全局航迹关联

基于已知的恒星速度对图像中恒星及中高轨目标构成的数据集合进行多帧匹配，判断每一个观测目标点的航迹属性，将航迹满足恒星速度约束的目标点视为恒星进行抑制。算法流程如图3 所示。

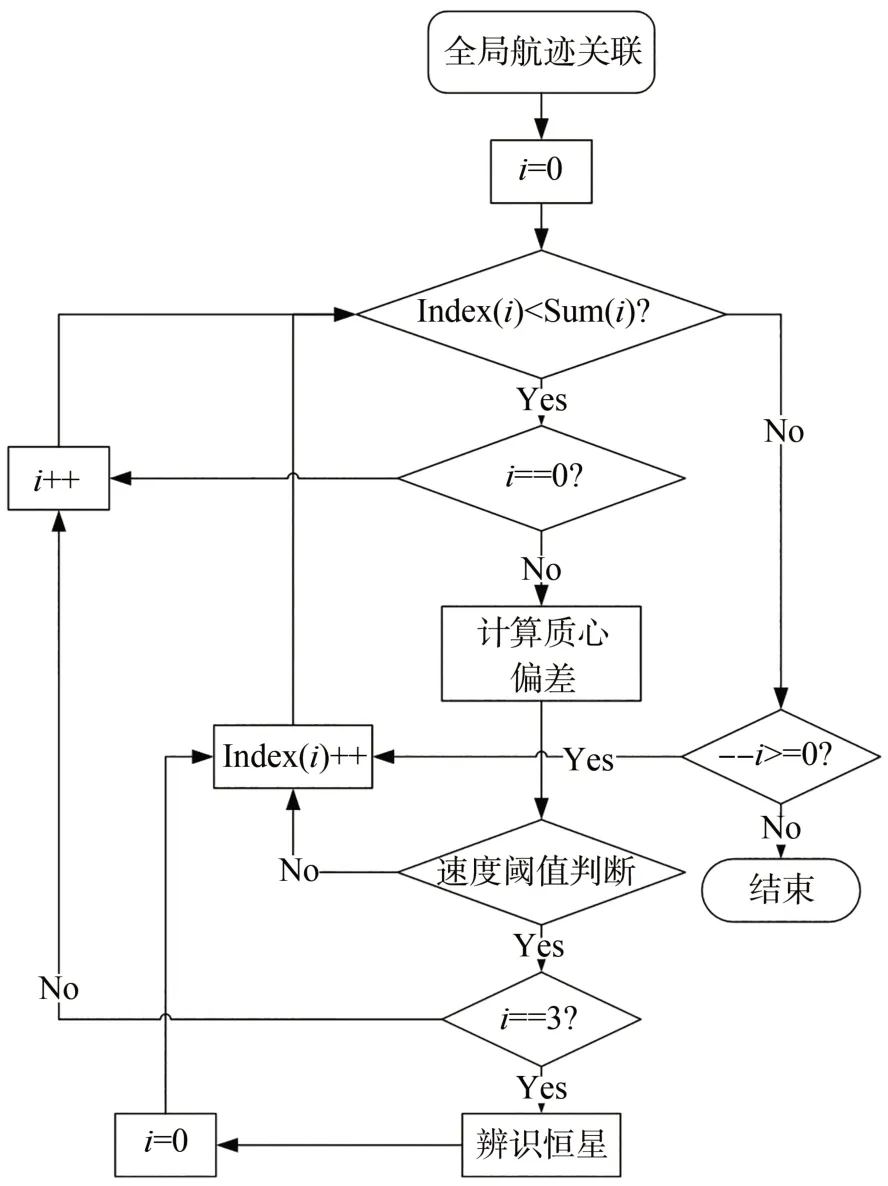
图3 全局航迹关联算法流程Fig.3 Flow chart of global track association algorithm

2.1.4 局限性分析

（1）图像差分法：由图1（c）可知，因地基光学望远镜存在抖动等外部因素的影响，恒星在相邻两帧间的光度信息并不一致，灰度分布存在差异。帧差处理结果会出现恒星边缘残像，中高轨目标搜索可能出现虚警。

（2）Top-hat 变换法：结构算子需小于图像中最小恒星且大于最大中高轨目标的尺寸需求。选取过小会导致中高轨目标被抑制，过大则导致恒星残留。

（3）全局航迹关联：该方法是基于点集的数据处理，不依赖图像中的灰度分布及空间信息，相对成熟，具有较高的稳定性。在图像坐标系下，受像旋影响，视场边缘与视场中心的恒星速度存在偏差，在进行航迹关联时可能导致恒星残留，为抑制视场边缘的恒星需进一步放大阈值，但存在目标被视为恒星而抑制的风险。

2.2 恒星速度辨识方法

2.2.1 灰度投影法

利用相邻帧的灰度投影曲线进行互相关计算得到恒星速度，过程如下：

其中：M表示图像总行数，rProj（i）表示第i行的行灰度投影。基于行灰度投影计算互相关函数：

其中：rProjcur与rProjref表示相邻两帧图像的行灰度投影，m是固定值，表示最大间隔行数，两帧间隔行数随w的变化而变化。存在wmin使Rheight（w）最小，此时rProjcur与rProjref的灰度投影相似度最高，两帧间隔行数（wmin-m-1）即为图像垂直方向上的偏移量vy；同理，可求得图像在水平方向上的偏移量vx。（vx，vy）即为恒星速度。

2.2.2 傅里叶-梅林

通过计算图像序列在频域的相位差，表征相邻两帧图像的相对位置关系，由相位相关技术求得帧间的偏移量从而获得恒星速度，算法过程如下：

其中：f1（x，y），f2（x，y）为相邻两帧图像在空域上的灰度分布，（dx，dy）为图像在水平与垂直方向上的偏移量，F1（u，v），F2（u，v）分别表示f1，f2对应的傅里叶变换，仅存在相位上的不同。计算两帧图像的互能量谱：

其中F2（*u，v）为F（2u，v）的复共轭。平移理论表明，互能量谱的相位等于图像间的相位差，对它进行傅里叶反变换，得到冲击函数δ（x-dx，ydy）。此函数在平移位置处有明显的尖锐峰值，其余位置处的值趋近于零，峰值处对应的偏移量即为恒星速度。

2.2.3 速度众数法

对相邻两帧图像中恒星与中高轨目标所构成的数据集合进行关联计算，得到速度分布直方图，其中频率最高的对应值即为恒星速度，算法流程如下：

算法 1.速度众数法输入： 相邻帧中的目标数据集合：Point1，Point2第m 帧中第n 个目标的质心在图像中的像素坐标：posxmn，posymn速度集合vecSpd输出： 速度众数：vx，vy 1： initialize： i=0，j=0 2： for i = 0 ： Point1.size（）-1 do 3： for j = 0 ： Point2.size（）-1 do 4： 计算两帧中任意两目标的质心在水平与垂直方向上的偏差：dx2j_1i=abs（posx2j-posx1i）dy2j_1i=abs（posy2j-posy1i）将（dx2j_1i，dy2j_1i）加入vecSpd 5： end for 6： end for 7： vx，vy为vecSpd 出现次数最多的对应值

2.2.4 基于天文定位的惯性坐标关联法

惯性坐标系是一种相对固定的坐标系，其基准面是天赤道，具有相对于地球的位置和方向相对固定的特殊性质，在地球上以惯性坐标系来描述恒星的位置时，可以忽略短时间内恒星的位置变化。

在惯性坐标系下定位图像中的恒星多采用星表匹配方法，利用天文定位技术，将观测视场内的恒星与预先建立的恒星数据库进行匹配。基于匹配结果。计算得出该帧图像所对应的实际天球区域位置信息，并由此反算得到恒星速度。

2.2.5 局限性分析

前述恒星速度计算方法在图4 所示星场密度变化或云雾遮挡的场景下存在相应的局限性。

图4 星场密度稀疏、密集及云雾遮挡场景下的实测图像Fig.4 Measured images for sparse stellar density， dense stellar density， and cloud cover scenes

（1）灰度投影法：在星场密度变化的场景中，互相关函数难以反映图像在水平和垂直方向上的全局变化，计算会失效。

（2）傅里叶-梅林法：时间复杂度相对较高，难以满足对中高轨目标搜索的实时性需求。另外，在云层遮挡等因素而导致图像中恒星数量较少的情况下，相邻帧之间的整体运动特性不再以恒星为主导，计算会失效。

（3）速度众数法：在视场中恒星数量较少的情况下，恒星的运动特性难以形成显著的统计特征，计算会失效。此外，在星场密度较高的情景下，该方法耗时较长。

（4）基于天文定位的惯性坐标关联法：高精度天文定位依赖于观测视场内充足的参考恒星。在视场中恒星较少的情况下，匹配精度难以满足要求，存在计算失效的风险。

3 算法原理

本文基于天文学原理，推导地平坐标系和惯性坐标系之间的数学转换关系，计算恒星在图像中的惯性坐标并通过相邻两帧图像的关联匹配实现恒星辨识与抑制。相较于传统的天文定位方法，该方法具有更好的稳定性和高效性，能够解决稀疏星场下天文定位失效引起的恒星辨识失败问题，同时能大幅缩减计算时间，满足实时性需求。

3.1 计算目标在惯性坐标系下的赤经赤纬

3.1.1球极坐标系转换原理

天文学中通常使用球极坐标系来定义坐标，如图5 所示。其中，r为点P和原点的 距离，θ为r和z轴的夹角，φ为r在xy平面上的投影逆时针方向与x轴的夹角。r为1 时，笛卡尔坐标系与球极坐标系之间的转换如下：

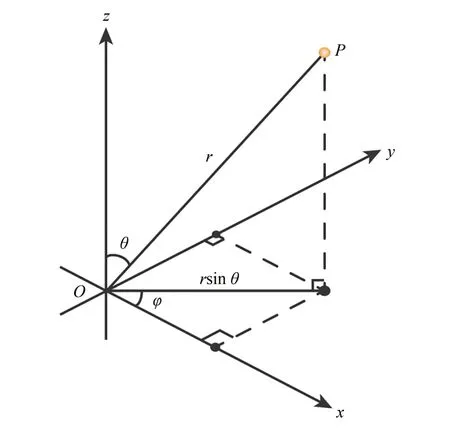
图5 球极坐标系Fig.5 Spherical coordinate system

其中：xyz坐 标 系 沿y轴 旋 转 角 度χ得 到 的x'y'z'，如图6 所示。

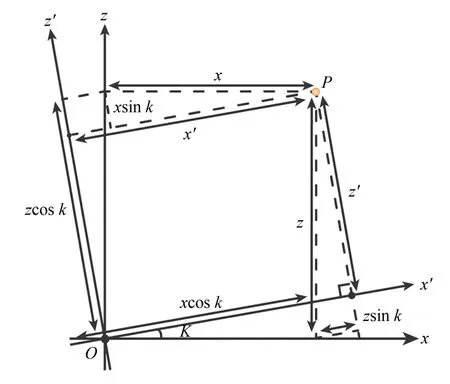
图6 两球极坐标系转换Fig.6 Transformation of two spherical coordinates

对应关系如下：

将式（6）代入式（7）得到两球极坐标系转换方程：

依据这一变换原理，引入时角坐标系作为中介，实现从地平坐标系到惯性坐标系的连续坐标转换。

3.1.2地平坐标系转时角坐标系

光线在穿过地球大气时发生折射，目标在观测时的位置会产生偏差。基于测站气压、温度等环境信息，计算大气折射修正值并应用到方位角上，使观测数据更加准确，计算过程如下：

其中：RASt表示每角秒对应的弧度值，P和T分别表示测站气压和温度。

时角表示观测目标所在子午圈与观测站点所在子午圈之间的角度差，受地球自转影响，恒星的时角随时间匀速增长。如图7 所示，目标在地平坐标系下的方位角Az、俯仰角h，在时角坐标系下的时角H、赤纬δ以及站址纬度φ与式（8）中的角度有如下关系：

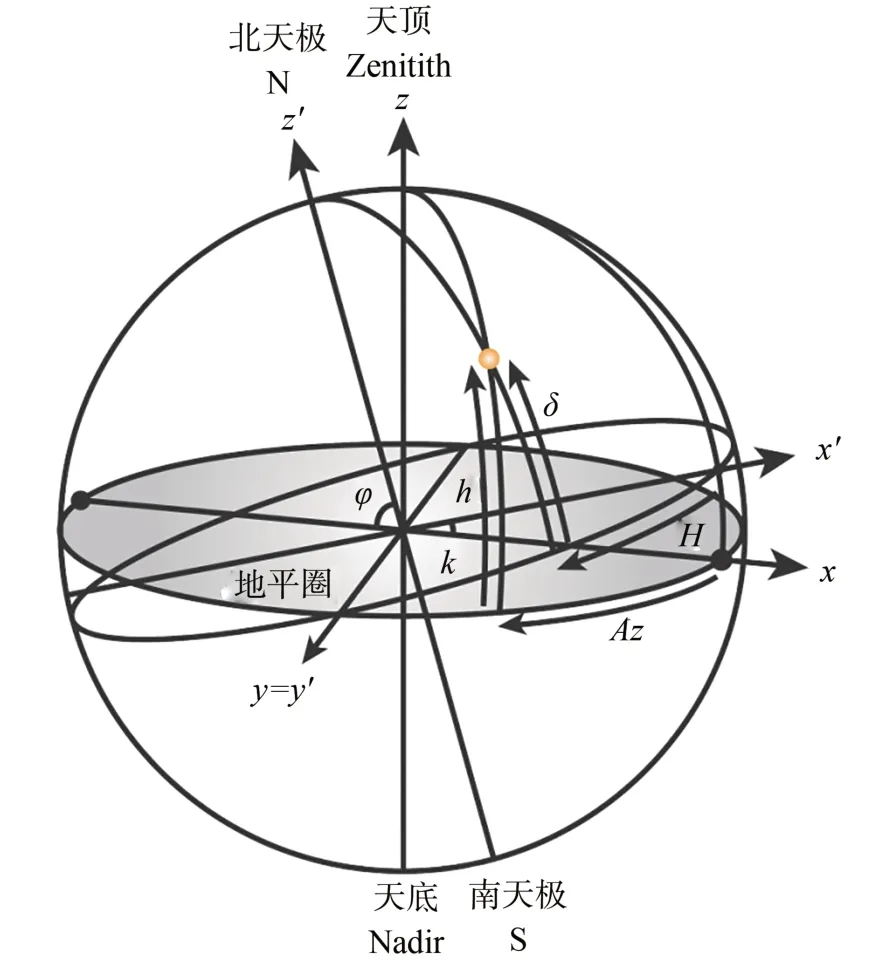
图7 时角坐标系Fig.7 First equatorial system （HA-dec）

将式（10）代入式（8）后化简即可求得目标在时角坐标系下的时角H与赤纬δ：

3.1.3时角坐标系转惯性坐标系

惯性坐标系中，目标的赤纬值δ与时角坐标系下一致。在惯性坐标系（J2000.0）中，赤经定义为从春分点起始，沿逆时针方向至观测目标所在子午圈的夹角，如图8 所示。依据曝光中心时刻的北京时与站址经度，计算春分点的时角即地方恒星时Hγ：

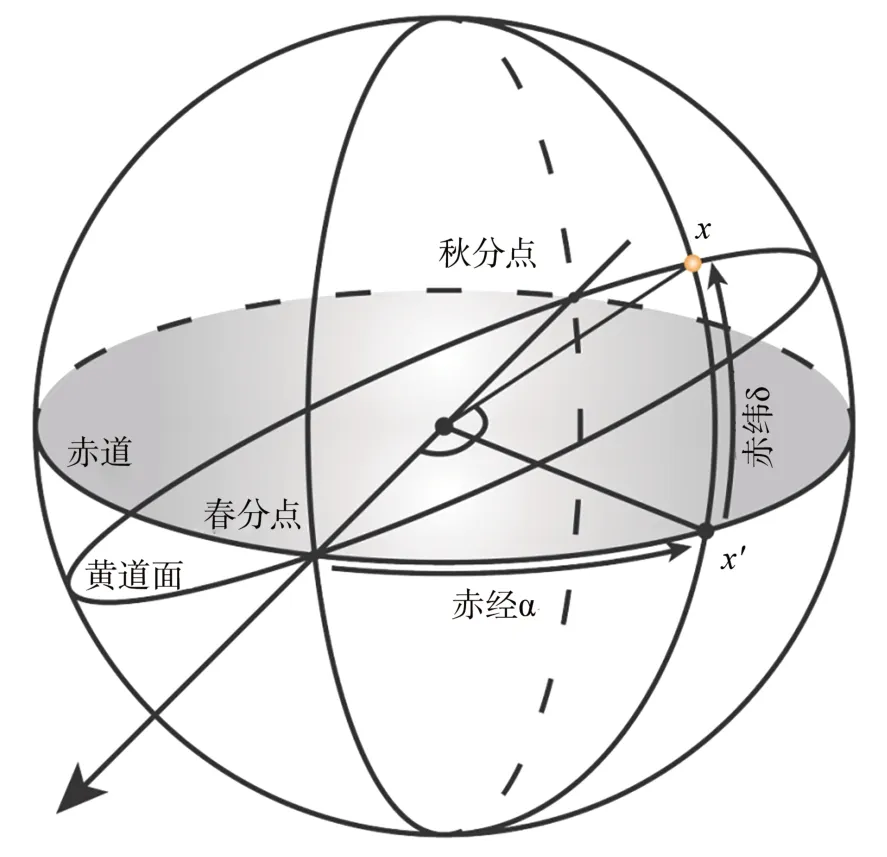
图8 惯性坐标系Fig.8 Second equatorial system （RA-dec）

其中：S为格林尼治恒星时，longiutude为测站经度。S的计算过程如下：

其 中：S0为d日世界 时的恒星 时，1+μ为平太 阳日和恒星日的比例关系。S0的计算过程如下：

其中Tu的计算过程如下：

其中jd为所求日期当天时的儒略日数，2 451 545.0为UTC2000 年1 月1 日12 时的儒略日数。由式（12）～式（15）即可求得地方恒星时Hγ。依据惯性坐标系下赤经的定义，赤经α为地方恒星时Hγ与时角H之差，目标在惯性坐标系下的赤经α与赤纬δ表示为：

3.2 相邻帧关联匹配辨识与抑制恒星

为实时检测与跟踪中高轨目标，地基光学望远镜的图像采集系统帧频较高，连续两帧图像的时间间隔内，恒星在惯性坐标系中的位置信息相对不变。依据3.1 理论推导，计算图像中恒星及中高轨目标在惯性坐标系下的赤经赤纬位置信息，对构成的数据集合进行相邻帧关联匹配，算法流程如下：

算法 2.惯性坐标关联匹配法输入： 相邻帧中的恒星及中高轨目标数据集合：Point1，Point2第m 帧中第n 个目标点的质心在惯性坐标系下的赤经赤纬：αmn，δmn阈值：dThreshold速度波门：fRadius输出： 提取出的恒星集合：StarBlob 1： initialize： i=0，j=0 2： for i = 0 ： Point1.size（） - 1 do 3： for j = 0 ： Point2.size（） - 1 do 4： 计算两帧中任意两目标的质心在水平与垂直方向上的偏差：dx2j_1i=abs（posx2j-posx1i）；dy2j_1i=abs（posy2jposy1i）5： 计算两帧中任意两目标在惯性坐标系下的赤经赤纬差值：dα2j_1i=abs（α2j-α1i）；dδ2j_1i=abs（δ2j-δy1i）6： if 像素偏移值小于fRadius，且赤经赤纬小于dThreshold 7： 将第1 帧中的第i 个目标与第2 帧中的第j 个目标视为同一恒星加入StarBlob 8： end if 9： end for 10： end for

天球经线在高赤纬区域具有较高密度，随着惯性坐标系中赤纬值的增加，视场中每单位像素所对应的赤经差值逐渐扩大。因此，dThreshold的设定需结合目标在天球中的纬度信息，即：

其中dThreshInit表示阈值初始值。该算法能辨识出每颗恒星在相邻帧中对应的目标点，将辨识得到的恒星数据集合StarBlob从原有集合中剔除实现恒星抑制。

4 惯性坐标系时域相对不变性验证

静态系统误差是由地基望远镜在观测过程中的指向偏差引起的，导致图像中的恒星和中高轨目标在地平坐标系下的方位角和俯仰角与真实值存在偏差。因此，根据3.1 计算得出的结果会有不可忽视的绝对误差。然而，相邻图像帧的恒星惯性坐标计算值的时域相对差异较小，满足恒星辨识需求，具有时域相对不变性。

设测站地理位置为经度125°23'13.2''、纬度43°51'0.72''，曝光中心时刻为北京时间2023 年3月16 日13 时39 分0 秒，环境信息为温度10 ℃、气压102 kPa。依据3.1 计算流程，确定地平坐标系中天球地平以上不同方位角Az和俯仰角h位置处的恒星在惯性坐标系下的赤经α与赤纬δ。

对固定的方位角Az及俯仰角h，分别在静态系统误差为2″，5″，10″的条件下，保持时空和测站环境信息不变。根据相同的计算过程，得到此时对应方位角Az'、俯仰角h'位置处的恒星在惯性坐标系下的赤经α'及赤纬δ'，与理论真值α，δ之差即为绝对误差。结果如图9 和表1 所示。

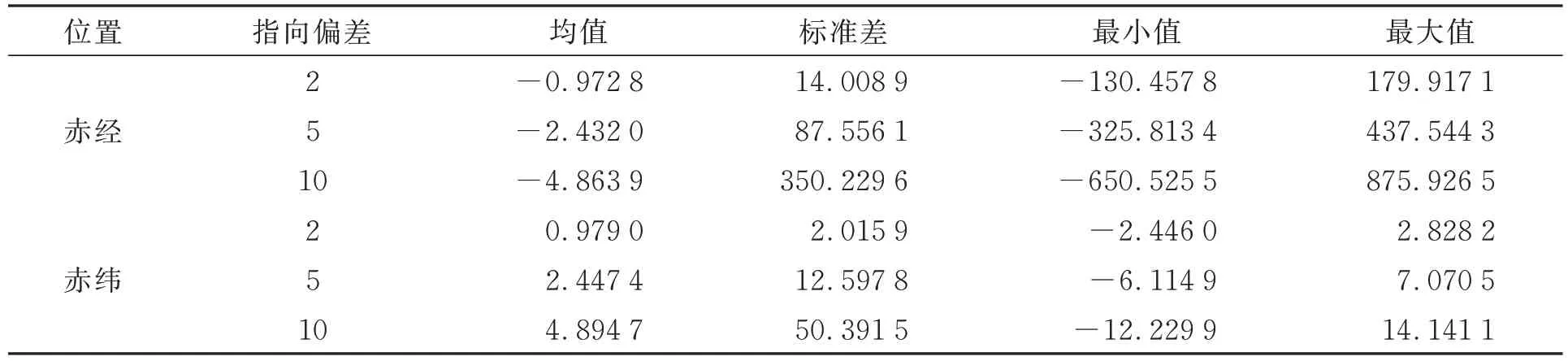
表1 静态系统误差为2″，5″，10″条件下的赤经及赤纬的绝对误差Tab.1 Absolute errors of right ascension and declination under condition of static system error of 2″，5″ and 10″ (″)

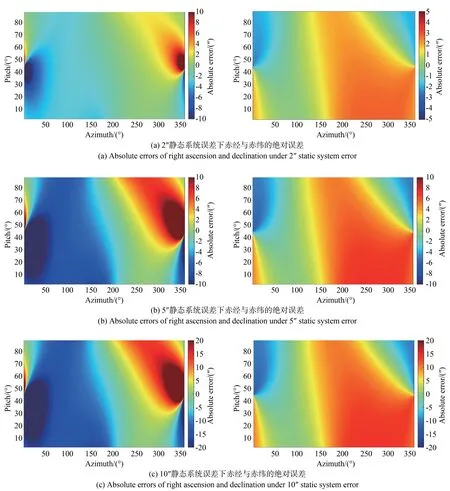
图9 静态系统误差为2″，5″，10″条件下的赤经及赤纬的绝对误差Fig.9 Absolute errors of right ascension and declination under condition of static system errors of 2″，5″ and 10″， respectively

相邻两帧图像的时间间隔为10 s 时，计算下一曝光中心时刻地平坐标系下相同位置处的恒星在惯性坐标系下的赤经α″及赤纬δ″，与α'及δ'之差即为相对差异，结果如图10 和表2 所示。

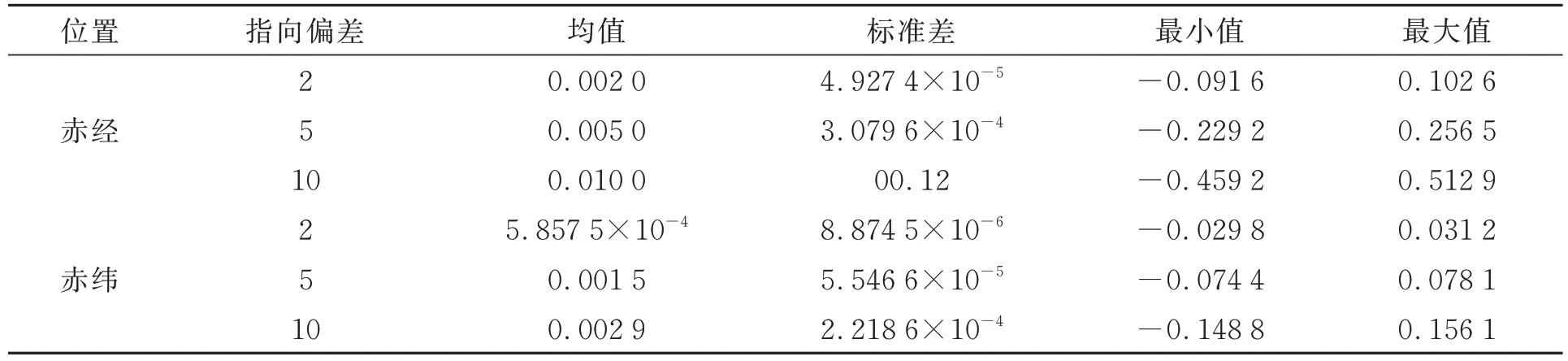
表2 10 s 时间间隔条件下赤经及赤纬的相对差异Tab.2 Relative differences of right ascension and declination under time interval of 10 seconds （″）

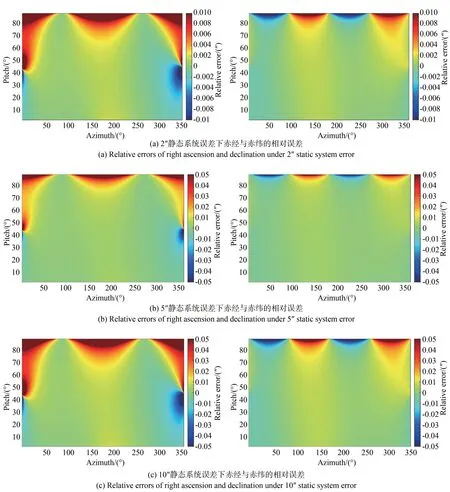
图10 不同静态系统误差在时间间隔为10 s 条件下的赤经及赤纬的相对差异Fig.10 Relative differences of right ascension and declination under different static system errors with time interval of 10 s

分析结果显示，恒星在惯性坐标系下的赤经、赤纬绝对误差与静态系统误差呈正相关。尽管绝对误差的平均值稳定在个位量级，其标准差却相对较大。在各个方位角和俯仰角的组合条件下，绝对误差的波动范围较广，最大误差值甚至高达数百角秒。因此，静态系统误差对计算结果的影响显著，不可忽视。而恒星在惯性坐标系下赤经、赤纬的相对差异均值稳定在10-3″数量级，标准差稳定在10-5″数量级，最大值仅为0.5″，连续两帧图像中，同一恒星在惯性坐标系下的位置信息相对差异很小。这一结果验证了惯性坐标系具有良好的时域相对不变性，满足恒星辨识需求，同时证明了本研究所提恒星辨识与抑制方法的可行性。

5 实验与结果分析

5.1 实验平台

实验平台硬件配置为Intel Xeon E5-2699 v4 处 理 器、RTX2080Ti 显 卡 及Teledyne Dalsa公司生产的Xtium-CL MX4 图像采集卡。在Linux Ubuntu 16.04 操作系统上基于Qt 5.12.9开发框架自研了上位机应用程序，为提高算法的运行效率，利用OpenCL 与OpenMP 并行计算框架实现GPU 与CPU 双端加速，用户界面（UI）设计简洁易用，数据处理显示面板如图11所示。

图11 数据处理软件显示面板Fig.11 Display panel of data processing software

5.2 仿真分析

针对不同星场密度下的连续图像序列，分别采用灰度投影法、傅里叶-梅林法、速度众数法、基于天文定位的惯性坐标关联法及本文所提方法对恒星进行辨识，处理结果如表3 所示。

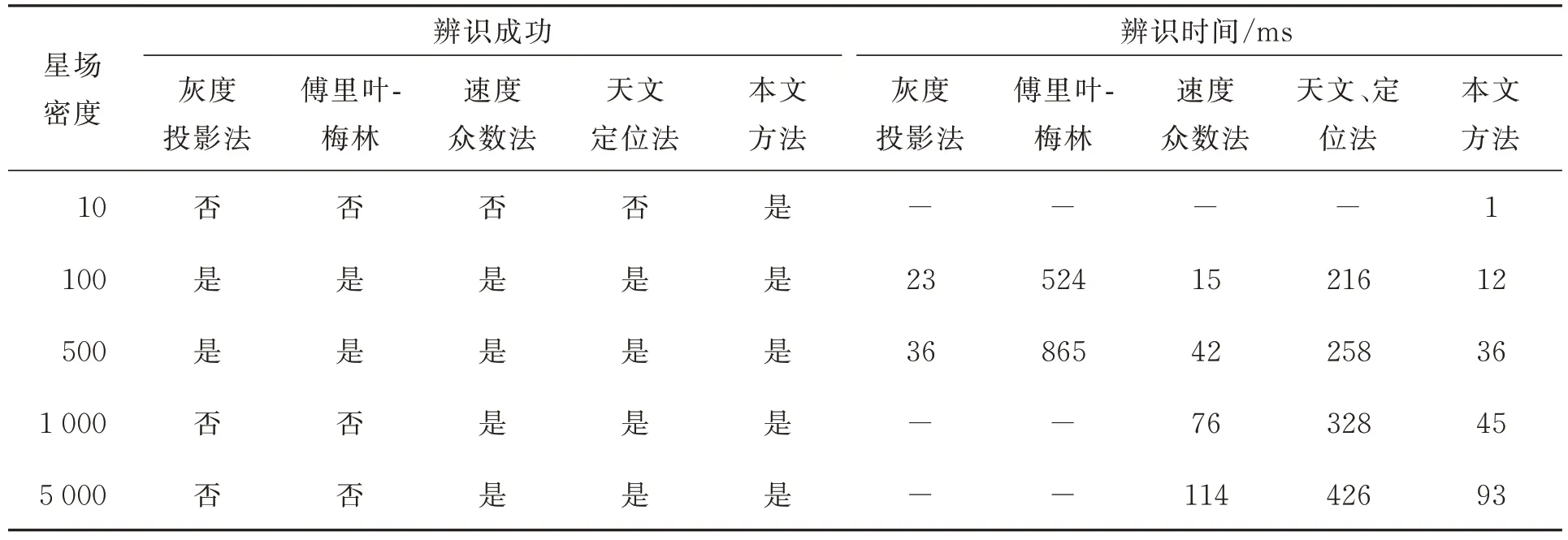
表3 各恒星辨识方法在不同星场密度下的处理结果Tab.3 Processing results of different stellar identification methods under different star field densities

由仿真分析结果可知，在星场密度稀疏场景下，仅本文所提方法能有效辨识恒星。在密集星场下，灰度投影法与傅里叶-梅林法失效，基于天文定位的惯性坐标关联法的辨识时间相对较长，而本文所提方法不仅能成功辨识恒星，而且耗时相对较短，实时性能更优。

5.3 外场验证

本研究依托某大视场望远镜，视场为2.5°×2.5°，面阵为6 144×6 144，极限探测能力为17星等。观测夜气象环境良好，在凝视搜索模式下对指定天区进行观测，实验数据采用拍摄所得的连续图像序列。

为验证本文所提恒星辨识与抑制方法能适应大范围星场密度变化，对星场密度适中、密集、或遭遇云雾遮挡而恒星数量较少3 种情景下的实测图像各进行100 圈次验证。结果如图12 所示，均未发生恒星虚警及中高轨目标检测缺失的现象，证明本方法具有良好的准确性与稳定性。

图12 星场密度适中、密集、云雾遮挡恒星稀疏3 种情景下的实测图像及本文方法验证结果Fig.12 Measured images and validation results of proposed method under moderate star field density， dense star field density， and sparse star field density due to cloud or fog obstruction

6 结 论

本文提出的基于惯性坐标时域相对不变性的恒星辨识与抑制方法简洁高效，易于工程实现，在确保实时性的前提下具有较强的外场适应能力。首先，基于理论推导的地平坐标系与惯性坐标间的数学转换关系计算恒星在图像中的惯性坐标，该方法根本性地解决了在星场密度稀疏、密集或遭遇云雾遮挡等情况下恒星速度辨识失效，导致恒星抑制效果不理想的问题。实验结果表明，与传统方法相比，该方法在恒星辨识与抑制上具有更高的稳定性和准确性。