线性空间上线性变换可逆的若干等价条件
周慧倩
(洛阳师范学院 数学科学学院,河南 洛阳 471934)
0 引言
线性空间是高等代数的重要研究对象,是研究客观世界中线性问题的重要理论.线性变换则是线性空间上最基本的一种变换,它反映了线性空间中元素之间的线性联系.几何上的旋转变换、镜面反射、相似变换、切变等都是线性变换[1].线性变换在泛函分析、积分方程等数学分支中都起着十分重要的作用.力学上描述物体的形变也涉及线性变换,计算机图形学中也经常用到线性变换.研究线性变换对数学以及力学、物理、计算机、工程等众多学科都有重要的意义[2].
线性变换可以定义乘法、加法、数乘以及逆运算,数域P上n维线性空间V上的全体线性变换关于加法和数乘构成线性空间L(V).通过线性变换与它在给定基下矩阵的对应,L(V)与P上全体n×n矩阵构成的线性空间Pn×n可建立同构关系[3]193.线性空间L(V)对于乘法也是封闭的,但是逆运算却不是普遍可以进行的,只有部分线性变换是可逆的.文献[4][5]列举了线性变换可逆的一些充分必要条件.本文在此基础上更深入而全面地探讨这一问题,并且在一些证明中采用了不同的方法和思路.首先介绍可逆线性变换的定义和几点性质,然后结合矩阵理论和映射理论,从线性变换的矩阵、特征值、值域、核以及同构等多个角度进行分析,得到线性变换可逆的若干个等价命题.考虑到无限维情形的特殊性,本文仅在有限维线性空间上讨论.
1 可逆线性变换的定义及性质


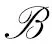

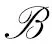

那么
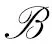
说明逆变换唯一.
由于L(V)中可逆线性变换的和不一定可逆,因此V的全体可逆线性变换不构成L(V)的子空间.


性质3说明V的全体可逆线性变换的集合对于乘法满足封闭性,性质2说明该集合中任一元素有逆元,考虑到映射有结合律,V的恒等变换显然是可逆线性变换,可作为单位元,因此我们有以下结论.
性质4V的全体可逆线性变换关于映射乘法构成群,称为可逆线性变换群或非退化线性变换群.
2 线性变换可逆的若干等价条件






证明先证明(1)⟺(2).
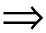


AD=E,
说明矩阵A可逆.
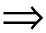

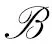
于是
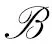
因此
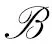
再证明(1)⟺(3).



即
k1ε1+k2ε2+…+knεn=0.



接下来证明(2)⟺(4).

|A|=λ1λ2…λn,
A可逆的充分必要条件是|A|≠0,即λ1λ2…λn≠0,也即λi均不为0.
最后证明(1)⟺(5).
f(x)=|xE-A|=xn-(a11+…+ann)xn-1+…+(-1)n|A|.

f(x)=anxn+an-1xn-1+…+a1x+a0(a0≠0)


两边同时除以常数项得
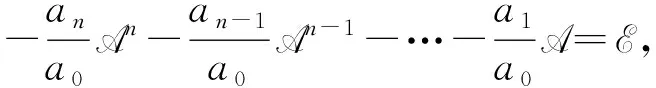
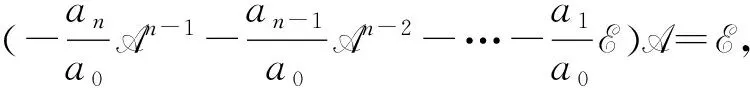
联系线性变换的值域与核以及映射理论,还可以得到线性变换可逆的几个等价条件.














证明接着证明(1)⟺(6).




再由引理3,可得(6)⟺(7)⟺(8).
接下来证明(1)⟺(13).








3 结语
定理1、2给出了有限维线性空间上线性变换的14个等价命题,分别从矩阵、基、特征值、值域和核以及映射等角度进行研究,得到了线性变换可逆的13个充分必要条件.结合高等代数中的其他知识,我们还可以继续研究这一问题,派生出更多的等价命题.另外,如果考虑无限维线性空间的情形,会有什么样的结论,也是非常值得探讨的问题.

