基于剪切变换及凸集映射的2D数据重建技术研究

钱 峰

(黄山学院 网络与信息管理中心,安徽 黄山 245041)

0 引言

高分辨率图像检测在数字应用中变得越来越重要.例如,医学图像MRI和CT需要能够显示出人眼无法辨别的细微病灶,而卫星图像则至少需要能够识别出人的长相和汽车的车牌号码.在集成电路生产中,检测装置都需要足够高分辨率的图像来保证测量和控制的精度[1].然而,受困于成像感光元件CMOS和CCD的噪声污染,实际应用中,图像信噪比往往不够高,图像分辨率不但不会增加反而会降低[2].因此,图像数据重建技术为信噪比差的图像提供了良好的解决方案.

目前,图像数据的重建研究主要可以分为两大类: 空间域和频域(变换域)的处理[3].空间域的图像数据重建理论方法有迭代反向投影法、非均匀样板内插法、最小二乘法、自适应滤波法、估计法和凸集映射等.这些处理方式基本上是傅立叶分析方法的延续[4].基于频域的处理方法包括逆滤波算法、维纳滤波法、去卷积R-L法、基于小波域边缘保存正则化法和高斯去模糊法[5].

近年来,比较流行高维度稀疏数据法,其通过再降维收敛方式提高稀疏程度[6].主要的方法包括人工神经网络、支持向量机和深度学习等[7-8].本研究将采用剪切变换理论来探讨图像数据的重建工作.通过剪切变换(Shearlet Transform)的数据稀疏表达能力,对图像数据进行升维分解,然后对获得的数据通过降维投影到原空间,之后在原空间内找到缺失数据的投影,并结合集合论中的凸集映射理论,来进行图像数据的重建工作.

1 相关理论概述

1.1 离散剪切变换的实现方法

1.1.1 剪切变换的频域离散实现过程

(1)

通过上述分析,Shearlet变换在某一固定尺度上的频域实现步骤为[10]: 在时间域,实现图像的多分辨率分解,形成子带编码,具体可使用拉普拉斯金字塔变换或高斯矩阵将图像faj - 1[n1,n2]分解成高频子带fdj[n1,n2]和低频子带faj[n1,n2],高频子带描述的是图像信息的细节特征,低频子带描述是图像的轮廓特征,之后分别对两个子带进行傅立叶变换,仍然在伪极网格坐标系中计算,得到矩阵Pfdj; 然后对矩阵Pfdj利用带通滤波器进行滤波处理; 之后重新定义笛卡儿采样坐标后,并对每个子带进行二维快速傅立叶反变换; 最后对滤波后数据的伪极反方向进行快速傅立叶变换,并相加得到剪切系数.

1.1.2 剪切变换的时域实现

为了提升剪切变换频域实现的算法效率,同时,为了减少大尺寸算子的应用产生的吉布斯效应[11],本研究采用时间域的剪切变换.离散傅立叶域的剪切变换系数可根据式(2)计算:

(2)

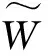
(3)

1.2 凸集映射(POCS)方法的基本原理

凸集映射(Projection on Convex Sets,POCS)或交替投影法是一种在两个封闭凸集的交集上找到一个点的方法.投影过程是指从给定向量空间的任意一点开始,一直投影到找到满足所有凸约束集的解为止.重建过程可以定义为:

(4)

其中,yk(x,y)为第k帧低分辨像,hk(x,y,i,j)为点扩散函数,k=1,2,…,N,N为低分辨图像的帧数,μ(x,y)为噪声.如果凸集投影算子定义为P={p1,p2,p3,…,pn},其中n为集合P的个数.则凸约束集可定义为:

Ck(i,j)={f(i,j):|rk(x,y)|≤δk},

(5)

(6)

其中,δ=cσ,σ为标准噪声差.重建图像在凸集Ck(i,j)上的投影为:

(7)

1.3 结合POCS的剪切变换数据重建

众所周知,如果两个不在同一直线上的向量可以组成一个二维空间,那么这两个向量称为基向量,假设: 图像缺失的数据是Y,原始图像元素为X1,X2,它们构成一个二维空间或平面(X1,X2,Y).当向量Y与二维图像空间垂直时,向量Y在X1和X2该空间上的投影为零(见图1a); 当向量Y与二维图像空间平行时,向量Y在该空间上的投影就是它本身(见图1b); 当向量Y与二维空间不平行也不垂直时,向量Y在二维空间上存在投影(见图1c),此时对应的方程组无解,但存在最优解.在基向量上分布乘某一系数,不能得到全部向量Y,但可以得到部分的投影向量P.为了使向量Y最大,问题就变成了如何使投影向量P最大,这个投影向量P可以分解成投影向量P和误差向量e的组合,当误差向量e在垂直一维空间中最小时,投影P最大.

图1 Y和二维空间的关系

1.4 图像质量的衡量指标

1.4.1 信噪比

信噪比(Signal to Noise Ratio,SNR)用来比较期望信号的强度与背景噪声.它被定义为信号功率和噪声功率之间的比值,用分贝(dB)表示.比值大于1(高于0分贝)表示信号大于噪声.通常,信噪比用于描述电子信号,但也可以应用于各种其他形式的信号.信噪比的定义是:

(8)

式中Gt为最大灰度值,Gb为像素灰度平均值,σ为像素灰度的标准差.

1.4.2 峰值信噪比

峰值信噪比(Peak Signal to Noise Ratio,PSNR)是指信号能够表征的最大功率与影响其表征精度的破坏性噪声功率之间的比值.由于许多信号具有非常宽的动态范围,因此PSNR通常用对数分贝(dB)为单位表示.峰值信噪比的定义是:

(9)

式中MAXI为图像点颜色的最大数值,如果每个采样点用8位表示,那么最大值就是 255.MSE为图像像素点均方差.

2 结果分析

2.1 实验环境

测试环境: 操作系统为Windows 10,处理器为Intel(R) Core(TM) i5-6500,内存为6GB DDR4 RAM,仿真平台为Python 3.7和Matlab 2010a,数据处理采用Origin 8,图像重建采用Shearlab 3D,标准库文件采用Open CV.本研究以Barbara图像为研究对象,Barbara原图像如图2所示,图像格式为JPG的灰度图,尺寸为512×512.

图2 Barbara原图像

2.2 傅立叶变换及频域滤波

为了检验离散剪切变换在图像数据重建中的效果,分别测试数据缺失比例为40%、50%和70%的图像重建效果,不同缺失比例的缺失图和重建图如图3所示.

图3 不同缺失比例的缺失图和重建图

不同缺失状态下的重建结果如表1所示,程序的平均运行时间约为125 s,这证实了算法的有效性.在输入数据大小一定的情况下,剪切尺度参数的选择十分重要,如果剪切尺度过大,会对图像复原结果产生振铃现象.

表1 不同缺失状态下的重建结果

2.3 剪切波实现不同方式实验对比

为了验证基于剪切变换处理凸集映射图像的效果,我们采用了图像金字塔模式进行频域实现,并将结果与时域方法进行比较,不同剪切波实现方式重建结果如图4所示.当图像缺失状态达到50%时,采用剪切变换处理的图像重建效果要比图像金字塔模式处理的效果好.这主要是因为图像金字塔模式经过傅立叶级数展开后,选取有限项进行合成,由于不连续点的周期函数的存在,合成波形中出现峰值,这在图像上表现为振铃效应,它大大降低了图像的质量.此外,基于图像金字塔模式的计算复杂度高,采用频域和时域两种方式恢复图片的结果如表2所示,但此时运行时间较长,达到了368.2 s.相反,剪切变换处理的数据冗余量较少,运行时间只有91.48 s.综上所述,本研究提出的时域实现剪切变换的数据算法是可行的.

图4 不同剪切波实现方式重建结果

表2 采用频域和时域两种方式恢复图片的结果

3 结语

本研究通过傅立叶变换和伪极网格坐标系变换的实验,验证了离散剪切变换对图像数据恢复的有效性,恢复后的图像轮廓和纹理表达非常清晰.之后对比了剪切变换的不同实现方式(时域和频域)对缺失50%的图像数据重建质量的影响.结果表明: 基于时域的剪切变换数据算法是可行的,数据冗余较少,运行时间较短,重建后的图像质量较好.