基于神经网络的快速识别手写数字研究

张 博,何小利,龙 源,余 谦,邹显迪

(四川轻化工大学 计算机科学与工程学院,四川 宜宾 644005)

0 引言

手写数字识别一直是人工智能和计算机视觉研究的热点,该技术可以应用于邮政编码和数据报表等领域,从而提高手写数字数据化的效率.研究一种具有扩展性、高效且准确的手写数字识别方法具有重要意义[1].

根据字体分类,数字识别可以分为印刷体识别和手写体识别两类.手写体识别按照识别时间分类,又可以分为联机手写体识别和脱机手写体识别两种模式[2].本研究主要研究脱机手写体识别,其需要将手写数字图片规范化,并使用卷积神经网络(Convolutional Neural Networks,CNN)模型进行训练.在图像处理和分类领域中,卷积神经网络一直都以优良的表现占有一席之地[3].阿拉瓦特等验证了超参数的微调对提高卷积神经网络结构的性能至关重要,特别是增加CNN结构中的卷积层数对手写体数字识别性能的影响较明显[4].在机械领域中,卷积神经网络及其衍生网络被应用于磨屑自动分类,构建以人工神经网络(Back Propagation Neural Networks,BP)为一级分类、六层卷积神经网络为二级分类的BP-CNN模型,该模型缓解了普通神经网络对磨屑识别效率低、准确度表现不好、多种特征需要高价值机器才能识别的问题,最终识别率能够达到80%以上[5].

深度卷积神经网络(Deep Convolution Neural Network,DCNN)是一种结合深度学习构建卷积神经网络的技术,其主要作用是将数据的底层特征以一定规律组合,并抽象成高层特征.虽然这项技术广泛应用于图像学习视觉特征提取,但是它也存在一些缺点,如网络结构复杂,需要大量的标记数据集和高计算资源.本研究基于DCSOM(Deep Convolution Self-Organizing Maps)模型[6],采用主分量分析(Principal Component Analysis,PCA)特征提取方法,重构神经网络,实现了快速识别手写数字的方法.

由于BP神经网络具有强大的非线性映射能力和柔性的网络结构,而卷积神经网络具有表征学习的能力,因此将两者的优势结合起来,构建一种BP-CNN神经网络,可以高速搜索最优解,缓解优化学习速度和精确度之间的矛盾.具体改进思路如下.第一,在使用梯度下降时,如果梯度函数的斜率为正,则增加下一个梯度值,如果函数斜率为负,则减小下一个梯度值; 第二,采用迭代方式,通过不断优化目标、目标所依赖的变量以及变量之间的约束关系来构建和优化模型.

1 BP-CNN的建立

1.1 构建传统模型

卷积神经网络的模型通常采用传统的卷积层、池化层和全连接层的方式构建.其中卷积层和池化层结合在一起,主要起到提取图像特征的作用.它们在获取图像典型特征图的同时,减少了输入层到全连接层中的数据量.模型的构造过程如下: 首先,手写数字图像通过一个激活函数为ReLU的32个3×3二维卷积层; 其次,通过一个2×2的池化层、Flatten层和一个Softmax全连接层; 再次,输出由10个神经元构成的识别结果.Flatten的主要功能是将卷积层输出的数据展开后输入下一层的全连接层.

1.2 构建BP-CNN模型

在卷积神经网络中,卷积核的大小代表感受野的大小,而卷积核的步长度则代表提取的精度.第一层由9个大小为4×3、步长为(2,1)的卷积核构成,输入图像的大小为28×10像素,经过该层以后输出为13×8像素; 第二层由18个3×3大小、步长为(2,1)的卷积核构成,将上一层神经网络的输出作为该层卷积层的输入,经过神经网络卷积以后得到输出值为6×6像素的图片; 第三层采用全连接层,数据的输出维度为20×20像素大小; 第四层经过Flatten层对数据进行展平,最终通过全连接层得到10个输出神经元.

基于以上对模型的描述,BP-CNN模型的结构图如图1所示.其中卷积层和全连接层作为神经网络结构的隐藏层,对输入的数据进行卷积和筛选操作以后,得到最终的10个结果.

图1 BP-CNN神经网络结构示意图

2 重构神经网络的过程

2.1 数据维度压缩

MNIST数据集包含70 000张图片,分别有60 000张图片的训练集和10 000张图片的测试集,本研究使用已经处理好的28×28像素的数值为0—9手写数字集.我们使用K折交叉验证的方法,将训练集和测试集随机混合后,使用K折交叉验证来选择第一个模型准确率最高的K值,以对训练集和测试集进行分割.我们将图像数据放大255倍,并将图像标签从数字转化为1×10的矩阵,明确神经网络输出层的神经元表达的意义.对于基础的MNIST手写数字识别,我们可以使用逻辑回归的方法,将数字部分识别为1,黑色部分识别为0,并直接使用逻辑回归模型进行预测.但是这种方法只能实现简单的预测,其准确率不如神经网络模型.

在BP-CNN模型中,我们采用了两种降维方法: PCA和等度量映射(Isometric Mapping,ISOMAP).

在主成分分析法中,对于样本X∈Rp×p,每个样本都有p×p个维度的属性.存在降维矩阵矩阵A,满足A∈Rm×p,可得到Axi为降维后的样本.降维的关键点在于找到满足约束条件的m维和保证降维合理化的矩阵A,标准化矩阵如下:

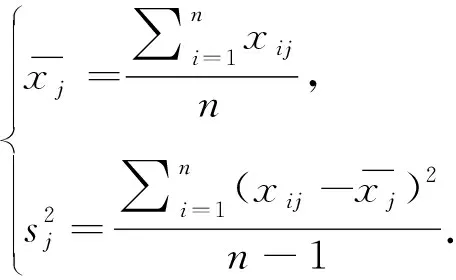
(1)

(2)

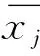
标准化阵Z求相关系数矩阵如下:

(3)

其中,rij是标准化阵,样本相关矩阵R通过标准化阵和样本x的计算,使用标准化阵Z和维度n来表示.样本相关矩阵R的特征方程为:

(4)

(5)

每一个标准化的变量即为主成分,m×p维度的最大主成分矩阵降维后矩阵Uij的公式如下:

(6)

2.2 重构神经网络模型公式

重构神经网络模型的工作原理如下: 首先,由卷积神经网络对图像特征进行提取; 然后,通过人工神经网络使用随机梯度下降方法来更新网络中的参数,以减少人为操作带来的影响; 之后根据PCA-MNIST数据集的特点和性质,对神经网络模型进行微调,以判断模型是否达到设计的迭代次数,并计算各层之间的精确度和误差值之和,以及记录训练时间进行对比分析; 最后,通过输出值来对隐藏层和输出层之间的权重进行调节.该输出值是通过ReLU激活函数计算而来的.隐藏层第j个神经元的输出值zj和连接第j个神经元和第i个神经元的权重Wji的公式如下:

(7)

(8)

其中,xi为节点i的输入值,yk表示在输出层节点k的输出值.误差E为所有输出层节点的输出值与目标值的误差平方和,其公式如下:

(9)

其中,dk为输出层节点k的目标值(实际值).权重连接值的大小ΔW的公式如下:

(10)

其中,η是学习率,公式含义为权重连接值等于误差E对权重w的导数乘学习率取负值.利用坡度下降学习法调整权重连接值的大小,其调整的幅度取决于学习率η的设定大小.Δwkj为第j个隐藏层神经元与第k个输出层神经元之间的权重公式如下:

Δwkj=-ηδkzj.

(11)

其中,δk为输出层第k个输出神经元的误差量.将δk使用已知的yk和dk来进行表达,得到隐藏层权重的最简表达式如下:

(12)

2.3 学习率自适应

为了减少对人工输入参数的需求,并寻找神经网络模型的最佳学习率,我们使用Keras的随机梯度下降法(Stochastic Gradient Descent,SGD)来实现梯度下降,并作为一个连续衰减的学习率调度器.我们设定初始学习率为0.1,衰减系数为0.001.实验结果显示,这样做大大提高了模型的准确率,同时也降低了模型出现过拟合的风险.在使用自适应的学习速率时,增加动量系数可以在两次梯度下降的方向相同时,加速下降的速度,从而达到更快的收敛.学习率lr的计算公式如下:

(13)

其中,设定初始学习率lr0=0.1,衰减系数decay=0.001,epochs为总迭代次数,epochsi为第i次迭代,一个学习率梯度下降的例子如图2所示,其展示了BP-CNN模型的学习率梯度下降的一个过程.

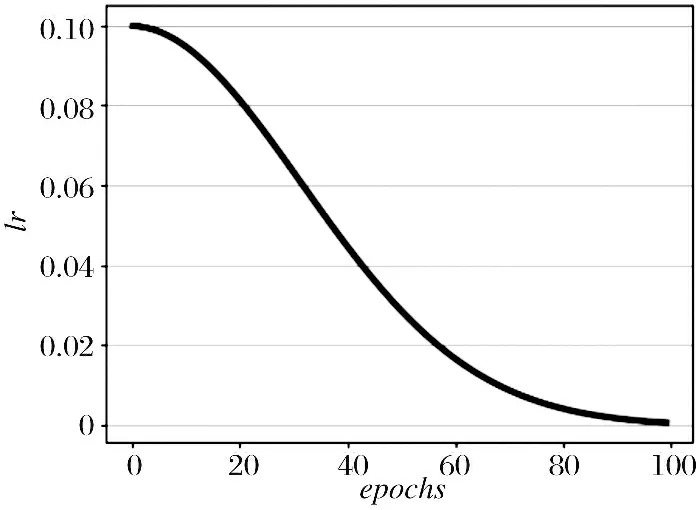
图2 学习率梯度下降

2.4 模型对抗性研究

为了验证模型预测的稳定性,我们向训练集和测试集添加了三种类型的噪声.这些噪声包括高斯噪声、加入了占图像像素点0.1比例的椒盐噪声,以及从原图像中删除了占图像像素点0.03比例的部分像素.我们还采用了相同的随机变换规则,将噪声数据与原始数据混合在一起.这样做有两个目的: 一是减少噪声累积导致的数据特征增多,避免使模型的预测结果出现偏差; 二是检验模型在添加了这三种不同噪声的数据集上是否仍能保持稳定.

3 模型运行和效果评估

我们采用ISOMAP降维方法将每张图片从28×28像素降低到8×8像素.实验结果显示,测试集的效果达到了95%以上,但训练集的效果仅有10%.这可能是由于数据降维处理导致了特征值的异常,或者模型出现了过拟合.为了提高模型的泛化性能,我们采用批量训练法对训练集进行均等分割.实验结果显示: 通过这种方式,准确率从10%提升到了31%,因此可以判断并非过拟合问题.

各模型在数据集上的时间如表1所示.表1展示了三种模型在不同迭代次数和两种数据集上的运行时间分析.

表1 各模型在数据集上的时间

在BP模型、CNN模型和BP-CNN模型在PCA-MNIST数据集中迭代30次的精确度趋势方面,BP神经网络的精确度和损失与其他模型相比较表现较差.BP-CNN模型的初始表现较差,但其精确度提升速度较快,从第六次迭代开始,BP-CNN模型的精确度要比传统BP和CNN模型略高.使用重构神经网络的目的是降低使用PCA降维方式对网络精确度带来的影响.对模型选取不同的迭代次数,当模型训练次数epochs>=5时,模型训练的准确率提升速度逐渐降低.

使用混淆矩阵的方法对模型训练结果进行分析,其模型混淆矩阵分析图如图3所示.该分析目的是评估训练模型对哪些数字的识别准确率较高,以及哪些数字更容易混淆.横纵坐标分别表示模型预测的标签值和图片原始标签值,对角线元素是不同目标的正确识别数量,其余元素为识别错误的情况,背景颜色的深浅代表该数字占总数字的比率.三种模型对数字1的识别灵敏度高,对数字5的灵敏度低.BP模型将数字5错误地识别成3的概率最高,为16.2%.BP-CNN与CNN的识别效果相近,与它们的精确度相似符合.由此可得,重构神经网络模型在识别数字3和数字5中最容易出错,由于两个数字的相似度较高、像素分布比较相似,可以在后续研究中建立两个数字独特的特征点进行区分.最后,对原始数据加入一定量的高斯噪声和椒盐噪声,测试模型的稳定性.通过实验结果发现,高斯噪声带来的影响比椒盐噪声的影响要大,因为高斯噪声是对每张图片的所有像素点都进行了处理,增大了模型识别图片的特征值,最终导致模型面对噪声数据识别困难.但是BP-CNN模型在多重组合噪声影响的情况下精确度依旧有88%.对比没有噪声影响的准确率相对误差在5%以内,体现噪声对重构模型的影响能力有限.

图3 模型混淆矩阵分析图

4 结论

与传统的数字识别算法相比,BP-CNN具有运算速度快、运行参数少的优点.因此,它被用于重构卷积神经网络模型,可以减少网络产生的参数量.在运行过程中,BP-CNN模型总共产生了9183个神经元,远少于全连接层神经网络或卷积神经网络的神经元个数.当模型运行于PCA-MNIST数据集时,BP-CNN模型的精确度降低到91.1%,但仍优于传统神经网络.与在MNIST数据集上相比,它缩短了40%的时间,证明了通过对数据模型进行降维并使用重构的神经网络模型,可以大大提高模型的运行速度.

该模型在运行时间和稳定性方面优于传统模型.例如,如果将其应用于车站、飞机场和渡口等人流量较大的场所,它能够很大程度地提高检票闸机的运行速率和人流通行速率,并减少客人等待时间较长或发生拥挤踩踏事件的风险.此外,该模型也可以快速有效地读取车站中普通民众的银行卡或身份证等文字信息,以减少系统判断的过程和时间.重构模型BP-CNN对图片规范化的数据要求比较高,未来可以在车站等场景中随机截取数字进行测试,加入更多的噪声数据和影响因子,以提高模型的广泛适用性.