多因素下尾砂充填料浆流变参数试验研究及预测分析①
刘金枝, 殷 菲, 高子明
(上海海洋大学 信息学院, 上海 201306)
近年来,膏体充填技术以其安全、高效、环保以及经济等优势得到广泛应用[1]。 膏体材料的流变特性对膏体充填效果影响巨大。 关于膏体材料流变特性方面的研究多针对特定工程案例[2-6],得到的流变参数很难具有普适性[7]。 随着机器学习应用研究逐渐兴起,将机器学习应用在预测复杂的流变特性研究方面具有很大的实际意义[8-10]。 本文通过试验探究不同影响因素对膏体屈服应力和黏度的影响,记录不同影响因素下的流变特性,并进行数据拟合得出其影响程度大小,分析其影响流变特性的原理。 控制料浆质量浓度、灰砂比、级配和温度等变量进行试验并基于机器学习对多因素影响下的流变特性进行预测,并验证其预测准确性。
1 试 验
试验采用与文献[1]相同的试验材料及试验装置,充填材料化学组成如表1 所示。 考虑到膏体流变特性受物料组成及颗粒级配影响,试验采用的全尾砂粒径绝大多数在100 μm 粒级以下,全尾砂粒径分布如图1 所示。 采用Brookfield R/S+型流变仪测量膏体料浆流变特性相关数据。
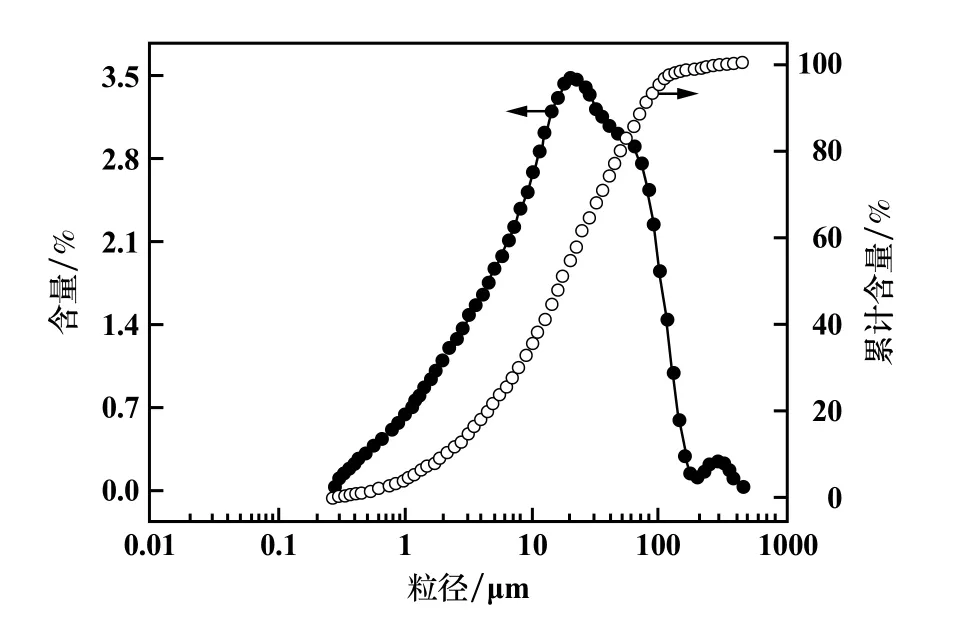
图1 全尾砂粒径分布

表1 充填材料化学组成(质量分数) %
配置浓度配比分别为62%、64%、66%、68%、70%和72%,灰砂比分别为1 ∶4、1 ∶8和1 ∶16 的膏体料浆,探究浓度和灰砂比对流变特性的影响,试验均在室温下进行。
配置浓度配比分别为62%、68%和72%,灰砂比分别为1 ∶4和1 ∶16 以及破碎时间分别为0 s 和40 s 的膏体料浆,将试验得到的流变参数结果作为样本集来预测料浆的屈服应力与黏度,从而对多因素影响下的流变参数进行预测研究与分析。
2 试验结果与分析
2.1 料浆浓度与灰砂比对屈服应力的影响
灰砂比1 ∶4、不同料浆浓度下,以及料浆浓度72%、不同灰砂比下膏体屈服应力随时间变化(剪切速率0.05 s-1)如图2 所示。 由图2 可知,尾砂料浆屈服应力随着剪切时间增加大致可以划分为3 个阶段:线性增长阶段、缓慢减小阶段及基本稳定阶段。 在线性增长阶段,屈服应力随着时间增加表现出不断增大的趋势,其原因是尾砂料浆内部存在大量网状结构,这个阶段屈服应力仍不足以破坏网状结构,导致屈服应力不断增大;在缓慢减小阶段,屈服应力随着时间增加逐渐降低,其原因是尾砂料浆内部网状结构逐渐被破坏,屈服应力不断减小;在基本稳定阶段,料浆屈服应力基本保持不变,这是因为料浆内部网状结构完全被破坏,此时的极限应力便是膏体的静态屈服应力,此时料浆开始发生流动。 因此,料浆屈服应力的变化与料浆内部网状结构存在明显的关系,浓度越高的料浆越容易形成更为致密的网状结构,宏观上表现为屈服应力峰值随着浓度增加而不断增大。

图2 室温下屈服应力随时间的变化
图3 为尾砂料浆屈服应力随料浆浓度和砂灰比的变化特征。 从图3 可以看出,料浆灰砂比一定时,料浆屈服应力随着浓度增加表现出指数函数的递增规律,且灰砂比越高的料浆屈服应力增加得更显著。 高浓度尾砂料浆意味着颗粒间的间距较小,更容易形成稳固的网状结构,需要更高的应力才能完全破坏网状结构,因此料浆屈服应力表现出不断增大的趋势。 料浆屈服应力随灰砂比的变化曲线与料浆浓度的参数水平具有显著的相关性,具体表现为:料浆浓度62%和64%时,料浆屈服应力随着灰砂比增大基本保持不变,说明对于低浓度尾砂料浆,水泥含量对屈服应力的影响是十分有限的;料浆浓度70%和72%时,料浆屈服应力随着灰砂比增大而增大,且在灰砂比从1 ∶8增加至1 ∶4时,料浆屈服应力增加更为显著,说明水泥含量对尾砂料浆屈服应力的影响与料浆浓度的参数水平具有显著的相关性,表现为水泥含量对屈服应力的影响程度随着料浆浓度增加而增大,侧面反映出灰砂比对屈服应力的影响程度低于料浆浓度对屈服应力的影响程度。
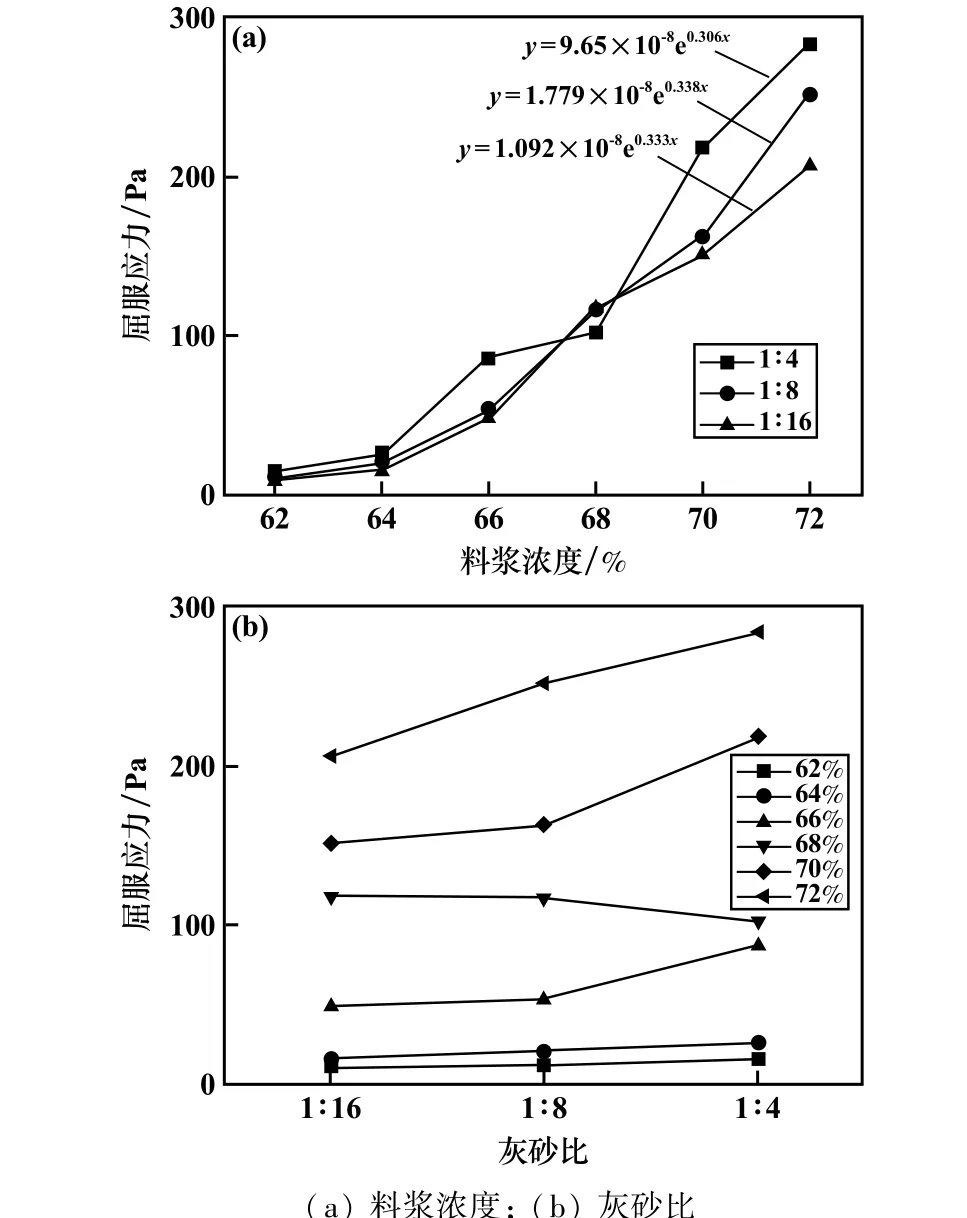
图3 屈服应力随料浆浓度和灰砂比的变化
2.2 浓度与灰砂比对黏度的影响
不同料浆浓度与灰砂比下黏度随剪切速率变化(剪切速率由0 s-1线性增加至60 s-1)如图4 所示。 由图4 可知,料浆流变特性中表征黏滞性的黏度在较低剪切速率下随剪切速率上升出现剪切稀化的特征,且大致分为3 个阶段:快速减小、似线性减小和保持稳定。 在快速减小阶段,黏度随着剪切速率增加表现出迅速减小的趋势,原因在于初始黏度较大,尾砂料浆内部那些比较散乱、无序粒子受到流层之间的剪应力作用,减少了它们的互相钩挂,会发生滚动旋转进而收缩成团,于是表现为剪切稀化的现象;在似线性减小阶段,黏度随着剪切速率增加继续降低,原因在于尾砂料浆内部结构破坏程度慢慢减小,黏度也随着破坏程度减小而缓慢减小;在保持稳定阶段,料浆内部结构基本保持稳定,黏度也基本保持稳定。 整个过程都伴随着料浆内部结构的破坏、分散、聚集和再分散。
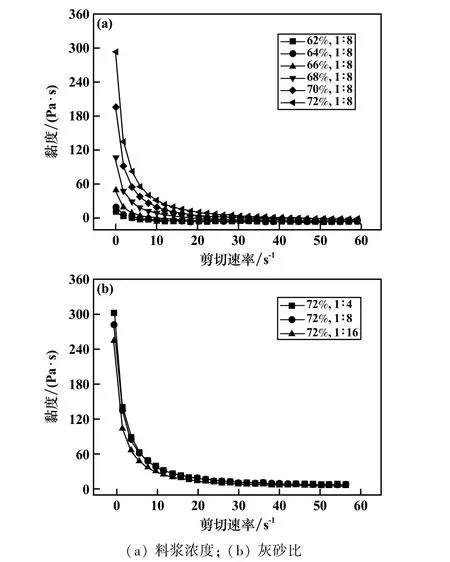
图4 室温下黏度随剪切速率的变化
根据Brookfield R/S+型流变仪得到的试验数据,黏度取平均黏度,即剪切时间内黏度的算术平均值,可得黏度随料浆浓度和灰砂比变化如图5 所示。 由图5可以看出,料浆灰砂比一定时,料浆黏度随着料浆浓度增加表现出指数函数的递增规律,且灰砂比越高的料浆黏度增加得更显著。 料浆黏度随灰砂比的变化曲线与料浆浓度的参数水平具有显著的相关性,具体表现为:料浆浓度62%~68%时,料浆黏度随着灰砂比增大基本保持不变,说明对低浓度尾砂料浆,水泥含量对黏度的影响十分有限;料浆浓度70%时,黏度随灰砂比增加显著增加然后增速变缓;料浆浓度72%时,料浆黏度随着灰砂比增大先变化不明显、后缓慢增加,说明水泥含量对尾砂料浆黏度的影响与料浆浓度的参数水平具有显著的相关性,表现为水泥含量对黏度的影响程度随着料浆浓度的不同而不同,侧面反映出灰砂比对黏度的影响程度低于料浆浓度对黏度的影响程度。
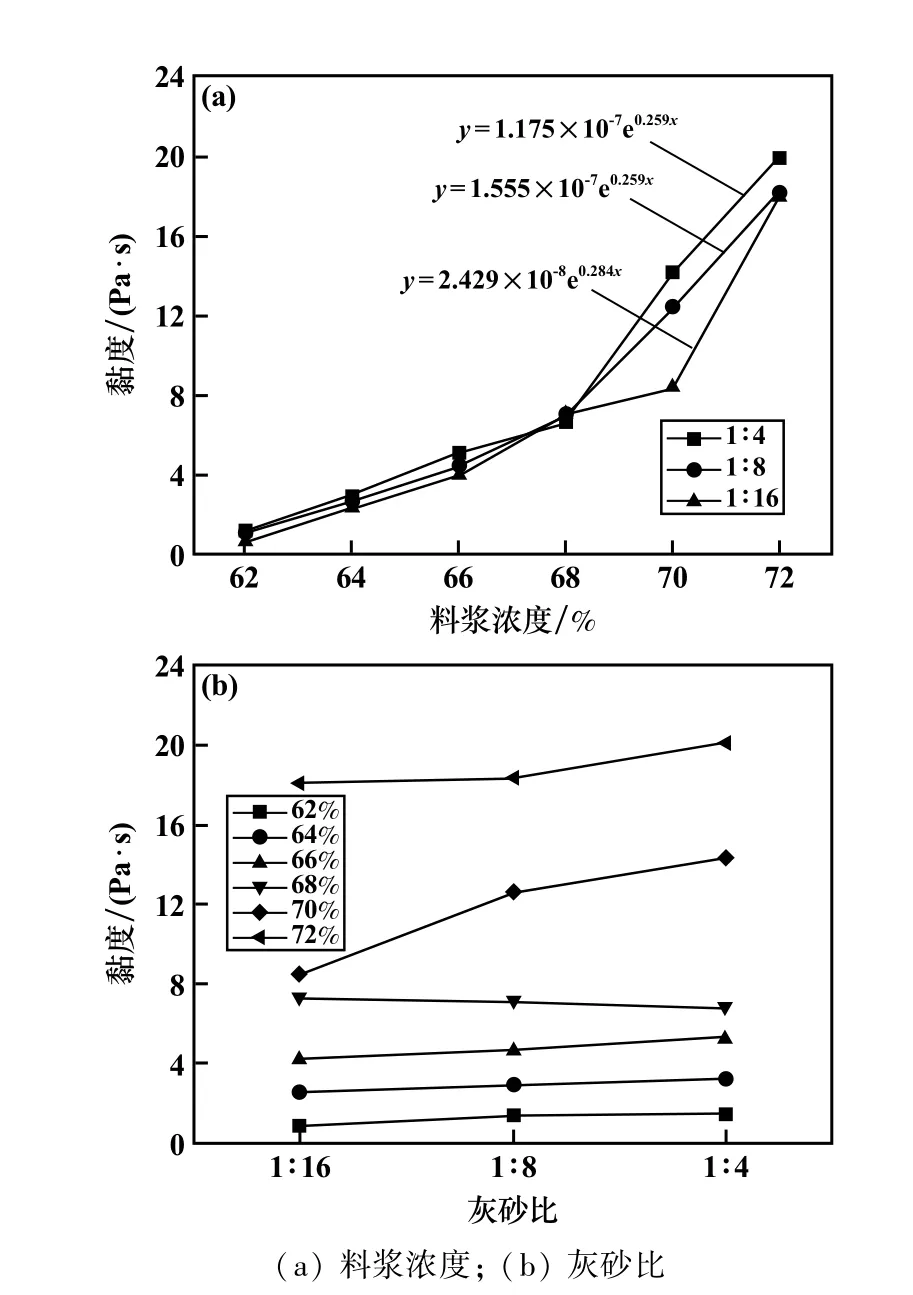
图5 黏度随料浆浓度和灰砂比的变化
3 多因素条件下流变参数预测分析
3.1 XGBoost 介绍
XGBoost(Extreme Gradient Boosting)是一种高效的梯度提升决策树算法[11],它在原有GBDT 基础上进行了改进,使模型效果得到大大提升。 作为一种前向加法模型,它的核心是采用集成思想——Boosting 思想,将多个弱学习器通过一定的方法整合为一个强学习器,即用多棵树共同决策,并且每棵树的结果都是目标值与之前所有树的预测结果之差,并将所有的结果累加即得到最终结果,以此达到整个模型效果的提升。XGBoost 是一种分布式梯度增强库的优化,它在Gradient Boosting 框架下实现机器学习算法。 XGBoost提供了并行树提升(GBDT 或GBM),诸多数据科学相关的任务可以通过它迅速完成。 在分布式环境(Hadoop,SGE,MPI)下可以运用相同的代码,与此同时,大规模样本案例的问题也可以通过它解决。XGBoost 成功之处在于它可以应用于各种场景,具有很强的可扩展性,其可扩展性归功于几个重要的系统和算法优化。 除此之外,XGBoost 的运行速度较现今大部分解决方案都要快数十倍。 它是一种新型的用于处理稀疏数据的树学习算法,在核外树学习这部分提出了一种有效的缓存感知。 对于并行树的学习可以使用一种新的稀疏感知算法,分布式并行计算还可以加快算法的学习效率,使学习更快,对模型的探索也更快。
3.2 模型预测与结果
条件属性和决策属性是模型预测流变参数的试验因素,其中料浆质量浓度、灰砂比、级配和温度为条件属性,料浆黏度和屈服应力为决策属性。 按照前述试验方案与步骤进行试验,将试验得到的流变参数结果作为样本集。 选取60 组流变数据作为预测模型的样本集,其中75%的数据作为训练集、25%的数据作为测试集。
3.2.1 屈服应力预测结果
屈服应力测量值与XGBoost 模型得到的屈服应力预测值对比结果如表2 所示。
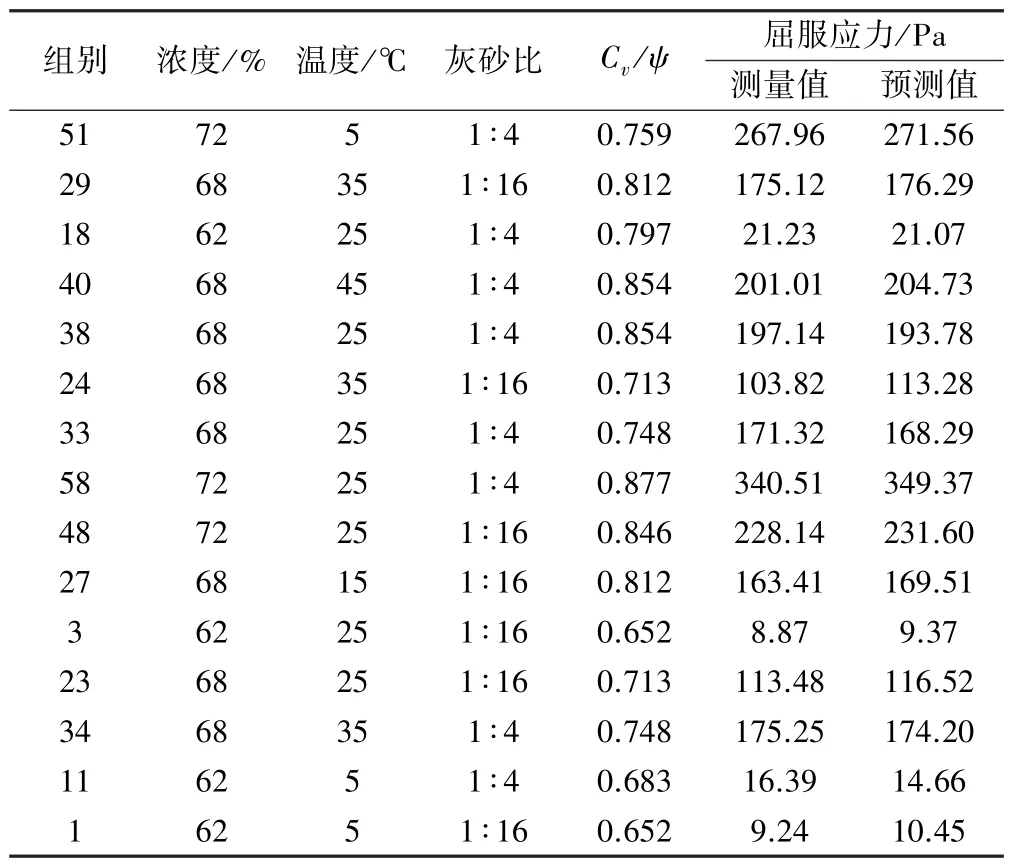
表2 屈服应力测量值与XGBoost 模型预测值对比结果
3.2.2 塑性黏度预测结果
黏度测量值与XGBoost 模型得到的黏度预测值对比结果如表3 所示。
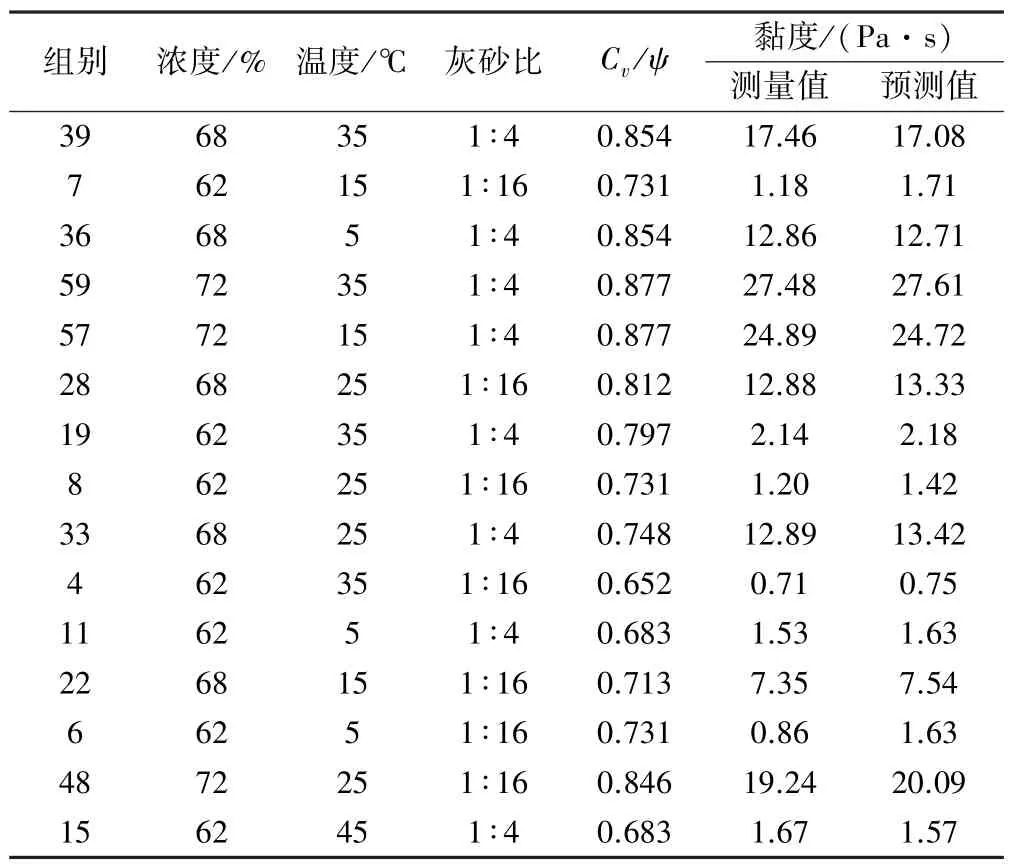
表3 黏度测量值XGBoost 模型预测值对比结果
3.2.3 分 析
膏体料浆质量浓度对于膏体流变特性的影响最强,之后是灰砂比的影响。 料浆浓度低于64%时,灰砂比对膏体流变特性影响甚微。 料浆浓度和灰砂比对料浆屈服应力和黏度的影响本质是对料浆自由水比例的影响,料浆灰砂比的增加使其水化产物增多,但由于是间接影响自由水的比例,屈服应力和黏度随灰砂比增加呈现近似线性增长,而料浆浓度直接影响自由水比例,屈服应力和塑性黏度随料浆浓度增加表现为指数增长。
使用XGBoost 这种高效的梯度提升决策树算法,对料浆流变参数进行预测,得到的预测值与实际值十分接近。 控制料浆质量浓度、灰砂比、级配和温度等变量进行试验,将试验得到的流变参数结果作为样本集,屈服应力预测模型各项误差结果为:RMSE=4.33,MAE=3.36;黏度预测模型各项误差结果为:RMSE=0.40,MAE=0.31。根据经验法则,RMSE值在0.2 ~0.5 之间,说明该模型能够较准确地预测数据。
XGBoost 的基本思想和GBDT 相同,但做了一些优化:比如二阶导数使损失函数更精准、正则项避免树过拟合、Block 存储可以并行计算等。 使用XGBoost 模型预测膏体在多因素条件下的流变参数可以得到较高的精度。 可以看出,使用该模型误差较小,拟合程度高,能满足实际生产对预测分析的要求。
4 结 语
采用Brookfield R/S+型流变仪对某尾砂制备的充填料浆进行了流变特性测试,并采用XGBoost 算法对料浆流变参数进行了预测。 结果表明,室温条件下,膏体料浆质量浓度对膏体流变特性的影响强于料浆灰砂比,料浆浓度低于64%时,灰砂比对流变特性影响较小;料浆浓度增大,料浆屈服应力和黏度呈指数增长,料浆浓度68%时增长最快;料浆灰砂比增大,料浆屈服应力和黏度呈近似线性增长。 XGBoost 预测结果与实际值的相对误差以及均方差均在合理范围内,证实该模型对预测料浆流变参数具有一定的准确性。

