基于CFD-DEM 的气力输送变径管中颗粒流动特性分析①
侯艳君, 王庆辉, 周甲伟, 闫翔宇, 郑泽冰, 刘晓辉
(1.华北水利水电大学 机械学院,河南 郑州 450045; 2.长安大学,陕西 西安 710064)
采矿后矿山会形成地下采空区,存在地表塌陷的风险[1]。 目前常采用充填法向矿山采空区中充填岩石、矸石、炉渣等材料来实现对采空区顶板岩层移动的控制,进而达到废物利用以及减弱地表沉降的目的[2-3]。
基于气力输送技术的气力充填具有良好的密闭性、灵活性以及较高的自动化程度,被广泛应用于采空区充填过程。 但受地形或空间的限制,长距离(1~2 km)输送大量散装物料的需求一直在增加,在这种情况下,通常采用长距离高压气力输送系统。 长距离气力输送系统主要由气源机械、仓泵、输送管道和旋风分离器组成[4]。 在常规管道和高压条件下,由于气体的可压缩性,管道末端的气体和固体速度很高,会导致颗粒破碎、管道磨损以及较大的压力损失和较大的能量损耗。在该系统中,可以使用变径管代替常规管道[5]。 变径管可以通过适当增大管径来降低气体速度,从而进一步降低压降,减少系统能耗[6-9]。
以往对变径管的研究大多集中于变径管中压降的变化规律及影响因素[10-12],很少深入研究变径管本身几何结构的变化对管道中气固两相流流动特性的影响。 本文从变径管几何结构参数入手,采用CFD-DEM耦合方法研究变径比和变径长度对变径管中气固两相流流动特性的影响规律,为变径管的设计提供参考。
1 数学模型
在CFD-DEM 模型中,两相控制方程分别用于求解两相中的物理量,其中气相由CFD 进行求解,颗粒相由DEM 进行求解。
1.1 气相控制方程
在CFD-DEM 模型中,气体被视为连续化,遵循Navier-Stokes 方程,采用连续方程和动量方程进行求解,求解时假设压降由气相和颗粒相共同分担[13]。 连续方程也称为质量守恒方程。 该定律可表述为:单位时间内流体微元体中质量的增加,等于同一时间间隔内流入该微元体的净质量[14]:
式中ρg为气体密度,kg/m3;ug为气体速度,m/s;t为时间,s。
动量守恒定律可表述为:微元体中流量的动量对时间的变化率等于外界作用在该微元体上的各种力之和。 该定律实际上是牛顿第二定律:
式中p为气体压力,Pa;τg为气体黏度,m2/s;g 为重力加速度,m/s2;S为动量守恒方程的广义源项,对于黏性为常数的不可压流体,S=0。
1.2 颗粒相控制方程
在CFD-DEM 模型中,颗粒被视为离散相,由离散单元法根据牛顿运动定律进行求解。 颗粒i在任意时刻t的控制方程可描述为:
颗粒的受力包括重力mig、气固相互作用力fp-g,i和接触力fcontact,ij。 式中mi为颗粒质量,kg;Ii为转动惯量,kg·m2;vi为颗粒速度,m/s;ωi为角速度,rad/s;ki为与颗粒i发生接触的颗粒的数量;Tij为扭矩。
2 模拟方法验证及模拟条件
本文主要采用Fluent-EDEM 耦合数值模拟方法进行研究,为了验证本文所用模拟方法的可靠性,采用与文献[12]一致的边界条件和参数进行模拟对比,具体参数如下:竖直圆管长3 m、直径53.4 mm,底部为入口,颗粒为直径2.85 mm 的球形颗粒,材料密度2 500 kg/m3,质量流率0.119 kg/s,颗粒入口速度3 m/s,入口气速25 m/s,出口类型为压力出口,出口压力为0。 对数值模拟结果分析得到该管道的单位管长压降为333 Pa/m,与文献[12]的数据320 Pa/m 仅相差4.1%,由此可证明本文所用数值模拟方法准确。
变径管几何结构如图1 所示。 该管道前半部分直径D1为75 mm,通过改变后半部分管径D2来控制变径比,中间是管径逐渐扩张段,变径长度为L,管道总长为3 m。
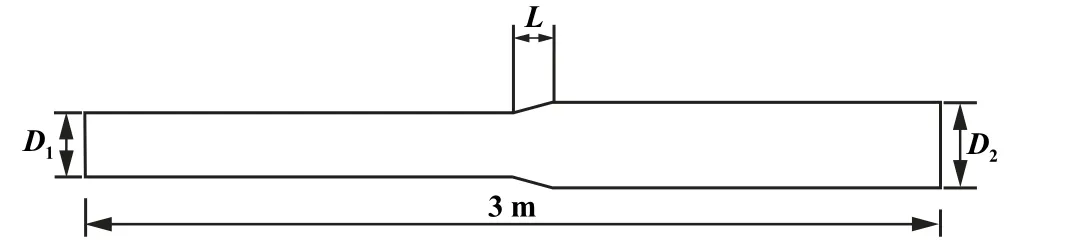
图1 变径管几何结构示意
为了研究变径比和变径长度对气力输送中变径管内颗粒流动特性的影响,采用Fluent-EDEM 耦合数值模拟方法对5 条几何参数不同的变径管以及1 条直径75 mm 的普通直管进行了数值模拟,5 条变径管的几何参数如表1 所示。 管道入口边界条件为速度入口,使用空气作为气相,气相速度30 m/s,固相为半径2 mm 的球形颗粒,颗粒粒径均匀分布,材料密度1 200 kg/m3,颗粒入口速度7 m/s;出口边界条件为压力出口,出口压力为0。

表1 变径管几何参数
3 结果与讨论
3.1 变径长度和变径比对颗粒速度的影响
3.1.1 管道长度对颗粒速度的影响
对于水平气力输送,输送管道和其他与物料接触部件的过度磨损、易碎物料的损坏,甚至输送管道中的堵塞等都与颗粒的速度直接或间接相关。 图2 为直管与变径管的颗粒速度随管道长度的变化对比。 从图2可以看出,在管道前半段,变径管和普通直管中的颗粒速度随着管道长度变化的趋势基本相同,0 ~0.75 m段,颗粒速度呈逐渐增加的趋势,这是因为入口颗粒速度远小于入口气体速度,在该管段,空气对颗粒有一定的加速作用,直到0.75 m 处,颗粒在管道中向前运动的同时受重力作用会向管道底部沉积,管道底部的颗粒速度较低,从而造成0.75 ~1.2 m 段颗粒速度有所下降。 1.2 m 之后,不同管道中颗粒速度的变化趋势产生了巨大的差异:普通直管中颗粒速度逐渐增加,在管道出口处增加到最大,为11.61 m/s;变径管在1.5 m处管径变大,使得管中1.2 ~1.9 m 段的颗粒速度基本不变,从1.9 m 处开始,颗粒速度逐渐减小,在管道出口处颗粒速度减小到8.98 m/s,与普通直管相比,变径管出口处的颗粒速度下降了22.65%。 变径管可以有效降低管道中的颗粒速度。

图2 颗粒速度随管道长度的变化
3.1.2 变径长度对颗粒速度的影响
变径长度对颗粒速度的影响如图3 所示。 从图3可以看出,不同变径长度的变径管中颗粒速度随管道长度的变化趋势基本相同,但变化幅度不同,在0.75 m之前,颗粒在空气的拖曳作用下速度逐渐增加,0.75 m处,变径管2 和变径管3 颗粒速度基本一致,都大于变径管1 中的颗粒速度。 0.75~1.2 m 段,颗粒逐渐向管道底部沉积,颗粒速度逐渐减小,之后随着堆积完成,颗粒速度逐渐增加,可以看到,变径长度越短,增加幅度越小。 这是因为变径长度短,管径变化较快,颗粒速度减小抵消了颗粒速度的增加。 此外,变径之后,3 条管道中的颗粒速度都随管道长度增加而减小,其中变径管1出口的颗粒速度最小,为8.44 m/s,其次是变径管3,为9.32 m/s,变径管2 的颗粒速度最大,为9.47 m/s,说明随着变径长度增加,变径管中颗粒速度先增加后减小。

图3 变径长度对颗粒速度的影响
3.1.3 变径比对颗粒速度的影响
变径比对颗粒速度的影响如图4 所示。 从图4 可以看到,0.75 m 之前,入口处颗粒速度小于气体速度,颗粒在空气的拖曳作用下速度快速增加,一直到0.75 m处,变径管4 和变径管5 的颗粒速度基本一致,都大于变径管1 中的颗粒速度。 0.75 ~1.2 m 段,颗粒逐渐向管道底部沉积,颗粒速度逐渐减小,直到1.2 m 处,颗粒堆积完成,颗粒速度开始逐渐增加,之后直到变径完成,颗粒速度开始下降,在管道出口处达到最小值。 其中变径管1 出口处颗粒速度最小,为8.44 m/s,其次是变径管5,出口处颗粒速度为8.98 m/s,变径管4 的出口颗粒速度最高,为9.32 m/s,这表明随着变径比增大,变径管中颗粒速度先增大后减小。
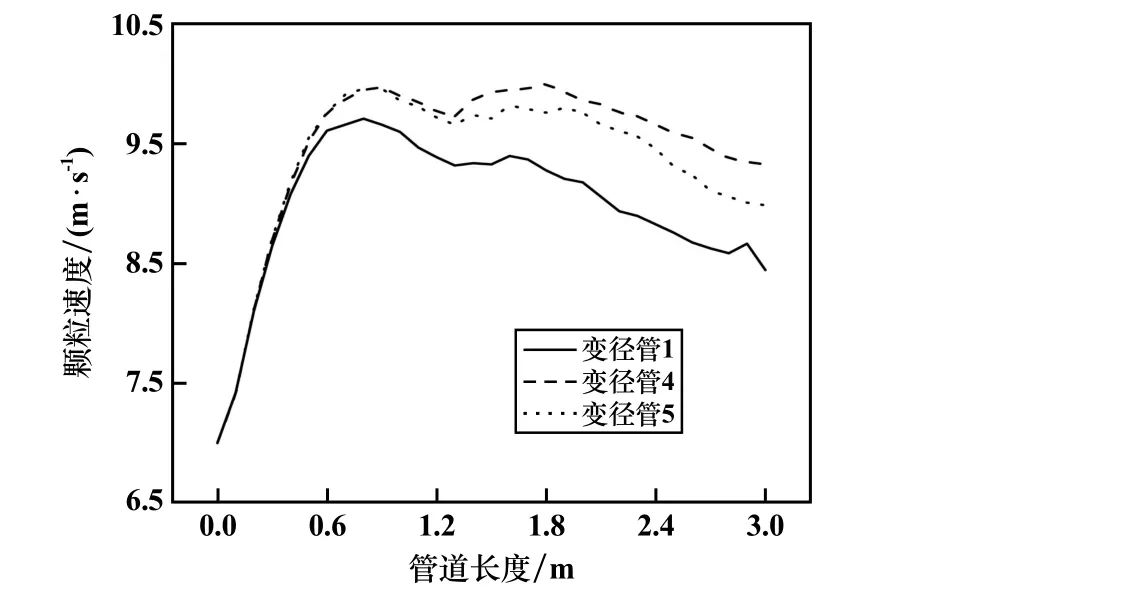
图4 变径比对颗粒速度的影响
3.2 变径长度和变径比对管道压降的影响
3.2.1 管道长度对管道压降的影响
直管与变径管中管道压降随管道长度的变化曲线如图5 所示。 从图5 可以看出,管道压降整体呈现随着管道长度增加而增加的趋势,在管道出口处达到最大值,0~0.6 m 段,2 种管道的管道压降升高幅度都很大,且增加趋势非常相似,这是由于入口颗粒速度小于入口气体速度,气体对颗粒有加速作用,气体压力转化为颗粒的动能,造成一定的加速压损。 在这之后,普通直管中的管道压降随着管道长度增加呈线性增加的趋势,而变径管的管道压降随管道长度的变化趋势可以分为三个阶段:0.6 ~1.5 m 段,颗粒被加速到最大速度,压力不再被转化为颗粒动能,没有了加速压损,压降增加幅度大大减小;1.5 ~1.65 m 段为管道变径段,此处由于管径变化,产生了一定的局部压损;1.65~3.0 m段管道变径完成,管径增大,气体密度减小,使得气体速度与颗粒速度都有所降低,压降增加的幅度更小。直管中的总压降为9 406 Pa,变径管中的总压降为3 562 Pa,相比直管压降下降了62.13%。 此外,从图中也可以直接看出,变径管可以有效降低管道压降,尤其是在变径后效果更明显。

图5 直管与变径管的管道压降随管道长度的变化
3.2.2 变径长度对管道压降的影响
变径长度对管道压降的影响如图6 所示。 从图6可以看出,3 条管道中的管道压降都随着管道长度增加而增加,0~0.6 m 段,3 条变径管的压力损失增加趋势基本相同,都是由于气相对固相的加速作用产生的加速压损。 由前文分析可知,变径管2 和变径管3 中颗粒速度较高,这两条管道中的加速压损更大。 0.6 ~1.5 m 段,随着气固两相流沿管道的输送,产生了气固两相流的摩擦压损和颗粒群悬浮提升的重力压损等,使得总压损逐渐升高。 1.5 m 处,管径发生了变化,产生了一定的局部压损,此处总压损快速上升。变径完成之后,3 条变径管中的压力损失虽然仍在逐渐增加,但增加幅度明显小于变径前。 总体而言,变径管1 压力损失的增加幅度最小,其次是变径管2,说明随着变径长度增加,变径管管道压降增加。
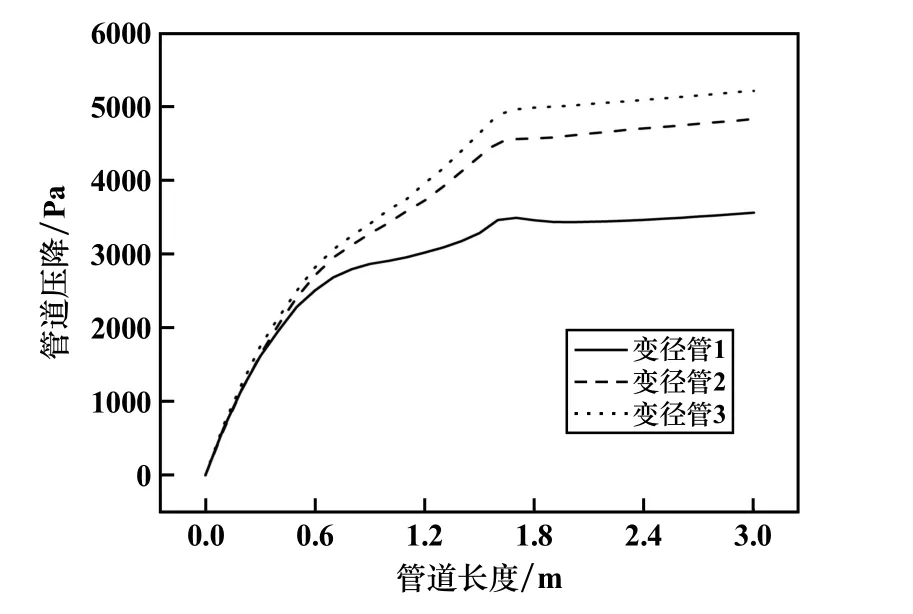
图6 变径长度对管道压降的影响
3.2.3 变径比对管道压降的影响
变径比对管道压降的影响如图7 所示。 从图7 可以看出,3 条管道中的管道压降都随着管道长度增加而增加,其中变径管1 压降最小,其次是变径管4,说明随着变径比增大,变径管中管道压降增大。

图7 变径比对管道压降的影响
3.3 弗劳德数的变化规律
在流体力学中,弗劳德数表示管内流场中惯性力与重力之比,它是一个无量纲数,主要反映了重力对流场中物料流动状态及所受阻力的影响:
式中Fr为弗劳德数;v为气体速度;g 为重力加速度;D为管道直径。
变径管中弗劳德数的变化规律如图8 所示。 可以看到,1.5 m 之前,弗劳德数变化趋势大致相同。 其中,在管道入口处有一个颗粒加速段,离入口距离增加,管内弗劳德数逐渐增大然后逐渐减小至35 左右开始保持不变。 1.5 m 处管径发生变化,弗劳德数也随之产生相应的变化。其中变径管1、变径管2、变径管3 的弗劳德数都降至17 左右,但不同变径长度的下降速度不同。 可以看到,变径长度越长,弗劳德数下降越慢;变径比越大,弗劳德数下降幅度越大。

图8 变径管中弗劳德数的变化规律
4 结 论
采用CFD-DEM 耦合数值模拟方法研究了变径长度和变径比对变径管中颗粒速度、压力损失和弗劳德数的影响规律,并得出了以下结论:
1) 变径管能有效降低颗粒速度。 随着变径长度和变径比增大,变径管中颗粒速度先增大后减小。
2) 变径管能有效降低管道中的压力损失。 增加变径长度和变径比,管道中压力损失均增加。
3) 变径长度不会影响变径后管道中弗劳德数的变化规律,只影响弗劳德数下降速度,变径长度越长,弗劳德数下降越慢;变径比越大,变径后管道中弗劳德数越小。

