复杂流体的屈服应力及其测定与应用
李瑞琪,韦越,郭亚龙,蔡志祥,张洪斌*,郭亨长,姚鹤忠
(1.上海交通大学,化学化工学院,高分子科学与工程系,流变学研究所,上海,200240 2.上海晨光文具股份有限公司,中国轻工业制笔工程技术重点实验室,上海,201406)
1.屈服应力和屈服应力流体
屈服是指材料在受到剪切、拉伸或压缩过程中,当应力(stress)达到某一临界值时,即使只有微小的应力增加,材料的应变(strain)却发生急剧增长的现象。使材料发生屈服时的这一临界应力就是该材料的屈服应力(yield stress)。屈服应力是材料的特性参数,是一个由形变速度、形变温度和形变程度这些参数决定的函数。对于某些非牛顿流体(non-Newtonian fluid),在不受力或所受应力低于屈服应力时能保持形状,不产生宏观流动,表现出类固体(solid-like)行为;只有当应力增大到该流体的屈服应力值时,流体才开始流动,表现出类液体(liquidlike)行为,这样的流体称为屈服应力流体(yield stress fluid)[1]。
屈服应力流体可分为两类:简单屈服应力流体和更为复杂的触变性屈服应力流体[2]。简单屈服应力流体在外应力作用下,其黏度随时间不发生变化,外应力撤除后黏度不可恢复,而触变性屈服应力流体在外应力作用下,其黏度随时间降低,应力撤除后黏度又可逐渐增大。因此,触变性屈服应力流体的黏度变化不仅与所受应力的大小有关,还与应力施加的时间有关[3-5]。
在各类工业领域和现实生活中,屈服应力流体的例子比比皆是,如涂料、牙膏、手霜、唇膏、巧克力、番茄酱、人造奶油、原油、钻井液、油墨、水泥浆体、泥石流、泡沫等均为屈服应力流体。屈服应力流体由于具有独特的流变性质,在化工、石油、食品、制药、化妆品、建筑等诸多领域有着广泛应用[6,7]。
对于屈服应力流体,由于屈服应力的存在,黏度及其在不同条件下的变化还不能完整反映它们在生产加工和使用过程中的流变学性质,对流体屈服应力本身的研究十分重要[7,8]。准确测定屈服应力大小以及全面了解屈服转变前后流体的流变学行为,对于工业生产中产品的设计、性能调控和加工均具有重要的指导意义[7-9]。以牙膏为例,屈服应力的大小是其性能评估的重要指标之一。牙膏要易于从牙膏管中挤出,在不受力或受力较小(小于屈服应力)时,又能维持形状,伫立于牙刷上。因此,在产品设计和实际生产中,牙膏本体的屈服应力需满足牙膏被挤出时易于流动、刷牙时易于铺展,而不受力时又能克服自身重力保持类固体状态的使用要求[3]。
中性笔墨水也是触变性屈服应力流体的一个典型例子。在书写过程中,该类墨水的物理状态经历一个等温可逆的“凝胶-溶胶-凝胶(gel-sol-gel)”转变过程。在书写时,初始态呈凝胶状的墨水在笔头滚珠转动产生剪切应力的作用下,黏度降低并开始流动,呈溶胶状流过笔尖并附着于书写材料表面,而剪切作用去除后墨水黏度又升高呈凝胶状。屈服性和屈服应力的大小还与墨水稳定性以及书写线迹质量、出墨量、静态积滴墨性等书写性能密切相关,也是与笔头匹配的一个重要参数,在墨水配方设计、生产制备、储存和书写性能评估,甚至消费者使用感觉评价中均需详加考量。就墨水在贮存和货架期稳定性而言,屈服应力的存在对确保体系中各种需保持良好分散的填料颗粒不发生沉降、聚集至关重要。墨水的屈服应力等流变学性质需与笔头结构相匹配;反之,笔头设计也需与墨水的屈服应力等流变学性质相匹配。
由于屈服应力流体多是多相多组分的复杂流体,存在复杂多变的多尺度结构,其屈服应力大小通常与许多因素有关,如本体的动态粘弹性、分散相的聚集状态、热历史及剪切历史等,因此屈服应力的准确测定非常困难,从理论到技术手段都处于不断发展中。以下对屈服流体的类别、屈服应力产生的物理机制、屈服应力的流变模型、屈服应力的各种流变测试方法的优势和局限性、屈服应力测定在墨水研究中的应用,以及屈服应力研究中的一些挑战性问题做一简述。
1.1 简单屈服应力流体
简单屈服应力流体没有触变性,其流变学行为只与施加外力大小有关,而与施加时间无关。卡波(Carbopol)[4,5,10]水悬浮液或水凝胶是经典的简单屈服应力流体,常作为模型流体用于该类流体的流变学研究。
卡波是一种聚丙烯酸交联聚合物,分子链上含有大量羧基,是典型的聚阴离子,具有良好的亲水、保水性。卡波能结合大量水分子,链间存在静电排斥作用,在水中易伸展溶胀,形成微凝胶颗粒。这些微凝胶颗粒内部由于存在通过化学键形成的交联逾渗网络,表现为柔软海绵状的类固体性状。在超过一定浓度时,这些微凝胶颗粒紧密堆积在一起,使体系宏观上表现出类凝胶性质。当所受外应力较小时,体系可以保持良好的物理稳定性。卡波是一类非常重要的流变学性质调节剂,有增稠、悬浮、稳定等重要用途,方便易用,已被广泛应用于各类水凝胶、乳液和膏霜中。
图1a显示了卡波水体系(0.1%)在剪切速率(shear rate)升降循环过程中的应力变化情况。可以看到,两曲线完全重合,没有所谓的触变环,表明该体系为简单屈服应力流体,不具有触变性[2]。更高浓度的卡波水体系(1%、3%、5%)也是如此,流动曲线也基本重合[11],表明体系无触变性。
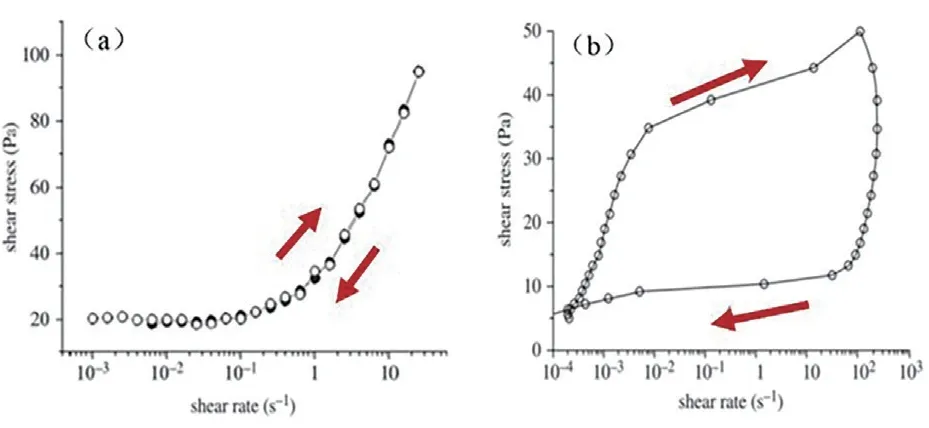
图1 (a)卡波(Carbopol)水凝胶(0.1%)和(b)膨润土(Bentonite)水悬浮体系(10%)的触变环实验结果[2]
1.2 触变性屈服应力流体
与简单屈服应力流体不同,触变性屈服应力流体的流变行为强烈依赖于热历史和剪切历史,其黏度变化同时具有剪切变稀性和时间依赖性两个典型特征。
锂藻土(Laponite)水凝胶和膨润土(Bentonite)凝胶是两类常被用作模型体系的触变性屈服应力流体。锂藻土是一种层状硅酸盐,层面带有大量负电荷,薄层间可通过静电作用形成稳定的网络结构。锂藻土水凝胶是典型的触变性凝胶。在无外力或低外力作用下,其内部网络结构能保持稳定而使体系呈凝胶态,而应力增大致使网络结构被破坏时,则呈现液体性质。若随后将其静置或在低剪切速率下,体系内薄片层又可通过布朗运动使网络结构重新形成,从而恢复其原先的凝胶态。与锂藻土凝胶类似,膨润土凝胶的网络结构是通过膨润土薄层中带负电荷的正面和带正电荷的端面在水中形成卡-房式(House of cards)结构构成的。与卡波水凝胶完全不同(图1a),膨润土悬浮体系有明显的触变环[2](图1b)。由于具有这一独特的触变性质,锂藻土和膨润土常作为触变剂、增稠剂、分散剂、悬浮剂和稳定剂,被广泛应用于精细化工、轻工日化、医药等领域。
需要指出,对于上述提及的卡波水体系,近来有些研究者却发现,在有些制备条件下,卡波水溶液的流动曲线有剪切应力迟滞(shear stress hysteresis)现象[12]。这种迟滞现象被认为是触变性,其产生源于制备时搅拌速率的不同、乳化剂的添加,从而导致卡波微颗粒尺寸的减小,颗粒间产生了耗散作用[10]。这一现象不仅反映出屈服应力流体的复杂性,而且对于多相多组分的复杂流体,如何全面表征屈服应力流体、解释简单屈服应力流体与触变性屈服应力流体的相互转变、合理阐明不同实验的相悖结论,是屈服应力相关研究的一个难点。
1.3 屈服应力的产生机制
根据流体的体系不同,屈服应力产生的物理机制主要有三种:玻璃化转变(glass transition)、堵塞转变(jamming transition)和凝胶化(gelation)。了解这些不同物理机制,有助于认识屈服应力产生的不同本质,更好地服务于产品的设计和加工。
玻璃化转变和堵塞转变是由于体系中颗粒间相互排斥作用产生的。当颗粒的体积分数逐渐增大至某一临界值时,由于颗粒间的排斥作用,颗粒运动范围受限,热运动松弛时间变长,颗粒在外力作用下难以扩散,导致体系产生玻璃化转变。当热平衡松弛时间尺度远远小于外加变形的时间尺度时,体系表现出类固体的行为,则产生屈服应力[13,14]。对于颗粒尺寸较大,可挤压变形的体系(如气泡、乳液液滴),颗粒的布朗运动可以忽略,当颗粒体积分数超过某一临界值时,会导致颗粒之间相互接触而形成紧密结构。这种颗粒之间的互相支撑可使体系达到一个稳定状态,转变成类固体,即发生所谓的堵塞转变,其结果使体系具有屈服应力[15]。这两类流体的屈服应力值与分散相颗粒的体积分数均遵循一定的标度(scaling law)关系。
凝胶化转变则是另一种由于颗粒间相互吸引作用产生屈服应力的方式。当液体体系中颗粒之间相互吸引作用(如强键合作用、疏水作用、氢键等)较大时,颗粒会在体系中形成网络结构,而当这一网络结构具有足够力学强度,能维持体系物理稳定时,就会产生屈服应力[16]。
2.屈服应力的测定
2.1 描述屈服应力流体的经典模型
最理想化的经典屈服应力流体模型是Bingham模型[17](Eq.1)。该模型假设,当对流体施加的外力小于流体屈服应力时,体系呈现类固体性质(可看作黏度无穷大);而当施加的外力大于流体屈服应力时,屈服后的流体呈现牛顿流体的性质,施加应力与屈服应力的差值和剪切速率成正比,可表示为:


图2 各类流体的典型流动曲线比较
实际上,由于Bingham模型过于理想化,现实中的屈服应力流体很少能较好地与之相符合,绝大多数的屈服应力流体在屈服之后都表现出剪切变稀行为,而不是牛顿流体行为。因此,出现了各种基于Bingham模型改进的其他屈服应力流体模型,较常用的有Herschel-Bulkley(HB)模型[18](Eq.2)和Casson模型[19](Eq.3)等。其中广为接受的是HB模型,该模型能很好地描述简单屈服应力流体(如卡波水体系)的流变学行为:
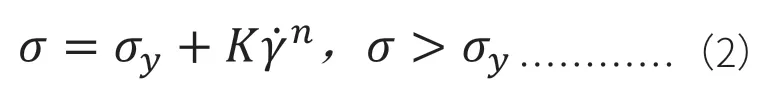
Casson模型[19]是另一种适用于屈服应力流体的模型,其最经典的应用是描述血液的流变学行为[21]。该模型广泛适用于假塑性屈服应力流体,但某些情况下只适用于高剪切速率区域[22]。


图3 可德胶水悬浮液(a:4%、a′:2%、a″:1%)和羧甲基可德胶水溶液(b:6%、b′:3%、b″:2%)应力随剪切速率的变化。右表为所得流变参数值 [20]
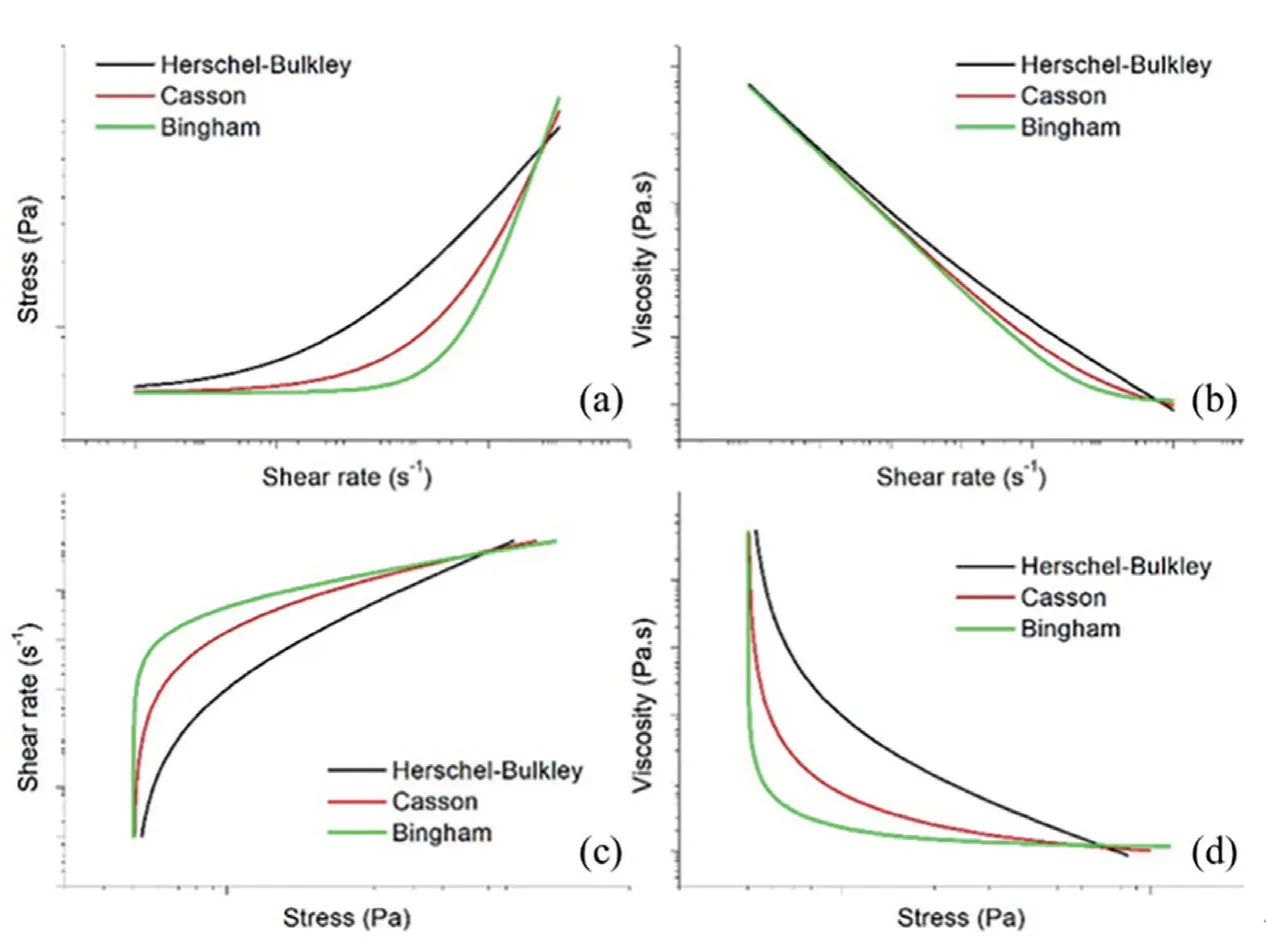
图4 Bingham、Herschel-Bulkley和Casson模型方程所对应的流动曲线
熔融状态的巧克力也是一种典型的屈服应力流体,其流变性质满足Casson方程[23,24]。该模型也能很好地描述天然乳化剂阿拉伯胶(gum arabic)水溶液的屈服性质[25]。
上述三个模型方程所对应的流动曲线,依据不同的参数相互关系,如图4所示。其中图(a)和(b)分别为三种模型预测的剪切应力或黏度对剪切速率的双对数图、图(c)和(d)分别为剪切速率或黏度对剪切应力的双对数图。可以看到,具有屈服应力的流体特征为,在低剪切速率下应力趋向于常值(a)、观测不到牛顿区(b),而当剪切速率增加到某一临界值后,剪切应力急剧增加(a)、黏度急剧降低(b),体系开始流动;在剪切速率或黏度对剪切应力关系图中,当应力逐渐增大到某一临界值时,剪切速率急剧增加(c)、黏度急剧降低(d),体系发生宏观流动。
也需要指出,虽然上述几种模型均可以用于描述屈服应力流体的流变学行为,但在较宽剪切速率范围内,还没有一个模型能对流体整个流动行为的实验数据进行准确描述(图5)。其主要原因是,大部分屈服应力流体具有触变性,存在剪切带(shear banding)、黏度分叉(viscosity bifurcation)、局部流动(local flow)等复杂流变学现象,而这些模型对于具有较为复杂内部结构的屈服应力流体,还无法很好地进行描述[22,26]。因此,在实际使用中,需注意模型适用的剪切速率范围。
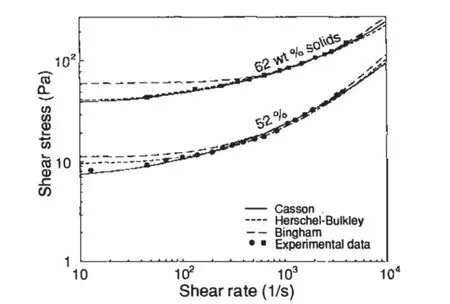
图5 三种粘弹性模型对无机颗粒悬浮液稳态剪切实验数据的拟合结果比较 [26]
2.2 屈服应力和触变性的测试方法
屈服应力的测试方法主要有三类:稳态剪切(steady shear)、瞬态剪切(transient shear)和动态剪切(dynamic shear)方法。
稳态剪切法是最经典的屈服应力测定方法[1,2,26-28]。由于简单屈服应力流体的黏度变化连续,屈服应力易于观测。简单屈服应力流体的稳态剪切流变曲线可以采用HB模型很好地描述。对于触变性屈服应力流体,通过稳态剪切测定法得到的屈服应力,与剪切速率或剪切应力扫描顺序有关。在测试中,由于黏度的变化在临界应力附近不连续,通过从低至高和相反的从高至低应力扫描所得的结果是不同的,存在触变环,屈服应力的界限并不明显[2]。从低至高扫描得到的屈服应力值,会显著大于从高至低扫描获得的屈服应力值。因此,该类方法对触变性屈服应力流体的屈服应力测试准确度并不高。此外,在稳态剪切测试中,在每个数据点,体系都需在对应剪切速率或剪切应力下平衡足够长时间以达到稳态,因而较为耗时,且仅能得到单一屈服应力这一信息,不能得到屈服应变、屈服应变速率的信息[27]。但作为最经典的测试方法,由于所得屈服应力的物理意义明确,测试也简单易行,因而仍常常被应用于屈服应力的测定。
瞬态剪切测试法包括图6所示的三种方法:阶跃剪切速率法(step shear rate)、阶跃应力(蠕变)法(step stress(creep))和应力斜坡扫描法(stress ramp)[2,28,29]。
图6(a)显示的是阶跃剪切速率法[28]。它是通过施加不同的恒定剪切速率来测定相对应的瞬时响应的应力随时间或应变的变化,将应力过冲的峰值定义为屈服应力。图6(b)所示的蠕变法,被广泛认为是屈服应力测试中最为准确的一种[2]。它是通过观测不同固定剪切应力下剪切速率的下降(剪切黏度随时间的降低)过程,将剪切应力增大到使体系发生固-液转变时的临界应力值定义为屈服应力。蠕变法需要测试前确定一个发生固-液转变的大致范围再行测试,因而与稳态剪切测试法类似,需长时间等待以判断体系是否稳定,同样耗时长。图6(c)显示的应力斜坡扫描法,则是通过测定剪切应力增大产生固-液转变的平台值而得到屈服应力[30]。该法中,不同应力扫描速率下得到的屈服平台值不同。测试时,需设定不同应力扫描速率进行测试,以消除瞬态效应影响,有时还需要非常低的扫描速率(长的扫描时间),才能得到清晰的屈服转变平台。
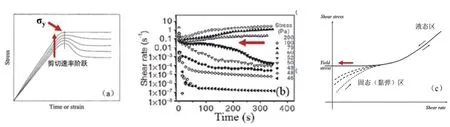
图6 瞬态剪切测试法:(a)阶跃剪切速率法; (b)阶跃应力(蠕变)法[2]; (c)应力斜坡扫描法
采用动态振荡剪切的经典确定方法有:1)通过获得的体系弹性模量G'和粘性模量G"的应力扫描曲线,将曲线中G'随应力变化偏离线性区时所对应的应力转折点(图7a),或曲线G'与G"的交点所对应的应力值(图7a),或曲线G"的最大值所对应的应力值,确定为屈服应力值[28];2)将应力-应变曲线中,应力偏离线性弹性区域的临界点(屈服点)[28](图7b),或弹性区域结束时的应力峰值,作为屈服应力值[31,32,33](图7c)。此外,还有将应力振幅和应变振幅曲线切线交点定义为屈服应力[28,34],以及对大振幅振荡剪切流场中的Lissajous曲线(应力-应变曲线和应力-应变速率曲线)采用几何平均,通过应力分叉现象来确定流体的起始屈服应力值和结束屈服应力值[35]的方法(图8)。
对流体触变性表征,通常有触变指数法、触变环法和结构破坏重建法三种方法:1)触变指数法是采用黏度计进行触变性表征的一种常用方法。它是通过测定不同高低转速下的黏度比来实现的(高低转速选定的具体值是依据不同行业和产品性能的要求而定)。该方法仅是粗略表征样品剪切变稀程度的方法,无法体现样品黏度的时间依赖行为。2)触变环法是最为常用的方法。该方法是通过对样品施加一个由低到高,然后再由高到低的剪切循环,来计算应力-剪切速率曲线封闭的面积对样品的触变性进行度量(见图1b)。3)结构破坏重建法是目前应用较多的方法。这一方法是通过对样品施加“低-高-低”三段剪切速率,从得到的黏度对时间的变化关系,来定量表征触变性(图9)。该方法既能定量比较样品剪切变稀的程度和体系结构被破坏的快慢,又可定量表征黏度的可恢复程度及快慢。这一测试方法的优势是施加的是恒定剪切速率,因此测试受仪器及夹具惯量的影响很小。此外,由于第二段所施加的剪切速率及持续时间可根据不同需要进行设置,则所得测试结果更能准确用于体系性能的评估。
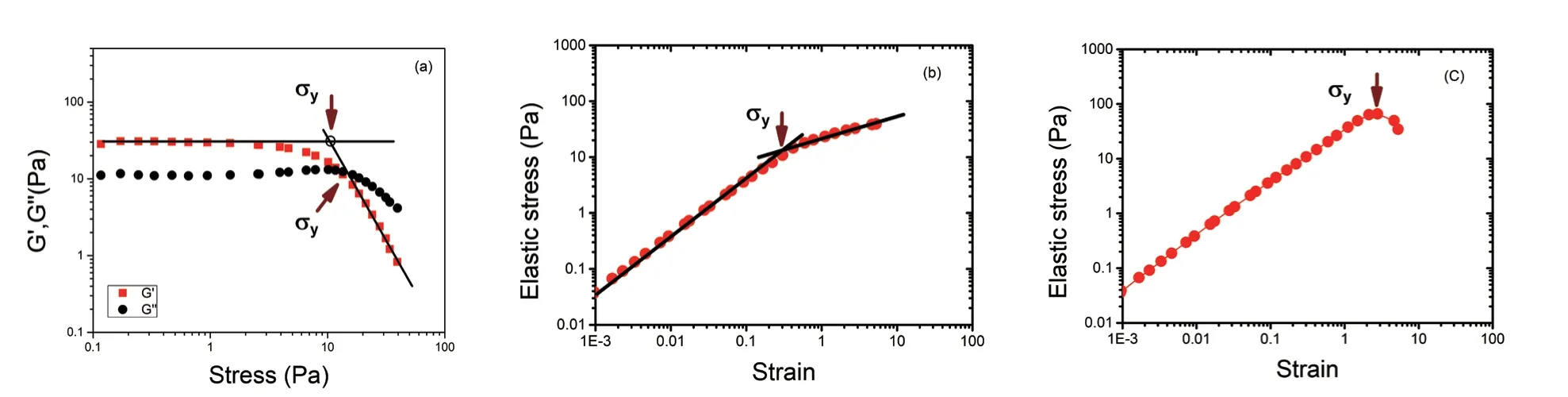
图7 动态振荡剪切法确定的屈服应力值:(a)G'偏离线性区的转折点或两模量随应力变化曲线的交点所对应的应力值;(b)应力随应变变化偏离线性弹性区时的临界点;(c)弹性应力随应变变化的峰值点
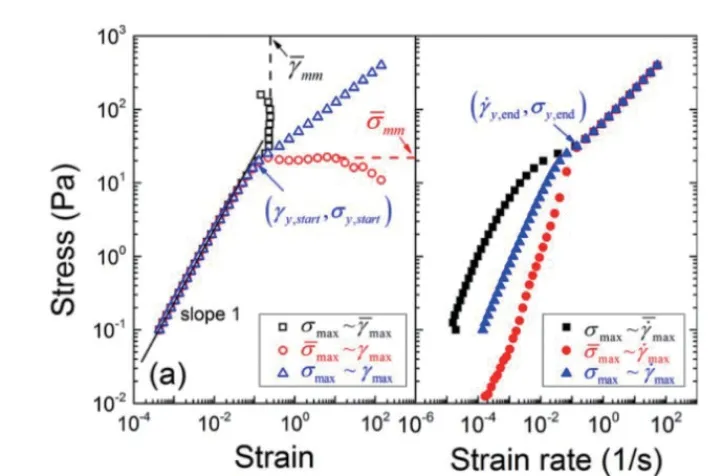
图8 大振幅振荡剪切条件下应力几何平均曲线的应力分叉现象(左图和右图分叉点分别对应起始屈服应力值和结束屈服应力值)[35]
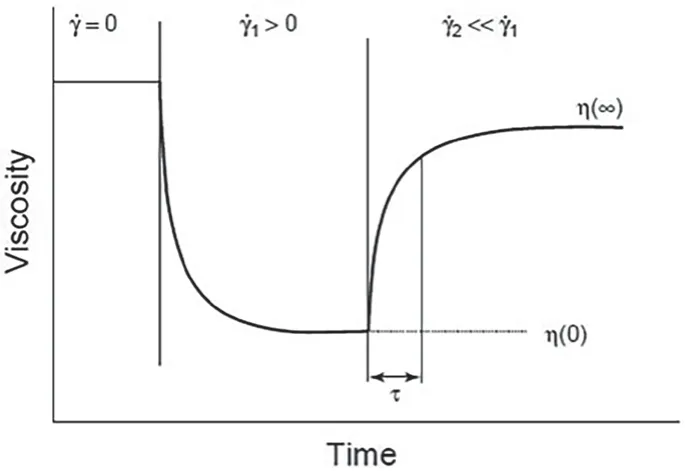
图9 触变性屈服流体在不同剪切速率下剪切黏度随时间的变化曲线
特别值得注意的是,由于触变性屈服流体的黏度同时具有两个典型特征,即剪切变稀性和时间依赖性,因此,笼统地说流体的触变性大或触变性小是不合适的,因为触变性流体不仅有剪切变稀程度的大小问题,还有黏度的时间依赖性强弱的问题。
3.屈服应力和触变性研究在墨水中的应用
墨水是典型的多相多组分复杂胶体体系,在组分上涉及性质和功能各异的着色剂(颜料、染料)、溶剂以及乳化剂、稳定剂、增稠剂、分散剂、成膜剂等多种小分子和大分子助剂,在结构上涉及从单分子形态到各类分子聚集体以及由于组分间的不相容性形成的形态各异的分散相。其中,墨水体系中分子间和不同尺度相畴间还存在着复杂的相互作用。组分的性质和组分间的相互作用决定着墨水的色光、界面附着力、出墨流畅性、抗漏性、稳定性等书写和贮存性能。这些性能从宏观的角度主要表现为墨水的流变学性质。对于一些书写墨水如中性墨水以及打印墨水,由于是触变性屈服应力流体,因此,屈服应力和触变性的准确表征对该类墨水的功能化和高性能化、配方设计和优化以及产业化生产都具有重要作用。
对中性墨水的研究表明,HB方程能很好地拟合墨水剪切应力随剪切速率的变化,具有优良书写性能的中性墨水应具有适当的黏度、较大的屈服应力、良好的触变性和假塑性等流变学性能[36]。中性墨水触变环与屈服应力值共同决定了笔芯的静态积滴墨性能。当触变环与屈服应力都较大时,会出现积滴墨现象;触变性恢复率的大小对笔芯划线时的线迹质量有显著影响;当触变性恢复率较大时,线迹容易出现中空,而触变性恢复率较小时,线迹容易出现积墨[37]。
通过对比分析黄原胶(xanthan gum)和缔合型丙烯酸酯增稠触变剂对中性墨水触变环面积以及屈服应力对屈服黏度的影响发现,黄原胶增稠效果明显,使体系具有相对较大的屈服应力与屈服黏度;而缔合型丙烯酸酯乳液受体系离子浓度影响较大,增稠后的体系具有相对较小的屈服应力和较大的屈服黏度,不当的流变学性质会造成书写时出墨量大、易漏墨现象[38,39]。增稠剂的添加量对中性墨水流变参数的影响需综合考虑,过多的添加量会导致墨水絮凝[40]。
树脂分散剂种类、炭黑的添加量及粒径分布对中性墨水的流变参数和书写性能均有影响,而后两者之间更有密切关系。树脂分散剂分子量高、炭黑添加量大、色浆中大粒径颗粒占比降低均使所配制的中性墨水的触变环面积、屈服应力和表观黏度增加,墨水的屈服值需满足一定的范围才能使墨水具有良好的书写性能[41,42]。
需要指出的是,在墨水触变性的表征中,采用低剪切速率下与高剪切速率下黏度的比值,即所谓触变指数来表征墨水触变性的方法,是有很大局限性的。高低剪切速率下黏度的比值大小,无疑在一定程度上能反映墨水剪切变稀的性质,但对任何剪切变稀流体都可得到该值,剪切变稀性质并不是触变性流体所独有。特别是,这一比值完全不能反映墨水黏度的可恢复性,以及黏度的时间依赖性的强弱。因此,尽管该法在工业应用上有简便之处,在有大量经验积累的情况下,也能在一定程度上粗略评判样品的触变性,但该法本质上主要提供的是墨水剪切变稀程度的大致信息。较全面的触变性定量表征应采用结构破坏重建法为妥。
不仅对于书写墨水,对于近些年来引起学术界和工业界广泛关注的3D打印水凝胶油墨,特别是剪切变稀的生物水凝胶油墨,其屈服应力也是一个至关重要的流变学参数。如研究发现,屈服应力是决定结冷胶(gellan gum)/明胶(gelatin)/甲基丙烯酸酯共混凝胶形成的生物油墨水凝胶生物相容性的重要指标之一[43]。高屈服强度能保证将甲基丙烯酸壳聚糖和/聚乙烯醇(PVA)混合水凝胶微粒用于细胞球状体生长仿生支架的3D打印中,具有高保真度,得到更加精细的仿生结构[44]。通过屈服应力流体体系的调控,还可以调节工业应用时对屈服应力的实际要求。如在明胶-甲基丙烯酰胺凝胶体系中添加结冷胶和调整盐浓度,可以优化凝胶的假塑性和屈服应力等流变性能[45];将水溶性甲基丙烯酸甲酯单体加入到二甲基丙烯酸酯水凝胶中,通过调控材料粘弹性可以调节3D打印的印染性能和机械性能,材料的静态屈服应力与打印所需的最佳挤压应力和打印速率有关[46];对于采用悬浮水凝胶的形式可逆包埋制造的不同尺度人体心脏成分的3D打印生物胶原蛋白,可通过调节其颗粒大小来调控体系的凝胶储能模量和屈服应力的大小[47]。
4.屈服应力研究中的挑战性问题
如何科学定义和准确测定屈服应力一直是屈服应力流体流变学研究的重点,在流变学理论和测试技术上也是一个挑战性问题[47],甚至对于是否存在真实屈服应力流体学术界也颇有争议[2]。屈服应力的测定首先需要区别流体属于简单屈服应力流体还是触变性屈服应力流体。简单屈服应力流体的流变行为与其剪切历史和热历史无必然联系,但对于触变性屈服应力流体,其流变行为强烈依赖于其剪切历史。因此,考虑已有剪切历史对屈服应力的影响是触变性屈服应力流体最重要的研究内容[48]。
目前虽然已有不少屈服应力测定方法,然而无论是依据经典的Bingham、HB 和Casson 模型的稳态剪切方法,还是后来发展而出的瞬态剪切和动态剪切方法均有其局限性。
稳态剪切方法耗时长,仅能准确描述简单屈服应力流体。瞬态剪切测试法在实施上也存在各种问题,如阶跃剪切速率或剪切应力可能没有应力过冲、蠕变耗时长、应力斜坡扫描固-液转变平台可能不明显[30]。
几类动态振荡剪切方法也有一些局限性。例如,在采用G'与G"对应力变化曲线的交点来确定屈服应力的方法中,体系在G'与G"相交之时已经发生屈服,因而所得到的屈服应力值较实际值大。并且,这种在非线性区测得的交点模量,一方面并不具备线性区模量的物理意义,另一方面,尽管交点后的G"大于G',但据此简单认为体系发生流动并无科学性。因此,这样得到的屈服应力值缺乏明确的物理意义[49]。另外,通过线性粘弹区结束时G"峰值对应的应力确定的方式,有时不能实施,因为有些屈服应力流体可能不存在G"峰值。而通过应力随应变曲线变化中应力偏离线性区起始点确定的屈服应力值与应变振幅范围有关,这种方法只能表征线性粘弹区的屈服临界点[28]。
由于屈服过程是一个松弛过程,不同条件下的测试时间尺度不同,不同测试时间尺度意味着屈服程度不同,不同测试方法对同一流体所得屈服应力值差别较大,甚至同一测试条件下对同一流体所得的结果也有可能大不相同[50],因此,屈服应力的测量值大小强烈依赖于测试条件,包括测试方法、设备、条件等[6,48,27]。此外,大量研究者对于屈服应力流体多是总体性描述,研究对象也仅基于简单屈服应力流体和触变性屈服应力流体这两种分类来进行。对很多复杂的现象(如剪切带[51]、雪崩流(avalanche flow)[52])及规律(如黏度分叉[30])无法进行归纳总结,很难得到多种条件下的普适性模型。因此,如何基于现象发展出更加准确的屈服应力流体的普适性理论模型,对各种现象及规律进行归纳性解释,也是屈服应力理论研究面临的重要挑战[14,30]。
近年来,通过各种剪切诱导流体结构破坏或数值模拟等方式对于一些典型屈服应力流体的复杂流变行为进行定性解释的研究,已有部分成效[48,28,49],然而,为系统地理解这些行为的发生原因,还需要大量的总结性工作。针对不同的屈服应力流体的特征现象进行归纳,从现象出发进行屈服过程参数的定义与测试,为屈服应力研究提供了一种新的视角,或将成为突破屈服应力研究瓶颈的重要手段之一。

