由“基本问题”出发的拓展型数学专题课探究*——以正方形中的“十字垂直”模型为例

广州市增城区教师发展中心(511300) 陈桂玲

1 问题的提出

认真研究中考试题,不难发现,试题大部分题目可以在教材找到原型,这些题根据教材上的定理、例题、习题或数学活动等进行改编. 依标务本夯实基础,试题考查中注重通性通法,淡化特殊技巧,强调对知识的深入理解和综合应用,强调考查数学思想方法,强调数学思维方式和学习能力.《义务教育数学课程标准(2022 年版)》明确提出: 要强化对数学本质的理解,通过合适的主题整合教学内容,帮助学生形成科学的思维习惯,发展核心素养[1].因此,在教学过程中,教师要重视教材,活用教材,精心设计题目,采取灵活多样的呈现方式,突出重点、突破难点. 拓展型的数学专题课能有效地引导学生进行探究,提高学生的解题能力,落实学生的数学学科核心素养. 拓展型的数学专题课,能对某一类型的题目进行研究,以问题串的梯次设计变式来呈现教学内容,以螺旋式上升的教学设计能使学生发现问题核心,提炼共性规律,理解数学本质.

但是, 仍有一部分教师忽视拓展型数学专题课的作用,认为本校的生源差,不适合开展拓展型数学专题课,能完成好新授课的内容就满足了. 这样的教师,培养出来的学生的思维得不到发散, 解题能力平庸; 也有一部分教师有开展拓展型数学专题课, 但是收效甚微. 究其原因, 发现他们开展专题课的模式单一: 精选1 至2 道例题——教师讲评示范——学生训练——师生总结;或者,学生课前过关训练——教师讲评——师生总结. 这样的专题课模型存在的问题是例题题目量多但是不精,知识点反复出现,学生重复训练,难以掌握思索背后的规律. 上好拓展型数学专题课,就要引导学生分析问题的本质特征,寻找某些不同问题之间的共性,启发学生的模型意识,辨析模型使用的条件,归纳解题策略,迁移知识,渗透数学思想,提升学生的关键能力.

2 由“基本问题”出发的拓展型数学专题课实践探索

在目前的教学中,我们常见的专题拓展课主要基于以下两种类型: (1)基于“数学思想方法”共存共通的专题课; (2)基于“经典模型”广泛适用性的拓展专题课. 以上两种类型的专题课都是基于某种“基本图形”进行拓展延伸而来的,而笔者想跟大家分享的是实用型拓展数学专题课——由“基本问题”出发的拓展型数学专题课. 下面以“以正方形中的‘十字垂直’”模型为例,对由“基本问题”出发的拓展型数学专题课进行实践探索.

2.1 引入典型例题,提炼基本问题

基本问题是指能对核心内容的引起探究,从而激起深度思考,内化学生的学习经验,进一步迁移知识[2]. 典型例题可以是教材里的例题或习题, 也可以是中考题的原题或改编题, 例1就是改编人教版数学八年级下册第68页的第8 题.

例1如图1,在正方形ABCD中,点E、F分别在BC、CD上,且AE⊥BF,求证:AE=BF.

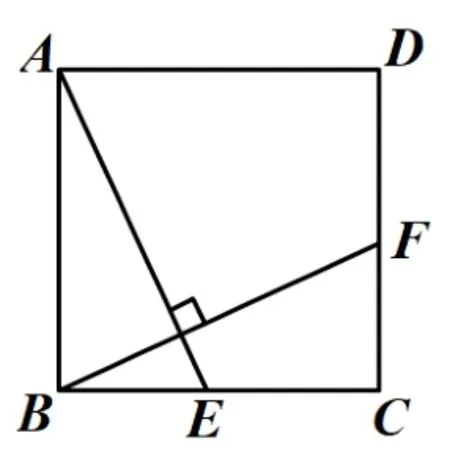
图1

分析: 根据题目条件中的垂直关系, 由“ASA”可证ΔABEΔBCF,由全等的性质: 两个三角形全等的对应边相等,可得AE=BF.

设计意图: 由学生熟悉的三角形全等入手,提炼基本问题: 由正方形中两线段互相垂直的位置关系如何推出数量关系? 引出正方形中的“十字垂直”模型. 本例题能改变线段的位置或把题目中的正方形变为矩形,能进一步拓展延伸,引发学生深入探究.

2.2 逐步变式拓展,凸显数学本质

通过对例题进行不断地变式, 如改变条件或改变图形,引导学生逐步领悟,层层深入到核心内容,促进学生理解数学本质,提升数学思维.

变式1: 如图2,在正方形ABCD中,已知点E、F、G、H分别在AB、CD、BC、AD上任意一点,EF⊥GH,探究EF与GH的数量关系,并证明你的结论.

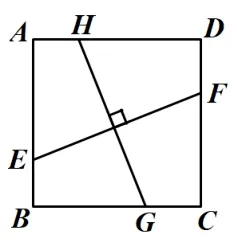
图2

分析: 依据例1 的解题方法启示, 构造两条线段所在的三角形全等. 解法一, 作垂直, 如图3, 由“ASA”可证ΔEPFΔHQG, 可得EF=GH; 解法二, 作平行(平移) , 如图4, 由“ASA”可证ΔBCPΔABQ, 可得BP=AQ,证得EF=GH.

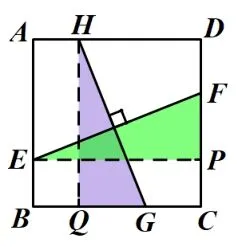
图3

图4

设计意图: 通过变式,探究出正方形中相交的两条垂线段问题的辅助线作法与核心解题方法,层层引导,让学生感受类比、转化、数形结合等数学思想.

变式2: 如图5,将边长为4 的正方形纸片ABCD折叠,使得点A落在CD的中点E处,折痕为FG,点F在AD边上,点G在BC边上,求折痕FG的长.

图5

分析: 由题目中的折叠条件,求拆痕FG,想到连接AE,利用对称的性质,得到AE⊥FG,依据变式1 的解题方法启示,构造两条线段所在的三角形全等,如图6,由“ASA”可证ΔADEΔGHF,证得.

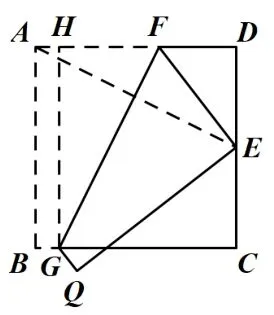
图6

设计意图: 由基本问题中的正方形十字模型图形,变式为只有一条线段,教师可以引导学生自主探究、动手操作、分析问题,从而培养学生在正方形图形中的十字垂直模型的意识,渗透转化的数学思想.

变式3:如图7,在矩形ABCD中,AB=m,AD=n,点G,H,F,E分别在AB,BC,CD,AD上任意一点,EH⊥GF,探究EH与GF的数量关系,并证明你的结论.

图7

分析: 由正方形的四条边相等, 通过证两个三角形全等得到两条垂直线段相等, 而矩形的两条邻边成比例, 依据变式1 和变式3 的解题方法启示, 构造两个三角形相似,具体方法是: 作垂直, 如图8, 可证ΔEHK∽ΔGFP, 可得; 或可作平行(平移) , 得到GF=BP,EH=CK,如图9,可证ΔCDK∽ΔBCP,可得.

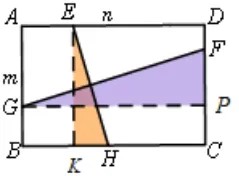
图8

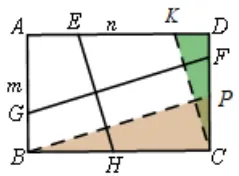
图9

设计意图: 由基本图形中,由正方形拓展到矩形,对教学内容进行结构化,逐步突显数学本质的理解,培养学生类比思想,迁移知识的能力.

变式4: 如图10,在四边形ABCD中,若AB=AD=10,BC=CD= 5,∠ABC= 90°,AM⊥DN,点M、N分别在BC、AB上,求的值.

图10

分析: 根据题目的条件,由AM⊥DN,可联想到构造十字垂直模型,由变式3 的解题方法启示,求AD MN的值,可转化为求B AB P的值,连接AC,构造矩形ABPQ,如图11,易证ΔADCΔABC,得到∠B= ∠ADC= 90°,由“AA”易证ΔPCD∽ΔQDA,得到,设PD=x,则AQ=2x,DQ=10-x,在RtΔAQD中,利用勾股定理,可得AQ=8,即BP=8,求得.

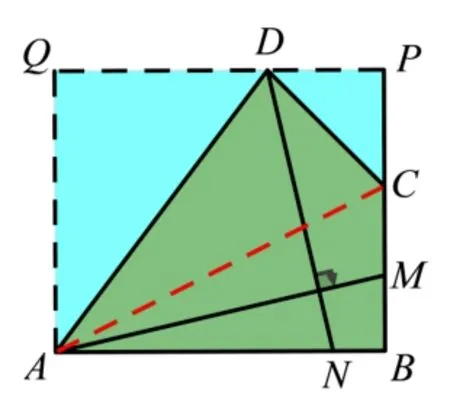
图11

设计意图: 本题难度较大,从基本图形和条件都进行了变换,目的是培养学生辨析十字模型使用的条件,灵活运用十字模型,突显解题的数学思维本质.

2.3 归纳共性规律,形成解题策略

在变式拓展延伸过程中,引导学生建立知识的内在交叉联系,让学生发现在“变”的现象中,提取“不变”的数学本质,从“不变”的数学本质中,探索“变”的规律,发散学生的思维,最后提炼出通性通法,从而提高学生的解题能力,发展学生的数学核心素养. 如在“十字模型”,可以归纳如下:

如图12,正方形的“十字模型”.

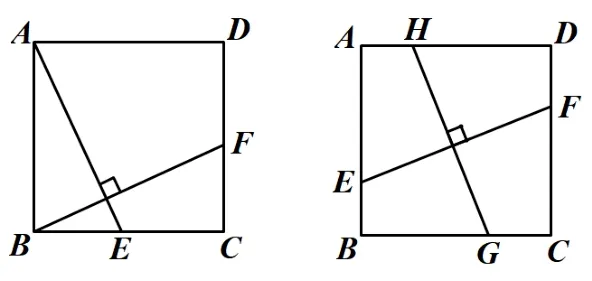
图12

图形特征: 端点在对边上,互相垂直.

基本结论: 垂直线段相等.

解题策略: 利用或构造三角形全等.

如图13,矩形的“十字模型”.

图13

图形特征: 端点在对边上,互相垂直.

基本结论: 垂直线段之比等于矩形邻边比.

解题策略: 利用或构造三角形相似.

2.4 综合训练反馈,建立横向网络

由基本问题出发,综合多种知识的灵活运用,引导学生建立知识的横向网络[3]. 渗透数学思想,锻炼解题能力,促进几何直观、推理能力与抽象能力等数学核心素养达成,发展高阶思维品质.”

例2如图14, 在正方形ABCD中, 点E是边AB上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交于AD点F.

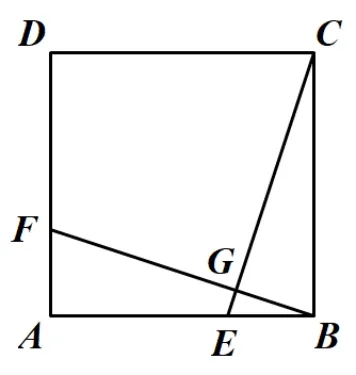
图14

(1)求证:BF=CE;

(2)若AB= 4,连接AG,如图15,当点E在边AB上运动的过程中,AG是否存在最小值,若存在,请求出AG的最小值,若不存在,请说明理由.

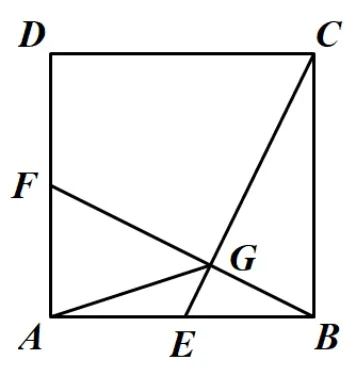
图15

分析: 第(1)问,由“ASA”可证ΔABFΔBCE;第(2)问,由BF⊥CE,正方形的边长为4,易得∠BGC= 90°,BC= 4,可知点G在以BC为直径的⊙O一段弧上运动,连接AO,OG,如图16,当点A,G,O三点共线时,AG有最小值,由勾股定理可求的长,再求得.

设计意图: 综合运用正方形的性质,全等三角形的判定和性质,定弦定角的隐圆模型求线段的最小值,体会解决动态问题时需要“动着想、定着做”的数学思维,领悟数形结合、转化等数学思想方法的妙招.

图16

3 结束语

为了让课堂效率最大化,可以把典型例题和难度较大的变式题分解成动手操作题,然后设计为前置作业,不占用课堂时间,让学生提前做. 如变式2 中,设计动手操作题: 如图17,请剪出的边长为4cm的正方形纸片,然后折叠,使得点A落在CD的中点E处,折痕为FG,点F在AD边上,点G在BC边上,画出折痕FG的长,你能求出折痕FG的长吗?通过前置作业,一方面,能培养学生的自主合作探究的学习能力,另一方面,让学生提前回顾知识,也留下悬念,带着问题进行课堂探究,推动课堂的高质量发展.

图17