一道填空题的改编命制历程与反思

东莞市第十高级中学(523981) 许浩杰

随着高中数学新课程标准的落实,有利于发展学生数学核心素养的新题型得到了开发与使用. 近年,从高考题到各省市的高考模拟题,大家都在探索研究不同试题类型的命制方式. 在改编一道填空题中,经历了从封闭性问题到开放性问题的调整,在此谈谈对两类题目命制的体会和反思.

1 关于封闭性问题与开放性问题

高考数学具体试题类型一般包括封闭性问题与开放性问题两类试题类型.

在我国的数学教学与评估中使用的问题主要是计算题、论证题、常规题的应用题和填充题,这些问题的答案只有正确与不正确(包括不完整)两种,并且正确的答案是惟一的.这些问题给出的条件往往都是用得着的,而且只用一次. 这一类问题叫封闭性问题(closed problem),它是我国数学教学的基础. 此类试题能体现“回课本、重概念、考通法”,体现数学试题的普适性. 试题解题方法注重通性通法,贴近日常教学,突出能力和素养的考查.

开放性问题(open-ended question),又称构造性反应. 它要求被试创造一个反应,而封闭性问题则要求被试回忆、选择一个反应. 开放性问题的特点是结论、条件、思路都是开放的. 而结构不良题就属于开放性问题,是指试题开放设问,问题的条件、数据等部分缺失或冗余,问题目标界定不明确,要求学生综合运用所学知识进行探究. 结构不良题类型包括条件开放、结论开放、条件结论均开放等.

2019 年教育部考试中心发布的中国高考评价体系中指出,高考重点考查学科的核心素养,进一步关注学生的知识应用、数学探索等方面的能力. 结构不良题给学生提供了开放的探究空间,能很好地培养学生的思维创造力.

2 题目命制历程

2.1 试题原题与解析

试题原题如图1, 在棱长为3 的正方体ABCD-A1B1C1D1中,点N在该正方体的棱上运动,则有____个满足条件的点N,使得点N到平面A1BC1的距离为.

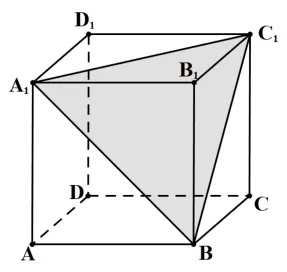
图1

解析: 在正方体ABCD-A1B1C1D1中, 当点N运动到与点B1重合时, 三棱锥B1-A1BC1的体积为:(h为点B1到平面A1BC1的距离),而等边三角形ΔA1BC1的面积为:

由等体积法得:

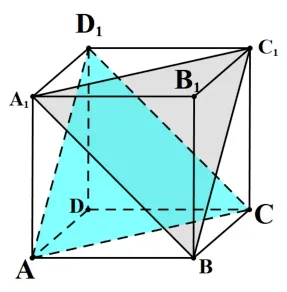
图2

综上所述, 有4 个满足条件的点N, 使得N到平面A1BC1的距离为.

在解决上面这道题目时,发现随着点到直线的距离的变化,满足条件的点的数量也将随之变化. 这个发现让笔者解后久久回味,在脑袋里酝酿着如何改编该题.

2.2 改编版本1: 常规题

第一个想法是将原题改编成常规题,包括两个问,形成难易梯度,其中第一个问相对容易,占2 分,第二个问难度较大,需要学生画图、计算、分情况探究等,占3 分. 改编的思路是第一问求正方体一个特定的顶点到指定平面的距离,第二个问打破原题的那几个顶点的特殊性,引导学生去探求满足条件的点的数量.

改编题1在正方体ABCD-A1B1C1D1中,棱长为1,点P在该正方体的棱上运动,则当点P运动到与点B1重合时,点P到平面A1BC1的距离为____; 另外,当点P到平面A1BC1的距离为时,有____个满足条件的点P.

解析: (1) 在正方体ABCD-A1B1C1D1中, 当点P运动到与点B1重合时,三棱锥B1-A1BC1的体积为:(h为点B1到平面A1BC1的距离),而

由等体积法得:

(2)由(1)知点B1到平面A1BC1的距离为,连接AD1,AC,CD1,有平面A1BC1与平面AD1C平行,同理可计算出点A,D1,C到平面A1BC1的距离也为.当点P运动到与点D重合时,

同理可得点D到平面A1BC1的距离为. 这是正方体棱上动点P到平面A1BC1的最大距离.

根据点到平面距离的变化,可以分成以下4类情况:

1)当点P到平面A1BC1的距离为时,有4个满足条件的点P.

2)当点P到平面A1BC1的距离在范围中时,可在平面A1BC1与平面AD1C之间作平行平面α, 可知平面α与正方形的棱有6 个交点; 同理, 在点B1与平面A1BC1之间作平面β与平面A1BC1平行,可知平面β与正方形的棱有3 个交点. 故有9 个满足条件的点P,如图3 所示.

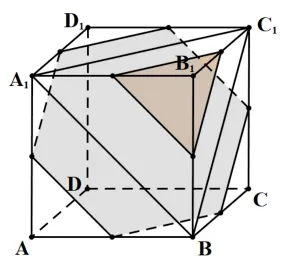
图3

3)当点P到平面A1BC1的距离在范围中时,同理有3 个满足条件的点P,如图4 所示.

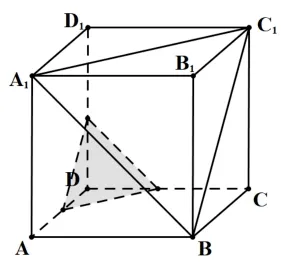
图4

4) 当点P到平面A1BC1的距离为时, 有1 个满足条件的点P. 故当点P到平面A1BC1的距离为时, 属于第二类情况, 故有9 个满足条件的点P.

这个常规题的改编版本由原题的一问调整为两问. 考查学生立体几何的综合应用,综合考查线面垂直与面面平行的判定与性质等知识点,训练学生画简图、灵活使用等体积法求点到平面距离、利用平面动态平移等技巧,考查学生转化与化归等思想方法,综合考查学生分析、解决问题等能力.

两个问的设定,使题目有了梯度性,从特殊性走向拓展,可进一步延伸到题目的其他情况;第二小问设置数值,引导学生探究题目的不同情况,并最终得到时,属于第二类情况,锻炼了其逻辑推理能力.

2.3 改编版本2: 结构不良题

经过第一版常规题的改编,笔者觉得还不能很好地通过题目引导学生去探索发现. 题目的要求相对直接,学生被动式地完成题目,没能更好地发挥题目隐藏的学生可多情况破题的作用. 从而有了下面第二版本的改编题.

改编题2在正方体ABCD-A1B1C1D1中,棱长为1,点P在该正方体的棱上运动,则当点P运动到与点B1重合时,点P到平面A1BC1的距离为____; 另外,当点P到平面A1BC1的距离为____(可填具体数值或区间范围)时,有____个满足条件的点P.

第二版本的题目主要在于第二小问调整为结构不良题,让学生随着题目的探究,锻炼了其逻辑推理能力,可呈现学生不同的思考成果,也让答案有了更多的可能性.

题目编好之后, 考虑到题目3 个空共5 分, 第一个问2分,第二问结构不良占3 分,分值和考试时学生完成此题所用的时间量相关性太弱,且第一问所求的距离求出来后可以直接套入第二问的解答中,从而失去了命制本来计划达到的解答多样性的效果. 此版本改编题目还得改.

为了让题目更好地引导学生探究,同时简化题目三个空的设置,第三版的题目删掉了第一个问,保留了后面的问题.

改编题3在正方体ABCD-A1B1C1D1中,棱长为1,点P在该正方体的棱上运动,当点P到平面A1BC1的距离为____(可填具体数值或区间范围)时,有____个满足条件的点P.

此版改编题,虽然出现了多种解答结果,但是学生画图可敏感发现P到平面A1BC1的距离最大的点为点P与点D重合时,且只有1 个满足条件的点. 题目有了这个特殊情况,导致学生都奔着点D去解题,没能达到结构不良题所起的作用,得继续调整修改.

为此,笔者查阅并学习了近年高考题中结构不良题的命制形式,通过设置3 个不同距离数值,改编成第四版题目.

改编题4在正方体ABCD-A1B1C1D1中,棱长为1,点P在该正方体的棱上运动,在①当点P到平面A1BC1的距离为, ②当点P到平面A1BC1的距离为,③当点P到平面A1BC1的距离为这三个条件中任选一个,补充在下面问题中,并给出相应结论.

在正方体ABCD-A1B1C1D1中,棱长为1,点P在该正方体的棱上运动,____(三选一,填序号①或②或③)时,有____个满足条件的点P.

最后版本的改编题,通过不同条件的设定,使题目情况多样化,给学生的探究带来不同的指引,从原题的特殊性研究走向多方向探究,引导学生进一步拓展到所有情况. 考虑到题目每个条件的难度和题目的科学性,没有把全部情况放开让学生自由选择,只提供了3 个不同的数值作为解题条件.

至此,改编的题目虽还有瑕疵,但也大致展现了结构不良题的优势,给学生解题提供了多种可能性.

3 几点思考

通过以上题目的改编历程,从常规题到结构不良题,可以发现:

首先,题目命制要注意梯度性. 通过第一版本常规题的改编,题目从一个问调整为两个问,形成难度差异,使题目有了梯度,有利于学生由易到难层层递进解决问题.

其次,题目命制要注意指向性. 在编制第二版本结构不良题时,设置的3 个空使得题目冗长且第一个问影响到后续解题的方向,通过改编,笔者及时对题目进行调整,命制时考虑问题指向清晰,避免学生思维受限制,防止题目出现设计之外的思维漏洞.

特别的,题目命制要注意科学性. 在命制结构不良题时,作为命题者,题目结论的每种可能性都要提前研究透彻,避免出现难度差异过大的情况,最好能使每个解决方案在任务耗时、操作难度、思维水平等方面都相对持平.

总之,在题目命制的过程中,命题者应落实以德树人的宗旨,基于高中数学新课程标准的理念,以培养学生数学核心素养为指导,充分发挥题目对提升学生数学核心素养的积极作用.