对“新教材”中“正态分布”概念引入的“频率分布直方图”的修改建议

广东省佛山市顺德区 勒流中学(528322) 邓先春 李翠平

人民教育出版社(2020 年3 月第1 版)普通高中数学教科书(以下简称“新教材”)选择性必修第三册教科书7.5 正态分布一节内容,对连续型随机变量服从的一个常用的概率分布的编写采用了与“旧教材”不同的处理方式来引入“正态分布”的概念,二者引入的方式各有千秋,此文不作详解. 本文着重对“新教材”通过实例数据处理中引用频率分布直方图表达有不同的理解,并给出相应的修改意见与同行商榷.

“新教材”必修第二册P192～197“总体取值规律的估计”一节内容中对“频率分布直方图”学习进行编写,与画频数分布直方图类似,可以按: ①求极差, ②决定组距与组数, ③将数据分组, ④列频率分布表, ⑤画频率分布直方图等五个步骤完成“频率分布直方图”的制作. 这样我们通过频率分布直方图就可以清楚地知道数据分布在各小组的个数与频率. 这里抽样采集的数据均为非负数并用x表示. 因此图中的横轴只需要x≥0 即可,纵轴表示,纵轴也只需要y≥0 即可.

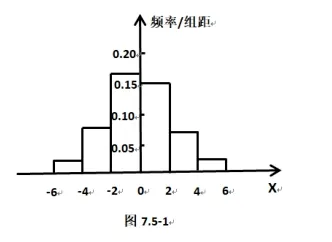
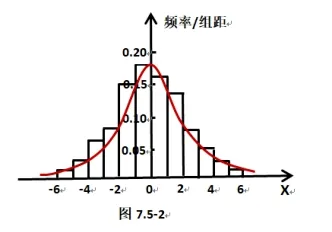
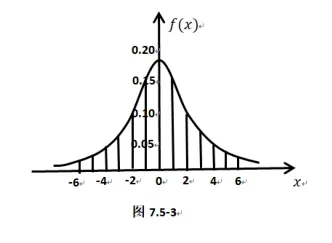
“新教材”选择性必修第三册P83～87“正态分布”一节内容中对“正态分布”学习进行编写. 而“旧教材”编写是通过“高尔顿板”的实验直观得到小球最后落入格子的号码为随机变量X所对应的频率分布直方图.“新教材”编写是通过具体实际问题, 随机抽取n= 100 的样本, 样本点其质量与标准质量之差X是一个随机变量. 由于X=实际质量-标准质量,因此X可能出现x＜0 的数据. 从样本数据中可见Xmin= -5.2 ＜0,Xmax= 4.8＞0, 极差为4.8-(-5.2) = 10, 选取组距为2, 则可以分为5 组; 由于实际问题需要,在制作随机变量X频率分布直方图时需要分成6 组: [-6,-4),[-4,-2),[-2,0),[0,2),[2,4),[4,6]; 而P83图7.5-1 与P84图7.5-2,及图7.5-3 表示此问题中随机变量X的频率分布直方图中,纵轴表示的尽管为非负数,但为了与正态密度函数图像相对应,此时把纵轴画在x= 0位置就是更为严谨妥当;这与必修第二册中的频率分布直方图中随机变量x≥0 不同的是: 此时x＜0,x=0,x＞0,这与正态密度函数的定义域为R相吻合了.

现将“新教材”中P83图7.5-1 与P84图7.5-2,图7.5-3 表示此问题中随机变量X的频率分布直方图修改为下面的图形:

以上修改仅供大家参考.