几何模型在解题应用中“走火入魔”现象的分析*

华南师范大学数学科学学院(510631) 陈碧玉 苏洪雨

1 几何模型在解题中的价值

几何模型是对平面几何问题中常见几何图形的性质,及其中所蕴含的数学规律、数学思想方法的提炼. 例如“手拉手模型”、“半角模型”等.

在考试作为基本评价模式的背景下,培养学生的解题能力十分重要. 初中阶段平面几何的问题考察对于学生来说普遍偏难. 于是教师在长期的教学实践中对平面几何的问题作进一步归纳总结,形成几何模型. 通过几何模型,揭示隐藏其中的图形对称、平移、旋转的性质,问题解决的常用方法如构造法等,让解题变得有迹可循. 几何模型也揭示了一类问题的本质,强化问题解决策略的学习,促进正向迁移的发生.

几何模型就如同棋谱中的定式, 运用几何模型解题能大大缩短思维的时间,更快地接近目标,起到化繁为简的目的[1]. 学生掌握几何模型可以丰富他们的解题经验,从更高的角度看待问题,掌握一类问题的本质. 学生在解题时只需根据模型的特征识别出模型,便可快速得到正确的解题方向,减轻思维负担,加快解题速度.

2 “走火入魔”的反例

随着平面几何教学的深入与考察难度的增加,几何模型深受命题者的青睐. 但是目前习题的质量参差不齐,命题者对几何模型的追求也开始出现“走火入魔”的现象.

题目重现如图1, ∠A= ∠B= 90°,CA=CB= 4,∠ACB= 120°,∠ECF= 60°,AE= 3,BF= 2,求五边形ACBFE的面积.

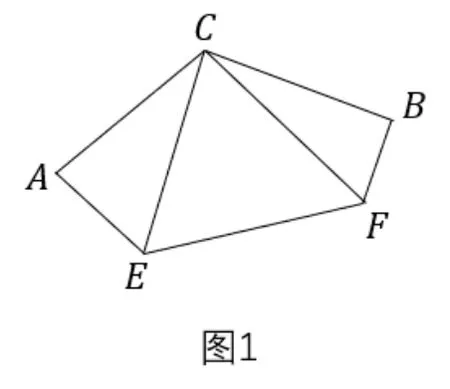
解法一(半角模型) : 延长FB至点M, 使得BM=AE= 3, 连接CM, 如图2所示. ∵CA=CB=4,∠CAE= ∠CBM= 90°, ∴ΔCAEΔCBM(SAS).∴CE=CM,∠ACE= ∠BCM. 由题∠ACB= 120°,∴∠FCM= ∠BCM+∠FCB= ∠ACB-∠ECF= 60°.又CF为公共边,∴ΔECFΔMCF(SAS). ∴SΔECF=SΔMCF=SΔCAE+SΔCBF=10,S五边形ACBEF=20.

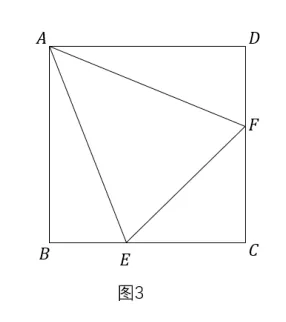
半角模型如图3, 在正方形ABCD中,E、F分别在BC、CD上,且∠EAF= 45°,连接AE、AF、EF,那么EF=BE+DF. 若E、F分别在CB、DF延长线上时,结论变为EF=DF-BE.

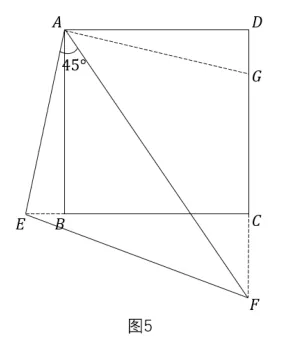
当E、F分别在BC、CD上时, 延长CD到点G, 使得BE=DG(补短) , 如图4. 易证ΔABEΔADG(SAS), 得AE=AG, ∠GAF= 45°.易证ΔAFEΔAFG(SAS),结论得证. 若E、F分别在CB、DF延长线上时,在DC上取点G,使得BE=DG(截长),如图5. 同理可证.

通过补短或者截长的形式, 构造出第一对全等三角形,这一对全等三角形可以看成由原三角形旋转形成; 同时也构造出另一个半角, 即∠GAF= ∠BAD- ∠EAF, 而∠EAF= 45°, 都为∠BAD的一半, 恰好为一对相等的角,出现第二对全等三角形.十分关键,故称为半角模型.

使用半角模型的条件是有边(AB和AD)相等,且中间分割出一个半角. 半角模型的使用方法是进行补短或者截长.

解法二(解三角形): 由勾股定理,可得CE= 5,;那么.

所以,

为何两种解法会出现不一样的结果?

3 问题的本质分析

问题源于人教版八年级上册第十二章“全等三角形”的课后作业,定位为一道初中几何问题. 考察的知识点是全等三角形,若学生只掌握全等三角形,较难求解本题. 而题目中已有两边相等以及120° 的半角,根据半角模型,采取补短边的方法,使得ΔCAE可以旋转到ΔCBM的位置上,便会出现全等三角形. 从几何模型的角度便可轻松得到解法一.

解法二则是在不考虑考察对象知识储备的限制下,运用高中阶段三角函数的知识去求解. 问题的难点是求ΔCEF的面积,运用两边乘夹角正弦值求三角形面积的方法十分容易解决. 但此时存在一个疑问: 题目的一个条件∠ACB=120° 没有用上,这个条件是否是多余的,或者是干扰项?

汇总两种解法发现得到的答案并不一致,两种解法各自也不存在错误. 仔细分析两种解法的差异,发现解法一使用了“∠ACB=120°”的条件,而解法二没有. 顺着这个思路分析发现,ΔCAE和ΔCBF已有两边及一个角是确定的,从解三角形的角度,∠ACE和∠BCF是确定的,那么∠ACB也能通过计算确定. 通过计算发现,∠ACB≈123.43°,大于120°. 而“∠ACB=120°”是呈现半角模型的重要条件,命题者为了体现半角模型添加了一个错误的条件,导致题目违背事实,才出现了结果不一致的情况.

4 几何模型应用的反思和建议

4.1 基于几何模型的学习要注重过程性

在学习几何模型的过程中,学生应在经历几何模型应用的过程中不断加深对平面几何知识的理解,提炼方法,培养模型观念. 只有在几何模型的学习中弄清知识的来龙去脉,建立知识网络,才能在综合的情境中识别出问题的本质,成功解决问题. 仅将几何模型看成解题的工具,学生容易形成思维定势,不利于数学的学习.

4.2 几何模型问题设计要科学合理,避免生搬硬套

问题出错的根本原因在于命题者为了体现半角模型添加了一个错误的条件,所谓过犹不及. 同时命题者的命题思路不自然,导致解题者的解题思路也不流畅. 很多八年级的学生对这道题一筹莫展,反而达不到训练的效果. 强扭的瓜不甜,命题者不能为了考察某个知识点或者体现难度而生搬硬套,使问题违背事实.

4.3 几何模型教学要体现数学的本质

几何模型是对一些平面几何问题的高度概括与总结. 在初中平面几何的教学中,切忌只向学生展示模型的内容与结论. 教师应在学生掌握相关基础知识之后,适时提炼总结,揭示本质,让学生理解几何模型的逻辑规则和方法,并注意避免模型思维定势. 从中帮助学生理清知识的脉络与结构,促进发生知识迁移;形成模型观念,提升解决问题的能力.