在“活动化教学”中发展学生的核心素养——以“平行四边形(第1 课时)”为例

广州市黄埔区玉岩实验学校(511363) 杨 雄

《义务教育数学课程标准(2022 版)》指出: 义务教育数学课程应使学生通过数学的学习,形成和发展面向未来社会和个人发展所需要的核心素养[1]. 学生数学核心素养的发展应当落实到每一节课中,笔者在人教版《义务教育教科书·数学》八年级下册第十八章“平行四边形(第1 课时)”教学中,采用“活动化教学”方式,发展学生的数学核心素养.

活动化教学是以数学活动为载体,将教学内容巧妙地融合在活动中,学生在“画一画”、“拼一拼”、“转一转”、“变一变”、以及“观察、测量、实验、猜想、证明”等一系列活动中发现数学问题,并揭示数学规律及本质[2]. 活动化教学的意义在于借助活动这个载体, 让学生在亲自动手实践的过程中,更加深刻体会知识的内涵与外延. 它在培育学生的符号意识、几何直观、推理能力、空间观念、模型思想、应用意识和创新意识等核心素养显得尤为重要, 现将“平行四边形”(第1课时)课堂教学的关键环节摘录出来,与读者共研.

1 善用情境 引领学生数学思维自然生长——画一画

1.1 情境引入,回顾三角形的学习历程

问题1: 老师在学案上画出了一个一般的三角形,请你再画出两个特殊的三角形.

提问1: 你画出了一个什么特殊三角形?

学生A:等腰三角形.

提问2: 由一般三角形到等腰三角形需要具备什么条件?

学生A:增加两条边相等.

提问3: 还可以得到其他的特殊的三角形吗?

学生B:等边三角形.

提问4: 等边三角形是将等腰三角形的边进一步特殊化,除了将边特殊化,你还可以将什么特殊化?

学生B:将角特殊化,一个角等于90°,得到直角三角形.

提问5: 在等腰三角形和直角三角形的基础上各自增加一个条件,变成更为特殊的三角形,请问这个三角形是什么三角形?

学生: 等腰直角三角形.

提问6: 由等腰三角形到等腰直角三角形需要增加什么条件? 由直角三角形到等腰直角三角形又需要增加什么条件?

师生讨论,共同完成板书(如图1)

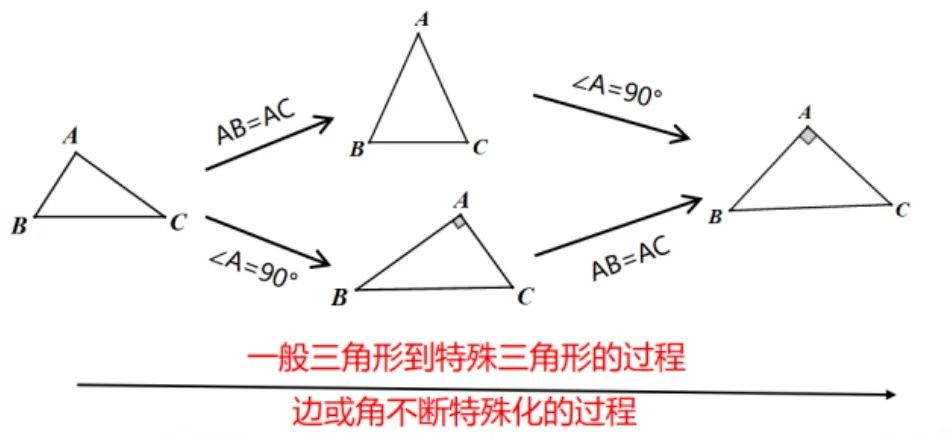
图1

提问6: 我们是如何研究等腰三角形的? 或者说研究等腰三角形的一般思路是什么?

学生C:定义、性质、判定.

提问7: 等腰三角形有什么性质?

学生D:两腰相等;两底角相等;“三线合一”.

1.2 类比思考,建构平行四边形内容框架

问题2: 你觉得我们如何学习平行四边形? 请在学案上写(画)你的想法.

提问1: 学完三角形之后,我们学习了四边形,什么叫四边形的对边? 什么叫四边形的对角?

学生: 不相邻的两条边称为对边,无公共边的两个角称为对角.

提问2: 当四边形的两组对边互相平行时,四边形就变成了平行四边形. 我们学过那些特殊的平行四边形?

学生C:长方形

提问3: 平行四边形变成长方形,需要具备什么条件?

学生C:将角特殊化,让一个角等于90°.

……

学生在老师的引导下形成如图2 所示的学习内容的结构图.

图2

数学教学价值的实现,学生数学素养的发展,依赖于教学内容的选择和教学时序的安排,特别是教学情境的选择和使用. 本节课选择等腰三角形的学习历程这一数学现实作为教学情境,是因为平行四边形和等腰三角形以及他们的特例都是用“属+种差”的方式定义的,这就决定了研究的数学思维方式具有一致性,等腰三角形的学习历程回顾有利于学生的数学思维自然的、高质量地生长[3].

2 巧设探究 引导学生多角度“猜想”——拼一拼

本节课的教学重点是平行四边形性质的探究与证明,如何引导学生发现结论、形成猜想,显得尤为关键和重要,为了不束缚学生的思维,我准备了一套学具: 一对纸质全等的三角形和一个纸质的平行四边形. 在学习完平行四边形的定义和表示方法之后,我抛出了如下问题: 平行四边形除了“两组对边分别平行”外,它的边之间还有什么关系? 它的角之间有什么关系?

2.1 拼一拼全等三角形

提问1: 你认为平行四边形的边和角还有什么关系?

学生A:平行四边形的对边相等,对角相等.

提问2: 你是怎么得到这个结论的?

学生A:(边说边演示)我利用手中的全等三角形(如图3),可以拼成一个平行四边形(如图4),全等三角形的对应边变成的平行四边形的对边,当然相等;平行四边形的一组对角是全等三角形的一组对应角,另外一组对角则是全等三角形两外两组对应角的和.

图3 图4

2.2 量一量平行四边形

提问3: 前面的同学用拼的方法对平行四边形的边和角进行了猜想,你还有别的办法吗?

学生B:可以用量的方法,用刻度尺去量平行四边形的边,用量角器去量平行四边形的角.

老师: 不错,这种方法我们在小组也采用过,现在老师借助几何画板再次验证.

2.3 转一转平行四边形

提问4: 有个同学进行了如下操作,他说也能够得到平行四边形对边相等,对角相等的结论,你看看是否有道理. 首先,他在黑板上画了一个平行四边形;接着,剪一个和黑板上的一模一样的纸质平行四边形;然后,他画出了纸质平行四边形对角线的交点;

图5

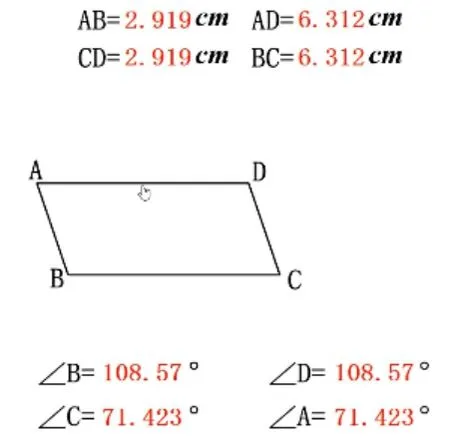
图6

最后,让纸质的平行四边形与和黑板上的平行四边形重合,按住交点,将平行四边形转动180°,发现转动之后的平行四边形仍然与黑板上的平行四边形重合.

他说这样也能够得到平行四边形对边相等, 对角相等,你认为他对吗? 为什么这样也可以得到结论呢?

学生C:旋转180°之后,上面的边到了下面,左边的边到了右边,仍然重合,说明对边相等;旋转180° 之后,对角也刚好互换,仍然重合,说明对角相等.

老师在抛出了问题之后,没有多做引导,而是让学生独立的、开放的通过直观观察和动手操作发现性质,这样的处理方式为学生的深层次思考留足了时间; 开放探究的方式,既为学生丰富多彩的探究路径创造了空间,也给学生呈现了问题解决方法的多样性;给学生带来了不同的学习体验的同时,也让不同的学生在数学上得到不同的发展.

3 精讲例题 引发学生的多样化思考——变一变

几何内容的核心价值是发展学生的数学抽象、直观想象和逻辑推理能力. 几何变换对直观想象能力的发展、几何推理对逻辑推理能力的发展分别具有举足轻重的作用[4]. 因此,在几何教学实践中,应精讲例题,教会学生用分析法思考,用综合法书写,落实逻辑推理能力的培养;也应精编配套习题,在例题与习题中渗透几何变换的思想,让学生领悟到变的是条件和图形,不变的图形的性质.

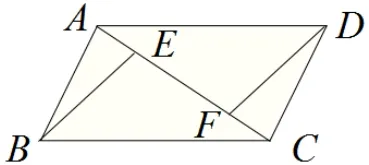
图7

图8

追问1: 除了证明ΔABEΔCDF之外,还有其他的证明方法吗?

追问2: 如何理解BE与DF的关系?

追问3: 例题和习题都是由“AE=CF”来推到“BE=DF”,反过来,这个命题还成立吗?

追问1 是因为学生只给出了ΔABEΔCDF一种方法,其实还可以证ΔCEBΔAFD得到结论,从而在“一题多变”的基础上再体现“一题多解”. 追问2 主要是让学生明白,两条线段除了数量关系,还可以有位置关系. 追问3 为学学生呈现另外一种常见的变式方法: 交换条件和结论,同时考察学生对全等三角形的判定方法——两边和一角的理解.

“一题多解”遵循数学课程标准中提出的“经历从不同角度寻求分析问题和解决问题的方法的过程,体验解决问题方法的多样性”,“一题多变”引导学生再解决问题和处理问题的基础上,可以提出和发现问题,实现“两能”到“四能”的突破.

4 反思梳理 引航学生高阶思维的培育——谈一谈

本环节关键在于培养学生“颗粒归仓”的意识,教师对小结环节的精心设计和高度重视, 有利于学生实现“知识、技能、思想、经验”的自我建构.

在课堂小结环节,我给出如图9 的方式进行梳理、小结.

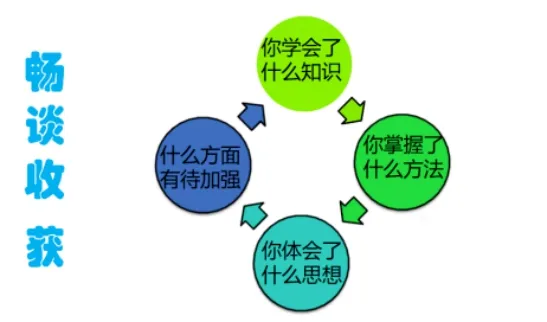
图9

课堂小结应在注重知识总结的同时,还应注重了研究问题的思路和相关思想的总结,做到既“授之鱼”,又“授之渔”.

总之, 良好的数学教学设计来自于“四个理解”, 教师只有深刻理解数学、理解学生、理解技术、理解教学的基础上, 才能整体设计出契合数学内在发展的逻辑与学生心理发展规律的课堂教学. 笔者这样处理,是基于对人教版教材的理解,基于对学生已有的认识、已有经验了解以及对“活动化教学”理解的基础上进行的教学设计. 采用“活动化教学”有利于学生在主动探究平行四边形的性质时,学会用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界,培养学生的数学抽象、直观想象、逻辑推理、数学建模等核心素养.